はじめに
前章でTight-bindingモデルを導出していく中で、原子軌道関数や局所ポテンシャルの積分で定義された重なり積分
\int\varphi_m^*(\boldsymbol{r}-\boldsymbol{R}) \varphi_l(\boldsymbol{r-\boldsymbol{R}'})d\boldsymbol{r} \simeq \delta_{m,n}\delta_{\boldsymbol{R},\boldsymbol{R}'}
や飛び移り積分
\int
\phi_n^*(\boldsymbol{r})
V(\boldsymbol{r} - \boldsymbol{R})
\phi_m(\boldsymbol{r}-\boldsymbol{R})d\boldsymbol{r}
\equiv
- t_{\boldsymbol{R}}^{n,m}
が定義され、それぞれ重なり積分は「小さな値」として近似されたり、飛び移り積分はバンドの形状に大きな影響を与えたり、Tight-bindingモデルの構築に当たり重要な役割を果たしていました。
それぞれの積分は、「何を計算すればよいか」は式を見れば明らかなのですが、じゃあ実際どのような物理的なイメージと対応しているのかと考え始めてみると分かりそうでよくわかりません(でした、私は)。
ググってみてもイマイチ自分が欲しい答えも見つかりません(ググり力が足りないだけかもしれません)。
というわけで、色々考えて自分なりに納得した内容について、本章で飛び移り積分について、次の章重なり積分について、書き残しておこうと思います。
間違った内容を書いてたりする可能性大なので注意してください。
特に、前章では(最)隣接格子間の飛び移り積分を考えましたが、本章では一旦は「隣接」しない全ての格子間での飛び移り積分について考えていくことにします。
例によって長くなったので初めに概要を書いておくと、本章では、まずは比較的(多分)まともなことが書けそうな飛び移り積分について、
ことから、「飛び移り積分」は「結晶の中のある格子点で孤立した原子軌道が、微小時間後に別の格子点、別の状態に「飛び移る」確率」に対応しているというようなことを妄想して考えていきます。
孤立原子軌道に対する飛び移り積分について
早速始めましょう。
「飛び移り積分」と名前がついている通り、格子点間の電子の移動に関係が深い積分であることが予測され、さらに少し先取りして書くと、第二量子化表示をした場合
\mathcal{H} = \sum_{\left <i,j \right>,\sigma }-t_{ij}
\left(a^\dagger_{i\sigma }a_{j\sigma } + h.c.\right)
のように書かれ、「サイトjの電子が、サイトiの電子に変わる」=飛び移っていくようなそんな式の係数になっていたりします。
というわけで何か電子の移動確率みたいなもんなのかな?という印象を強く受けるわけですが、具体的にどのような物理量や物理的現象に対応しているのか、分かるようでこれを見ただけではわかりません。「あるサイトの原子軌道と、隣のサイトの局所ポテンシャルと原子軌道との積を積分することはわかったけどそれでその値は、何を意味するの?」って感じです。
というわけで順を追って、飛び移り積分と物理的な現象?を結びつけていきたいと思います
原子軌道関数の従う方程式
まず初めに、前章と同じく固体のポテンシャルを1電子近似し、かつ局所ポテンシャルの和で近似した1電子ハミルトニアン
\hat{H}^{\rm c} = \frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}}V(\boldsymbol{r}-\boldsymbol{R})
を考えます(ハミルトニアンの添え字"c"はCrystalの"c"のつもり)。ここで、固体の3方向の基本併進ベクトルを\boldsymbol{a}_i, i=1,2,3、格子ベクトルを\boldsymbol{R} = \sum_in_i\boldsymbol{a}_i, n_i = 0,\pm 1,\pm 2\cdotsとして、\boldsymbol{a}_i方向にN_i\boldsymbol{a}_i進むと元に戻る周期的境界条件を考え、局所ポテンシャルの総和\sum_{\boldsymbol{R}}も周期的境界条件の1周期分(≒結晶全体)について和を取ります。
また、前章と同じように原点のポテンシャルだけ抜き出した孤立原子ハミルトニアン\hat{H}^{\rm a} = \frac{-\hbar^2}{2m}\nabla^2 + V(\boldsymbol{r})に対して、固有値(原子準位)\varepsilon_m^{\rm a}を持つ固有状態である原子軌道を\phi_m(\boldsymbol{r})と書きます。
ここである原子軌道\phi_mに、結晶のハミルトニアンをおもむろに掛けてみますと、
\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}}V(\boldsymbol{r}-\boldsymbol{R})
\right) \phi_m(\boldsymbol{r})
固有関数\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})がBloch和\Phi_{m,\boldsymbol{k}}(\boldsymbol{r}) = \sum_{\boldsymbol{R}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}} \phi_m(\boldsymbol{r} - \boldsymbol{R})で展開できたことから、原子軌道\phi_m(\boldsymbol{r})にハミルトニアンが作用した後の関数も、関数系\{\phi_m(\boldsymbol{r} - \boldsymbol{R})\}で
\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}}V(\boldsymbol{r}-\boldsymbol{R})
\right) \phi_m(\boldsymbol{r}) = \sum_{m',\boldsymbol{R}'}c_{m',\boldsymbol{R}'}^{m,\boldsymbol{0}}\phi_{m}(\boldsymbol{r} - \boldsymbol{R}')
と展開できます。ここで、係数c_{m',\boldsymbol{R}'}^{m,\boldsymbol{0}}の上側のラベルの「\boldsymbol{0}」は、「格子点の内原点と一致する点\boldsymbol{R}=\boldsymbol{0}を中心とする原子軌道の展開」であることを意味しています。
証明っぽい内容
突然原子軌道関数を格子点だけ平行移動させた関数が登場しましたが、本当にこの関数系で任意の関数を展開できるのでしょうか?
これは以下のように考えれば良さそうです:
まず、何度も見てきたように、結晶のハミルトニアン\hat{H}^{\rm c}の固有値\varepsilon_{n,\boldsymbol{k}}を持つ固有状態\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}):
\hat{H}^{\rm c} \varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) = \varepsilon_{n,\boldsymbol{k}}\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})
は、孤立原子ハミルトニアン\hat{H}^{\rm a} = \frac{-\hbar^2}{2m}\nabla^2 + V(\boldsymbol{r})に対して、固有値(原子準位)\varepsilon_m^{\rm a}を持つ固有状態である原子軌道\phi_m(\boldsymbol{r})からなるBloch和\Phi_{m,\boldsymbol{k}}(\boldsymbol{r}) = \sum_{\boldsymbol{R}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}} \phi_m(\boldsymbol{r} - \boldsymbol{R})で
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) =
\sum_m b_m^n\Phi_m(\boldsymbol{r}) ,\\
\Phi_{m,\boldsymbol{k}}(\boldsymbol{r}) = \sum_{\boldsymbol{R}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}} \phi_{m}(\boldsymbol{r} - \boldsymbol{R})
と展開できます。行列とベクトルで表現すると、
から行列Bを定義して、
\begin{bmatrix}
\varphi_{1,\boldsymbol{k}}(\boldsymbol{r}) \\
\varphi_{2,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots\\
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots
\end{bmatrix}
=
B
\begin{bmatrix}
\Phi_{1,\boldsymbol{k}}(\boldsymbol{r}) \\
\Phi_{2,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots\\
\Phi_{n,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots
\end{bmatrix}
のような変換を考えることができます。
一方この展開を逆に考えると、B^{-1}B = I(Iは単位行列)を満たす逆行列B^{-1}の要素を
(B^{-1})_{nm} \equiv \tilde{b}_{m}^{n}
と書くことにして、逆変換
\begin{bmatrix}
\Phi_{1,\boldsymbol{k}}(\boldsymbol{r}) \\
\Phi_{2,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots\\
\Phi_{n,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots
\end{bmatrix}
=
B^{-1}
\begin{bmatrix}
\varphi_{1,\boldsymbol{k}}(\boldsymbol{r}) \\
\varphi_{2,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots\\
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) \\
\vdots
\end{bmatrix}
を定義できます。
これらとBloch和の「逆変換」\phi_m(\boldsymbol{r}-\boldsymbol{R}) = N^{-1}\sum_{\boldsymbol{k}}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}\Phi_{m,\boldsymbol{k}}(\boldsymbol{r})を用いて、原子軌道関数を固有関数の線形結合で表す以下の関係式が得られます:
\phi_{m}(\boldsymbol{r}-\boldsymbol{R}) = \frac{1}{N}\sum_{n,\boldsymbol{k}}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}\tilde{b}_m^n\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}).
特に、\boldsymbol{R} = \boldsymbol{0}の関係式は以下の通りです:
\phi_{m}(\boldsymbol{r}) = \frac{1}{N}\sum_{n,\boldsymbol{k}}\tilde{b}_m^n\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}).
さて、この関係式を初めの式へ代入すると、\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})は\hat{H}^{\rm c}の固有関数なので、
\begin{align*}
\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}}V(\boldsymbol{r}-\boldsymbol{R})
\right) \phi_m(\boldsymbol{r})
&=
\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}}V(\boldsymbol{r}-\boldsymbol{R})
\right)
\frac{1}{N}\sum_{n,\boldsymbol{k}}\tilde{b}_m^n\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})
\\
&=
\frac{1}{N}\sum_{n,\boldsymbol{k}}\varepsilon_{n,\boldsymbol{k}}\tilde{b}_m^n\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})
\end{align*}
となりますが、さらに今度は\varphi_{n\boldsymbol{k}}を原子軌道関数(Bloch和)で展開して、
\begin{align*}
(上式右辺)&=
\frac{1}{N}\sum_{n,\boldsymbol{k}}\varepsilon_{n,\boldsymbol{k}}\tilde{b}_m^n\sum_{m'} b_{m'}^n\sum_{\boldsymbol{R}'}e^{i\boldsymbol{k}\cdot\boldsymbol{R}'} \phi_{m'}(\boldsymbol{r} - \boldsymbol{R}')
\end{align*}
さらにBloch波数の関数\varepsilon_{n,\boldsymbol{k}}のFourier展開(Bloch関数に加え、固有関数もBloch波数について逆格子ベクトルを周期とする周期関数なのでした。というわけで、Bloch関数と同様に、直接格子の格子ベクトルを用いてFourier展開できます)
\varepsilon_{n,\boldsymbol{k}} = \sum_{\boldsymbol{R}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}}\varepsilon_{n,\boldsymbol{R}},\\
\varepsilon_{n,\boldsymbol{R}} = \frac{1}{N}\sum_{\boldsymbol{k}}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}\varepsilon_{n,\boldsymbol{k}}
を代入して、
\begin{align*}
(上式右辺)&=
\frac{1}{N}\sum_{n,\boldsymbol{k}}\sum_{\boldsymbol{R}''}e^{i\boldsymbol{k}\cdot\boldsymbol{R''}}\varepsilon_{n,\boldsymbol{R}''}\tilde{b}_m^n\sum_{m'} b_{m'}^n\sum_{\boldsymbol{R}'}e^{i\boldsymbol{k}\cdot\boldsymbol{R}'} \phi_{m'}(\boldsymbol{r} - \boldsymbol{R}')
\end{align*}
となります。ここで\boldsymbol{k}の総和が計算できるので、\sum_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot(\boldsymbol{R}' + \boldsymbol{R}'')} = N\delta_{\boldsymbol{R}',-\boldsymbol{R}''}を用いて最終的に、
\begin{align*}
\hat{H}^{\rm c}\phi_m(\boldsymbol{r})&=
\sum_{m'}
\sum_{\boldsymbol{R}'}
\left(\sum_{n}\varepsilon_{n,-\boldsymbol{R}'}\tilde{b}_m^n b_{m'}^n
\right)\phi_{m'}(\boldsymbol{r} - \boldsymbol{R}')
\\
&\equiv
\sum_{m',\boldsymbol{R}'}c_{m',\boldsymbol{R}'}^{m,\boldsymbol{0}}\phi_{m'}(\boldsymbol{r}-\boldsymbol{R}').
\end{align*}
\varepsilon_{n,-\boldsymbol{R}'}の係数にマイナスがついていることが気になりますが、以上のように、係数の具体的な中身はともかく、「原子軌道関数に結晶のハミルトニアンを作用させた後の関数」が、関数系\{\phi_m(\boldsymbol{r}-\boldsymbol{R})\}で展開できることを示せました。
\varepsilon_{n,-\boldsymbol{R}'}を具体的に展開していくともう少し情報が得られるかもしれませんが、一旦考えるのをやめときます。
ここで、前章に引き続きTight-bindingな近似を取り入れ、異なる原子軌道間の重なり積分をゼロと置く:
\int\varphi_m^*(\boldsymbol{r}-\boldsymbol{R}) \varphi_l(\boldsymbol{r-\boldsymbol{R}'})d\boldsymbol{r} \simeq \delta_{m,n}\delta_{\boldsymbol{R},\boldsymbol{R}'}
と、\phi_{m'}(\boldsymbol{r} - \boldsymbol{R}')にかかる展開係数c_{m',\boldsymbol{R}'}^{m,\boldsymbol{0}}は、
c_{m',\boldsymbol{R}'}^{m,\boldsymbol{0}} = \int\phi^*_{m'}(\boldsymbol{r} - \boldsymbol{R}')\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}''}V(\boldsymbol{r}-\boldsymbol{R}'')
\right)\phi_m(\boldsymbol{r})d\boldsymbol{r}
となります。さらに、孤立原子ハミルトニアン部分の固有関数であることを利用して、今回は右側の原子軌道にハミルトニアンの孤立原子部分を作用させて固有値を抜き出し、
\begin{align*}
(上式右辺)&=
\varepsilon_m^{\rm a}\int\phi_{m'}^*(\boldsymbol{r} + \boldsymbol{R}')\phi_m(\boldsymbol{r})d \boldsymbol{r}
+
\int\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')
\left(
\sum_{\boldsymbol{R}'' \neq \boldsymbol{0}}V(\boldsymbol{r} - \boldsymbol{R}'')
\right)
\phi_m(\boldsymbol{r})d \boldsymbol{r} \\
&=
\varepsilon_m^{\rm a}\delta_{m,m'}\delta_{\boldsymbol{R}',\boldsymbol{0}}+
\int\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')
\left(
\sum_{\boldsymbol{R}'' \neq \boldsymbol{0}}V(\boldsymbol{r} - \boldsymbol{R}'')
\right)
\phi_m(\boldsymbol{r})d \boldsymbol{r}
\end{align*}
と書き換えることができます。ついに「飛び移り積分」っぽい形の積分がでてきましたね。
ここで\boldsymbol{R}' = \boldsymbol{0}とその他で分けると、
\boldsymbol{R}' = \boldsymbol{0}
\begin{align*}
c_{m',\boldsymbol{0}}^{m,\boldsymbol{0}} &\simeq
\varepsilon_m^{\rm a}\delta_{mm'}
+
\int\phi_{m'}^*(\boldsymbol{r})
\left(
\sum_{\boldsymbol{R}'' \neq \boldsymbol{0}}V(\boldsymbol{r} - \boldsymbol{R}'')
\right)
\phi_m(\boldsymbol{r})d \boldsymbol{r} \\
&=
\varepsilon_m^{\rm a}\delta_{mm'}
+\Delta\varepsilon_{m'm}
\end{align*}
と、原子準位\varepsilon_m^{\rm a}と結晶場積分\Delta\varepsilon_{m'm}で書けることがわかります。
\boldsymbol{R}' \neq \boldsymbol{0}
また\boldsymbol{R}' \neq \boldsymbol{0}の場合は、前章で行ったように「3中心積分」をゼロと置くと、
c_{m',\boldsymbol{R}'\neq \boldsymbol{0}}^{m,\boldsymbol{0}} \simeq
\int\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')
V(\boldsymbol{r}-\boldsymbol{R}')
\phi_m(\boldsymbol{r})d \boldsymbol{r}
を得ます。ここで積分\int\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')V(\boldsymbol{r}-\boldsymbol{R}')\phi_m(\boldsymbol{r})d \boldsymbol{r}は、前章で定義した(本章冒頭でも書いた)飛び移り積分の定義の複素共役:
\begin{align*}
\left(- t_{\boldsymbol{R}'}^{m,m'}\right)^* &=
\left(
\int
\phi_m^*(\boldsymbol{r})
V(\boldsymbol{r} - \boldsymbol{R}')
\phi_{m'}(\boldsymbol{r}-\boldsymbol{R}')d\boldsymbol{r}
\right)^*\\
&=
\int\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')
V(\boldsymbol{r}-\boldsymbol{R}')
\phi_m(\boldsymbol{r})d \boldsymbol{r}
\end{align*}
の形をしていることがわかります。複素共役になっちゃうのがやや違和感があるかもしれませんが、これは定義の問題で、教科書によってはこの形(複素共役の形)を「飛び移り積分」として定義しているものもあります。前章の定義はアシュクロフト・マーミンやグロッソ・パラビチニに従ったのですが、この後考える第二量子化では逆(複素共役の方で定義する)の方が都合が良さそうなので、この後は上記の方を「飛び移り積分」と書くことが多くなります。
話を戻して、係数c_{m',\boldsymbol{R}\neq \boldsymbol{0}}^{m,\boldsymbol{0}}は、「前の章で定義した飛び移り積分の複素共役」を用いて
\begin{align*}
c_{m',\boldsymbol{R}'\neq \boldsymbol{0}}^{m,\boldsymbol{0}}
=
\left(- t_{\boldsymbol{R}'}^{m,m'}\right)^* =
\int\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')
V(\boldsymbol{r}-\boldsymbol{R}')
\phi_m(\boldsymbol{r})d \boldsymbol{r}
\end{align*}
と書けることが分かりました。
以上より、\hat{H}^{\rm c}\phi_m(\boldsymbol{r}) =\sum_{m',\boldsymbol{R}'} c_{m',\boldsymbol{R}'}^{m,\boldsymbol{0}}\phi_{m'}(\boldsymbol{r}-\boldsymbol{R}')の展開係数は
c_{m',\boldsymbol{R}'}^{m,\boldsymbol{0}} \simeq
\left\{
\begin{array}{ll}
\varepsilon_m^{\rm a}\delta_{mm'} +\Delta\varepsilon_{m'm} & (\boldsymbol{R}' = \boldsymbol{0}) \\
-\left(t_{\boldsymbol{R}'}^{m,m'}\right)^* & (\boldsymbol{R}' \neq \boldsymbol{0})
\end{array}
\right.
となり、原子軌道関数に結晶のハミルトニアンを作用させた関係式は
\begin{align*}
\hat{H}^{\rm c} \phi_m(\boldsymbol{r})
&=
\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}''}V(\boldsymbol{r}-\boldsymbol{R}'')
\right) \phi_m(\boldsymbol{r}) \\
&\simeq
(\varepsilon_m^{\rm a} + \Delta\varepsilon_{mm})\phi_m(\boldsymbol{r})
+
\sum_{m'} \Delta\varepsilon_{m'm}\phi_{m'}(\boldsymbol{r})\\
&\>\>\>\>+\sum_{\boldsymbol{R}'}\sum_{m'}(-t_{\boldsymbol{R}'}^{m,m'})^*\phi_{m'}(\boldsymbol{r} - \boldsymbol{R}')
\end{align*}
となることが分かりました。
・・・だからどうしたという感じですが、ここで記憶の片隅から、波動関数にハミルトニアンを作用させた意味を引っ張り出してきます。
波動関数の時間発展
さて、定常状態ばっかり扱っていてもはや記憶の彼方に葬り去られていましたが、本来のシュレーディンガー方程式は時間と位置に関する微分方程式
i\hbar \frac{\partial}{\partial t}\psi(\boldsymbol{r},t) = \hat{H}\psi(\boldsymbol{r},t)
なのでした。さらに、時刻tから微小時間\Delta tの変化を考えると、左辺の偏微分を
\frac{\partial}{\partial t}\psi(\boldsymbol{r},t)\simeq
\frac{\psi(\boldsymbol{r},t + \Delta t) - \psi(\boldsymbol{r},t)}{\Delta t}
として、シュレーディンガー方程式の両辺をi\hbarで割って整理すると、微小時間についての波動関数の時間発展の式
\frac{\psi(\boldsymbol{r},t + \Delta t) - \psi(\boldsymbol{r},t)}{\Delta t}
\simeq
\frac{-i}{\hbar}\hat{H}\psi(\boldsymbol{r},t)\\
\Rightarrow
\psi(\boldsymbol{r},t + \Delta t) \simeq
\psi(\boldsymbol{r},t ) + \frac{-i}{\hbar}\Delta t\hat{H}\psi(\boldsymbol{r},t)
を得ることができます。これで準備が整ったので、結晶の中、t=0で原点に一つだけ孤立原子軌道がある場合の時間発展を考えてみましょう。すなわちハミルトニアン、t=0の波動関数を
\begin{align*}
&\hat{H} = \hat{H}^{\rm c}
=
\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}}V(\boldsymbol{r}-\boldsymbol{R})
\right),\\
&\psi(\boldsymbol{r},0) = \phi_m(\boldsymbol{r})
\end{align*}
の時間発展を考えます。これは先ほど得た関係式より、
\begin{align*}
\psi(\boldsymbol{r},\Delta t) &\simeq
\psi(\boldsymbol{r},0 ) + \frac{-i}{\hbar}\Delta t\hat{H}\psi(\boldsymbol{r},0)
\\
&\simeq
\phi_m(\boldsymbol{r})
+
\frac{-i}{\hbar}\Delta t\hat{H}\phi_m(\boldsymbol{r})
\\
&\simeq
\left\{1-\frac{-i}{\hbar}\Delta t
(\varepsilon_m^{\rm a} + \Delta\varepsilon_{mm})
\right\}
\phi_m(\boldsymbol{r})\\
&\>\>\>\>+
\frac{-i}{\hbar}\Delta t\sum_{m'} \Delta\varepsilon_{m'm}\phi_{m'}(\boldsymbol{r})\\
&\>\>\>\>+\frac{-i}{\hbar}\Delta t\sum_{\boldsymbol{R}'}\sum_{m'}\left(-t_{\boldsymbol{R}'}^{mm'}\right)^*\phi_{m'}(\boldsymbol{r} + \boldsymbol{R}')
\end{align*}
が得られます。すなわち、原点にポツンと1つ原子軌道があるとき、微小時間後の波動関数を各格子点に平行移動した、様々な準位の原子軌道\{\phi_{m'}(\boldsymbol{r} + \boldsymbol{R})\}の重ね合わせで書くことができました。この時の\phi_{m'}(\boldsymbol{r}+\boldsymbol{R})の係数はかなり雑に言うと「電子が格子点-\boldsymbol{R}上で、m'の原子軌道で存在する確率」つまり「原点の格子点\boldsymbol{R} = \boldsymbol{0}にいた状態mの電子が、格子点-\boldsymbol{R}に状態m'で「飛び移る」確率」と考えられそうです。
注意点1
ここで位置を表す変数が\boldsymbol{r}と、\boldsymbol{R}の二つ出てきて紛らわしいのですが、前者\boldsymbol{r}は「電子の波動関数の形」\simeq「電子の確率雲の形」に対応する変数で、後者\boldsymbol{R}は「波動関数の中心」\simeq「固体の中の電子の場所」に対応する変数です。この表現もかなり正確性がアヤシイですが。。。
注意点2
正確(?)には、波動関数は観測することができず、観測できるのはエルミート演算子で表される何かしらの物理量です。そして、ある波動関数を何らかの演算子の固有状態で展開していた時、物理量の測定を通してその固有状態である波動関数が確定します(なんかこの書き方もイマイチな気がする・・)。そこで、波動関数\phi_m(\boldsymbol{r}-\boldsymbol{R})は何か物理量に対応する演算子の固有状態になっているかというと、そこが良くわかっていないので、例えば上記のような時間発展を考えたとしても、時刻\Delta t後に、「電子が格子点\boldsymbol{R}上で、m'の原子軌道で存在する」かどうかを確認できるかというとそういうわけではないように思えます。
原子軌道の飛び移り積分の物理的意味
特に、微小時間\Delta t後に、電子が原点から格子ベクトル\boldsymbol{R}'で指定される格子点に局在した原子軌道\phi_{m'}(\boldsymbol{r}-\boldsymbol{R}')となっているような確率は、飛び移り積分(t_{\boldsymbol{R}'}^{m,m'})^*:
\begin{align*}
-\left(t_{\boldsymbol{R}'}^{m,m'}\right)^* &=
\left(
\int_V\phi_{m}^*(\boldsymbol{r})
V(\boldsymbol{r}-\boldsymbol{R}')
\phi_{m'}(\boldsymbol{r}-\boldsymbol{R}')d \boldsymbol{r}
\right)^*\\
&=
\int_V\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')
V(\boldsymbol{r}-\boldsymbol{R}')
\phi_m(\boldsymbol{r})d \boldsymbol{r}
\end{align*}
に比例(?)することがわかります。
以上のように(きわめて怪しい)議論を繰り広げることで、飛び移り積分 (の複素共役) はその名前の通り、原点(あるいはある格子点\boldsymbol{R})にいるm状態の原子軌道\phi_m(\boldsymbol{r})(\phi_m(\boldsymbol{r}-\boldsymbol{R}))が、(微小時間後に)状態m'になって原点(あるいはある格子点\boldsymbol{R})から格子ベクトル\boldsymbol{R}'離れた場所へ、\phi_{m'}(\boldsymbol{r}-\boldsymbol{R})(\phi_{m'}(\boldsymbol{r}-\boldsymbol{R}-\boldsymbol{R}'))として飛び移って行く確率(に比例(?)する量)を表すことが分かりました。
飛び移り積分が前後の格子点の相対ベクトルのみに依存する性質
最後に、(これを確かめるのには今回の議論は不要ですが)飛び移り積分は飛び移り前と後の格子ベクトルの 差(=飛び移り前の格子点から飛び移り先の格子点へ向かう相対ベクトル) のみに依存することを次のように確認できます。すなわち、格子点\boldsymbol{R}から格子点\boldsymbol{R}'への飛び移り積分
c_{m',\boldsymbol{R}'\neq \boldsymbol{R}}^{m,\boldsymbol{R}} \simeq
\int\phi_{m'}^*(\boldsymbol{r} - \boldsymbol{R}')
V(\boldsymbol{r}-\boldsymbol{R}')
\phi_m(\boldsymbol{r} - \boldsymbol{R})d \boldsymbol{r}
は、積分変数の変換\boldsymbol{r} - \boldsymbol{R}\rightarrow\boldsymbol{r}に対して、周期的境界条件より積分の値を変えないので、変数変換後の積分
\int\phi_{m'}^*(\boldsymbol{r} + \boldsymbol{R} - \boldsymbol{R}')
V(\boldsymbol{r} + \boldsymbol{R} -\boldsymbol{R}')
\phi_m(\boldsymbol{r})d \boldsymbol{r}
を考えて、飛び移り前の格子点\boldsymbol{R}から飛び移り後の格子点\boldsymbol{R}'へ向かう相対ベクトル\boldsymbol{R}' - \boldsymbol{R}により
c_{m',\boldsymbol{R}'\neq \boldsymbol{R}}^{m,\boldsymbol{R}} =
\int\phi_{m'}^*(\boldsymbol{r} - (\boldsymbol{R}' - \boldsymbol{R}))
V(\boldsymbol{r}-(\boldsymbol{R}' - \boldsymbol{R}))
\phi_m(\boldsymbol{r})d \boldsymbol{r}
であることもわかります。
以上をまとめると、飛び移り積分に関する次の物理的意味が分かりました。これでひとまず本章の目標は達成です。
なお、先ほどもちらっと述べましたが、後に使うには元々定義しておいた飛び移り積分の複素共役を改めて飛び移り積分と定義したほうが使いやすそうです。また、飛び移りの方向もややこしいので明示しておいた方が良さそうです。というわけで今後はこれらがわかりやすいように、
-t_{(m,\boldsymbol{R}+ \boldsymbol{R}') \leftarrow (n,\boldsymbol{R})}
\equiv
\int
\phi_m^*(\boldsymbol{r}-\boldsymbol{R}')
V(\boldsymbol{r} - \boldsymbol{R}')
\phi_n(\boldsymbol{r})d\boldsymbol{r}
のようにも書くと思います。
将来の自分への余談
今回の話の展開は、あえて最初に\boldsymbol{R} = 0の場合を取らず、一般の\boldsymbol{R}に局在する原子軌道の展開を扱っていれば、わざわざ話を二段階に分ける必要なく「飛び移り積分の意味」「複素共役の意味」を説明できたような気がする。
あと、そうすれば積分変数の変換\boldsymbol{r} - \boldsymbol{R} + \boldsymbol{R}' \rightarrow \boldsymbol{r} - \boldsymbol{R}''みたいなことを通して、飛び移り前と後の格子点の差分だけで書けるね、みたいな話の展開ができたような気がする。いつか書き直すときはそういう風にしよう
ダメ押しのイメージ
さて、これまで飛び移りが「飛び移る確率」に「比例(?)」すると書いてきましたが、よく考えれば波動関数を
\psi(\boldsymbol{r} )= \sum_i c_i \phi_i(\boldsymbol{r})
のように展開したとき、その波動関数が\phi_i(\boldsymbol{r})である確率(注:これは不正確な表現です)は、展開係数の絶対値の2乗|c_i|^2に比例するのでした。
なので、結局、「(\boldsymbol{R}_1,n)から(\boldsymbol{R}_1+\boldsymbol{R},m)に飛び移る確率」と、「(\boldsymbol{R}_2 + \boldsymbol{R},m)から(\boldsymbol{R}_1,n)に飛び移る確率」は、どちらも絶対値の2乗を考えれば等しいことがわかります。(繰り返しになりますが格子点\boldsymbol{R}を中心とする原子軌道\phi_m(\boldsymbol{r} - \boldsymbol{R})が固有状態となる物理量がよくわからない限り具体的にこの「飛び移り」を観測することはかなわないのですが)
そしてダメ押しで今まで見てきた内容をイラスト的にイメージしてみると、
時刻0で原点にいた状態mの原子軌道\phi_m(\boldsymbol{r})
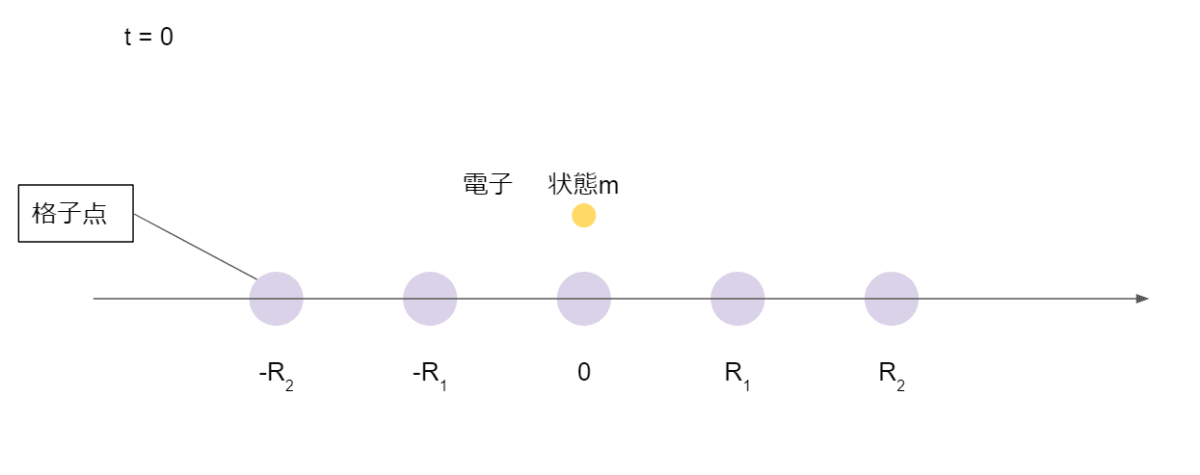
は、微小時間後に、
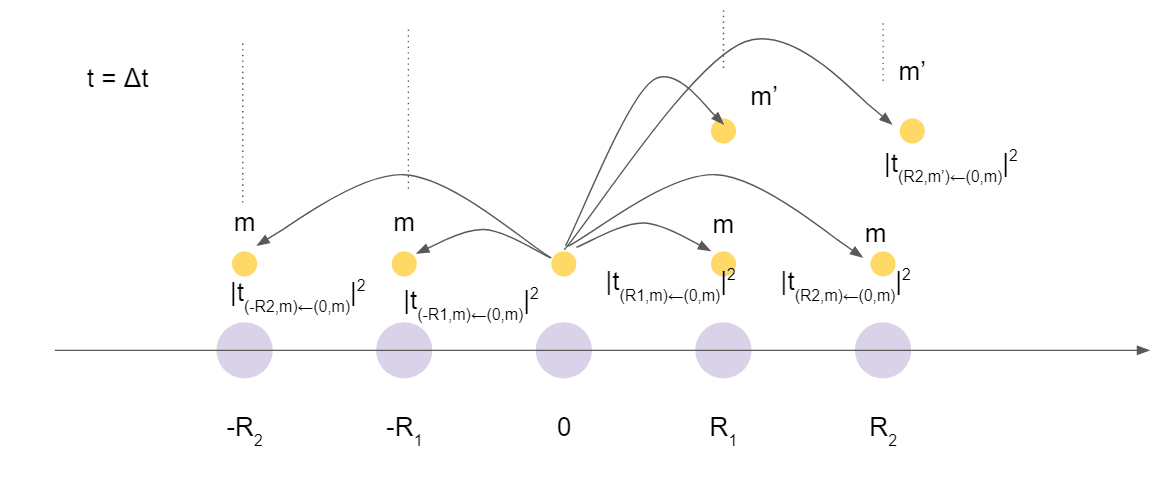
のように、様々な格子点へ、原子軌道を変化させながら飛び移り積分(の絶対値の2乗)に比例する確率で「飛び移って」行くようなイメージが描けました。
ただ、これがわかったところで、微小時間後の波動関数が測定できるわけでもないし、何の意味があるのかは分かりませんが。というか自己満足ですが。
(おまけ1)LCAO近似:少数の原子軌道での展開との関係
さて、ここからはおまけとして、前々章で行った「固体の固有関数をエネルギー的に近い少数の原子軌道関数で展開する」というLCAO近似と、飛び移り積分との関係について考えてみます。
前々章で導いた展開係数の関係式を見てみると、
\begin{align*}
(\varepsilon_{n,\boldsymbol{k}} - \varepsilon_l^{\rm a})b_l^n
&=
-(\varepsilon_{n,\boldsymbol{k}} - \varepsilon_l^{\rm a})
\sum_m
\left[
\sum_{\boldsymbol{R}\neq\boldsymbol{0}}
e^{i\boldsymbol{k}\cdot\boldsymbol{R}}
\int \phi_l^*(\boldsymbol{r})
\phi_m(\boldsymbol{r}-\boldsymbol{R})d\boldsymbol{r}
\right]b_m^n \\
&\>\>\>\>+
\sum_m
\left[
\int \phi_l^*(\boldsymbol{r})
\left(
\sum_{\boldsymbol{R}'\neq \boldsymbol{0}}
V(\boldsymbol{r}-\boldsymbol{R}')
\right) \phi_m(\boldsymbol{r})d\boldsymbol{r}
\right] b_m^n\\
&\>\>\>\>+
\sum_m
\left[
\sum_{\boldsymbol{R}\neq\boldsymbol{0}}
e^{i\boldsymbol{k}\cdot\boldsymbol{R}} \int \phi_l^*(\boldsymbol{r})
\left(
\sum_{\boldsymbol{R}'\neq \boldsymbol{0}}
V(\boldsymbol{r}-\boldsymbol{R}')
\right) \phi_m(\boldsymbol{r}-\boldsymbol{R})d\boldsymbol{r}
\right]b_m^n
\end{align*}
これが\varepsilon_{n,\boldsymbol{k}} \ll \varepsilon_L^{\rm a}の時b_L^n\simeq 0としたのでした。異なる軌道間の重なり積分がゼロとすれば、残るは異なる軌道間の結晶場積分と、飛び移り積分です。
そしてこれらをゼロと置く近似が、結局のところ「固有関数を少数のエネルギー的に近い原子軌道で展開できる」という近似に対応しているわけでした。
さて、今までスルーしましたが、結晶場積分は「局在する格子点の位置は変えずに、原子準位だけが変わる」確率に対応していそうです。また、飛び移り積分はこれまで見てきたように異なる格子点へ、異なる準位になって飛び移る確率に対応しています。
ここで、エネルギー的に離れた準位l,Lを考えた場合、その間の飛び移り積分
t_{(L,\boldsymbol{R}+\boldsymbol{R}')\leftarrow (l,\boldsymbol{R})}
は、「格子ベクトル\boldsymbol{R}'離れた位置に、(突然)高エネルギーになって飛び移る確率」に対応しており、先ほどのイメージと比べてもこれを無視することは、妥当な近似であろうことが納得されます。
また、隣接格子間のみの飛び移り積分を残す近似も、今回考えた展開
\begin{align*}
\hat{H}^{\rm c} \phi_m(\boldsymbol{r})
&=
\left(
\frac{-\hbar^2}{2m}\nabla^2 + \sum_{\boldsymbol{R}''}V(\boldsymbol{r}-\boldsymbol{R}'')
\right) \phi_m(\boldsymbol{r}) \\
&\simeq
(\varepsilon_m^{\rm a} + \Delta\varepsilon_{mm})\phi_m(\boldsymbol{r})
+
\sum_{m'} \Delta\varepsilon_{m'm}\phi_{m'}(\boldsymbol{r})\\
&\>\>\>\>+\sum_{\boldsymbol{R}'}\sum_{m'}(-t_{\boldsymbol{R}'}^{m,m'})^*\phi_{m'}(\boldsymbol{r} - \boldsymbol{R}')
\end{align*}
の2式目第3項について、隣接格子へ飛び移る過程のみを取り入れる近似だとわかります。(二つの格子点が離れれば離れるほど、飛び移る確率は当然低くなるでしょうから、これも納得の近似です。)
なお、蛇足ですが、前章で見たようにこれとエネルギー的に離れた軌道間の重なり積分をゼロと置けば固有値方程式はブロック対角化されますが、その後エネルギー的に近い軌道間の重なり積分はゼロと置かずとも、グループqの一般化固有値方程式(各記号の定義はTight-bindingモデル(前編)
(後編)等を参照していただくとして省略
\begin{vmatrix}
M_{\boldsymbol{k}}^q - \varepsilon_{\boldsymbol{k}} S_{\boldsymbol{k}}^q
\end{vmatrix} = 0
の重なり行列S_{\boldsymbol{k}}^qを対角化して、対角化行列によるユニタリ変換で得られる原子軌道の重ね合わせを新たな「原子軌道」とすれば、これらは行列の異なる固有値に属するので自動的に異なる「原子軌道」間の重なり積分はゼロとなります。つまりエネルギー的に近い軌道の重なり積分はゼロと近似しなくても、その上手い線形結合の間の飛び移り積分と展開係数を一致させることができ、より良い近似が得られると期待されます。
なお(2回目)、前章でグダグダ書いた、「とはいえ、エネルギーの高い軌道が空間的には広がっているはずだから、積分は大きくなりそうじゃない?」という疑問について、ダメ押しで追記しておくと、確かにエネルギーが高い軌道は広がっていますが、同時に激しく振動している(電子がではなく、関数の形が)と考えられ、(激しく振動する関数)×(穏やかに変化する関数)の積を積分すると、振動部分が打ち消しあって「重なり」は大きくても積分結果は小さくなる、と考えることもできそうです。
(おまけ2)Wannier関数の従うべき方程式と時間発展
最後に、 これも何の役に立つのかわかりませんが、 局在基底であるWannier関数の関係式と、時間発展についておまけで触れておきます。
先ほどと同様に固体のポテンシャルを1電子近似した1電子ハミルトニアン
\hat{H}^{\rm c} = \frac{-\hbar^2}{2m}\nabla^2 + U(\boldsymbol{r})
を考えます。ここでU(\boldsymbol{r})は、固体の3方向の基本併進ベクトルを\boldsymbol{a}_i, i=1,2,3、格子ベクトルを\boldsymbol{R} = \sum_in_i\boldsymbol{a}_i, n_i = 0,\pm 1,\pm 2\cdotsとしてU(\boldsymbol{r} + \boldsymbol{R}) =U(\boldsymbol{r})を満たす周期ポテンシャルです。
何度も見てきたように、このハミルトニアンの固有値\varepsilon_{n,\boldsymbol{k}}を持つ固有状態\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}):
\hat{H}^{\rm c} \varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) = \varepsilon_{n,\boldsymbol{k}}\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})
は、局在関数Wannier関数w_{n,\boldsymbol{R}}(\boldsymbol{r})=w_n(\boldsymbol{r}-\boldsymbol{R})で
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r}) =\sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}},\\
w_{n,\boldsymbol{R}}(\boldsymbol{r})
=
\frac{1}{N}\sum_{\boldsymbol{k}} \varphi_n(\boldsymbol{r},\boldsymbol{k})e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}
と展開できます。このWannier関数の展開を1体シュレーディンガー方程式に代入すると、固体の1電子ハミルトニアンに対するWannier関数の満たす関係式
\hat{H}^{\rm c}w_{n,\boldsymbol{R}} = \sum_{\boldsymbol{R}'}\varepsilon_{n,\boldsymbol{R} - \boldsymbol{R}'}w_{n,\boldsymbol{R}'}
を導くことができます。ここで\varepsilon_{n,\boldsymbol{R}}は、Bloch波数の関数\varepsilon_{n,\boldsymbol{k}}のFourier展開
\varepsilon_{n,\boldsymbol{k}} = \sum_{\boldsymbol{R}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}}\varepsilon_{n,\boldsymbol{R}},\\
\varepsilon_{n,\boldsymbol{R}} = \frac{1}{N}\sum_{\boldsymbol{k}}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}\varepsilon_{n,\boldsymbol{k}}
です。
Wannier関数の正規直交性\int_V w_{n'}^*(\boldsymbol{r}-\boldsymbol{R}')w_n(\boldsymbol{r} - \boldsymbol{R})dr =\delta_{n,n'}\delta_{\boldsymbol{R},\boldsymbol{R}'}から、\varepsilon_{n,\boldsymbol{R}-\boldsymbol{R}'} = \int w_{n,\boldsymbol{R}'}^*(\boldsymbol{r})\hat{H}^{\rm c}w_{n,\boldsymbol{R}}(\boldsymbol{r})d\boldsymbol{r}です。これはBloch関数が満たすシュレーディンガー方程式に\varepsilon_{n,\boldsymbol{k}} = \sum_{\boldsymbol{R}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}}\varepsilon_{n,\boldsymbol{R}}を代入してe^{-i\boldsymbol{k}\cdot\boldsymbol{R}'}をかけて積分しても示すことができます
証明
まずWannier関数での展開をブロッホ関数が満たすシュレーディンガー方程式に代入する:
\hat{H}^{\rm c} \sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}}= \varepsilon_{n,\boldsymbol{k}}\sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}}.
次に固有値\varepsilon_{n,\boldsymbol{k}}について、これもBloch波数\boldsymbol{k}と逆格子ベクトル\boldsymbol{K}に関して、\varepsilon_{n,\boldsymbol{k} + \boldsymbol{K}} = \varepsilon_{n,\boldsymbol{k}}の周期性より、Bloch関数と同様に「逆格子ベクトルの逆格子ベクトル」格子ベクトル\boldsymbol{R}を用いてFourier展開できる:
\varepsilon_{n,\boldsymbol{k}} = \sum_{\boldsymbol{R}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}}\varepsilon_{n,\boldsymbol{R}},\\
\varepsilon_{n,\boldsymbol{R}} = \frac{1}{N}\sum_{\boldsymbol{k}}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}}\varepsilon_{n,\boldsymbol{k}}
ので、それもシュレーディンガー方程式に代入する:
\hat{H}^{\rm c} \sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}}
=
\sum_{\boldsymbol{R}'}e^{i\boldsymbol{k}\cdot\boldsymbol{R}'}\varepsilon_{n,\boldsymbol{R}'}
\sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{R}}.
両辺にe^{-i\boldsymbol{k}\cdot\boldsymbol{R}''}をかけて\boldsymbol{k}についてBZ内での積分(和)を取ると、N^{-1}\sum_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot(\boldsymbol{R} - \boldsymbol{R}'')} = \delta_{\boldsymbol{R},\boldsymbol{R}''}より、
\begin{align*}
(左辺)&=
\hat{H}^{\rm c} \sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})N^{-1}\sum_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot(\boldsymbol{R} - \boldsymbol{R}'')}\\
&=
\hat{H}^{\rm c} \sum_{\boldsymbol{R}}w_{n,\boldsymbol{R}}(\boldsymbol{r})\delta_{\boldsymbol{R},\boldsymbol{R}''}\\
&=
\hat{H}^{\rm c} w_{n,\boldsymbol{R}''}(\boldsymbol{r}).
\end{align*}
\begin{align*}
(右辺)&=
\sum_{\boldsymbol{R}'} \sum_{\boldsymbol{R}}\varepsilon_{n,\boldsymbol{R}'}
w_{n,\boldsymbol{R}}(\boldsymbol{r})
N^{-1}\sum_{\boldsymbol{k}}e^{i\boldsymbol{k}\cdot(\boldsymbol{R} + \boldsymbol{R}' - \boldsymbol{R}'')}\\
&=
\sum_{\boldsymbol{R}'} \sum_{\boldsymbol{R}}\varepsilon_{n,\boldsymbol{R}'}
w_{n,\boldsymbol{R}}(\boldsymbol{r})
\delta_{\boldsymbol{R}',\boldsymbol{R}''-\boldsymbol{R}}\\
&=
\sum_{\boldsymbol{R}}\varepsilon_{n,\boldsymbol{R}''-\boldsymbol{R}}
w_{n,\boldsymbol{R}}(\boldsymbol{r}).
\end{align*}
ここで記号を整えるために左辺、右辺ともに\boldsymbol{R}'' \rightarrow \boldsymbol{R}、\boldsymbol{R} \rightarrow \boldsymbol{R}'と置きなおすと、等式
\hat{H}^{\rm c} w_{n,\boldsymbol{R}}(\boldsymbol{r})
=
\sum_{\boldsymbol{R}'}\varepsilon_{n,\boldsymbol{R}-\boldsymbol{R}'}
w_{n,\boldsymbol{R}'}(\boldsymbol{r})
が得られる。
Wannier関数の時間発展
原子軌道の場合と同様にt=0で原点に局在したWannier関数の時間発展を考えると、\psi(\boldsymbol{r},0 ) =w_n(\boldsymbol{r})として、
\begin{align*}
\psi(\boldsymbol{r},\Delta t) &\simeq
\psi(\boldsymbol{r},0 ) + \frac{-i}{\hbar}\Delta t\hat{H}\psi(\boldsymbol{r},0)
\\
&=
w_n(\boldsymbol{r})
+
\frac{-i}{\hbar}\Delta t\hat{H}w_n(\boldsymbol{r})
\\
&=
w_n(\boldsymbol{r})
+
\frac{-i}{\hbar}\Delta t\sum_{\boldsymbol{R}'}\varepsilon_{n,\boldsymbol{R} - \boldsymbol{R}'}
w_{n,\boldsymbol{R}'}(\boldsymbol{r})\\
\end{align*}
となります。ここに\Delta tの時間発展を繰り返し考えていっても、どこまで行ってもWannier関数の関数形はそのままで、各格子点にいる確率だけが変わっていくと考えられます。
従って、結晶のポテンシャルの中で局在した一つのWannier関数は、形を変えることなく格子点を「飛び移って」行くことがわかります。
これも結局、格子点\boldsymbol{R}に局在したWannier関数が固有状態となる何かの物理量が無ければ、測定と結びつけることができないので本当に(?)物理的な理解とも言い難い気もするのですが、なんとなくのイメージとして面白いので書いておきました。
(逆にWannier関数が固有状態となる(エルミート)演算子=物理量を上手く構成できれば、上のような飛び移りが実際に観測できて面白そうですが、私には何も分かりません)
おわりに
以上のようにして飛び移り積分や原子軌道の振る舞いについて親しみを深められたところで、本章を終わりにします。
本章を通して、原子軌道関数に結晶のハミルトニアンを作用させた場合の展開
\begin{align*}
\hat{H}^{\rm c}\phi_m(\boldsymbol{r} - \boldsymbol{R})&=
\sum_{m'}
\sum_{\boldsymbol{R}'}
\left(\sum_{n}\varepsilon_{n,\boldsymbol{R}-\boldsymbol{R}'}\tilde{b}_m^n b_{m'}^n
\right)\phi_{m'}(\boldsymbol{r} - \boldsymbol{R}')
\\
&\equiv
\sum_{m',\boldsymbol{R}'}c_{m',\boldsymbol{R}'}^{m,\boldsymbol{R}}\phi_{m'}(\boldsymbol{r}-\boldsymbol{R}').
\end{align*}
と、波動関数の時間発展
\begin{align*}
\psi(\boldsymbol{r},\Delta t) &\simeq
\psi(\boldsymbol{r},0 ) + \frac{-i}{\hbar}\Delta t\hat{H}\psi(\boldsymbol{r},0)
\\
&\simeq
\phi_m(\boldsymbol{r})
+
\frac{-i}{\hbar}\Delta t\hat{H}\phi_m(\boldsymbol{r})
\\
&\simeq
\left\{1-\frac{-i}{\hbar}\Delta t
(\varepsilon_m^{\rm a} + \Delta\varepsilon_{mm})
\right\}
\phi_m(\boldsymbol{r})\\
&\>\>\>\>+
\frac{-i}{\hbar}\Delta t\sum_{m'} \Delta\varepsilon_{m'm}\phi_{m'}(\boldsymbol{r})\\
&\>\>\>\>+\frac{-i}{\hbar}\Delta t\sum_{\boldsymbol{R}'}\sum_{m'}\left(-t_{\boldsymbol{R}'}^{mm'}\right)^*\phi_{m'}(\boldsymbol{r} + \boldsymbol{R}')
\end{align*}
を考えることにより、突然定義された意味深な積分「飛び移り積分」について、具体的な「飛び移り」のイメージと結びつけることができました。
また同時に(副産物として)飛び移り積分の複素共役を取ると、「飛び移り方向」が逆になることを見ました。
以上まとめると以下のようになります。
つまり、時刻0で原点にいた状態mの原子軌道\phi_m(\boldsymbol{r})

は、微小時間後に、

のように、様々な格子点へ、原子軌道を変化させながら飛び移り積分(の絶対値の2乗)に比例する確率で「飛び移って」行くようなイメージが描けました。




Discussion