はじめに
前章で結晶の周期を持つ関数のFourier展開を定義することができたので、いよいよ固体、つまり周期的ポテンシャル内の電子の性質を考えていきます。
本稿のゴールであるTight-bindingモデルでは、格子点に孤立原子のポテンシャルが周期的に存在していると考えますが、本章ではより一般的に、ハミルトニアンが結晶の周期性を持つ場合にその固有状態が持つべき性質について整理します。
固体中の電子
固体内の電子のシュレーディンガー方程式
以前の章でも記載した通り、固体内の状態を色々と簡略化して考えると、原子核や内殻電子から受けるポテンシャルを全部まとめて1電子ポテンシャルに近似し、価電子間の相互作用を(一旦)無視することで、周期的に並んだ有効1電子ポテンシャルのもとを運動する相互作用しない多数の電子の状態を考えることになります。(下図も再掲しておきます)
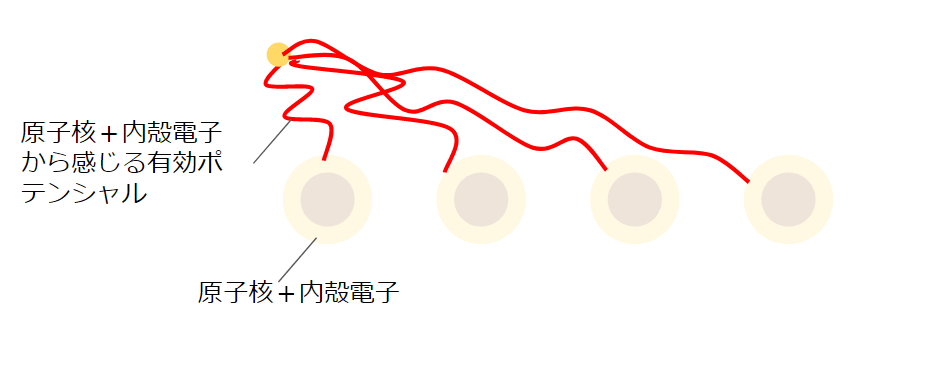
多体のハミルトニアンは、位置\boldsymbol{R}の原子核+内殻電子から、i番目の電子への有効ポテンシャルをV_i(\boldsymbol{r}_i-\boldsymbol{R})として、
\mathcal{H}\Phi(\boldsymbol{r}_1, \boldsymbol{r}_2,\cdots) = E\Phi(\boldsymbol{r}_1, \boldsymbol{r}_2,\cdots),\\
\mathcal{H} = \sum_i\left( -\frac{\hbar^2}{2m}\nabla_i^2\right) + \sum_i\sum_{\boldsymbol{R}}V_i(\boldsymbol{r}_i-\boldsymbol{R})
となります。
ここから変数分離をして、実際に扱うのは1電子シュレーディンガー方程式
\left\{
-\frac{\hbar^2}{2m}\nabla_i^2
+
\sum_{\boldsymbol{R}}V_i(\boldsymbol{r}_i-\boldsymbol{R})
\right\}
\varphi(\boldsymbol{r}) = \varepsilon\varphi(\boldsymbol{r})
へと帰着されます。そこから求めた一体の固有関数をエネルギーが低い順からスレーター行列式に詰めて行けば基底状態の波動関数を得ることができます。
しかし1電子のシュレーディンガー方程式になったところで、やはり上式はそのままでは解けません。具体的な解を求めるためにはさらなる近似が必要となります。
近似にも色々ありますが、そのうちの一つに多電子原子の章で活用した変分法、すなわち波動関数の解になりそうな試行関数を仮定し、仮定した関数が解となるための条件を考えていく方法があります。
多電子原子について変分法を考えた際は、水素原子のシュレーディンガー方程式(中心力ポテンシャルの下でのシュレーディンガー方程式)が厳密に解けていたこともあり、その波動関数を出発点に置き、それなりに上手くいくことを見ました。それでは今回のような周期的なポテンシャルのもとでの試行関数はどのようなものを選べば良いでしょうか。
ブロッホの定理
その指針となるのが、表題のブロッホの定理です。また、変分法の出発点にとどまらず、周期的なポテンシャルの下で電子がどのような性質を持つのか。あるいはその性質をどのような表現で考えて行けばよいのかなど、固体内の電子状態について考える際に前提となる情報を得ることができます。
というわけで本章では「周期的なポテンシャル中の1電子状態」に着目して、色々と考えていきます。
さて、話を戻して、今回考えるのは先ほど示したハミルトニアンよりももう少し一般的な状況、すなわち格子ベクトルの並進に対して周期的なハミルトニアンの下で波動関数が従うべき条件についての定理です。
そのようなポテンシャルをU(\boldsymbol{r})と置きます。U(\boldsymbol{r})は前章・前々章で定義した格子ベクトル
\boldsymbol{n} = n_1\boldsymbol{a}_1 + n_2\boldsymbol{a}_2 + n_3\boldsymbol{a}_3
に対して
U(\boldsymbol{r} + \boldsymbol{n}) = U(\boldsymbol{r})
を満たします。また微分演算子\nablaは、座標の並進に対して不変です。
初めに結論から書くと、この時、シュレーディンガー方程式
\hat{H}\varphi(\boldsymbol{r}) = \varepsilon\varphi(\boldsymbol{r}),\\
\hat{H} =
-\frac{\hbar^2}{2m}\nabla^2
+
U(\boldsymbol{r})
を満たす波動関数は以下の条件を満たす、というのがブロッホの定理です。
また、上記のブロッホの定理で導かれた固有値を考えることで、固体内の電子が持つエネルギーの性質を表すエネルギーバンドという概念が登場することになります。
本章ではそのあたりの内容について整理していきます。
以下、上記定理の証明や具体的な内容を書いていきます。
証明には並進の演算子を用いる方法と、波動関数が満たす条件を具体的に求める方法の2パターンあり、本章では後者の方針で証明を記載します。(前者の方がすっきりと書けるのですがその前提となる定理を色々と追記する必要があり、地道に理解できる後者の方向で書いていきます)
まずは「ブロッホ波数」とかいうものについては置いておいて、周期的なハミルトニアンの固有関数が格子ベクトル\boldsymbol{n}の並進(1次元の場合は定数naの並進)に対して
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r} + \boldsymbol{n}) = e^{i\boldsymbol{k}\cdot\boldsymbol{n}}
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})
または、結晶の周期性を持つ関数u_{n,\boldsymbol{k}}(\boldsymbol{r} + \boldsymbol{n}) = u_{n,\boldsymbol{k}}(\boldsymbol{r})を用いて
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})= e^{i\boldsymbol{k}\cdot\boldsymbol{r}}u_{n,\boldsymbol{k}}(\boldsymbol{r})
を満たすことを確かめていきます。
ブロッホの定理の前半部分の証明(1次元)
初めに、色々と考えやすくなるので1次元の場合について考えます。3次元の場合も後に触れますが、ほぼ同じです。
波数表示でのシュレーディンガー方程式
1次元版を考えるにあたり、1次元周期ポテンシャルの下でのシュレーディンガー方程式は以下のように書けます。
\left(
\frac{-\hbar^2}{2m}\frac{d^2}{d x^2} + U(x)
\right)
\varphi(x) = \varepsilon\varphi(x)
格子間隔(格子定数)をa、nを整数として、ポテンシャルは周期性
を満たします。
ここで境界条件として、十分大きな数Nを用いて
\varphi(x + Na) = \varphi(x)
を考えます。
この時、ポテンシャルU(x)は
U(x) = \sum_K U_K e^{iKx},\\
K = \frac{2\pi}{a}m, \>\>m = 0,\pm 1, \pm 2\cdots
とFourier展開できます。ここで波数Kは逆格子に対応するものなので、その意味を強調するために大文字で書いています。
また、周期的境界条件を設定したことから波動関数も周期Naを持ち、
\varphi(x) = \frac{1}{\sqrt{Na}}\sum_q c_q e^{iqx},\\
q = \frac{2\pi}{Na}m, \>\>m = 0,\pm 1, \pm 2\cdots
と展開できます。ここで係数1/\sqrt{Na}は上記周期的境界条件の下で波動関数を規格化するための係数です。
これらをシュレーディンガー方程式に代入して整理します。運動エネルギー項に対しては
\frac{d^2}{d x^2}\sum_{q}c_{q}e^{iqx}
=
\sum_{q}q^2c_{q}e^{iqx}
となります。またポテンシャル項について、
\begin{align*}
U(x)\varphi(x)
&=
\frac{1}{\sqrt{Na}}
\sum_{K}\sum_{q}U_{K}
c_{q}
e^{i(K+q)x}\\
&=
\frac{1}{\sqrt{Na}}\sum_{K}\sum_{q'}U_{K}
c_{q'-K}
e^{iq'x}\\
\end{align*}
ですが、q + K = \frac{2\pi}{Na}(m + Nm')\rightarrow q'の置き換えに対しても\sum_{q'}の和の範囲は変わらないので、改めてq'\rightarrow qと置きなおして、
U(x)\varphi(x)
=
\frac{1}{\sqrt{Na}}\sum_{K}\sum_{q}U_{K}
c_{q-K}
e^{iqx}\\
と書けます。これらをまとめて、波数表示のシュレーディンガー方程式を
\frac{1}{\sqrt{Na}}
\sum_{q}e^{iqx}
\left[
(\frac{\hbar^2}{2m}q^2 - \varepsilon)c_{q} +
\sum_{K}U_{K}
c_{q-K}
\right]
=0
と書き換えることができ、Fourier係数c_{q}の満たす方程式
(\frac{\hbar^2}{2m}q^2 - \varepsilon)c_{q} +
\sum_{K}U_{K}
c_{q-K} = 0
を得ることができます。
ブロッホ関数の導出
この方程式は任意に選んだあるqと、その逆格子分異なるq-K, q\pm K', q\pm K''の係数を持つFourier係数のみを含む(無限個の)連立方程式のブロックになっています。(このようなブロックを代表するqは、逆格子の周期に関して最小単位となる逆格子空間の単位胞内でとればよいことを後に確かめます)
行列表示の都合上、逆格子K=\frac{2\pi}{a}mは、m=0,\pm 1, \pm 2\cdotsなので、それぞれK_0(=0), \pm K_1, \cdots,\pm K_m\cdotsと書くと、あるqを選ぶと、その逆格子分だけ異なる係数に関する行列の固有値方程式
\begin{bmatrix}
\ddots & & & & \\
& \ddots & \\
& & \ddots & & &\\
& & & \\
\cdots & \cdots & U_{-K_2} & U_{-K_1} & \frac{\hbar^2}{2m}q^2 + U_0 & U_{K_1} & U_{K_2}&\cdots \\
\\
& & &&& \ddots & \\
&& & & &&\ddots & \\
&&& & & &&\ddots & \\
\end{bmatrix}
\begin{bmatrix}
\vdots \\
c_{q - K_m} \\
\vdots \\
c_q \\
\vdots \\
c_{q + K_m} \\
\vdots
\end{bmatrix}
= \varepsilon
\begin{bmatrix}
\vdots \\
c_{q - K_m} \\
\vdots \\
c_q \\
\vdots \\
c_{q + K_m} \\
\vdots
\end{bmatrix}
がブロックで抜き出されることになります。この方程式は行列H_qを
H_q = \begin{bmatrix}
\ddots & & & & \\
& \ddots & \\
& & \ddots & & &\\
& & & \ddots \\
\cdots & \cdots & U_{-K_2} & U_{-K_1} & \frac{\hbar^2}{2m}q^2 + U_0 & U_{K_1} & U_{K_2}&\cdots \\
\\
& & &&& \ddots & \\
&& & & &&\ddots & \\
&&& & & &&\ddots & \\
\end{bmatrix}
として固有値方程式
より無限個の固有値\varepsilon_{n,q}を求めれば、その固有値に対応した固有ベクトル
H_q
\begin{bmatrix}
\vdots \\
c_{n, q - K_m} \\
\vdots \\
c_{n,q} \\
\vdots \\
c_{n, q + K_m} \\
\vdots
\end{bmatrix}
=
\varepsilon_{n,q}
\begin{bmatrix}
\vdots \\
c_{n, q - K_m} \\
\vdots \\
c_{n,q} \\
\vdots \\
c_{n, q + K_m} \\
\vdots
\end{bmatrix}
を得ることができます。
ここで、\varepsilon_{n,q}はエネルギーが小さい順にラベルnを付与していくものとします。(そのように考えておくと後々都合が良くなります。)
この結果から、元々求めたかったシュレーディンガー方程式に対する固有関数を先ほど求めた固有ベクトルの係数\{c_{n,q-Km}\}を用いて
\varphi_{n,q}(x) = \frac{1}{\sqrt{Na}} \sum_{m}c_{n,q-K_m}e^{i(q-K_m)x}
を得ます。
すなわち、周期的なハミルトニアンに対する固有関数は、ある波数qと、全ての逆格子\cdots, K_{m-1}, K_m, K_{m+1}, \cdots分だけ異なる波数\cdots, q-K_{m-1},q- K_m,q- K_{m+1}, \cdotsの係数\cdots , c_{n, q-K_{m-1}}, c_{n,q-K_m}, c_{n, q-k_{m+1}}\cdotsのみをFourier成分として持つ関数として表される、ということがわかります。
実際、\varphi_{n,q}は\hat{H} = \frac{-\hbar^2}{2m}\frac{d^2}{d x^2} + U(x)に対して
\begin{align*}
\hat{H}\sum_m c_{n,q-K_m}e^{i(q-K_m)x}
&=
\sum_m\frac{\hbar^2}{2m}(q-K_m)^2c_{n,q-K_m}e^{i(q-K_m)x} + \sum_m \sum_{m'} U_{K_{m'}}c_{n,q-K_m}e^{i(q-(K_m - K_{m'}))x}\\
&=
\sum_m\frac{\hbar^2}{2m}(q-K_m)^2c_{n,q-K_m}e^{i(q-K_m)x} + \sum_{K_{m''}} \sum_{K_{m'}} U_{K_{m'}}c_{n,q-K_{m''}-K_{m'}}e^{i(q- K_{m''})x}\\
&=
\sum_m\frac{\hbar^2}{2m}(q-K_m)^2c_{n,q-K_m}e^{i(q-K_m)x} + \sum_{K_m} \sum_{K_{m'}} U_{K_{m'}}c_{n,q-K_m-K_{m'}}e^{i(q- K_m)x}\\
&=
\sum_m e^{i(q-K_m)x} \left[
\frac{\hbar^2}{2m}(q-K_m)^2c_{n,q-K_m} + \sum_{m'} U_{K_{m'}}c_{n,q-K_m-K_{m'}}
\right]
\\
&=
\sum_m e^{i(q-K_m)x} \left[
\sum_l(H_q)_{m,l}
c_{n,q-K_l}
\right]\\
&=
\sum_m e^{i(q-K_m)x} \left[
\varepsilon_{n,q}
c_{n,q-K_m}
\right]
\end{align*}
と、固有状態になっていることがわかります。
またラベルmについての和は、逆格子Kについての和と等しいので、エネルギー固有値\varepsilon_{n,q}に対応する固有関数は
\varphi_{n,q}(x) = \frac{1}{\sqrt{Na}}\sum_K c_{n,q-K}e^{i(q-K)x}
とも書けます。
ブロッホ関数の座標並進に対する性質(ブロッホの定理の前半の証明)
さて、当初目標のブロッホの定理の前半部分ですが、これは実際に代入してみれば確かめることができます。
この関数は格子の並進x\rightarrow x + naに対して、e^{iKna} = 1より、
\begin{align*}
\varphi_{n,q}(x + na) &= \frac{1}{\sqrt{Na}}\sum_K c_{n,q-K}e^{i(q-K)x}e^{i(q-K)na}\\
&=
\frac{1}{\sqrt{Na}}\sum_K c_{n,q-K}e^{i(q-K)x}e^{iqna}\\
&=
e^{iqna}\varphi_{n,q}(x)
\end{align*}
を満たします。また、
\varphi_{n,q}(x) = \frac{1}{\sqrt{Na}}e^{iqx}\sum_K c_{n,q-K}e^{-iKx}
と書くと、右辺\frac{1}{\sqrt{Na}}e^{iqx}を除いた部分は
\sum_K c_{n,q-K}e^{-iK(x + na)} = \sum_K c_{n,q-K}e^{-iKx}e^{-iKna}
=
\sum_K c_{n,q-K}e^{-iK(x)}
を満たし、結晶の周期性を持つ関数u_{n,q}(x)と書けます。
以上で、ブロッホの定理として示した前半部分
を示すことができました。「ブロッホ波数」についての説明や波数空間での周期性の話に移る前に、先に3次元版でも同様に考えておきます。
3次元の場合のブロッホの定理の証明
上記で1次元の場合についてブロッホの定理を示しましたが、3次元の場合も以下の点を変えれば同じ流れで考えることができます。
ポテンシャルU(\boldsymbol{r})のFourier展開は前章で行ったように逆格子ベクトル\boldsymbol{K}:
\boldsymbol{K}
=
m_1\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)}
+
m_2\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)}
+
m_3\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}
を用いた
U(\boldsymbol{r}) = \sum_{\boldsymbol{K}}U_{\boldsymbol{K}}e^{i\boldsymbol{K}\cdot\boldsymbol{r}}
となります。
また、波動関数\varphi(\boldsymbol{r})の境界条件として、先ほど考えた条件の3次元版、すなわち基本併進ベクトルを\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3としたとき、十分大きな数N_1, N_2, N_3 (N_1\times N_2\times N_3 \times v_c (単位胞の体積)が大体結晶のサイズになるくらい)を考え、
\varphi(\boldsymbol{r} + N_i\boldsymbol{a}_i) = \varphi(\boldsymbol{r})
という条件を考えます。すると逆格子ベクトルと1/N_i異なる波数ベクトル
\begin{align*}
\boldsymbol{q}
&=
m_1\frac{2\pi N_2\boldsymbol{a}_2\times N_3\boldsymbol{a}_3}{ N_1\boldsymbol{a}_1\cdot( N_2\boldsymbol{a}_2\times N_3\boldsymbol{a}_3)}
+
m_2\frac{2\pi N_3\boldsymbol{a}_3\times N_1\boldsymbol{a}_1}{ N_2\boldsymbol{a}_2\cdot( N_3\boldsymbol{a}_3\times N_1\boldsymbol{a}_1)}
+
m_3\frac{2\pi N_1\boldsymbol{a}_1\times N_2\boldsymbol{a}_2}{ N_3\boldsymbol{a}_3\cdot( N_1\boldsymbol{a}_1\times N_2\boldsymbol{a}_2)}\\
&=
\frac{m_1}{N_1}\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)}
+
\frac{m_2}{N_2}\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)}
+
\frac{m_3}{N_3}\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}
\end{align*}
の平面波e^{i\boldsymbol{q}\cdot \boldsymbol{r}}を用いて以下のように展開できます:
\varphi(\boldsymbol{r}) = \frac{1}{\sqrt{V}}\sum_{\boldsymbol{q}}c_{\boldsymbol{q}}e^{i\boldsymbol{q}\cdot\boldsymbol{r}}
ここで\frac{1}{\sqrt{V}}は規格化のための係数で、結晶の単位胞の体積v_c = \boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)のN=N_1N_2N_3倍の定数です。これらをシュレーディンガー方程式に代入して整理すると、運動エネルギー項に対しては
\nabla^2\sum_{\boldsymbol{q}}c_{\boldsymbol{q}}e^{i\boldsymbol{q}\cdot\boldsymbol{r}}
=
\sum_{\boldsymbol{q}}q^2c_{\boldsymbol{q}}e^{i\boldsymbol{q}\cdot\boldsymbol{r}}
となります。またポテンシャル項について、
\begin{align*}
U(\boldsymbol{r})\varphi(\boldsymbol{r})
&=
\frac{1}{\sqrt{V}}
\sum_{\boldsymbol{K}}\sum_{\boldsymbol{q}}U_{\boldsymbol{K}}
c_{\boldsymbol{q}}
e^{i(\boldsymbol{K}+\boldsymbol{q})\cdot\boldsymbol{r}}\\
&=
\frac{1}{\sqrt{V}}
\sum_{\boldsymbol{K}}\sum_{\boldsymbol{q}'}U_{\boldsymbol{K}}
c_{\boldsymbol{q}'-\boldsymbol{K}}
e^{i\boldsymbol{q}'\cdot\boldsymbol{r}}\\
\end{align*}
ですが、\boldsymbol{q}+\boldsymbol{K}\rightarrow\boldsymbol{q}'の置き換えに対しても\sum_{\boldsymbol{q}'}の和の範囲は変わらないので、改めて\boldsymbol{q}'\rightarrow\boldsymbol{q}と置きなおして、
U(\boldsymbol{r})\varphi(\boldsymbol{r})
=
\frac{1}{\sqrt{V}}
\sum_{\boldsymbol{K}}\sum_{\boldsymbol{q}}U_{\boldsymbol{K}}
c_{\boldsymbol{q}-\boldsymbol{K}}
e^{i\boldsymbol{q}\cdot\boldsymbol{r}}\\
と書けます。これらをまとめて、波数表示のシュレーディンガー方程式を
\frac{1}{\sqrt{V}}
\sum_{\boldsymbol{q}}e^{i\boldsymbol{q}\cdot\boldsymbol{r}}
\left[
(\frac{\hbar^2}{2m}q^2 - \varepsilon)c_{\boldsymbol{q}} +
\sum_{\boldsymbol{K}}U_{\boldsymbol{K}}
c_{\boldsymbol{q}-\boldsymbol{K}}
\right]
=0
と書き換えることができ、Fourier係数c_{\boldsymbol{q}}の満たす方程式
(\frac{\hbar^2}{2m}q^2 - \varepsilon)c_{\boldsymbol{q}} +
\sum_{\boldsymbol{K}}U_{\boldsymbol{K}}
c_{\boldsymbol{q}-\boldsymbol{K}} = 0
を得ることができます。ここから、逆格子ベクトルに何らかの順番を考えて行列表示で考えれば1次元の場合と同様に、値が小さい順に振られたラベルnと、方程式を指定する波数\boldsymbol{q}に対応する固有値\varepsilon_{n,\boldsymbol{q}}が得られ、それに対応して波数\boldsymbol{q}と、その逆格子ベクトルだけ異なるFourier級数からなるブロッホ関数
\varphi_{n,\boldsymbol{q}}(\boldsymbol{r}) = \frac{1}{\sqrt{V}}\sum_{\boldsymbol{K}}c_{n,\boldsymbol{q} - \boldsymbol{K}}
e^{i(\boldsymbol{q} - \boldsymbol{K} )\cdot \boldsymbol{r}}
を固有関数として導くことができます。
この関数に対して格子ベクトルの並進を考えることで、1次元の場合と同様に
\varphi_{n,\boldsymbol{q}}(\boldsymbol{r} + \boldsymbol{n}) = e^{i\boldsymbol{k}\cdot\boldsymbol{n}}
\varphi_{n,\boldsymbol{k}}(\boldsymbol{r})
を満たすことが確認できます。さらに、
u_{n,\boldsymbol{q}}(\boldsymbol{r}) \equiv
\sum_{\boldsymbol{K}}c_{n,\boldsymbol{q} - \boldsymbol{K}}
e^{-i \boldsymbol{K} \cdot \boldsymbol{r}}
が結晶の周期性を持つ
u_{n,\boldsymbol{q}}(\boldsymbol{r} + \boldsymbol{n}) = u_{n,\boldsymbol{q}}(\boldsymbol{r})
ことが示せます。
ブリルアンゾーン
さて、ここまでラベルqまたは\boldsymbol{q}の選び方に関して特に注意を払っておりませんでしたが、以下のように考えることで、固有エネルギー・固有関数が波数\boldsymbol{q}に関して、逆格子ベクトルの周期性を持っていると考えることができます。
すなわち、先ほどブロッホの定理として示した内容の後半部分、
が成立していることを本節で確認し、その流れで「ブリルアンゾーン」という概念を導入します。
固有値・固有関数の波数空間での周期性(1次元版)(ブロッホの定理後半の証明)
初めに、例によってあまりややこしくない1次元の場合から考えていきます。先ほど考えた1次元の場合のブロッホ関数の導出を思い出してみると、あるラベルqを選ぶとその逆格子分だけ異なる波数のみから係数c_{q+K}に関する方程式ブロック
\begin{bmatrix}
\ddots & & & & \\
& \ddots & \\
& & \ddots & & &\\
& & & \ddots \\
\cdots & \cdots & U_{-K_2} & U_{-K_1} & \frac{\hbar^2}{2m}q^2 + U_0 & U_{K_1} & U_{K_2}&\cdots \\
\\
& & &&& \ddots & \\
&& & & &&\ddots & \\
&&& & & &&\ddots & \\
\end{bmatrix}
\begin{bmatrix}
\vdots \\
c_{q - K_m} \\
\vdots \\
c_q \\
\vdots \\
c_{q + K_m} \\
\vdots
\end{bmatrix}
= \varepsilon
\begin{bmatrix}
\vdots \\
c_{q - K_m} \\
\vdots \\
c_q \\
\vdots \\
c_{q + K_m} \\
\vdots
\end{bmatrix}
が形成されるのでした。
一方、例えば先ほど選んだqに対して、ある逆格子分だけ異なるq' = q - K_lに対する方程式
(\frac{\hbar^2}{2m}(q-K_l)^2 - \varepsilon)c_{q-K_l} +
\sum_{K'}U_{K'}
c_{q-K_l-K'} = 0
を考えてみたとします。
そうした場合も、先ほどと同じようにq'から全ての逆格子分だけ異なる係数からなる連立方程式ブロック
\begin{bmatrix}
\ddots & & & & \\
& \ddots & \\
& & \ddots & & &\\
& & & \ddots \\
\cdots & \cdots & U_{-K_{l+2}} & U_{-K_{l+1}} & \frac{\hbar^2}{2m}(q-K_l)^2 + U_{K_{l}} & U_{K_{l+1}} & U_{K_{l+2}}&\cdots \\
\\
& & &&& \ddots & \\
&& & & &&\ddots & \\
&&& & & &&\ddots & \\
\end{bmatrix}
\begin{bmatrix}
\vdots \\
c_{q - K_l- K_m} \\
\vdots \\
c_{q-K_l} \\
\vdots \\
c_{q - K_l + K_m} \\
\vdots
\end{bmatrix}
= \varepsilon
\begin{bmatrix}
\vdots \\
c_{q - K_l- K_m} \\
\vdots \\
c_{q-K_l} \\
\vdots \\
c_{q - K_l + K_m} \\
\vdots
\end{bmatrix}
を得ることができますが、その中には必ず先に選んだq = q' + K_lも含まれており、結局全ての方程式を参照すると全く同じ式の集まりであることがわかります。
ラベルnについては値が小さい順に振ると決めてありましたので、その方程式から作られる行列の固有値\varepsilon_{n,q'}も、固有関数\varphi_{n,q'}(x)も先に考えた固有値\varepsilon_{n,q}も、固有関数\varphi_{n,q}(x)と全く同じものになります。
これはある波数qを選んで得た(無限個のnでラベルされた)固有値\varepsilon_{n,q}、固有関数\varphi_{n,q}と、先ほどの波数から逆格子だけ異なる波数q-Kを選んで得た固有値\varepsilon_{n,q-K}、固有関数\varphi_{n,q-K}が一致していることを意味しています。ラベルqは方程式を指定するラベルであり、逆格子分ずれたラベルからは同じ方程式が指定されるわけです。
そこで、ラベルqに関しては「逆格子の周期の最小単位の領域に含まれるqのみを考えればよい」ということになります。
図式的に表すと、下図のようにある波数、特にk = 0を選ぶと、それに対応して逆格子\pm K_1, \pm K_2\cdotsだけ異なる波数k = \pm K_1, \pm K_2\cdotsの方程式の組が得られるので、k = 0を中心に逆格子の周期性の最小単位のkを選べば全てのkに対する方程式が得られる、と考えられます。
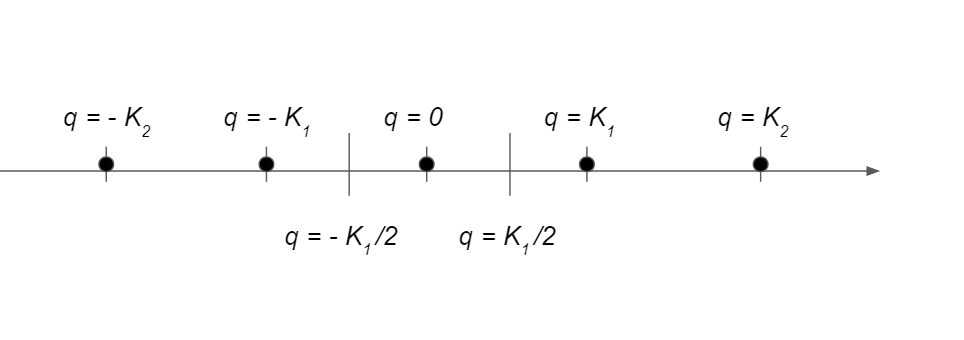
あるいは少し考えを拡張して、波数ベクトルqをラベルとする固有値、固有関数は、波数空間内で逆格子の周期性
\varepsilon_{n,q + K} = \varepsilon_{n,q},\\
\varphi_{n,q + K}(x) = \varphi_{n,q}(x)
を持つ周期関数であるとも考えることができます。
周期関数であれば、関数を考える際やグラフで表示する際、1周期分のみを考えれば良いわけです。
いずれにしても、波数空間の周期の最小単位内の波数を代表して選べば、全ての波数に対する方程式が得られることがわかります。
そのような波数空間における単位胞内の波数を「ブロッホ波数」と呼び、記号kで表します。
そして周期の最小単位の領域のことをブリルアンゾーンと呼び、特に原点を中心として、隣接する逆格子点との垂直二等分面(2次元だと線、1次元だと点)で区切られた領域を第一ブリルアンゾーンと呼びます。
固有値・固有関数の波数空間での周期性(3次元版)
3次元で考えた場合も、先ほどと同様に、ある波数ベクトル\boldsymbol{q}に対して得られる方程式ブロックと、逆格子ベクトルだけ異なる\boldsymbol{q} - \boldsymbol{K}に対して得られる方程式ブロックが等しく、その結果固有エネルギー\varepsilon_{n,\boldsymbol{q}}、ブロッホ関数\varphi_{n,\boldsymbol{q}}(\boldsymbol{r})が逆格子ベクトルの周期を持つことがわかります。
さて、1次元の場合はただ隣接する逆格子点までの中点にはさまれた領域を考えればよかったですが、3次元の場合はどのような領域を考えればよいでしょうか。
素朴には、最小単位であれば良いので逆格子ベクトル
\begin{align*}
\boldsymbol{K}
&=
m_1\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)}
+
m_2\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)}
+
m_3\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}\\
&=m_1\boldsymbol{b}_1 + m_2\boldsymbol{b}_2 + m_3\boldsymbol{b}_3
\end{align*}
に対して、領域
\boldsymbol{k} = s\boldsymbol{b}_1 + t\boldsymbol{b}_2 + u\boldsymbol{b}_3,\\
0\leq s < 1, 0\leq t < 1, 0\leq u < 1
の単位胞内の\boldsymbol{k}を考えればあとは逆格子ベクトルを足し引きすれば全ての波数\boldsymbol{q}をカバーできるわけですが、それよりももっと性質の良い単位胞の取り方として、1次元版でちらっと述べたように
「原点から隣接する全ての逆格子ベクトルに対する垂直2等分面を考え、その面に囲まれる領域」
という単位胞を考えます。このような単位胞を「Wigner-Seitz cell(ウィグナー・サイツ・セル)」と呼び、特に波数空間におけるWigner-Seitz cellをブリルアンゾーン、その原点から最も近い領域を第一ブリルアンゾーンと呼びます。
そして、このような(第一)ブリルアンゾーン内で定義された波数ベクトルを「ブロッホ波数」と呼び、記号\boldsymbol{k}を用いて表します。
ここはあまり深く突っ込まないのですが、なぜこんなややこしいことをするかというと、Wigner-Seitz cellはあるブラベー格子(これは実空間の格子であっても逆格子空間の逆格子ベクトルの集まりであっても)を考えた際に、そのブラベー格子が持つ対称性と等しい対称性を持つ、という性質があるからのようです。
この辺はいずれ、ちゃんと勉強して何かしら追記しますが、この段階ではひとまずこんなところで。
補足として、ここまでの流れでわかるように(ブロッホ)波数は、「ある「連立方程式ブロック」を代表する波数」という意味ですので、ラベルが直接関数を指定していた自由電子の波動関数\varphi_k(x) = Ae^{ikx}や中心力場内の電子の固有関数\varphi_{nml} = R_{nl}Y_l^mとは若干違う意味合いで使われおり、「方程式群を指定するラベル」kと、「そこから得られる関数を指定するラベルn」というセットとなっております。
その上に自由電子と全く同じラベルが使われているので中々ややこしいなと感じますが、「結晶内の波数っぽい物理量に対応している」的な意味で自由電子の波数と同じ記号が使われ、「結晶運動量」等と呼ばれたりしているようです。(先述の通り本稿では今のところはここも深く突っ込まないことにします)
さて、話を戻して、以上で格子の周期を持つハミルトニアンの下での固有値、固有ベクトルの性質であるブロッホの定理
が成り立つことを確認できました。
エネルギーバンド
最後に、エネルギー固有値\varepsilon_{n,\boldsymbol{k}}の持つ性質から、ブロッホ波数に対してプロットしたブロッホ電子の固有エネルギーの性質を確認して終わりにします。
表題の通り、エネルギー固有値\varepsilon_{n,\boldsymbol{k}}は、ブロッホ波数に対して「帯(バンド)」のようなグラフでプロットされます。
これはどのようにして\varepsilon_{n,\boldsymbol{k}}を求めたかを考えればよく、ブロッホ波数\boldsymbol{k}(第一ブリルアンゾーン内の波数に限ることを反映して、ここでは\boldsymbol{k}を使います)をパラメータとして持つ行列H_{\boldsymbol{k}}の固有値方程式
|H_{\boldsymbol{k}} - \varepsilon I| = 0
の(無限個の)根として\varepsilon_{n,\boldsymbol{k}}が得られたのでした。
この時、パラメータに依存した行列の固有値はそのパラメータに対して連続かつ微分可能である、らしいです。
突然自信を失って申し訳ありません。 このあたりの証明がよくわかっていないので、ここは曖昧なままにしてしまいます。いずれ線形代数か量子力学の最初の方か色々読み返して、ちゃんとやります。
またこちらも全く曖昧なのですが、行列H_{\boldsymbol{k}}の対角要素\frac{\hbar^2}{2m}(\boldsymbol{q} - \boldsymbol{K})^2の逆格子ベクトル\boldsymbol{K}が離散的であることから、対角化して得られる固有値\varepsilon_nはnに対して離散的になる、らしいです。
全く正確ではないと思うのですが、今のところは次のように考えてみます。すなわち、行列式
|H_{\boldsymbol{k}} - \varepsilon I|=0
を\varepsilonの多項式として考えてみると、
\cdots + A(\boldsymbol{k})\varepsilon^n + A'(\boldsymbol{k})\varepsilon^{n-1} + \cdots = 0
みたいな方程式になるわけですが、この根は上記方程式左辺を\varepsilonの関数としてプロットした場合に横軸との交点になるわけで、まあ確かに、\boldsymbol{k}の変化に対して滑らかに交点は変化しそうですし、交点は離散的になりそうな気がします。
あるいは、もう少し物理的に考えると、周期ポテンシャルを無視(U(\boldsymbol{r})\rightarrow 0)した場合(これは「空格子モデル」等と呼ばれます。)、行列H_{\boldsymbol{k}}は対角化されたものとなります。すなわち行列の固有ベクトルは、
\begin{bmatrix}
\vdots \\
c_{q - K_m} \\
\vdots \\
c_q \\
\vdots \\
c_{q + K_m} \\
\vdots
\end{bmatrix}
のうち、1つの係数c_{q-K_m}のみが1となり、残りは0であるような場合に対応します。
というか、これは自由電子の固有関数
\varphi_{n,\boldsymbol{k}} = \frac{1}{\sqrt{V}}c_{n, \boldsymbol{k}- \boldsymbol{K}}e^{i(\boldsymbol{k} - \boldsymbol{K})\cdot\boldsymbol{r}}
で、ポテンシャルがない場合を考えているので当然そうなります。
さて、自由電子のハミルトニアンにはなりましたが、一応先ほどと同じ「ブロック」は残っているのでブロッホ波数\boldsymbol{k}で指定されるブロックを対角化した固有値\varepsilon_{n,\boldsymbol{k}}について考えてみると、これは逆格子ベクトルと一対一で対応し
\varepsilon_{n,\boldsymbol{k}} = \cdots , \frac{\hbar^2}{2m}(\boldsymbol{k} - \boldsymbol{K_m})^2 , \frac{\hbar^2}{2m}(\boldsymbol{k} - \boldsymbol{K_{m-1}})^2 , \cdots, \frac{\hbar^2}{2m}\boldsymbol{k}^2 ,\cdots, \frac{\hbar^2}{2m}(\boldsymbol{k} + \boldsymbol{K_m})^2 , \cdots
となります(一応注意として、ラベルnは|\boldsymbol{k} - \boldsymbol{K}_m|が小さい順に振られるので、上記の順番とラベルnの順番は異なります)。
この時固有エネルギーは明らかにブロッホ波数に対して連続かつ微分可能な滑らかな関数です。
なお、ブロッホ波数も周期的境界条件に対応して離散的な変数で定義されていますが、関数形としては「\boldsymbol{k}について滑らか」であるといえますし、また「十分大きな系を考える」周期的境界条件という前提のもと、N\rightarrow\inftyと考えるので実質的には\boldsymbol{k}は連続変数であると考えることになります。
また固有エネルギーのnに対する変化は、この場合は逆格子ベクトルの変化と一致しますが、逆格子ベクトル
\boldsymbol{K}
=
m_1\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)}
+
m_2\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)}
+
m_3\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}
と、ブロッホ波数
\begin{align*}
\boldsymbol{k}
&=
\frac{m_1}{N_1}\frac{2\pi\boldsymbol{a}_2\times\boldsymbol{a}_3}{\boldsymbol{a}_1\cdot(\boldsymbol{a}_2\times\boldsymbol{a}_3)}
+
\frac{m_2}{N_2}\frac{2\pi\boldsymbol{a}_3\times\boldsymbol{a}_1}{\boldsymbol{a}_2\cdot(\boldsymbol{a}_3\times\boldsymbol{a}_1)}
+
\frac{m_3}{N_3}\frac{2\pi\boldsymbol{a}_1\times\boldsymbol{a}_2}{\boldsymbol{a}_3\cdot(\boldsymbol{a}_1\times\boldsymbol{a}_2)}
\end{align*}
はざっくり逆格子の方がN_i倍程度大きいので、ブロッホ波数の変化に対するエネルギー固有値の変化に比べて、ラベルnの変化=逆格子ベクトル\boldsymbol{K}の変化に対するエネルギー固有値の変化は離散的であると考えられます。
以上のように考えてみても、エネルギー固有値\varepsilon_{n,\boldsymbol{k}}の性質をなんとなくイメージできるかと思います。本当はもっとシンプルな証明があるのだろうと思いますが、その辺はいずれ追記したいところです。
さて話を戻して、以上から、ブロッホ波数\boldsymbol{k}に対するエネルギー固有値の変化を描いた場合、
- 各\boldsymbol{k}点に対して、複数のエネルギー固有値が飛び飛びにプロットされ
- かつ波数\boldsymbol{k}に関しては連続かつ各点で微分可能な滑らかなグラフ
で表されるはずです。1次元の場合は曲線、2次元の場合は曲面でプロットされ、グラフは\boldsymbol{k}空間に広がった帯(バンド)のような形状になりそうだと分かりました。そのような性質から、固体内のエネルギー分散を「エネルギーバンド」と呼びます。
この辺りは、次章でもう少し補足しようと思います。
おわりに
本章では、結晶内の電子の性質を考える出発点として、「結晶の周期性を持つポテンシャルの下で電子の波動関数が一般的に持つ性質」としてブロッホの定理を示し、またブロッホの定理に従う波動関数やそのエネルギー固有値の性質を考えることでブリルアンゾーン・エネルギーバンドの概念を導入しました。
これにより固体内の多電子状態に対して「原子核+内殻電子からの相互作用を1粒子ポテンシャルとして近似する」「価電子間の相互作用を無視する」として、相互作用しない状態に近似し、1電子シュレディンガー方程式へ帰着させた際に、そのシュレディンガー方程式において電子がとるべき状態について理解することができました。
まとめとして再掲すると、
格子ベクトル
\begin{align*}
\boldsymbol{n} &= n_1\boldsymbol{a}_1 + n_2\boldsymbol{a}_2 + n_3\boldsymbol{a}_3\\
\end{align*}
に対して
U(\boldsymbol{r} + \boldsymbol{n}) = U(\boldsymbol{r})
を満たすポテンシャルの下でのシュレーディンガー方程式
\hat{H}\varphi(\boldsymbol{r}) = \varepsilon\varphi(\boldsymbol{r}),\\
\hat{H} =
-\frac{\hbar^2}{2m}\nabla^2
+
U(\boldsymbol{r})
に対して、波動関数は以下のブロッホの定理を満たします。
また、ブリルアンゾーン・エネルギーバンドとして
というような内容でした。
複数の内容を駆け足で1記事に詰め込んだ感があり、多くの教科書で語られている内容を端折りまくったものとなりましたが、最低限の内容にはなったかなと思います。
何か不明点や間違い・勘違い・その他感想などありましたら是非コメントなどで教えていただけますとありがたいです。

Discussion