pokapoka-jigoku

発端

pokapoka-jigoku

Zipf分布のエントロピーを求めようとした。

本質ではないので書くのは後回しにするが、エントロピーの漸化式を求めていた。

Spread sheet

pokapoka-jigoku

Wikipedia によれば、Zipf分布のエントロピーは：

S_n = \frac{1}{H_n} \sum_{k=1}^{n} \frac{\ln k}{k} + \ln H_n

である。総和の部分を：

\sum_{k=1}^{n} \frac{\ln k}{k} \approx \int_1^x {\frac{\ln t}{t}} dt = \frac{(\ln x)^2}{2}

さらに、調和数を：

H_n \approx \ln \left(n + \frac{1}{2}\right) + \gamma \approx \ln n + \gamma

ただし、 $\gamma = 0.57721 56649...$ はオイラーマスケローニ定数(Wikipedia)。

これらを用いて：

\begin{split} S_n &\approx \frac{(\ln n)^2}{2 (\ln n + \gamma)} + \ln (\ln n + \gamma) \\ &= \frac{(\ln n + \gamma)}{2} \left( 1 - \frac{\gamma}{\ln n + \gamma} \right)^2 + \ln (\ln n + \gamma) \\ \end{split}

pokapoka-jigoku

考え方

総単語数Nの言語を使って、M語からなる文章を作ることを考える。文法構造ないし非文かどうかを全く考慮せず、単純な組合せ論的な場合の数は、情報エントロピーを $S$ として、ほぼ $\exp(SM)$ になる。

仮に等確率の場合は、 $S=\ln N$ なので、場合の数は $\exp(M \ln N) = N^M$ になる。

一般のエントロピーでは、場合の数は $(\exp S)^M$ で表せることを考えると、 $\exp S$ が情報論的な単語数 $N^*$ を表していると解釈できる。

参考：EMANの物理学 - 情報エントロピー

pokapoka-jigoku

総単語数Nのとき、これらの単語の使用率が厳密にZipf分布に従うとする（Ziphil-Zipfの仮定）と、上記の議論から、情報論的単語数 $N^*$ は

\begin{split} N^* &= \exp S_n = \exp \left( \frac{(\ln n + \gamma)}{2} \left( 1 - \frac{\gamma}{\ln n + \gamma} \right)^2 + \ln (\ln n + \gamma) \right) \\ &= (\ln n + \gamma) \exp \left( \frac{(\ln n + \gamma)}{2} \left( 1 - \frac{\gamma}{\ln n + \gamma} \right)^2 \right) \\ &= (\ln n + \gamma) \exp \left( \frac{(\ln n + \gamma)}{2} - \gamma \right) \\ &= (\ln n + \gamma) \exp \left( \frac{\ln n - \gamma}{2}\right) \\ &= \ln (ne^{\gamma}) \sqrt{\frac{n}{e^\gamma}} \\ &= e^{-\gamma} \ln (ne^{\gamma}) \sqrt{ne^{\gamma}} \end{split}

$e^\gamma = 1.78107241799019798...$ なので、

\begin{split} N^* &= \ln (1.781N) \sqrt{\frac{N}{1.781}}\\ &= \frac{1}{1.781} \ln (1.781N) \sqrt{1.781N} \end{split}

となる。あるいは、補正付き単語数 $\eta = e^\gamma n$ を定義して、

\eta^* = \sqrt{\eta} \ln \eta

としてもよい。

pokapoka-jigoku

グラフ

pokapoka-jigoku

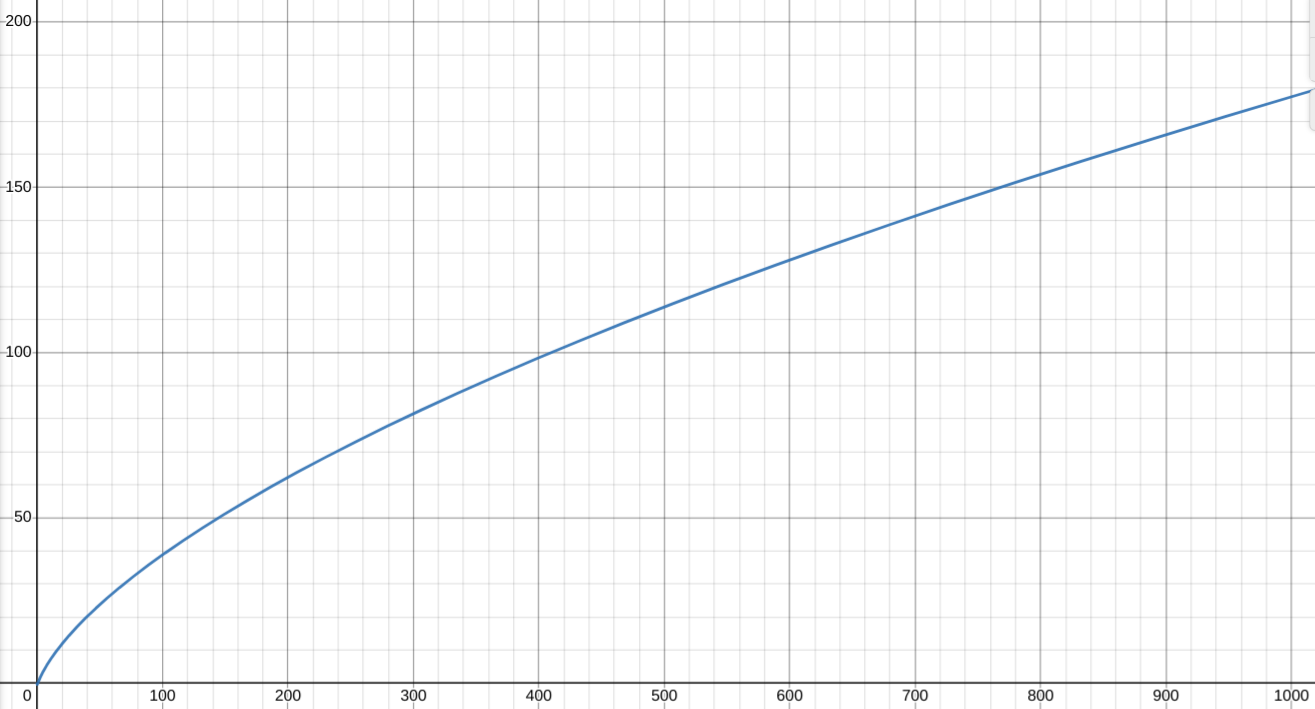
両対数グラフ（常用対数）

pokapoka-jigoku

Discussion

1TP = 120 words は、 $\eta = 1.781 \cdot 120 = 213.6$ なので

N^* = \frac{1}{1.781} \sqrt{213.6} \ln 213.6 = 44.018

pokapoka-jigoku

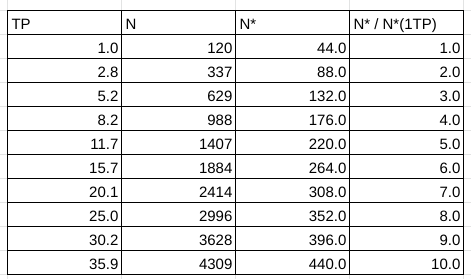
TPごとに情報論的単語数を考えると：

pokapoka-jigoku

なんらかの単位があるほうが導入しやすいと思うので、Zipfied words point ということで、ZPを提案する。

pokapoka-jigoku

新しい単語数のLvとして、情報論的単語数レベル　LvZを提案する。

これは1TP（120words）での情報論的単語数 44.0 を基準に、その倍数の情報論的単語数を得られるのに必要な単語数の閾値を定める。

pokapoka-jigoku

楽観的評価

Zipfの法則がどこまで通用するものなのかはあまり知らないけど、文章作成における諸々の制約（文法、文体、共起表現など）を通じた結果、Zipfの法則が成り立つようになってしまうとしたら、今回求めた情報論的単語数は案外バカにならない指標かもしれない

pokapoka-jigoku

つまり、たとえば1TP = 120 words = 44ZP の言語では、100単語レベルの文章を書こうとすると、常用対数で $100 \log 44 = 164.34$ のテキストぐらいしか生成できないということかもしれない。

pokapoka-jigoku

数が膨大でイメージしにくいかもしれないが…、もし素朴に総単語数 120語の無機質な組合せ論を考えると、100語文のレパートリーは $100 \log 120 = 207.92$ 程度に及ぶ。

この比を考えると、 $100 \log 44 - 100 \log 120 = -43.57$ で生成できる文章の数はとてつもなく小さくなっていることが分かる。

pokapoka-jigoku

もう少し厳密に

上記の議論では、 $O(\ln M)$ の項をバッサリ削っていたので、スターリングの近似を：

\ln x! = x \ln x - x + \frac{1}{2} \ln 2\pi x + O(x^{-1})

として、近似精度をあげて計算してみる。結論としては、

\begin{split} \ln W^* = &S_N(p) - \frac{N-1}{2M} \ln 2\pi M \\ &+ \frac{N}{2M} \left( \ln N - 1 + \frac{\ln 2 \pi N}{2N} + \ln (\ln N + \gamma) \right) + O(M^{-1}) \end{split}

となる。 $M \gg 1$ のとき、上記の議論の通りになり、情報論的単語数は $S_N(p)$ に一致する。

pokapoka-jigoku

過程を書くと、スターリングの近似のlog項由来で：

\begin{split} M \ln W^* &= M S_N(p) + \frac{1}{2} \ln 2\pi M - \sum_{i=1}^N \frac{1}{2} \ln 2\pi k_i \\ &= M S_N(p) -\frac{N-1}{2} \ln 2\pi M - \frac{1}{2} \sum_{i=1}^N \ln \frac{(1/i)}{H_N} \\ &= M S_N(p) -\frac{N-1}{2} \ln 2\pi M + \frac{1}{2} (\ln N! + N\ln H_N) \\ &= M S_N(p) -\frac{N-1}{2} \ln 2\pi M \\ &~~~~+ \frac{N}{2} (\ln N - 1 +\frac{\ln 2\pi N}{2N} + \ln (\ln N + \gamma)) \\ \end{split}

Hidden comment

pokapoka-jigoku

少し整理。 $\frac{N-1}{2M} \approx \frac{N}{2M}$ として：

\begin{split} \ln W^* &\approx S_N(p) + \frac{N}{2M} \left( \ln N - 1 + \frac{\ln 2 \pi N}{2N} + \ln (\ln N + \gamma) - \ln 2\pi M \right) + O(M^{-1}) \\ &= S_N(p) + \frac{N}{2M} \left( \ln \left( \frac{N}{2\pi M} (\ln N + \gamma) \right) + \frac{\ln 2 \pi N}{2N} -1 \right) + O(M^{-1}) \end{split}

pokapoka-jigoku

数値実験。

大体 $M=300N$ ぐらいで、ほとんど第二項は無視できそう：

pokapoka-jigoku

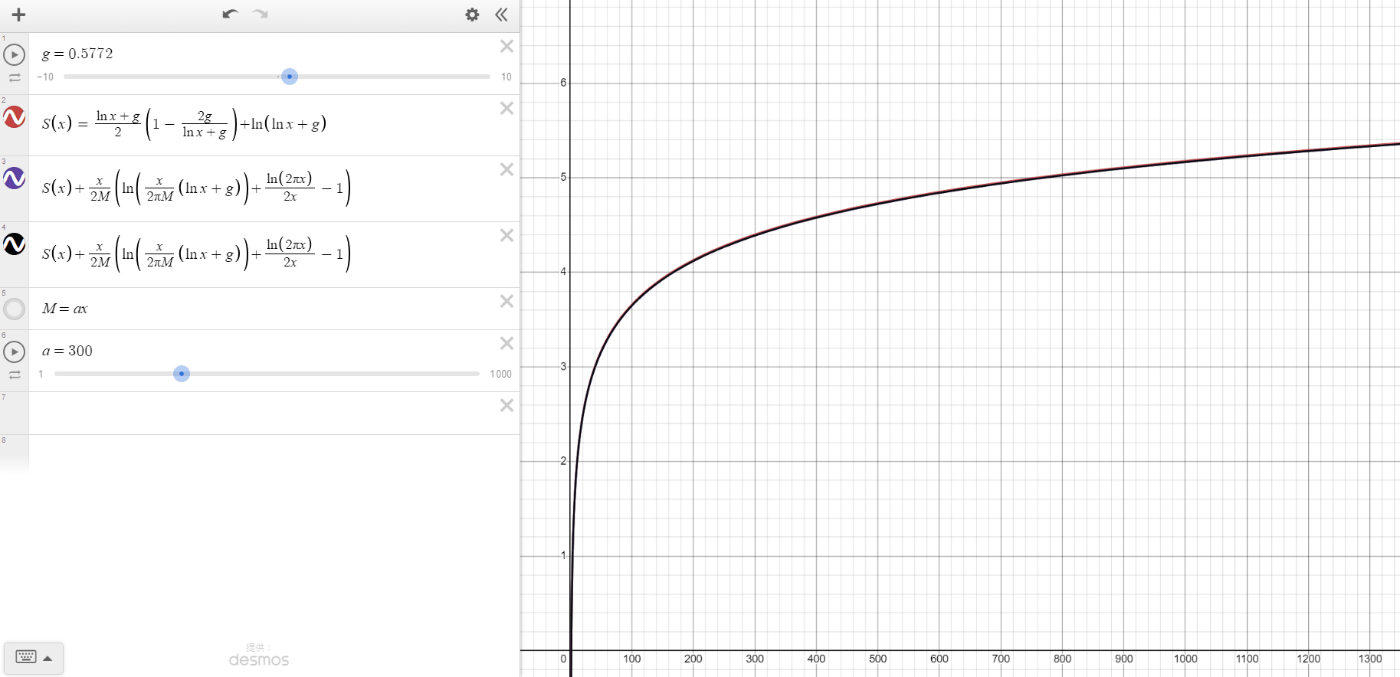
50Nだと結構目立つ

pokapoka-jigoku

第二項目の近似。実験的に：

\frac{1}{2a} \ln \left( \frac{\ln N + \gamma}{2\pi e a} \right)

ここで、 $a = M/N$ 。

＊条件

$N \ge 300$ なら、 $a \ge 0.5$ のほぼ全領域でよい近似。
$N \ge 30$ なら、 $a \ge 5$ でよい近似になる。

pokapoka-jigoku

よって、全体として：

\ln W^* = S_N(p) + \frac{1}{2a} \ln \left( \frac{\ln N + \gamma}{2\pi e a} \right)

\begin{split} W^* &= e^{-\gamma} \ln (Ne^{\gamma}) \sqrt{Ne^{\gamma}} \cdot \left( \frac{\ln N + \gamma}{2\pi e a} \right)^{\frac{1}{2a}} \\ &= e^{-\gamma} \ln (Ne^{\gamma}) \sqrt{Ne^{\gamma}} \cdot \left( \frac{N\ln N + \gamma N}{2\pi e M} \right)^{\frac{N}{2M}} \\ &= e^{-\gamma} \ln (Ne^{\gamma}) \sqrt{Ne^{\gamma}} \cdot \left( \frac{N}{2M} \right)^{\frac{N}{2M}} \left( \frac{\ln N + \gamma}{\pi e} \right)^{\frac{N}{2M}} \end{split}

pokapoka-jigoku

$N \le 20000$ 程度であれば、 $M = a N$ のもとで、

\left( \frac{\ln N + \gamma}{\pi e} \right)^{\frac{N}{2M}} \approx 1

よって、

W^* = e^{-\gamma} \ln (Ne^{\gamma}) \sqrt{Ne^{\gamma}} \cdot (2a)^{-\frac{1}{2a}}