このアカウントは事あるごとに多項係数を評価しようとしている：

過去の記事では $k_i=0$ のケースをカバーするために、Nemesの近似変形式を使って頑張っていた：

ただ我に返ると：

\ln x! \approx x \ln x - x + \frac{1}{2} \ln {2\pi x} + \frac{1}{12x}

であっても、 $x \ge 1$ で十分にいい近似になるので、スターリング近似で戦えるのでは？と思い直してこの記事を書いている。つまりこのスクラップでやりたいことは

$k_i \ge 1$ 条件下での、スターリング近似を用いた多項係数の評価
$k_i = 0$ を含む場合の処理
（発展）連続分布への対応

である。

pokapoka-jigoku

1. について

散々やり尽くした計算なので結果だけ書きたい。 $N$ 回のサンプリング、 $r$ 種の項目で、すべての項目の出る目が $k_i \ge 1$ であるとする。

\ln W = \ln \frac{N!}{k_1! ..... k_r!} \approx - \sum_i^r \frac{k_i}{N} \ln \frac{k_i}{N} - \frac{r-1}{2} \ln 2\pi + \frac{1}{2} K_1 + \frac{1}{12} K_2

ここで、

K_1 = \ln N - \sum_i^r \ln k_i

K_2 = \frac{1}{N} - \sum_i^r \frac{1}{k_i}

さて、

q_i = \frac{k_i}{N}

とおけば、

\ln W = - N\sum_i^r q_i \ln q_i - \frac{r-1}{2} \ln 2\pi N + \frac{1}{2} Q_1 + \frac{1}{12N} Q_2

Q_1 = - \sum_i^r \ln q_i

Q_2 = 1-\sum_i^r \frac{1}{q_i}

pokapoka-jigoku

第１項（エントロピー）は正
第２項は負
Q1項は正
Q2項は負

Hidden comment

pokapoka-jigoku

確率分布の偏差に対する法線ベクトル

\iota = (1, 1, ..., 1)^T

に対するエントロピーの方向微分は、

\nabla_{\iota} S = - \sum_i \ln q_i - r

さらにこの方向微分は、

\nabla^2_{\iota} S = - \sum_i \frac{1}{q_i}

であるから、

Q_1 = r + \nabla_{\iota} S\\ Q_2 = 1 + \nabla^2_{\iota} S

である。

pokapoka-jigoku

補足）

確率分布の偏差、 $\Delta q = (\Delta q_i)_i$ は総和が零なので、 $\Delta q \cdot \iota = 0$ である。

pokapoka-jigoku

余談）
確率の制約から、確率分布 $q = (q_i)_i$ と $\iota$ の内積は、 $q \cdot \iota = 1$ である。

このように $\iota$ と確率分布には結構関連がある。

pokapoka-jigoku

小括

よって、

\ln W = N \cdot S(q) - \frac{r-1}{2} \ln 2\pi N + \frac{1}{2} \left( r + \nabla_{\iota} S(q) \right) + \frac{1}{12N} \left( 1 + \nabla^2_{\iota} S(q) \right)

となり、多項係数の対数値はエントロピーの関数であることが分かった。

pokapoka-jigoku

2について

今後のため、多項係数ではなく多項分布で考える。多項分布は

P = W \prod_i p_i^{k_i} = \frac{N!}{\prod_i k_i!} \prod_i p_i^{k_i}

である。結論からいうと、0となるkを式から除いても結果は変わらない。

\Lambda = \{i | k_i > 0\}

なる集合を考えると、先の式は：

P = \frac{N!}{ \left( \prod_{i \in \Lambda} k_i! \right) \left( \prod_{i \notin \Lambda} k_i! \right) } \left( \prod_{i \in \Lambda} p_i^{k_i} \right) \left( \prod_{i \in \Lambda} p_i^{k_i} \right)

であり、定義より $\forall i \notin \Lambda . k_i = 0$ であるから：

\prod_{i \notin \Lambda} k_i! = 1

\prod_{i \notin \Lambda} p_i^{k_i} = 1

。よって：

P = \frac{N!}{ \prod_{i \in \Lambda} k_i! } \prod_{i \in \Lambda} p_i^{k_i}

である。

以上の結果から、当該の問題を考える際は、対象となる確率分布のうち、実現回数が非ゼロの項目だけに絞って計算してよい。

pokapoka-jigoku

補足）

ただし、当然ながら：

\sum_{i \in \Lambda} p_i < 1

であり、より単純な別の同型な確率問題に読み替えられるわけではないことに注意する。ただし、

\sum_{i \notin \Lambda} p_i = 0

のときは、 $i \in \Lambda$ な項目だけを集めてインデックスを割り振り直すことで、より単純な確率問題に落としこめる（そのようなケースはあまりないかもしれないが）。

pokapoka-jigoku

3.について

今後の宿題とする。一方で、上記の小括の式がそのまま成り立つような気もする。

pokapoka-jigoku

-1. 補遺: 多項分布

せっかくなので多項分布についても求めておこう。多項係数は上述の通りであるから、確率部分だけ計算する。これはこの記事で論じる必要のないぐらい単純な計算で：

\ln \prod_i p_i^{Nq_i} = N \sum q_i \ln p_i = - N S_q(p)

である。ここで $S_q(p)$ はクロスエントロピー。

よって、全体として：

\ln P = - N D_{KL}(q || p) - \frac{r-1}{2} \ln 2\pi N + \frac{1}{2} \left( r + \nabla_{\iota} S(q) \right) + \frac{1}{12N} \left( 1 + \nabla^2_{\iota} S(q) \right)

pokapoka-jigoku

-2. 方向微分項の範囲評価

下記によれば、多項分布の対数値はKL情報量+ $O(\ln N)$ であるとされているが、方向微分項の範囲が確かにそのオーダーに収まるのかどうかを評価したい。

要するに、 $Q_1, Q_2$ の範囲評価である。これらは共通して：

qが一様分布（エントロピー最大）のときに最小／最大
qが最も急峻（エントロピー最小）のときに最大／最小

であることが簡単な計算を通じて分かる（割愛）。

pokapoka-jigoku

$r$ は非ゼロな経験分布の項目数であるので、 $1 \le r \le N$ の制約があることに注意して評価する。

Q_1 = - \sum_i \ln q_i

最小値は、

\min Q_1 = - \sum_i \ln 1/r = r \ln r

最大値は、

\begin{split} \max Q_1 &= - (r-1) \ln (1/N) - \ln \frac{N - r + 1}{N}\\ &= (r-1) \ln N - \ln \frac{N - (r-1)}{N}\\ &= r \ln N - \ln (N - (r-1))\\ \end{split}

pokapoka-jigoku

$N=20$ のときの $\max Q_1,~\min Q_1$

pokapoka-jigoku

Q_2 = 1 - \sum \frac{1}{q_i}

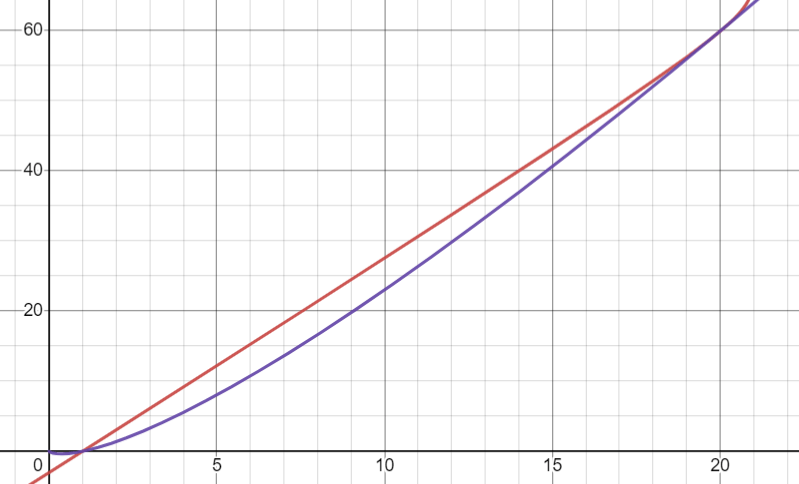
最大値は、qが一様分布のときで

\max Q_2 = 1 - r^2

最小値は、qが最も急峻なときで

\min Q_2 = 1 - (r-1)N -\frac{N}{N-(r-1)}

pokapoka-jigoku

$N=10$ のときの、 $Q_2$ の最大・最小（横軸が $r$ ）

pokapoka-jigoku

上記以上の確実なバウンドを思いつかないので、少々大げさにはなるが、以上の結果を使って範囲を評価する。すなわち、

\frac{1}{2} Q_{1, min} + \frac{1}{12N} Q_{2, min} \le \ln P - \left( - N D_{KL}[q || p] - \frac{r-1}{2} \ln 2\pi N \right) \le \frac{1}{2} Q_{1, max} + \frac{1}{12N} Q_{2, max}

pokapoka-jigoku

下限は：

\frac{r}{2} \ln r + \frac{1}{12N} \left( 1 - (r-1) N - \frac{N}{N-(r-1)} \right) \\ = \frac{r \ln r}{2} - \frac{r-1}{12} \left( 1 + \frac{1}{12N(N-(r-1))} \right)

pokapoka-jigoku

上限は：

\frac{r}{2} \ln N - \frac{1}{2}\ln (N - (r-1)) + \frac{1-r^2}{12N}

pokapoka-jigoku

$\frac{r-1}{N}$ が十分小さい時、

\frac{r-1}{2} \ln N + \frac{r-1}{2N} \left( 1-\frac{r+1}{6} \right)

pokapoka-jigoku

続き