🐢

【統計学】二項分布

2025/06/18に公開

二項分布（Binomial　Distribution）

成功確率 $p$ のベルヌーイ試行を $n$ 回独立に繰り返すとき、成功する回数 $X$ が従う分布。

$X$ ~ $Bin(n,p)$ と表す。

1. 確率関数

$n$ 回の試行のうち成功する回数を $X$ とおくと、確率関数 $f(x)\ge0$ , $\Sigma_xf(x)=1$ は、成功する確率を $p$ として

f(x)=\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}

確率関数の和が1になる証明

\Sigma_xf(x)=\Sigma_x\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}

二項定理より

=(p+(1-p))^n=1^n=1

2. 期待値と分散

期待値： $E[X]=np$

期待値の導出

\begin{align*}&E[X]=\Sigma_xxf(x)\\&=\Sigma_{x=1}^nx\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}\\&=\Sigma_{x=1}^nnp\frac{(n-1)!}{(x-1)!((n-1)-(x-1))!)}p^{(x-1)}(1-p)^{(n-1)-(x-1)}\\&=np\Sigma_{y=1}^{n-1}\frac{(n-1)!}{y!((n-1)-y)!}p^y(1-p)^{(n-1)-y}\\&=np(p+(1-p))^{(n-1)}=np\cdot1^{(n-1)}=np\end{align*}

分散： $V[X]=np(1-p)$

分散の導出

V[X]=E[(X-E[X])(X-E[X])]=E[X^2]-(E[X])^2

ここで

\begin{align*}&E[X^2]=\Sigma_xx^2f(x)\\&=\Sigma_{x=1}^nx^2\frac{n!}{x!(n-x)!}p^x(1-p)^{(n-x)}\\&=\Sigma_{x=1}^n[x(x-1)+x]\frac{n!}{x!(n-x)!}p^x(1-p)^{(n-x)}\\&=\Sigma_{x=1}^nx(x-1)\frac{n!}{x!(n-x)!}p^x(1-p)^{(n-x)}+E[X]\end{align*}

右辺第1項

\begin{align*}&\Sigma_{x=1}^nx(x-1)\frac{n!}{x!(n-x)!}p^x(1-p)^{(n-x)}\\&=\Sigma_{x=2}^nx(x-1)\frac{n!}{x!(n-x)!}p^x(1-p)^{(n-x)}\\&=\Sigma_{x=2}^n\frac{n!}{(x-2)!(n-x)!}p^x(1-p)^{(n-x)}\\&=n(n-1)p^2\Sigma_{x=2}^n\frac{(n-2)!}{(x-2)!((n-2)-(x-2))!}p^{(x-2)}(1-p)^{(n-2)-(x-2)}\\&=n(n-1)p^2\Sigma_{y=0}^{(n-2)}\frac{(n-2)!}{(y!((n-2)-y)!}p^y(1-p)^{(n-2)-y}\\&=n(n-1)p^21^{(n-2)}=n(n-1)p^2\end{align*}

よって

\begin{align*}&V[X]=E[X^2]-(E[X])^2\\&=n(n-1)p^2+np-(np)^2\\&=-np^2+np\\&=np(1-p)\end{align*}

3. 近似

二項分布で試行回数 $n$ が大きいとき、１回の試行の成功確率 $p$ が小さくないならば正規近似、非常に小さいならばポアソン近似が適用できる。

1. 二項分布の正規近似

中心極限定理より、 $n$ が十分大きいとき、二項分布は正規分布で近似できる。
成功回数 $X$ を正規化した変数 $(X-np)/\sqrt{np(1-p)}$ の分布は $n\to\infty$ のとき、平均値0,標準偏差1の正規分布に近づく。

成功の割合

実際の利用場面では成功回数よりも成功の割合を用いることのほうが多い。

例：ある集団の退会者数よりも退会申請率に注目するなど。

変数 $(X-np)/\sqrt{np(1-p)}$ の分子と分母をそれぞれ $n$ で割ると $(X/n-p)/\sqrt{p(1-p)/n}$ 。
よって成功の割合 $X/n$ を正規化した変数 $(X/n-p)/\sqrt{p(1-p)/n}$ の分布は $n\to\infty$ のとき、平均値0,標準偏差1の正規分布に近づく。

例：ある集団の人数 $n$ が $100$ 、退会申請率 $p$ が $6$ %のとき、 $np>5$ より正規近似が適用できる。
退会申請率の95%信頼区間は $p\pm1.96(X/n-p)/\sqrt{p(1-p)/n}$ で求められる。

2. 二項分布のポアソン近似

試行の数 $n$ が大きく、成功確率 $p$ が非常に小さい二項分布はポアソン分布で近似できる。（ $n$ が大きいと二項分布の計算は大変なので、近似を利用する。）

ポアソン分布の詳細は以下の記事を参照。

4. 実務での利用例

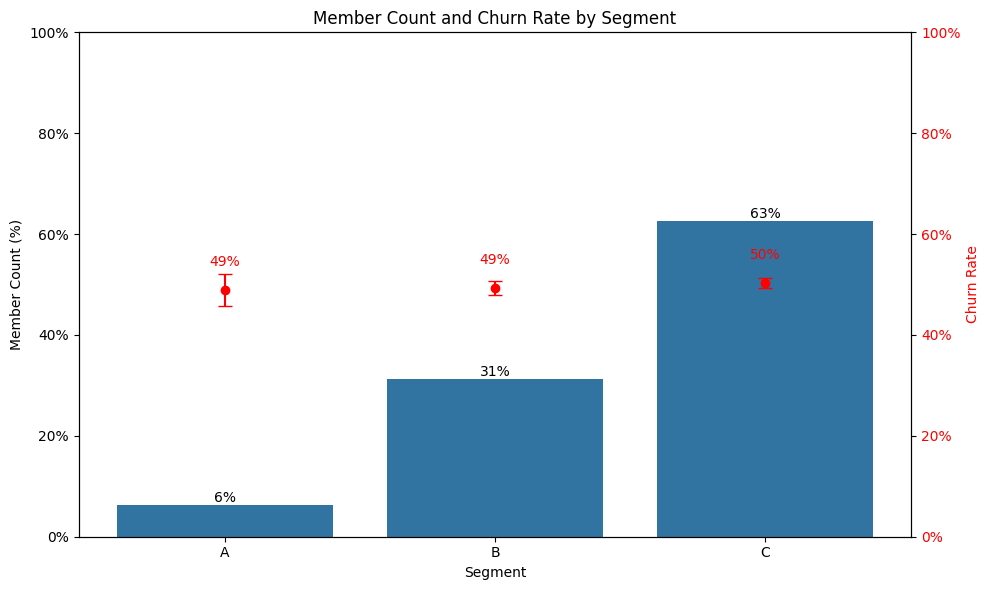
あるサブスクリプションサービスを利用している会員の複数のセグメント間での退会率の比較コード例。

compare_churn_rate.py

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 1. A,B,Cの3つのセグメントに分かれたデータを各セグメントの数を指定して作成

## 1. セグメントごとのデータ数を指定
n_a = 1000
n_b = 5000
n_c = 10000

n = n_a + n_b + n_c

## 2. 各セグメントのデータを作成
segment_data = ['A'] * n_a + ['B'] * n_b + ['C'] * n_c

## 3. 退会フラグのデータを作成
is_churned = np.random.randint(0, 2, size=n).tolist()

## 4. DataFrameを作成
df = pd.DataFrame({
    'segment': segment_data,
    'is_churned': is_churned
})

# 2. セグメントごとの人数と退会率を計算
agg_data = (
    df.groupby('segment')
    .agg(
        member_count=('segment', 'count'),
        churn_rate=('is_churned', 'mean'),
    )
    .reset_index()
)

# 3. 退会率の95%信頼区間幅を計算（エラーバーの可視化に利用するため、信頼区間の半分の幅を算出）
agg_data['ci'] = 1.96 * np.sqrt(
    agg_data['churn_rate'] * (1 - agg_data['churn_rate']) / agg_data['member_count']
)

# 4. 可視化
fig, ax1 = plt.subplots(figsize=(10, 6))

## 1. 会員数のヒストグラムを描画
sns.countplot(
    x='segment',
    data=df,
    stat ='percent',
    order=agg_data['segment'],
    ax=ax1,
)

ax1.set_xlabel('Segment')
ax1.set_ylim(0, 100)
ax1.set_ylabel('Member Count (%)')
ax1.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'{x:.0f}%'))

### 1. 会員数のラベルを追加
for p in ax1.patches:
    ax1.annotate(
        f'{p.get_height():.0f}%',
        (p.get_x() + p.get_width() / 2., p.get_height()),
        ha='center',
        va='bottom',
        fontsize=10,
    )

## 2. 退会率をエラーバー付きでプロット
ax2 = ax1.twinx()

### 1. 退会率の平均値をプロット
ax2.plot(
    'segment',
    'churn_rate',
    data=agg_data,
    marker='o',
    linestyle='',
    color='red',
)

### 2. エラーバーを追加
ax2.errorbar(
    x=agg_data['segment'],
    y=agg_data['churn_rate'],
    yerr=agg_data['ci'],
    fmt='none',
    color='red',
    capsize=5,
)

ax2.set_ylim(0, 1)
ax2.set_ylabel('Churn Rate', color='red')
ax2.tick_params(axis='y', labelcolor='red')
ax2.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'{x*100:.0f}%'))

### 3. 退会率のラベルを追加
for i, row in agg_data.iterrows():
    ax2.annotate(
        f'{row["churn_rate"] * 100:.0f}%',
        (row['segment'], row['churn_rate']),
        ha='center',
        va='bottom',
        fontsize=10,
        color='red',
        xytext=(0, 15),  # 上に少しずらす
        textcoords='offset points'
    )

ax1.set_title('Member Count and Churn Rate by Segment')
plt.tight_layout()
plt.show()

出力結果

脚注

P.G.ホーエル入門数理統計学（p.81） ↩︎
P.G.ホーエル入門数理統計学（p.64） ↩︎