熱力学関数のすべて

まえがき

エントロピー原理からはじめ、教科書的な熱力学関数を2つの系列に分類して動機づけることを考える。熱力学関数はいろいろあるが、その関係は一見単純なようでこまかい符号や係数の違い、用途の違いがある。自分の理解では、熱力学関数は2つの系列できれいに尽きていて(エンタルピー以外)、そのうち1つの系列の関数群が多くの教科書から無視されているために、逆に整理しづらくなっている、というものだ。以前このあたりの話を、Lieb-Yngvason流のエントロピーの定式化からはじめてザッと述べるノートを書いたが、本稿はその後半の書き直しだ。エントロピーの話は本稿では省略し、とにかくエントロピーの性質さえ受け入れられれば準備としてはよいことにする。

エントロピー原理と平衡操作

まずエントロピーについて確認しよう。

エントロピーとは、個々の熱力学系ごとに定められる、マクロ示量変数の有限組を引数とした1次同次上凸の増加関数で、複合系などの系の並列に対しては加法的に拡張される。通常$S$で書く。熱力学のノーテーションは伝統的に破滅していて厳しい気持ちだが、慣習にしたがって察してほしい。以下では、マクロ示量変数は複数まとめて$X,Y$のように書いてしまうが、分けたい時は適当にタプル記法で分割する。

さて、エントロピー原理とは

$$X \rightarrow Y \text{が可能} \Leftrightarrow S(X)\le S(Y)$$

というものだ。ただ、これを愚直に受け止めると、例えば無から示量変数を生成するようなちょっと変な操作もできてしまうことになるので、ノートではこれを緩めたバージョンを宣言した。しかし本稿ではそういうのはあまり気にしないことにする。エントロピーが非減少であれば、すくなくとも"熱力学は"その操作を妨げない。

操作の中で一つ重要なのが、平衡操作 だ。共通の型をもつ示量変数を保存的に開放する。そうすると色んな状態を取ることができるが、「保存則を満たす範囲で全エントロピーが最大」というそれ以上操作できない状態に持っていく操作が平衡操作だ。例えば、$Z$という共通示量変数をもつ2系であれば、$S_1(X,Z_1),S_2(Y,Z_2)$がそれぞれの系のエントロピーだとして、

$$(X,Z_1),(Y,Z_2) \rightarrow (X,Z_1^\star),(Y,Z_2^\star)\\ (Z_1^\star, Z_2^\star) = \mathrm{argmax}_{Z_1^\prime + Z_2^\prime = Z_1 + Z_2}S_1(X,Z_1^\prime) + S_2(Y,Z_1^\prime)$$

というのが常に可能だとする。平衡操作を行ったとき、終状態がどうなるかは、エントロピーに関して開放している変数に関する偏微分で方程式を立てることができる。つまり、

$$\frac{\partial S_1}{\partial Z}(X,Z_1^\star) = \frac{\partial S_2}{\partial Z}(Y,Z_2^\star)$$

だ。エントロピーの偏微分係数は、それが一致することが平衡の必要条件である という特別な意味をもつ。エントロピーについて、その偏微分を、微分変数のエントロピーに関する共役示強変数と呼ぶことにする。共役示強変数を、$B$に添え字して書くことにする。(これは、ボルツマン定数抜きの逆温度を意識している)

示強変数、というのはもちろん次の意味だ。つまり、示量変数を一斉に体数倍しても、変化がない。

$$\frac{\partial S}{\partial X}(\lambda X) = \frac{\partial S}{\partial X}(X)$$

リザバーの定式化

エントロピー$S(X,Y)$を持つ系と、エントロピー$S_R(X)$を持つ系を考えよう。$S_R$側は、スケール因子$\lambda$で大きくしていくことを考え、$X$の全系のトータルを$\lambda X_t$と置こう。この2系が$X$を開放して平衡しているなら、そのエントロピーは

$$\max_{X} S(X,Y) + S_R(\lambda X_t - X)$$

である。ところで、$S_R$が滑らかだとするとエントロピーの1次同次性から

$$= \max_{X} S(X,Y) + \lambda S_R\left(X_t - \frac{X}{\lambda}\right)\\ = \max_{X} S(X,Y) + \lambda S_R(X_t) - \frac{\partial S_R}{\partial X}(X_t)X + \Omicron(\lambda^{-1})$$

となる。また、$S_R$がもう一段滑らかで、$\lambda$が十分大きいときは

$$\frac{\partial S_R}{\partial X}(\lambda X_t - X) = \frac{\partial S_R}{\partial X}(X_t) + \Omicron(\lambda^{-1})$$

共役示強変数は$X$に対してほとんど変化しなくなり、その値は$\frac{\partial S_R}{\partial X}(X_t)$である。

これは何を意味するのだろうか？ まず後者は、系をどんどん大きくしていった極限に対応する系として、エントロピーの共役示強変数が定数になるような系を考えることができる。これが、リザバー である。リザバーは現実にはフィードバック制御された恒温槽のようなものだが、そのポイントは示強変数を外部から与えて一定にできるということだ。示強変数を固定できる、ということは、リザバーと平衡している系の示強変数もまた固定される。つまり、リザバーを適切に設定して使うことで、系を示強変数を使って操作することができる。

どのような系であっても、示量変数を無限にスケールさせる操作をすれば、漸近的にリザバーとして振る舞わせることができるが、今リザバーの性質として共役示強変数が定数という理解を得たので、これを直接定義しておくのがよい。つまり、リザバーとは、定数である共役示強変数で特徴づけられ、エントロピーが示量変数の1次関数であるような系のことである。

平衡の効用関数

先の計算をもう一度書くと、巨大($\lambda \gg 1$)な系と接触している$S(X,Y)$のエントロピーは

$$\max_{X} S(X,Y) + \lambda S_R(X_t) - \frac{\partial S_R}{\partial X}(X_t)X + \Omicron(\lambda^{-1})$$

となるのだった。$S_R$がリザバーであるなら、$\frac{\partial S_R}{\partial X}(X_t)$は、それを特徴づける共役示強変数で定数である。定数である$X_t,\lambda$にしか依存しない項を無視し、$\frac{\partial S_R}{\partial X}(X_t) = B$とすると、

$$\max_{X} S(X,Y) - BX$$

となり、これは部分ルジャンドル変換になっている。これは、リザバーと接触している系の実効的なエントロピー関数は、そのルジャンドル変換であることを意味する。実効的な、という修辞の意味は、エントロピー関数を「平衡操作における最大化目的関数とみなすときに」という意味だ。平衡操作ではエントロピーは最大化される。逆に、「平衡操作のときに、それを最大化すればよいような量」を実効的なエントロピーと呼んでいる。例えば、今リザバー付きの系は、まだ$Y$という変数を持っている。そこで、エントロピー$S^\prime(Y)$をもつ別の系と$Y$を開放して平衡させる場合、その全エントロピーの計算では、$S(X,Y)$を使うのではなくて、$\max_{X} S(X,Y) - BX$を使わなくてはならない、ということだ。

このようなものを総称する名前がないのだが、個人的にはutilityと呼んでいる。これは熱力学を模倣した経済学の均衡理論における「効用」という言葉の逆輸入だ。ともかく、名称はどうでもよくて、utilitiesとは、エントロピーに対する部分ルジャンドル変換のこととしよう。そしてその解釈は、平衡条件を求めるための実効的エントロピーということだ。

ただ、これ以降の話との対応をもたせるために、ちょっと制限をする。今までの話では、示量変数の内容について何も制限をしていなかった。実際、なんでもいい。しかし次節以降は、ある示量変数を特別視する。なので、エントロピーの段階で、示量変数一つを特別扱いしておこう。これは、エネルギーと呼ぶが、形式論としては必ずしもエネルギーでなくてもよい。

これ以降、エントロピーは

$$S(U,X)$$

のように、第一引数をエネルギー$U$として特等席を設ける。共役示強変数も、$U$の共役は添字無しの$B$、それ以外は添字なりの修飾を設けることにする。例えば、$U,X_1,X_2\dots$の共役示強変数が$B,B_1,B_2\dots$で固定されたリザバーのエントロピーは

$$S_R(U,X_1,X_2\dots) = BU + B_1X_1 +B_2X_2 \dots$$

という具合だ。また、部分ルジャンドル変換を行うとき、$U$は必ず変換対象に含めることにする 。これはエネルギーを開放せずに、他の示量変数だけを開放する、という状況がちょっと考えにくいからだ。$U$以外の変数を、$X = (\overline{X},\underline{X})$のように2グループに分けると、utilitiesとは、エントロピー$S(U,X)$及び、次のようなルジャンドル変換たち、ということになる。

$$\Phi(B,\overline{B},\underline{X}) = \max_{U,\overline{X}} S(U,\overline{X},\underline{X}) - BU - \overline{B}\cdot \overline{X}$$

自由エネルギー関数

熱力学系は、大量の微視的な自由度を持つが、それをごく僅かなマクロ変数だけで制御しようとしている。これはもちろん不可能で、エントロピーによって可能な操作が制限されている。このため、示量変数を熱力学系に投入してしまうと、それはただでは取り出すことができない。では、具体的な操作を行って熱力学系から示量変数を取り出そうとする時、どこまでそれが可能だろうか？

ここで考えたいことは、つまりこういうことだ。「熱力学系を操作することで、ある示量変数を、どこまで減らすことができるか？」 なぜ減らすかというと、示量変数は外系と保存則を満たしているので、系の示量変数を減らせれば、それは外に取り出せたことになるからだ。

ここでは、取り出そうとしている示量変数を、エネルギーとする。つまり、前節で固定した$S$の第一引数$U$だ。もちろん、これは便宜的なものなので、形式論としては何でも良い。そして、ある操作における、系のエネルギー$U$の減少幅を、仕事と呼び、$W$に添え字して表す。

まず、補題を示しておく。

補題 エントロピーを変化させない操作は、最大仕事をなす。より正確には、同じ示量変数状態から開始し、エネルギー以外の終了状態が同じであるような操作のうち、もっともエネルギーを減少させるのは、エントロピーを変化させない操作である。

証明は次のようになる。$(U_1,X_1)\rightarrow (U_2,X_2)$がエントロピーを変化させないとする。つまり$S(U_1,X_1) = S(U_2,X_2)$だ。エントロピー原理から、逆操作$(U_2,X_2)\rightarrow (U_1,X_1)$が可能である。この逆操作のあとに、任意の操作$(U_1,X_1)\rightarrow (U_3,X_2),S(U_1,X_1)\le S(U_3,X_2)$を続けることが可能だが、これは可能なので$S(U_2,X_2) \le S(U_3,X_2)$である。エントロピーはエネルギーの単調関数だから、$U_2 \le U_3$でなくてはならない。とくにそれぞれの操作の仕事に換算すると、$U_1 - U_2 \ge U_1 - U_3$である。したがって、エントロピーを変化させない操作は最大仕事を成す。

今最大化したいのがエネルギーの変化なので、エントロピー関数を逆に解いておく。つまり、これからは$S(U,X)$に対応するものとして、その陰関数$U(S,X)$を考えていく。エントロピーはエネルギーの単調関数だから、これは解くことができる。

さて、「系からエネルギーをどれだけ取り出せるか？」を考えよう、まず仕事について

$$W_{\max X \rightarrow Y}$$

という記法で、$X \rightarrow Y$という操作での最大仕事を表すとしよう。ここで、注意として、$X,Y$は、示量変数すべてを表さないことがある。 その場合は「示された示量変数について、それを開始/終了状態として持つような操作のうちで、最大仕事」と読むことにする。なぜこうするかというと、あとでリザバーを使って、一部の変数を示強変数を通じて暗黙に制御するからだ。

さて、リザバーを一切用いない場合、最大仕事はとても簡単だ。補題が示す通り、それはエントロピーを変えないような操作だから、$S=S(U_0,X_0)$として、

$$W_{\max (U_0,X_0)\rightarrow (U_1,X_1)} = U(S,X_0) - U(S,X_1)$$

である。興味深いのは、リザバーを使う場合だ。ここでも、リザバーは、少なくとも$U$を供給するとしよう。$X=(\overline{X},\underline{X})$とし、$U,\overline{X}$について、それぞれ共役示強変数$B,\overline{B}$で供給するリザバーを考える。そのようなリザバーのエントロピー関数は

$$S_R(U,\overline{X}) = BU + \overline{B}\cdot\overline{X}$$

だから、逆に解くと

$$U_R(S,\overline{X}) = B^{-1}S - B^{-1}\overline{B}\cdot \overline{X}$$

である。リザバーがエネルギーを供給する可能性があるのだから、仕事を考えるときは、リザバーを一緒に考える必要がある。系の初期状態エントロピーを$S_0$、初期状態を$X_0$、全系エントロピーを$S_t$、全系のリザバー供給示量変数を$\overline{X}_t$としよう。初期状態の全エネルギーは

$$U(S_0,\overline{X}_0,\underline{X}_0) + U_R(S_t-S_0,\overline{X}_t - \overline{X}_0)$$

となる。エントロピーを減少させない操作が最大仕事をなすという性質は、複合系でも成り立つから、全エントロピーは保存させた状態で、リザバーが供給する変数である$S_1,\overline{X}_1$の終了状態について次の最大値を探索すればよいことになる。

$$\begin{align*} &W_{\max \underline{X}_0 \rightarrow \underline{X}_1} \\ =& \max_{S_1,\overline{X}_1} U(S_0,\overline{X}_0,\underline{X}_0) + U_R(S_t-S_0,\overline{X}_t - \overline{X}_0) - U(S_1,\overline{X}_1,\underline{X}_1) - U_R(S_t-S_1,\overline{X}_t - \overline{X}_1) \end{align*}$$

リザバーのエネルギー関数を代入して計算すると

$$\begin{align*} & \max_{S_1,\overline{X}_1} U(S_0,\overline{X}_0,\underline{X}_0) + U_R(S_t-S_0,\overline{X}_t - \overline{X}_0) - U(S_1,\overline{X}_1,\underline{X}_1) - U_R(S_t-S_1,\overline{X}_t - \overline{X}_1) \\ = & U(S_0,\overline{X}_0,\underline{X}_0)- B^{-1}S_0 + B^{-1}\overline{B}\cdot \overline{X}_0 \\ - & \min_{S_1,\overline{X}_1}\left[ U(S_1,\overline{X}_1,\underline{X}_1)- B^{-1}S_1 + B^{-1}\overline{B}\cdot \overline{X}_1 \right] \end{align*}$$

ここまでは$W_{\max X\rightarrow Y}$という形で、リザバーが制御していない示量変数についての開始・終了条件を固定して最大仕事を考えた。ところが、これは片方だけを考えてもよい。

補題 $W_{\max X\rightarrow Y} = - W_{\max Z\rightarrow X} + W_{\max Z\rightarrow Y}$

次のように考える。最大仕事はいずれも(リザバーがあるときはそれを含めた)エントロピーを変えない操作で実現していた。これは可逆であり、そのとき逆操作の仕事は符号を変えたものであって、それもまた最大仕事である。つまり、$W_{\max X\rightarrow Y}= - W_{\max Y\rightarrow X}$となる。$X\rightarrow Z$と$Z\rightarrow Y$で$Z$を中継しつつそれぞれ最大仕事操作(等エントロピー)をする場合も、$X\rightarrow Y$での最大仕事を実現する操作のうち一つなので、$W_{\max X\rightarrow Y} = W_{\max X\rightarrow Z} + W_{\max Z\rightarrow Y}$が成り立つ。

そうすると、「最大仕事を計算するときは、常に操作の前後状態での差を計算する」という約束のもとで、終了状態に依存する部分だけを取り出してよいことになる。そこで、

$$\min_{S_1,\overline{X}_1} U(S_1,\overline{X}_1,\underline{X}_1)- B^{-1}S_1 + B^{-1}\overline{B}\cdot \overline{X}_1$$

にだけ着目しよう。これはやはりルジャンドル変換になっているが、少し変数が汚い。そこで、

$$B^{-1} = T\\ B^{-1}\overline{B} = \overline{P}$$

という記号の約束をして、

$$F(T,\overline{P},\underline{X}) = \min_{S,\overline{X}} U(S,\overline{X},\underline{X})- TS + \overline{P}\cdot \overline{X}$$

と定め、これを一切ルジャンドル変換をしない$U(S,X)$とともに、free energyと呼ぶ。

free energyの解釈はその差が系から取り出せる最大のエネルギー になる、というものだ。つまり

$$W_{\max \underline{X}_0\rightarrow \underline{X}_1} = F(T,\overline{P},\underline{X}_0) - F(T,\overline{P},\underline{X}_1)$$

ミッシングリンク

細々とした議論をしてきたが、ここまでで用いられているアイデアは本質的に3つしかない。

• リザバーの性質を同定して明示的に扱う
• $U,X$を保存させ、全系の終了状態エントロピーを最大化する(平衡させるため)
• $S,X$を保存させ、全系の終了状態エネルギーを最小化する(仕事させるため)

その結果utilitiesが、$S(U,X)$および、

$$\Phi(B,\overline{B},\underline{X}) = \max_{U,\overline{X}} S(U,\overline{X},\underline{X}) - BU - \overline{B}\cdot \overline{X}$$

またfree enegryが、$U(S,X)$および、

$$F(T,\overline{P},\underline{X}) = \min_{S,\overline{X}} U(S,\overline{X},\underline{X})- TS + \overline{P}\cdot \overline{X}$$

としてその解釈と共に定まる。これらはともに、$X=(\overline{X},\underline{X})$の選び方だけ存在するが、すべての変数をルジャンドル変換すると、$S,U$は一次同次関数であるために系のアイデンティティがなくなってしまうこと、また今$U$を特別視していることから、$n$変数(うちひとつがエネルギー)の熱力学関数は、$2 \times (1+(2^{(n-1)}-1)) = 2^n$個あることになる。

ところが、これらの間には$B^{-1} = T, B^{-1}\overline{B}=\overline{P}$のもとで次の対応がある。

$$\begin{align*} &\Phi(B,\overline{B},\underline{X})\\ =& \max_{U,\overline{X}} S(U,\overline{X},\underline{X}) - BU - \overline{B}\cdot \overline{X}\\ =& \max_{S,\overline{X}} S - BU(S,\overline{X},\underline{X}) - B\overline{P}\cdot \overline{X}\\ =& -B\min_{S,\overline{X}}\left[ U(S,\overline{X},\underline{X}) - TS + \overline{P}\cdot \overline{X} \right]\\ =& -BF(T,\overline{P},\underline{X}) \end{align*}$$

つまり、たかだか$T(B)$倍の違いしかない。このせいでutilitiesの方は知名度が低い。$S$以外のutilitiesを無視すると、熱力学関数は$1 + 2^{n-1}$個に減ってしまう。

実はutilitiesの知名度が低いことが、熱力学関数をきれいに列挙することの障害になっていた。

例えば、次のように思ったことは無いだろうか？

• 統計力学を考えるとき、分配関数から熱力学関数・示強変数を計算するとき、$T$がかかったりかからなかったりするのはなぜだろうか？
• エントロピーと自由エネルギーの間を行き来するときに、$T$がかかったりかからなかったりするのはなぜだろうか？
• ルジャンドル変換をするときに、ある符号はプラスである符号はマイナスにするのはなぜだろうか？

それはいずれも、熱力学関数がこのように2系列に分裂していたことを無視していたからだったのだ。分配関数から直接結びつくのは、実はfree energyではなくutilitiesの方だ。utilitiesの方に対応させれば、逆温度で割る必要はない。

free energyのルジャンドル変換をするときに、導入する変数の符号が違うのも、エネルギーを特別扱いしたうえで、リザバーのエントロピーをエネルギーについて逆に解いているからだ。熱力学関数の各種公式で符号がついたりつかなかったり、$T$がかかったりかからなかったりするのは、それが暗にutilitiesとfree energyをまたぐ計算を行っていたからだ。

$U,V,N$変数の場合の例

標準的な3変数熱力学で具体的な熱力学関数を列挙する。ここで忘れ去られていたutilitiesたちが、マシュー関数、プランク関数、クラマース関数だ。エントロピー、エネルギーから始めて、マシュー関数、プランク関数、クラマース関数、ヘルムホルツ自由エネルギー、ギブス自由エネルギー、グランドポテンシャルの8個を定義することで、教科書に出てくるよくある熱力学関数を概ねカバーできる。

変数の対応をつけておこう。これまでの一般論の$(U,X)$が$(U,V,N)$に対応する。これに対応してエントロピーにおける共役示強変数$B,B_V,B_N$があるが、Wikipediaと太田先生の本に倣って$B,\Pi,\alpha$と置くことにする。

free energyの共役示強変数は

$$\begin{align*} T&=B^{-1}\\ p&=P_V=B^{-1}B_V=B^{-1}\Pi\\ -\mu&=P_N=B^{-1}B_N=B^{-1}\alpha \end{align*}$$

となるが、これは温度、圧力、化学ポテンシャルと呼ばれている(化学ポテンシャルの符号は後述)。

utilites

ここで大変残念なお知らせがある。utilitiesはマイナーであるためか、記号の互換性が無い。 自分のノートや記事の間ですら互換性がない。どうか皆さんでベストな記号を選んでほしい。クラマース関数は、Wikipediaでは$q$になっていたのでこの記事ではそれに倣った。

• $S(U,V,N)$：エントロピー
• $\Psi(B,V,N) = \max_{U} S(U,V,N) - BU$：マシュー関数
• $\Phi(B,\Pi,N) = \max_{U,V} S(U,V,N) - BU - \Pi V$：プランク関数
• $q(B,V,\alpha) = \max_{U,N} S(U,V,N) - BU - \alpha N$：クラマース関数

free energy

ここでももう一つ残念なお知らせがある。それは物質量$N$の共役変数の符号だ。一般論の定義では、$N$に対応する$B^{-1}B_N$がそれになるはずだが、歴史的経緯によって、化学ポテンシャル$\mu$の符号は逆になっている。これが「逆」であることは次のように考えればわかる。例えば、圧力は、$V$が増加したときに、系から失われるエネルギーだ。しかし、化学ポテンシャルは$N$が増加したときに、系が獲得するエネルギーなので、ここだけ符号が逆になる。歴史的経緯からは何者も逃れられないので、慣れるしかない。

• $U(S,V,N)$：エネルギー
• $F(T,V,N) = \min_{S} U(S,V,N) - TS$：ヘルムホルツ自由エネルギー
• $G(T,p,N) = \min_{S,V} U(S,V,N) - TS + pV$：ギブス自由エネルギー
• $J(T,V,\mu) = \min_{S,N} U(S,V,N) - TS - \mu N$：グランドポテンシャル

対応

もちろん一般論で見たようにこれらは対応していて、

• $B^{-1} = T$
• $B^{-1}\Pi = p$
• $B^{-1}\alpha = -\mu$

の約束のもとで

• $\Psi(B,V,N) = -BF(T,V,N)$
• $\Phi(B,\Pi,N) = -BG(T,p,N)$
• $q(B,V,\alpha) = -BJ(T,V,\mu)$

が成り立つ。

統計力学との関連

さらに畳み掛けるようで申し訳ないが、やはり残念なお知らせがある。統計力学の各種アンサンブルは、free energyよりはutilitiesに結びつくのだが、またしてもutilitiesの知名度が低いがために、普通の教科書ではアンサンブルの引数は皆free energy系列のそれをとるのが習慣になってしまっている。しかも中途半端に。

• $S(U,V,N) = k_B\log W(U,V,N)$：ミクロカノニカル
• $\Psi(B,V,N) = k_B\log Z(\beta = k_B^{-1}B,V,N)$：カノニカル
• $\Phi(B,\Pi,N) = k_B\log \Delta(\beta = k_B^{-1}B,p = B^{-1}\Pi,N)$：等温等圧
• $q(B,V,\alpha) = k_B\log \Xi(\beta = k_B^{-1}B,V,\mu = -B^{-1}\alpha)$：グランドカノニカル

逆温度だけ歩み寄っているが、ボルツマン定数が巻き込まれているので微妙に一致しない。

というわけで、残念ながら当面の間はこれまでに成立した習慣も同時に身に付けるしかなさそうである。

熱力学関数の世界

統計力学との関連を考慮して、すべての熱力学関数をレイアウトするとすれば、以下のようになる。$U,S$またはミクロカノニカルから全ての熱力学関数と分配関数が派生する。それぞれの平面では、ルジャンドル変換によって移り合う(分配関数の場合は$\int \exp(-BU/k_B)$)。垂直の対応は$k_B\log$または$-T$倍によって成され、基本的には2つの要素の間をどの経路を経て計算してもよい。

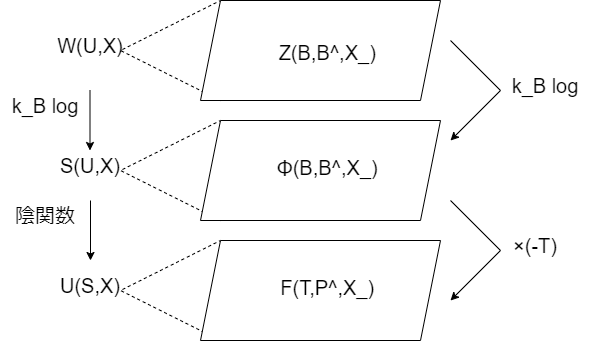
熱力学関数を整理するための他の方法としては、ボルンの四角形がある。これは端正ではあるが、実質的には$U(S,V,N)$からのルジャンドル変換の一覧であり、エントロピー$S(U,V,N)$は含まれていないという欠点がある。

実を言うと、utilities系列を知らなかった時期は、$S(U,V,N)$からのルジャンドル変換で$F,G,J$が得られると考えていた。しかしその場合は随所での$T$倍の食い違いが説明できないし、統計力学とのかみ合いも悪くなる。なんとかしてすべての熱力学関数を動機づけられないのか、と思っていたところ、太田先生の本でマシュー/プランク関数の存在を知った。これがミッシングリンクであった。最終的に、各熱力学関数の解釈を尊重しつつすべてを列挙するには、2つの系列を区別して動機づける必要があるという理解に至った。この記事の方法ではエンタルピー$H=U+pV$が出てこないが、エンタルピーの動機づけはutilitiesでもfree energyでもない別のなにかだろうと考えている。