調和振動子とフーリエ変換

いわゆるスクイズ変換とユニタリな線形正準変換について。

量子的調和振動子

無次元化された量子的調和振動子の基本的事実を確認する。ハミルトニアンは

$$H = \frac{1}{2}P^2 + \frac{1}{2}X^2$$

で、$L^2(\mathbb{R})$上で表現したときは、$X$は掛け算作用素、$P$は$\frac{1}{i}\frac{\partial}{\partial x}$である。ハミルトニアンのスペクトルは離散的で$n+\frac{1}{2},n\in \mathbb{N}$である。固有ベクトルも$n$に従って列挙でき、エルミート多項式$H_n(x)$を使って

$$\phi_n(x) = \langle x | n \rangle= \frac{1}{\pi^{\frac{1}{4}}\sqrt{n!2^n}}H_n(x)\exp\left(-\frac{1}{2}x^2\right)$$

となるが、このことは後半まで使わないのでおいておく。これは一般的な「粒子」描像(ボソンフォック空間)のプロトタイプとしても用いられ、そこでは次のラダーオペレータが使われる。

$$a = \frac{1}{\sqrt{2}}(X+iP)\\ a^\dagger = \frac{1}{\sqrt{2}}(X-iP)\\ [a,a^\dagger] = 1$$

このときは

$$H = a^\dagger a + \frac{1}{2}$$

で、基底状態$\ket{0}$は$a\ket{0} =0$の唯一解となる。

スクイズ変換

一般のボソンフォックでも議論できるが、ラダーオペレータの線形変換となるようなボソンフォック空間のユニタリをボゴリューボフ変換、とくに1モードボソンフォック空間( = 量子的調和振動子)のときのそれをスクイズ変換という。つまり、今の状況では

$$UaU^\dagger = xa + ya^\dagger$$

となるような$U$のことだ。これの成す群を$\mathrm{Sq}$としよう。$UaU^\dagger$は再び正準交換関係を満たすことから

$$[xa + ya^\dagger,x^* a^\dagger + y^* a] = |x|^2 - |y|^2 = 1$$

となる。これをラダーオペレータではなく$X,P$への作用として書くと

$$\begin{align*} U \begin{bmatrix} X\\ P \end{bmatrix} U^\dagger = \begin{bmatrix} \mathrm{Re}x + \mathrm{Re}y, -\mathrm{Im} x +\mathrm{Im}y\\ \mathrm{Im} x +\mathrm{Im}y, \mathrm{Re}x - \mathrm{Re}y \end{bmatrix} \begin{bmatrix} X\\ P \end{bmatrix} \end{align*}$$

となり、係数行列を

$$\begin{align*} M_{U^{-1}} = \begin{bmatrix} \mathrm{Re}x + \mathrm{Re}y, -\mathrm{Im} x +\mathrm{Im}y\\ \mathrm{Im} x +\mathrm{Im}y, \mathrm{Re}x - \mathrm{Re}y \end{bmatrix} \end{align*}$$

とするとこれは$SL(2,\mathbb{R})$の元である。ここから、いまスクイズ群と特殊線形群の間に、$\mathrm{Sq}\rightarrow SL(2,\mathbb{R})_{op}$という"反変"準同型があることになる。この$\ker$がまだ謎だがそれは実質$U(1)$なことが後でわかる。反変なのは、

$$\begin{align*} VU \begin{bmatrix} X\\ P \end{bmatrix} U^\dagger V^\dagger = M_{U^{-1}}M_{V^{-1}} \begin{bmatrix} X\\ P \end{bmatrix} \end{align*}$$

となって、結合順序が逆になるからだ。したがって一方を"逆群"とみたときに通常の準同型になる。そのために$M_{*}$の記号にあらかじめ$-1$を入れておいた。

$SL(2,\mathbb{R})$について調べよう。この群を微分すれば次がリー代数の基底になることがすぐわかる。

$$\begin{align*} \sigma_+ &= \begin{bmatrix} 1,0\\ 0,-1 \end{bmatrix}\\ \sigma_\times &= \begin{bmatrix} 0,1\\ 1,0 \end{bmatrix}\\ \sigma_r &= \begin{bmatrix} 0,-1\\ 1,0 \end{bmatrix} \end{align*}$$

それぞれの添字は、具体的にこの指数写像を計算したとき振る舞いからくる。

$$\begin{align*} \exp(r\sigma_+) &= \begin{bmatrix} e^r,0\\ 0,e^{-r} \end{bmatrix}\\ \exp(r\sigma_\times) &= \begin{bmatrix} \cosh(r),\sinh(r)\\ \sinh(r),\cosh(r) \end{bmatrix}\\ \exp(r\sigma_r) &= \begin{bmatrix} \cos(r),-\sin(r)\\ \sin(r),\cos(r) \end{bmatrix} \end{align*}$$

つまり、それぞれ水平鉛直方向の伸縮、斜め方向の伸縮、回転となる。リー代数の括弧関係は

$$\begin{align*} [\sigma_+,\sigma_\times] &= -2\sigma_r\\ [\sigma_+,\sigma_r] &= -2\sigma_\times\\ [\sigma_\times,\sigma_r] &= 2\sigma_+\\ \end{align*}$$

となっている。実は、スクイズ群$\mathrm{Sq}$側にこれに対応するものを用意できる。それはラダーオペレータを使っていて必然的に非有界作用素だが、正準交換関係から次が全く同じ構造定数を持つことがわかる。

$$\begin{align*} A_+ &= \frac{1}{2}(a^2 - a^{\dagger 2})\\ A_\times &= \frac{1}{2i}(a^2 + a^{\dagger 2})\\ A_r &= \frac{1}{2i}(aa^\dagger + a^\dagger a) \end{align*}$$

この作用素の指数写像も計算できる。次の公式を使う。

$$\exp(s)Z\exp(-s) = \sum_{n}\frac{1}{n!}[s,-]^nZ$$

$$\begin{align*} \exp(rA_+)a\exp(-rA_+) &= \cosh(r)a + \sinh(r)a^\dagger\\ \exp(rA_\times)a\exp(-rA_\times) &= \cosh(r)a + i\sinh(r)a^\dagger\\ \exp(rA_r)a\exp(-rA_r) &= \cos(r)a + i\sin(r)a \end{align*}$$

したがって$SL(2,\mathbb{R})$の元として書くなら

$$\begin{align*} M_{\exp(rA_+)^{-1}} &= \begin{bmatrix} e^r,0\\ 0,e^{-r} \end{bmatrix} = \exp(r\sigma_+)\\ M_{\exp(rA_\times)^{-1}} &= \begin{bmatrix} \cosh(r),\sinh(r)\\ \sinh(r),\cosh(r) \end{bmatrix}= \exp(r\sigma_\times)\\ M_{\exp(rA_r)^{-1}} &= \begin{bmatrix} \cos(r),\sin(r)\\ \sin(r),\cos(r) \end{bmatrix} = \exp(r\sigma_r) \end{align*}$$

となり、$A_+\mapsto -\sigma_+,A_\times \mapsto -\sigma_\times,A_r \mapsto -\sigma_r$の対応が、$\mathrm{Sq}\rightarrow SL(2,\mathbb{R})_{op}$の反変準同型からくるリー代数の"反変"準同型の一部であることがわかる。構造定数が同一なままマイナス符号をつけた、つまり普通のリー代数の準同型の$-1$倍になっているが、これが"反変"準同型の意味だ。この像は明らかに$SL(2,\mathbb{R})$を走っており、ラダーオペレータは今考えているヒルベルト空間では稠密である。したがって$\mathrm{Sq}$の残りの自由度はすべての作用素と可換なものしかなく、それは$U(1)$自由度となる。要約すれば、次の反変同型がある。

$$\mathrm{Sq}/U(1) \simeq SL(2,\mathbb{R})_{op}$$

$U(1)$にはそれほど興味がないので、$A_+,A_\times,A_r$の指数写像で得られるスクイズ変換について考えよう。つまり、スクイズ変換群の$SL(2,\mathbb{R})$部分群である。

スクイズ変換の空間作用

$\sigma_+,\sigma_\times,\sigma_r$がそれぞれ水平垂直の伸縮、斜め伸縮、回転であったので、前者の2つはリー代数の元としては独立だが、機能としては被っていることになる。例えば、斜め伸縮は45°回転、水平垂直伸縮、45°回転で代用できる。そこで、$\sigma_+,\sigma_r$だけを考えよう、対応する$A_+,A_r$の具体的な$L^2(\mathbb{R})$への作用を求めたい。

このうち、$A_+$については簡単だ。$t$に対して次の変換を考えてみる。

$$W(t)[f](x) = \sqrt{e^t}f(xe^t)$$

$t$が小さいときは

$$\begin{align*} &W(t)[f](x) \\ = & \left(1+\frac{1}{2}t\right)\left(f(x) + xt\frac{d}{dx}f(x)\right)\\ = & \left(1+t\left(\frac{1}{2} + x\frac{d}{dx}\right)\right)f(x) \\ = & \left(1+t\frac{i}{2}\left(XP + PX\right)\right)f(x) \\ = & \left(1+t\frac{1}{2}\left(a^2 - a^{\dagger 2}\right)\right)f(x) \\ = & \left(1+t A_+\right)f(x) \end{align*}$$

となり、$A_+$は、ユニタリ$W(t)$の生成子である。したがって、$\exp(tA_+) = W(t)$となる。これはウェーブレットのスケーリングと同じ形だ。

一方で$A_r$のほうはすこしむずかしい。ここで量子的調和振動子が効いてくる。実は

$$A_r = -\frac{i}{2}\left( X^2 + P^2 \right)$$

であるため、量子的調和振動子のハミルトニアンであり、この指数写像は量子的調和振動子の時間発展そのものである。ただし、これを積分核で書き下すのは若干面倒だ。要するに時間発展を積分形で書くのだから、調和振動子のグリーン関数がわかればよい。そのものずばりのMehlerの公式があり、それによれば

$$\begin{align*} & \sum_n \frac{z^n}{n!2^n}H_n(x)H_n(y) \\ = & \sqrt{\pi}\sum_n z^n\phi_n(x)\phi_n^*(y) \\ = & \frac{1}{\sqrt{1-z^2}}\exp\left(\frac{2xyz-z^2(x^2+y^2)}{1-z^2}\right) \end{align*}$$

時間発展のグリーン関数とはつまり

$$K(x,y;t)=\sum_n \phi_n(x) \exp\left(-it\left(\frac{1}{2}+n\right)\right) \phi_n^*(y)$$

なのだからMehlerの公式で$z = \exp(-it)$とすれば

$$\begin{align*} &K(x,y;t)\\ = & \sum_n \phi_n(x) \exp\left(-it\left(\frac{1}{2}+n\right)\right) \phi_n^*(y) \\ = & \frac{1}{\sqrt{\pi}}\exp\left(-\frac{it}{2}-\frac{1}{2}(x^2+y^2)\right)\sum_n \frac{(e^{-it})^n}{n!2^n}H_n(x)H_n(y) \\ = & \frac{1}{\sqrt{\pi}}\exp\left(-\frac{it}{2}\right)\frac{1}{\sqrt{1-e^{-2it}}}\exp\left(\frac{xy}{i\sin(t)}+\frac{i(x^2+y^2)}{2\tan(t)}\right)\\ = & \frac{1}{\sqrt{2\pi i\sin(t)}}\exp\left(\frac{xy}{i\sin(t)}+\frac{i(x^2+y^2)}{2\tan(t)}\right) \end{align*}$$

となる。これによる$y$積分を行えば、$A_r$の指数写像となる。

$$\bra{x}\exp(tA_r)\ket{f} = \frac{1}{\sqrt{2\pi i\sin(t)}}\int_\mathbb{R} \exp\left(\frac{xy}{i\sin(t)}+\frac{i(x^2+y^2)}{2\tan(t)}\right) f(y)dy$$

興味深いのは$t=\frac{\pi}{2}$としたときだ。この時は

$$K\left(x,y; \frac{\pi}{2}\right) = \frac{1}{\sqrt{2\pi i}}\exp\left(-ixy\right)$$

となり、位相を除いてノルム保存版のフーリエ変換に帰着する。実際、この積分は任意「角度」のフーリエ変換の一般化になっている。量子的調和振動子の時間発展はX-P平面に擬古典的に表示(ウィグナー関数など)した場合には、原点周りの回転となることが知られているが、あの回転は実は任意「角度」のフーリエ変換だったことになる。例えば、量子的調和振動子の初期状態を適当な波動関数として「入力」し、$\frac{\pi}{2}$秒待つと、そのフーリエ変換が得られている、ということになる。俄然量子的調和振動子が欲しく(?)なってくる。

線形正準変換(LCT)

線形正準変換 というのがあり、これはいくつかの積分変換を一般化したものとされている。具体的には、フーリエ変換、フレネル積分、スケーリングを含む。

線形正準変換の積分核は複雑な形をしており、そのパラメータは$SL(2,\mathbb{C})$を成すという。ところで、$SL(2,\mathbb{C})$ではなく、$SL(2,\mathbb{R})$の部分であれば、ここまでのスクイズ変換群でカバーできている。$SL(2,\mathbb{R})$に属さない部分については、これは$A_+,A_\times,A_r$を複素係数に拡張したものと考えることができるが、ユニタリ性から$SL(2,\mathbb{R})$を導いたので、これはユニタリ性に反していることになる。ユニタリなものに限定すれば、それはちょうど量子的調和振動子のスクイズ変換群=スケーリングと任意角度フーリエ変換だったということだ。

(追記)プロットしてみる

GPT氏にそれらしい実験コードを書いてもらう。量子的調和振動子の固有状態波動関数は、嬉しいことにフーリエ変換に対して自己双対で、つまりフーリエ変換の解析的な式が得られている。これは(本来$L^2(\mathbb{R})$の元ではないものの)$\exp(-ikx)$との内積が厳密にわかっているということと同じだ。したがって、$\exp(-ikx)$を初期状態として量子的調和振動子の時間発展=任意階フーリエ変換の像は、この変換係数を時間発展して再度波動関数で評価すれば得られることになる。

ということでGPT氏に実験コードを書いてもらおう。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import hermite

# Functions
def hermite_polynomial(n, x):
    """Hermite polynomial using scipy."""
    Hn = hermite(n)
    return Hn(x)

def harmonic_oscillator_wavefunction(n, x):
    """Harmonic oscillator eigenfunction."""
    normalization = 1 / np.sqrt(2**n * np.math.factorial(n) * np.sqrt(np.pi))
    return normalization * hermite_polynomial(n, x) * np.exp(-x**2 / 2)

def time_evolved_wavefunction(n_max, x, k, t):
    """Time-evolved wavefunction for initial exp(-ikx)."""
    wavefunction = np.zeros_like(x, dtype=np.complex128)
    for n in range(n_max):
        psi_n_x = harmonic_oscillator_wavefunction(n, x)  # Basis function in position space
        coeff = np.exp(-k**2 / 2) * (1j**n) * hermite_polynomial(n, k) / np.sqrt(2**n * np.math.factorial(n) * np.sqrt(np.pi))
        time_phase = np.exp(-1j * (n + 0.5) * t)
        wavefunction += coeff * time_phase * psi_n_x
    return wavefunction

# Parameters
n_max = 100  # number of eigenfunctions
x = np.linspace(-10, 10, 500)  # spatial points
k = 4.0  # wavevector for initial state
t_values = [0, np.pi / 2 - 0.2 ,np.pi / 2 - 0.1 ,np.pi / 2] # ここで「回転角」を調整


# Compute time evolution
wavefunctions = []
for t in t_values:
    wavefunctions.append(time_evolved_wavefunction(n_max, x, k, t))

# Plot the results (Re and Im separately)
fig, axs = plt.subplots(2, 1, figsize=(8, 12))

# Plot Re part
for i, t in enumerate(t_values):  # Plot all time values
    axs[0].plot(x, np.real(wavefunctions[i]), label=f't={t:.2f}')
axs[0].set_title("Real Part of Time-Evolved Wavefunction")
axs[0].set_xlabel("x")
axs[0].set_ylabel("Re(ψ(x, t))")
axs[0].legend(loc="upper left", bbox_to_anchor=(1.05, 1), borderaxespad=0.)

# Plot Im part
for i, t in enumerate(t_values):  # Plot all time values
    axs[1].plot(x, np.imag(wavefunctions[i]), label=f't={t:.2f}')
axs[1].set_title("Imaginary Part of Time-Evolved Wavefunction")
axs[1].set_xlabel("x")
axs[1].set_ylabel("Im(ψ(x, t))")
axs[1].legend(loc="upper left", bbox_to_anchor=(1.05, 1), borderaxespad=0.)

plt.tight_layout()
plt.show()

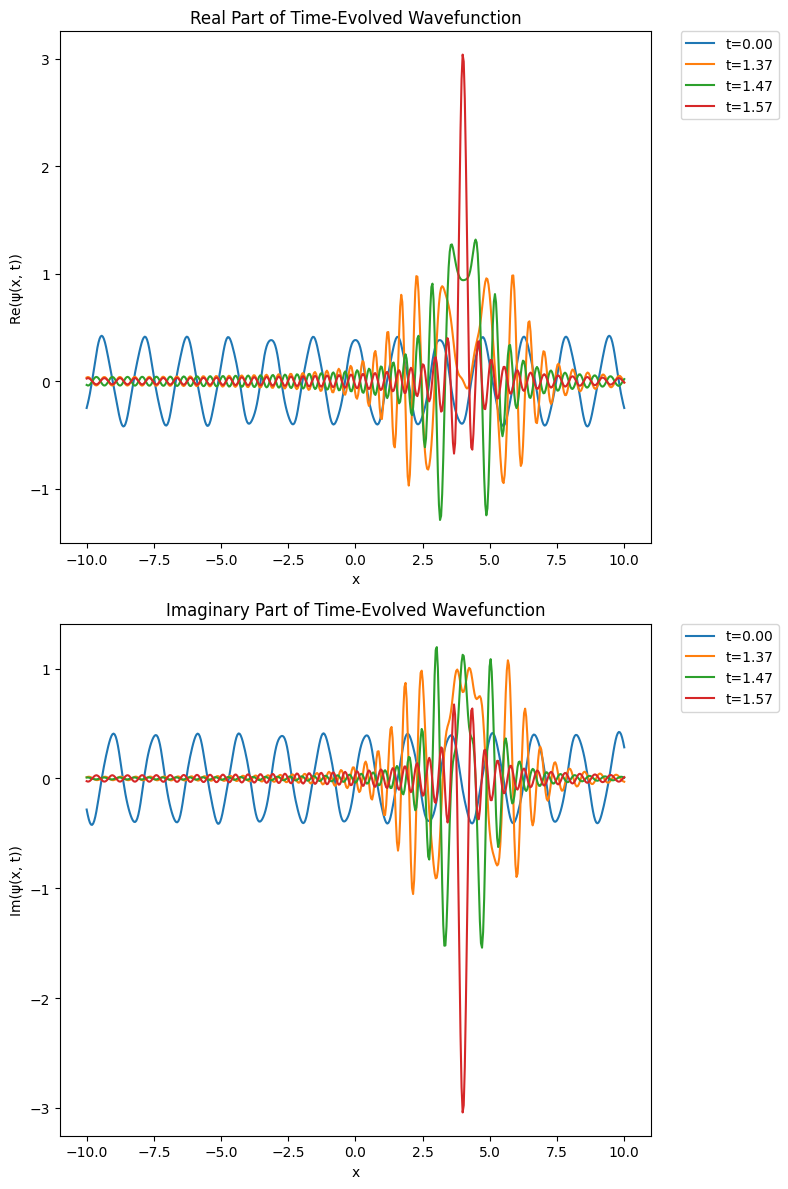
青い線が$t=0$の初期状態=入力で、つまり純粋な複素回転波だ(とはいえ打ち止めのせいか少し歪んでいる)。そこから時間発展によって$t=1.57(\pi/2)$のときには、鋭いピークになっている。つまりデルタ関数に近づいている。しかもそのピークは波数$k$の値と同じであり、要するにフーリエ変換である。デルタ関数になりきらないのは、展開に使っている$n$を$100$で打ち止めているからと考えられる。ここは大きくしすぎると内部でオーバーフローしてしまうようで、精度を上げるには別の工夫が必要になりそうだ。