でんじろう先生のこのような動画が出た。
https://www.youtube.com/watch?v=wsJn_xjiV-M&ab_channel=でんじろう先生のはぴエネ!【公式】Mr.Denjiro'sHappyEnergy!
落ちる紐がこのように落下開始地点よりも高い頂点をもつ軌道で落ちていくのは前からちょくちょく話題になっていたが、なぜこれがおきるのか簡単なモデルを見てみる。基本的にはニュートン力学の応用の範疇で考える。
この現象を再現するための最低限のセットアップ、というか最大限の理想化をしておく。それは次のようなものだ。
- 紐は密度一様で質量をもつ。
- 紐は太さを持たない。
- 紐は伸び縮みしないが、力を要せず自由に曲がる。
このため、紐の軌道は
- 慣性と重力の影響を受け、
- 紐の曲率は慣性力だけで決まり、
- 接線方向の速度は常に一定、
となる。ここで、紐の微小区間にかかる力を考える。重力と慣性力しか考えないので、紐の密度は関係がない。なので以降力の代わりに加速度で考える。
紐の微小部分にかかる力は、
の3つだ。最後の遠心力がポイントとなる。今紐の軌道しか考えていないが、直線の場合を除いて紐は非等速直線運動をしているので、紐のある部分と一緒に運動する非慣性系での力の釣り合いを考えると考慮に入れる必要がある。
紐の運動が定常であり、軌道は変化していないと仮定する。そうすると、ある関数f(x)があって、これが紐の軌道を表しており、かつ、紐のそれぞれの部分は(それぞれの部分といっしょに運動する非慣性系において)法線方向の加速度はゼロでなくてはならない。張力は常に接線方向だから遠心力と重力だけを考えればよくなる。
さて、遠心力の大きさは曲率半径できまるのだった。曲率半径とは、その点に2次で接する円の半径のことで、それがf(x)のような関数グラフなら
R(f) = \frac{(1+(f^{\prime})^2)^{\frac{3}{2}}}{f^{\prime\prime}}
となる。このときの遠心力(加速度)の大きさは、高校物理の通り\frac{v^2}{R}であり、軌道f(x)における各点の遠心力は
-\frac{v^2f^{\prime\prime}}{(1+(f^{\prime})^2)^{\frac{3}{2}}}
となる。マイナスがついているのは、曲線が曲がる側と反対側へかかる力だからだ。一方重力加速度の法線方向成分は
g(1+(f^{\prime})^2)^{-\frac{1}{2}}
というのも、傾きがf^\primeなので、これを\tan\thetaとしたときの\cos\thetaが(1+(f^{\prime})^2)^{-\frac{1}{2}}だからだ。すると釣り合い式は
-\frac{v^2f^{\prime\prime}}{(1+(f^{\prime})^2)^{\frac{3}{2}}} = g(1+(f^{\prime})^2)^{-\frac{1}{2}}
すなわち
-\frac{v^2}{g}f^{\prime\prime} = 1 + (f^\prime)^2
と単純な式になる。これは積分することができて、K=\frac{v^2}{g}、および積分定数をC,Dととると、
f(x) = K\log \cos \left(\frac{x+C}{K}\right) + D
となる。つまり、落下する自由変形有質量曲線の定常状態として\log \cosという関数形があることになる。これは両端の有限区間で-\inftyに向かう単峰形の関数だ。
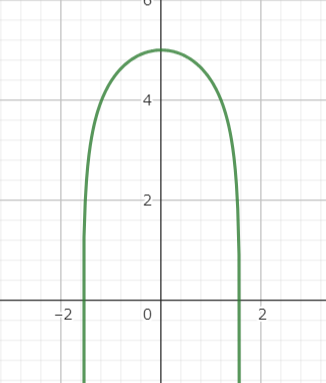
\log(\cos(x))+5の場合(https://www.geogebra.org/graphing より)
続き:

Discussion