SentenceTransformersに実装されているlossを理解する〜Triplet Loss編〜

はじめに

文章の Embedding を計算するのに一般的によく利用されている SentenceTransformers で実装されている loss がどんなものがあるのか、どういう loss なのかを、理解せず使っていなかったので、技術を利用できるようになるために雑に整理してみました。間違いに関してはコメントいただければ修正します。

Triplet Loss

Triplet Loss とは

まずは後述の内容を理解する下地を作るために TripletLoss について整理します。
Triplet Loss は Triplet Loss を使って全ての Triplet(テキスト 3 つの組み合わせ) に対して学習を行うための loss の実装になります。
アンカー$x_a$が渡されたときに、同じクラス $y_{a}$に属する正例 $x_{p}$ を埋め込んだベクトルが、別のクラスに属する負例 $y_{n}$ の埋め込んだベクトルよりもアンカーのベクトルに最低でもマージン $m$ だけ近くなることを保証するための loss になっています。
この loss の計算式としては以下の通りです。

$$L_{triplet} = \sum_{\begin{aligned} a, p, n \phantom{000} \\ y_a = y_p\neq y_n \end{aligned}} [m + D_{a, p} - D_{a, n}]_+$$

ここで、

$$D_{x, y}: \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}$$

$[\cdot]_+: max(0, ·)$の hinge 関数。triplet が満たすべき条件 ($D_{a,p} + m < D_{a,n}$) を満たしている場合、ロスがゼロになる。

m = 5 とした時の具体例で loss を計算してみると以下の通りになります。

1個目のTriplet: アンカー「魚は美味しい」、正例「寿司が好き」、負例「リンゴは赤い」
2個目のTriplet: アンカー「リンゴは赤い」、正例「一緒にリンゴを食べよう」、負例「赤い犬がいた」

1個目のTripletのloss
= m + 「魚は美味しい」と「寿司が好き」の距離(=0.2) - 「魚は美味しい」と「リンゴは赤い」の距離(=1.0)
= 5 + 0.2 - 1.0 = 4.2

2個目のTripletのloss
= m + 「リンゴは赤い」と「一緒にリンゴを食べよう」の距離(=1.2) - 「リンゴは赤い」と「赤い犬がいた」の距離(=1.3)
= 5 + 1.2 - 1.3 = 4.9

以上の合計が Triplet Loss になるので、以下の通りになります。

$$L_{triplet} = 4.2 + 4.9 = 9.1$$

Triplet Loss の課題

Alexander ら^[1]が Triplet Loss の課題として、以下が挙げられています。

• 与えた全データに対して正確に Embedding ベクトルをマッピングできるよう学習するが、その結果、大多数のわかりやすい部分のマッピングが優先され、少数のマッピングが難しい文章に関しては無視されてしまう
• 難しい Triplet をサンプリングをサンプリングする場合、データセットが大きくなるにつれて Triplet の組み合わせ数が 3 乗のオーダーで増加し、学習時間が実用上厳しくなってしまう

前者については、直感的にはたとえば同じものに対する話題かどうかの観点で類似度を出したいと言うケースであれば、「りんごは赤いです」と「魚は泳ぐのが得意です」みたいな全く違う文章を何度も何度も学習させられても学びは少ないのですが、「りんごは赤いです」と「この魚は赤いです」と言う文章は赤いと言う意味で言いたいことは一緒だが、異なる話題であれば、主語のりんごと魚の違いの概念を理解して、難しい負例を判定できるようになります。
逆に「りんごは赤いです」と「和林檎の木は茶色です」はりんごの呼び方が異なっていたり、木に対して言及しているがりんごのことに言及しているので同じ話題と認識することで、呼び方の違いや状態の違いの概念を理解できることで難しい正例を判定できるようになります。
「じゃあ上記の難しい正例・負例だけ学習すれば良いのか？」というと実はそうではありません。仮に最も難しいサンプルばかりを利用して学習させてしまうと、データ内の異常値が頻繁に選ばれることになってしまうので、通常のマッピングを学習できなくなってしまいます。
なので、適度な負例^[2]や正例^[3]をサンプリングことが一般的に行われています。
ただ、これらの方法は最新の大量のデータを埋め込んだ上でそれらのデータ間のすべての距離行列を計算してそれを元にサンプリングする必要があるため、かなり計算時間がかかってしまう欠点があります。

後者については、上記から難しい Triplet を程よくサンプリングしないといけないのですが、その場合、Embedding ベクトルを学習するための関数の結果を全サンプルに対して全パターンの組み合わせに対して推論してその結果をもとに良い感じにサンプリングする必要があるので、計算コストが膨大になってしまうためです。

BatchHardTripletLoss

BatchHardTripletLoss とは

上記に書いた Triplet Loss の課題を解決した Alexander ら^[1:1]が提案している loss 関数になります。

Triplet Loss との違いは、クラスをランダムにサンプリングして P 個のクラス（トピックとかタグとか）を取り出し、各クラスの中から K 個 ランダムにサンプリングしてバッチを作る点です。
つまり、以下の図のようになります。

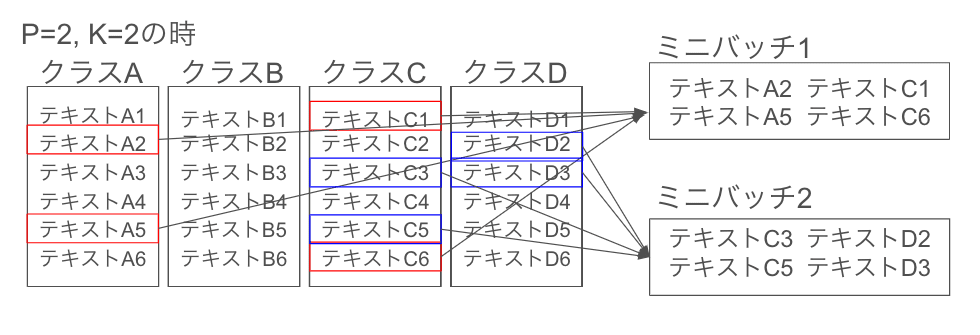
Triplet loss では、訓練データ全体から以下のような手順で、難しい Triplet をサンプリングすることが一般的です。

1. 毎回学習データ全体に対して、埋め込みベクトルを計算します
2. 得られた埋め込みベクトルの全てのサンプルのペア間の距離を計算します。
3. 難しい正例を選ぶために、各アンカーに対して、同じクラスに属するサンプルの中で最も距離が大きいものを選択します。
4. 難しい負例を選ぶために、各アンカーに対して、異なるクラスに属するサンプルの中で最も距離が小さいものを選択します。

図で表すと以下のようになります。

これはデータセットが大規模になると、計算コストがかなり高くなります。

そこで、BatchHardTripletLoss では、バッチ内に含まれるサンプルだけを考慮して難しい Triplet を選択します。つまり、バッチ内で最も難しい正例と最も難しい負例を選んで Triplet loss を計算するわけです。
バッチ内のサンプルは、データ全体から見れば一部の小さなサブセットであり、そのサブセット内で選ばれた難しい Triplet は、データ全体で見れば「そこそこ難しい Triplet」、すなわち「moderate triplets」ということができます。
この「moderate triplets」がなぜ良いのかというと、あまりに難しい Triplet ばかりを使うと、外れ値の影響を受けすぎてかえって学習が不安定になってしまうからです。その一方で、簡単すぎる Triplet では学習が進みません。
その中間、つまり「ほどよく難しい Triplet」を選択するのが Batch Hard の狙いであり、バッチ内の難しい Triplet は、データ全体で見れば「穏やかな Triplet」に相当することになります。
これにより、Triplet 選択の計算コストを抑えつつ、学習に効果的な Triplet を選択できるようになるわけです。

数式としては以下です。

$$L_{BH}(\theta; X) = \overbrace{\sum_{i=1}^{P} \sum_{a=1}^{K}}^{\text{all anchors}} [ m + \overbrace{\underset{p=1,...,K}{max} D (f_{\theta} (x_{a}^{i}), f_{\theta} (x_{p}^{i}))}^{\text{hardest positive}} - \overbrace{\underset{\tiny{\begin{aligned}j=1...P \\ n=1...K \\ j \neq i \end{aligned}}}{min} D(f_{\theta} (x_{a}^{i}), f_{\theta} (x_{n}^{j}))}^{\text{hardest negative}}]_+$$

ここで、

$$D(x, y): \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R} \\ f_{\theta} (x): \mathbb{R}^F \to \mathbb{R}^D \\ x_{a}^{i}: i はミニバッチ内のクラスのインデックス、そのクラスのテキストを指すアンカーのインデックスなので、x_{a}^{i}自体はアンカーのテキストを示す。$$

数式が複雑になったように見えますが、数式の loss を計算するための Triplet を作るときに、max の部分ではバッチ内の各サンプル a について距離が最大になる正例を使うことを明示しています。
これによりバッチ内で最も似ていないと言われている正例（つまり、モデルにとって距離を正しく出すのが難しい正例）を loss の計算に使うことができます。
負例の場合には同様に min を取ることで最小の距離になる負例を利用して、バッチ内で最も似ているようにモデルから見えている難しい負例を loss の計算で利用することになります。このことから Batch Hard と呼ばれます。
こうすることで全サンプルの中から難しい異常値だけを抽出するわけではなく、あくまで"バッチの中"から難しいものを抽出することになるので、程々に難しい正例、負例がサンプリングされるので、Triplet loss の課題を解決したものになります。

SentenceTransformers の公式ドキュメントでは、Hard triplets の定義は以下のように表記されているのですが、margin の記述がないので、論文の定義とは異なるのが気になりました。公式のドキュメントの References のソースコードを見ても margin は利用されているので、何故…という気持ちになりました。

Triplets where the negative is closer to the anchor than the positive, i.e., distance(anchor, negative) < distance(anchor, positive).

BatchAllTripletLoss

「別に max とか min に絞って loss を計算しなくてもサンプリングしたバッチの全部の Triplet の組み合わせを使って学習しても良いのでは？」という疑問もあるかと思います。そのアプローチについてはこの論文では Batch All と呼んでいます。
バッチサイズが PK （P 個のクラスから各 K 個のサンプルで作ったバッチ）の場合を考えます。
この時の手順としてバッチの中で Triplet の組み合わせを作る手順は以下の通りです。

1. あるアンカーサンプルを固定します。
2. バッチ内の同じクラスの他の全てのサンプルを正例とします。
3. バッチ内の別のクラスの全てのサンプルを負例とします。
4. 上記の 2 と 3 の組み合わせで作れる全ての Triplet を作ります。
5. これを全てのアンカーサンプルに対して行います。

アンカーサンプルの数は PK、各アンカーに対して正例の候補は(K-1)、負例の候補は P(K-1)となるので、全 Triplet の数は PK(PK-K)(K-1)となります。

例えば P=4, K=4 の場合、64 個の Triplet を作成することになります。

このアプローチは BatchHardTripletLoss と比べて、より多くの Triplet を使って学習できるメリットがある一方で、計算量が増えるというデメリットがあります。

BatchAllTripletLoss を数式は以下の通りです。

$$\mathcal{L}_\text{BA}(\theta; X) = \overbrace{\sum_{i=1}^P \sum_{a=1}^K}^{\text{all anchors}} \quad \overbrace{\sum_{\tiny{\begin{aligned}p=1\\ p \neq a\end{aligned}}}^K}^{\text{all positives}} \quad \overbrace{\sum_{\tiny{\begin{aligned}j=1 \\ j\neq i\end{aligned}}}^P \sum_{n=1}^K}^{\text{all negatives}} \left[ m + d^{i,a,p}_{j,a,n} \right]_+$$

ここで、

$$d^{i,a,p}_{j,a,n} = D \left(f_\theta(x^i_a), f_\theta(x^i_p)\right) - D \left(f_\theta(x^i_a), f_\theta(x^j_n)\right)$$

ただ、この BatchAllTripletLoss では学習が進んでいくと、作成したバッチの多くの$m + d^{i,a,p}_{j,a,n}$の値が 0 になってしまいます。
これにより何が起こるかというと、BatchAllTripletLoss は$m + d^{i,a,p}_{j,a,n}$のバッチ内の全てのペアに対する合計なので、大部分が 0 になってしまって学習効率が下がってしまうことになります。

例えば、以下のような P=2, K=2 のバッチ があったとします。

• アンカー「りんごは赤いです」、正例「りんごを持っています」、負例「この魚は赤いです」
  • $m + d^{i,a,p}_{j,a,n}$=0
• アンカー「りんごは赤いです」、正例「りんごを持っています」、負例「赤い魚がいた」
  • $m + d^{i,a,p}_{j,a,n}$=0
• アンカー「りんごを持っています」、正例「りんごは赤いです」、負例「この魚は赤いです」
  • $m + d^{i,a,p}_{j,a,n}$=0
• アンカー「りんごを持っています」、正例「りんごは赤いです」、負例「赤い魚がいた」
  • $m + d^{i,a,p}_{j,a,n}$=0
• アンカー「この魚は赤いです」、正例「赤い魚がいた」、負例「りんごは赤いです」
  • $m + d^{i,a,p}_{j,a,n}$=0
• アンカー「この魚は赤いです」、正例「赤い魚がいた」、負例「りんごを持っています」
  • $m + d^{i,a,p}_{j,a,n}$=0.9
• アンカー「赤い魚がいた」、正例「この魚は赤いです」、負例「りんごは赤いです」
  • $m + d^{i,a,p}_{j,a,n}$=0
• アンカー「赤い魚がいた」、正例「この魚は赤いです」、負例「りんごを持っています」
  • $m + d^{i,a,p}_{j,a,n}$=0

この時、BatchAllTripletLoss の学習時のミニバッチ全体の loss は 0.9 となります。
これを triplet の総数で割ることで 平均の Triplet loss を求めることになるのですが、計算すると 0.9/8=0.1125 となり、平均の Triplet loss の値がかなり小さくなってしまいます。
今回の例では 8 件ですが、100000 件のうち、0.9 が一個となると loss は 0.000009 となってしまいます。
これにより、有効なサンプルの loss が洗い流されてしまうことでうまく学習できなくなります。
Alexander ら^[1:2]は論文中の実験でこの仮説を検証するために、0 にならなかった loss の項のみで平均化する実験も行い、実際に精度が向上したことを確認しています。

BatchHardSoftMarginTripletLoss

BatchHardSoftMarginTripletLoss は BatchHardTripletLoss における hinge 関数（$[\cdot]_+$）を
Softplus 関数($ln(1 + exp(\cdot))$)に変更したものになります。

BatchHardSoftMarginTripletLoss を数式にすると以下の通りです。

$$L_{BHSoft}(\theta; X) = \overbrace{\sum_{i=1}^{P} \sum_{a=1}^{K}}^{\text{all anchors}} ln(1 + exp(\overbrace{\underset{p=1,...,K}{max} D (f_{\theta} (x_{a}^{i}), f_{\theta} (x_{p}^{i}))}^{\text{hardest positive}} - \overbrace{\underset{\tiny{\begin{aligned}j=1...P \\ n=1...K \\ j \neq i \end{aligned}}}{min} D(f_{\theta} (x_{a}^{i}), f_{\theta} (x_{n}^{j}))}^{\text{hardest negative}}))$$

hinge 関数だと triplet が満たすべき条件である$m + D_{a, p} < D_{a, n}$を満たしていると、loss が 0 になってしまって、前述のような状況になってしまいます。
Softplus 関数は入力が大きい正の値の場合は入力とほぼ等しい値を出力し、入力が大きい負の値の場合は"ほぼ" 0 を出力します。この"ほぼ"0 というのがポイントで、$D_{a, p} - D_{a, n}$が負の値になってもさらにアンカーと正例の距離を縮める方向か、アンカーと負例の距離を広げる方向に学習が進められる特徴があります。
論文では画像による人物同定のタスクを解いているので、同一人物のサンプルをできるだけ近づけることが望ましいという考えに基づいて採用されています。

ここまでのそれぞれの Loss による性能

「In Defense of the Triplet Loss for Person Re-Identification」での比較結果は以下の通りです。

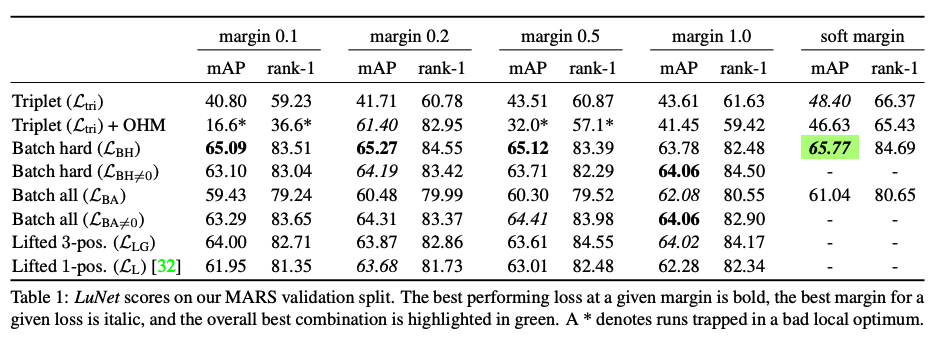
人物再同定のタスクにおいては BatchHardSoftMarginTripletLoss が一番良い精度出たことが見受けられます。Sentence Embedding のタスクにおいても、同じクラスのサンプルをできるだけ近づけることが望ましいと言えると思うので、同じように一番 BatchHardSoftMarginTripletLoss がうまく機能するのかは実験してみたくなりました。

BatchSemiHardTripletLoss

BatchSemiHardTripletLoss は Florian Schroff ら^[3:1] が提案した BatchHardTripletLoss の難しい Triplet の条件を Semi-hard と呼ぶ緩めな条件を使っている loss になります。
BatchHardTripletLoss では、各アンカーに対して、モデルから見て最も難しい正例（アンカーとの距離が最大の正例）と最も難しい負例（アンカーとの距離が最小の負例）を選択していました。
BatchSemiHardTripletLoss では、正例は全パターン利用するのですが、負例についてはアンカーからの距離が正例よりも遠い負例だけに絞って選択しています。すなわち $D_{a, p} < D_{a, n}$ を満たすことになります。このような負例を Semi-Hard と呼びます。

これを他の loss と同様な形で数式で表現すると以下になります。(数式が見当たらなかったので私の方で考えたので、間違ってたらごめんなさい。)

$$L_{BSH} = \overbrace{\sum_{i=1}^P \sum_{a=1}^K}^{\text{all anchors}} \quad \overbrace{\sum_{\tiny{\begin{aligned}p=1 \\ p \neq a\end{aligned}}}^K}^{\text{all positives}} \quad \overbrace{\sum_{\tiny{\begin{aligned}j=1 \\ j \neq i\end{aligned}}}^P \sum_{\tiny{\begin{aligned}n=1 \phantom{OOOOOOOOOO} \\ D (f_{\theta} (x_{a}^{i}), f_{\theta} (x_{p}^{i}))< D(f_{\theta} (x_{a}^{i}), f_{\theta} (x_{n}^{j})) \end{aligned}}}^K}^{\text{semi hard negatives}} [D (f_{\theta} (x_{a}^{i}), f_{\theta} (x_{p}^{i})) - D(f_{\theta} (x_{a}^{i}), f_{\theta} (x_{n}^{j})) + m]_+$$

BatchSemiHardTripletLoss では全てのアンカーと正例のペアを利用しますが、その理由について、Florian Schroff ら^[3:2]はミニバッチ内のハードなアンカー-正例ペアと全てのアンカーと正例のペアの直接比較は行っていないものの、全てのアンカーと正例のペアのアプローチの方が学習が安定しており、学習の初期段階でわずかに速く収束すると説明しています。

また、学習の初期段階で最も難しい負例を選択すると、悪い局所最適解に陥る可能性があると指摘しており、これを緩和するために、先述の$D_{a, p} < D_{a, n}$ の条件が$x_n^j$ を選択しています。

終わりに

今回は SentenceTransformers の以下の loss について整理しました。

• BatchAllTripletLoss
• BatchHardTripletLoss
• BatchSemiHardTripletLoss
• BatchHardSoftMarginTripletLoss

AnglELoss と ContrastiveTensionLoss と CoSENTLoss と MatryoshkaLoss が何となく気になっているので、次はその辺を調べてみようかと思います。

脚注

1. Alexander Hermans, Lucas Beyer, Bastian Leibe. In Defense of the Triplet Loss for Person Re-Identification. https://arxiv.org/pdf/1703.07737.pdf

2. Florian Schroff, Dmitry Kalenichenko, James Philbin. FaceNet: A Unified Embedding for Face Recognition and Clustering. https://arxiv.org/pdf/1503.03832.pdf

3. Hailin Shi, Yang Yang, Xiangyu Zhu1, Shengcai Liao1, Zhen Lei1,Weishi Zheng, Stan Z. Li. Embedding Deep Metric for Person Re-identification: A Study Against Large Variations. https://arxiv.org/pdf/1611.00137.pdf