複数多項式二次篩法 (MPQS) (理論)

そろそろ次のアルゴリズム、複数多項式二次篩法 (MPQS) に移行します。

概要

QSでは

$$x2≡x2−N(modN) x^2 \equiv x^2-N \pmod{N}$$

として $x2−Nx^2-N$ を篩っていましたが、MPQSでは適当な 3 数 $aa$, $bb$, $cc$ を設定して

$$(ax+b)2≡(ax+b)2−N(modN)=a(ax2+2bx+c) \begin{aligned} (ax+b)^2 &\equiv (ax+b)^2-N \pmod{N}\\ &= a(ax^2+2bx+c) \end{aligned}$$

を篩っていきます。$aa$, $bb$, $cc$ に関する制約は追々設定していきますが、今はこの式変形が成り立つものとして進めてください＆名前の「複数」は一旦忘れてください。
このとき、実質的に QS での $x2−Nx^2-N$ と MPQS での $(ax+b)2−N(ax+b)^2-N$ が同じ程度の数になることが期待されますが MPQS では $aa$ を因数に持つことが確定するように係数設定をするので、本質的に篩をかける数 $ax2+2bx+cax^2+2bx+c$ はその分小さく、つまり smooth になりやすくなります。

参考までに QS と MPQSで同じ幅 $2M2M$ の篩をかけたとするときの数の大きさを比較してみましょう。
QS では $(N−M,N+M)(\sqrt{N}-M,\sqrt{N}+M)$ で $f(x)=x2−Nf(x)=x^2-N$ を篩うので、

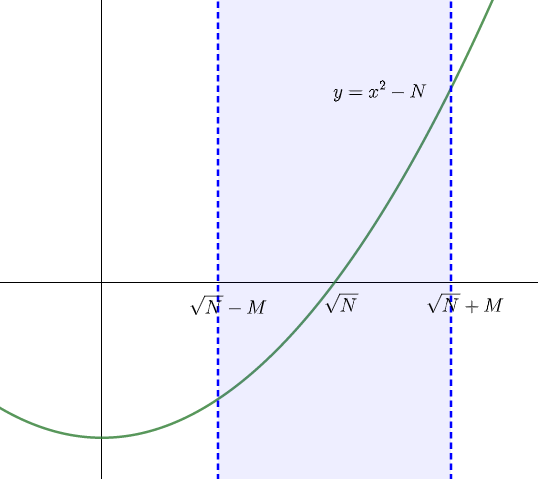
QSで篩う範囲

$$max⁡f(x)=f(N+M)=2NM+M2≃2NM \max f(x) = f(\sqrt{N}+M) = 2\sqrt{N}M + M^2 \simeq 2\sqrt{N}M$$

一方で MPQS では $(−M,M)(-M,M)$ で $f(x)=(ax+b)2−N=ag(x)f(x)=(ax+b)^2-N=ag(x)$ を篩うので

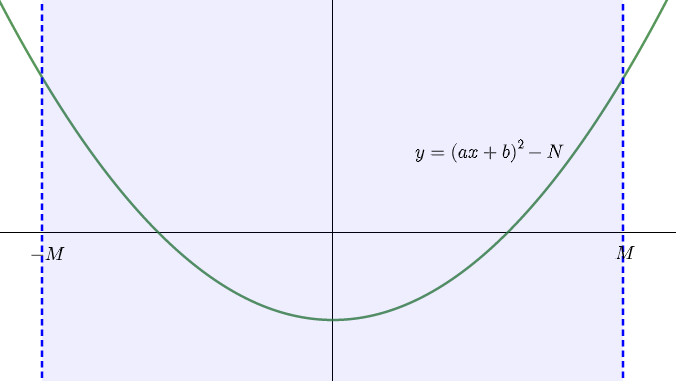
MPQSで篩う範囲

smoothness のことだけを考える場合は $g(x)=ax2+2bx+cg(x)=ax^2+2bx+c$ を考えて

$$max⁡∣g(x)∣=max⁡(g(M),−g(0))=1amax⁡((aM+b)2−N,N−b2) \max |g(x)| = \max(g(M), -g(0)) = \dfrac{1}{a}\max((aM+b)^2-N, N-b^2)$$

となります。こちらは候補の両方の値が同じくらいの時に全体として最小になることが期待されるので $b≪aMb \ll aM$ として

$$(aM)2−N≃N∴a≃2NM (aM)^2-N \simeq N\\ \therefore a \simeq \dfrac{\sqrt{2N}}{M}$$

のときに

$$max⁡∣g(x)∣≃N/a=NM2 \max |g(x)| \simeq N/a = \frac{\sqrt{N}M}{\sqrt{2}}$$

の smoothness が対象となります。これは QS と比較してざっくり $1/22≃1/2.81/2\sqrt{2} \simeq 1/2.8$ となっています。

さらに MPQS では異なる $(a,b)(a,b)$ を設定することで実質的に異なる値を篩うことになるので $MM$ をより小さく設定することができ、$g(x)g(x)$ の絶対値をより小さく、より smooth になりやすくすることができます。(「複数」という名前を思い出したかのように)

制約

では上記のような計算ができる $aa$, $bb$, $cc$ の制約について見直していきましょう。
まず $aa$ については

$a(ax2+2bx+c)a(ax^2+2bx+c)$ を篩っていきます。

から、

$$a=(平方数)×(smoothな数)(A1) a = ({\rm 平方数}) \times ({\rm smooth な数}) \tag{A1}$$

となる必要があります。そうでなければ $a(ax2+2bx+c)a(ax^2+2bx+c)$ が smooth にならない(対偶)ので。ここで平方数の部分は FB に含まれない素数を使っていても構いませんが、どの $aa$ を使ったものか保持しておく必要はあります。あと後ろの説明から $aa$ の素因数 $pip_i$ は $(N/pi)=1(N/p_i)=1$ (平方剰余) を満たす必要があります。

次に $bb$ の制約について最初の式を変形させてみましょう。

$$(ax+b)2−N=a(ax2+2bx+c)a2x2+2abx+b2−N=a2x2+2abx+acb2−ac=N (ax+b)^2-N = a(ax^2+2bx+c)\\ a^2x^2+2abx+b^2-N = a^2x^2+2abx+ac\\ b^2-ac = N$$

するとこの式から

$$b2≡N(moda)(B1) b^2 \equiv N \pmod{a} \tag{B1}$$

という条件が導かれます。この合同方程式は $aa$ の素因数分解を利用して解きます。具体的には各素因数 $pip_i$ について $bi2≡N(modpi)b_i^2 \equiv N \pmod{p_i}$ をこちらで解いて中国剰余定理で復元させます。^[1] 読んでる参考書類には尽く $b<a/2b < a/2$ と書いてますが、どこからその条件が出てくるか分かりません。

$cc$ については同じ式から

$$c=b2−Na c = \frac{b^2-N}{a}$$

で求まりますが使うことがないので計算しません。

MPQS と SIQS

MPQS は篩に使う式の数を増やすことで篩う範囲を絞り、効率的に smooth な関係式を得るアルゴリズムです。この複数の式を作る方法にも少しバリエーションというか発展があるので、そちらも紹介します。

オリジナルの MPQS では $aa$ の条件として平方数であることを採用していたので、$bb$ を求める計算の簡単さから FB に含まれない ($P0P_0$ より少し大きな) 素数 $pip_i$ を使って

$$a=pi2(Npi)=1 a = p_i^2\\ \left(\frac{N}{p_i}\right) = 1$$

という条件で $aa$ の数を増やし、式の数を稼ぎます。

一方、この方式ではあまり式の数を増やすと $bb$ の計算や篩に使う $xx$ の初期値計算(式あたり FB のサイズだけ必要) が必要になるので、これらの計算コストが高い事がネックになります。それに対する対策が 自己初期化二次篩法 (SIQS; Self-Initializing QS) です。

SIQS では $aa$ を FB のいくつか($kk$ 個とする)の素数の積として固定します。

$$a=∏pi∈FBpi a = \prod_{p_i\in {\rm FB}}p_i$$

一方で $bb$ については式 (B1) から $b2≡N(modpi)b^2\equiv N \pmod{p_i}$ という関係が成り立つので、各 $pip_i$ に対して $b=±bib=\pm b_i$ の 2 つの解が得られ、中国剰余定理で復旧した $bb$ には $∣b∣<a|b|<a$ を考慮しても $2k−12^{k-1}$ 個のバリエーションを作れることになります。

このとき、$aa$ の計算に使っていた素数については $a(ax2+2bx+c)a(ax^2+2bx+c)$ の変形を考えて 1 ずつの指数が確定します。指数が 2 以上になるケースについては smooth だという判断をした後で具体的に求めることになります。

逆に $aa$ の計算に使っていない $pi∈FBp_i\in {\rm FB}$ について $xx$ の初期値を計算するときには $ri2≡N(modpi)r_i^2\equiv N\pmod{p_i}$ として

$$x≡(−b±ri)a−1(modpi) x \equiv (-b\pm r_i)a^{-1} \pmod{p_i}$$

となります。ここで式によって変わるのは $bb$ だけなので $rir_i$ や $a−1a^{-1}$ を保存しておくと計算が素早くなりますし、さらに $2ria−12r_ia^{-1}$ も保存しておけば一方の解 $x0≡(−b−ri)a−1x_0\equiv (-b-r_i)a^{-1}$ からもう一方 $x1≡(−b+ri)a−1=x0+2ria−1x_1\equiv (-b+r_i)a^{-1}=x_0+2r_ia^{-1}$ を少ない計算量で求めることができます。

脚注

1. TODO:中国剰余定理で記事を書く