グラフニューラルネットワークって何?③GNNと畳み込み
CNNはGNNの特殊例?
こんにちは。前回から随分と期間が空いてしまった。TransformerとGNNの関係について述べた前の記事を書き終えたのち、一旦燃え尽きてしまったのと、色々忙しかったため、この記事の更新が止まっていたが、ちょうど時間ができたので最後の章を書こうと思う。やはり理論ばかりでは読んでいて面白くないかもとも考えたので、最後に簡単なチュートリアルのようなものを公式のページ等を参考に作成してみた。
まずは、前回の宣言通り、CNNとGNNの関連性について軽く説明したい。AIや深層学習を勉強していると、よく目にするものに、CNN (Convolutional Neural Network)というモデルが存在する。深層学習の始まりとも言えるAlexNetも確かCNNだった気がする。実はこのCNNは、GNNの"特殊な形"として理解することができる。この記事で「CNNはGNNの特殊例である」ことをやさしく解説することができれば幸いである。
CNNとGNNの違い
| CNN | GNN | |
|---|---|---|
| 入力データ | 格子上のデータ (画像など) | 任意のグラフ構造 |
| ノード | ピクセル | グラフのノード |
| エッジ | 固定(上下左右の隣接など) | 自由に設計可 |
| 情報伝播 | カーネルで近郊情報を集める | 隣接ノードの情報を集める |
ここで視点を変えると、画像は、ピクセルが格子状に並んだデータであると捉えることができる。
- 各ピクセル = ノード
- 隣接したピクセル = エッジ
として考えれば、画像は格子グラフ (grid graph)として表すことが可能となる。
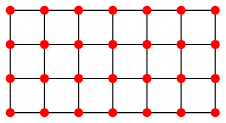
WolfmanMathWorldより格子グラフ
CNN = GNN on Grid Graph
GNNの基本の形式(message passing)は以下のような形だが
これは「隣接ノードから情報を集めて自分の状態を更新する」ことを意味している。
CNNも実際は同じことをしている。
| 記号 | 説明 |
|---|---|
| k層目の特徴マップの(i, j)位置の出力値(この位置の特徴量) | |
| 活性化関数(ReLUやSigmoidなど) | |
| カーネル内の位置インデックス(例えば3×3なら-1〜1など) | |
| (i, j)周辺のピクセル位置の集合(カーネルで見る範囲) | |
| カーネルの重み(各周辺ピクセルに掛ける重み、学習パラメータ) | |
| 前の層の入力(特徴マップ)の(i+m, j+n)位置の値 | |
| バイアス項(重みに加えて足される定数) |
つまり、CNN = 格子グラフ上でのGNNと考えることができる。
Graph Convolutional Network
せっかく畳み込みの話に触れたので、GCNについても軽く触れておこう。GNNの中でも代表的なモデルのひとつに GCN(Graph Convolutional Network)が存在する。GCNは、グラフ構造を持つデータに対して、CNNのような「畳み込み」を定義することを目的とした手法である。この記事では紹介程度にとどめるが、GCNはGNNを扱う上で最も基本的なモデルの一つである。
数式(簡略版)
| 記号 | 説明 |
|---|---|
| l層目のノード特徴行列 | |
| 正規化された隣接行列(自己ループ込み) | |
| 学習可能な重み行列 | |
| 非線形関数(例:ReLU) |
要は各ノードを表す特徴ベクトル(H内のベクトル)から隣接行列を使うことで、対象のノードに隣接しているノード群のみを抽出し、Wで重みづけして、非線形関数に入力していると考えることができる。
PyTorch Geometric
さて、座学的な知識の話はここまでにして、実際にグラフニューラルネットワークを扱うためのフレームワークであるPyTorch Geometricを使って簡単なサンプルコードを書いてみよう。ここでは、Cora論文引用ネットワークをグラフに見立てて、各ノードである論文のカテゴリ分類を行う「ノード分類」を行うものとする。
概要
このコードでは、PyTorch Geometricに組み込まれている「Cora」データセットを使用し、グラフ構造を持つ論文ネットワークに対してノード分類を行う。ノードは論文、エッジは引用関係、ノードの特徴はBag-of-Wordsで表現された単語情報、ラベルは論文の研究分野カテゴリ(全7種)。GCNモデルを用いて、各論文がどの分野に属するかを分類することを目的とする。学習にはノードの一部(train_mask)のみを使い、残りはバリデーション・テストに使用する。
コード
準備:
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid
PyTorchも必要になるので注意。
データセットの読み込み:
dataset = Planetoid(root='./data', name='Cora')
data = dataset[0]
ちなみに今回はデータセットをそのまま読み込んでいるので特に意識はしていないが、PyTorch Geometricではグラフを隣接行列として扱っている。隣接行列が何かということは、ここでは説明を省くので、気になった人はリンクから飛んで確かめて欲しいが、各ノード同士のつながりを行列の形で表現したものであると考えてしまって構わない。グラフを行列として扱うことで巨大なグラフデータのバッチ化といったことまで可能になるのだが、詳しくは公式の説明に譲ることとする。
モデルの定義:
class GCN(torch.nn.Module):
def __init__(self):
super().__init__()
self.conv1 = GCNConv(dataset.num_node_features, 16)
self.conv2 = GCNConv(16, dataset.num_classes)
def forward(self, data):
x, edge_index = data.x, data.edge_index
x = self.conv1(x, edge_index)
x = F.relu(x)
x = self.conv2(x, edge_index)
return x
構造としては二層のGCNを重ねたものとなっている。この辺はPyTorchと書き方が似通っているので、PyTorchを使ったことがいる人がいたら馴染み深いかもしれない。
学習:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = GCN().to(device)
data = data.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
model.train()
for epoch in range(200):
optimizer.zero_grad()
out = model(data)
loss = F.cross_entropy(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
こちらもPyTorchと同じような書き方。Optimizerには定番のAdamを使う。
評価結果
model.eval()
pred = model(data).argmax(dim=1)
correct = (pred[data.test_mask] == data.y[data.test_mask]).sum()
acc = int(correct) / int(data.test_mask.sum())
print(f'Test Accuracy: {acc:.4f}')
精度は約80%であった。簡易的なモデルの構造にしてはよくできた方だと感じる。
まとめ
さて、この記事では、GNNと畳み込みの関連性について述べ、後半では実際にコードを通じて、GNNで解けるタスクの一つであるノード分類をGCNを使ってやってみた。ここまでの記事シリーズがほとんど座学的な内容(特に二つ目の記事はいささか退屈に感じた人もいたかもしれない)であり、知識に重きを置いてきたのだが、最後のこの記事ではしっかり実践につながるような内容でコードサンプルを提供できたことは実に嬉しい。
ここまででグラフとGNNに関するこの一連のシリーズ記事は幕引きとなる。私も途中でモチベーションがなくなったり、時間がなくなったりして色々あったが、いったん幕を引けて嬉しい。ここまで書いてきて感じたが、シリーズにするよりも単発記事の方が圧倒的に書きやすいし、モチベーションや時間の心配がなかったので次からはそうしようと思った。暑さが続き、夏バテに苦しむ季節がまだまだ続きそうである。これを読んでいる皆様におかれましては是非とも健康に気をつけて無理せず生きてもらいたい。私も無理せず、気が向いた時にでも次の記事を書くかもしれない。
Discussion