😊
Analysis
書きかけ
Cauchy’s Convergence Test
The number sequence a_n ∈ K (n ∈ N) is convergent if and only if it is a Cauchy sequence.
Cauchy sequenceはa_nをKの要素を持つ数列として、以下を満たすもの。
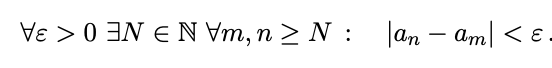
Cauchy Criterion
- https://en.wikipedia.org/wiki/Cauchy's_convergence_test
- infinite numerical sumが収束するときの必要十分条件は、Sequence of partial sumsが収束する
hyperharmonic series or a p-series
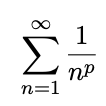
Alternating Series
Leibniz type
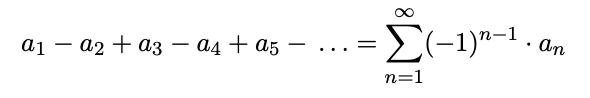
Root test
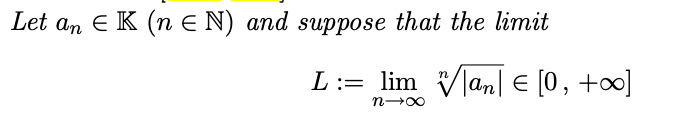
- L < 1ならば、absolutely convergent
- L > 1ならば、divergent
適用する場面は、数列にn乗があるとき等。
Ratio test
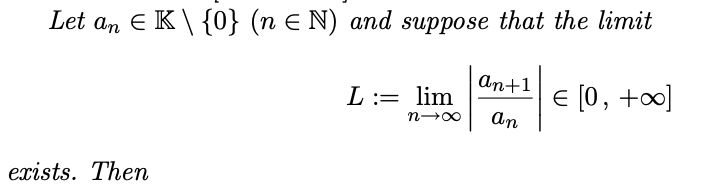
- L < 1ならば、absolutely convergent
- L > 1ならば、divergent
適用する場面は、数列に階乗があるとき等。
- L < 1ならば、absolutely convergent
- L > 1ならば、divergent
Discussion