2NF, 3NFの定式化と3NFの定義における2NFの冗長性

データベースにおける関数従属性や正規形（例えば2NFや3NFなど）の解説資料は、数学的に曖昧なことが多い。
そこで本記事ではできるだけ曖昧さを減らすために、集合論の言葉を用いて関数従属性や2NF、3NFなどの概念を定式化する。

また、その定式化を用いて、よくある3NFの定義に冗長性があることを示す。
3NFの定義の冗長性について、ここで少しだけ説明する。
あるリレーションスキーマが3NFであるとは、次の(1)と(2)を満たすことと定義されることが多い。

(1) 2NFである（任意の非キー属性が任意のキー候補に完全関数従属する）
(2) 任意の非キー属性が任意の候補キーに非推移的に関数従属する

実は(1)は冗長である。本記事では、2NFと3NFなどの概念を定式化し、(1)が冗長であること、すなわち「(2)ならば(1)」であることを示す。

tl;dr

「(2)ならば(1)」であることについて。
「(2)ならば(1)」を示すために、その対偶「(1)でないならば(2)でない」を示す。
ここでは例を用いて「(1)でないならば(2)でない」こと、すなわち「2NFではないならば、ある非キー属性がある候補キーに推移的に関数従属する」ことをざっくりと説明する。

学生の所属する部活動に関するリレーションスキーマを考える。属性は学籍番号・学生氏名・部活動の3つとする。

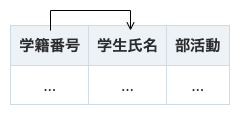
このリレーションスキーマには、「{学籍番号}→{学生氏名}」いう関数従属性がある。
同姓同名の可能性を考え、「{学生氏名}→{学籍番号}」という関数従属性はないとする。
また兼部の可能性を考え、「{学籍番号}→{部活動}」という関数従属性もないとする。

このリレーションスキーマは2NFではない。
なぜなら、関数従属性「{学籍番号, 部活動}→{学生氏名}」は部分関数従属だからである。
（{学籍番号, 部活動}はキー候補、学生氏名は非キー属性で、「{学籍番号}→{学生氏名}」という関数従属があることに注意）

「2NFでない」ことから「ある非キー属性がある候補キーに推移的に関数従属する」も言える。
この例でいうと、部分関数従属性「{学籍番号, 部活動}→{学生氏名}」は
「{学籍番号, 部活動}→{学籍番号}→{学生氏名}」
という推移的な関数従属と見れるからである。
一般に、候補キー→{非キー属性}という関数従属性は部分関数従属であれば推移的関数従属である。

この記事では、まずリレーションスキーマや関数従属性、2NF、3NFなどの概念を集合論の言葉を用いて定式化する。
そして「2NFではないならば、ある非キー属性がある候補キーに推移的に関数従属」こと、すなわち「3NFの定義の2NFであるという条件は冗長である」ことを証明する。

準備: 集合論

部分集合

集合 $A$ が集合 $B$ の部分集合であることを $A \subseteq B$ と書き、集合 $A$ が集合 $B$ の真部分集合であることを $A \subsetneq B$ と書くことにする。

べき集合

集合 $X$ に対して、$X$ の部分集合全体の集合を $X$ のべき集合といい、$\mathcal{P}(X)$ と表す。

$X$ のべき集合は $2^X$ と書くこともあるが、本記事では $X$ の部分が複雑な場合があるので $\mathcal{P}(X)$ と書くことにする。

写像の制限

$X, Y$ を集合とする。写像 $f\colon X\to Y$ と部分集合 $A \subseteq X$ に対して、写像 $f|_A\colon A \to Y,\ f|_A(x) = f(x)$ を写像 $f$ の $A$ への制限という。

直積

$X$ を集合とし、$(D(x))_{x\in X}$ を集合族とする。集合族 $(D(x))_{x\in X}$ の直積 $\prod_{x\in X} D(x)$ を次のように定義する。

$$\prod_{x\in X} D(x) = \left\{t\colon X \to \bigcup_{x\in X} D(x) \mid \text{任意の $x\in X$ に対して $t(x) \in D(x)$}\right\}$$

極小元

$X$ を集合とし、$\mathcal{K} \subseteq \mathcal{P}(X)$ とする。このとき、$A \subseteq X$ が $\mathcal{K}$ の（包含関係における）極小元であるとは、$A \in \mathcal{K}$ であって、$\mathcal{K}$ の元に $A$ の真部分集合が存在しないことを言う。
極小元は複数存在する場合がある。
$\mathcal{K}$ が空でない有限集合の場合、極小元は必ず存在する^[1]。

テーブル

データベースにおけるテーブルの例として、以下のテーブルを考える。

社員ID	社員氏名	部署コード	部署名
1	社員A	2	部署Y
2	社員B	2	部署Y
3	社員C	1	部署X

テーブルには「社員ID」や「社員氏名」のような属性がある。属性全体の集合を $X$ としよう。
$X=\{\text{社員ID}, \text{社員氏名},\text{部署コード},\text{部署名}\}$ である。

各属性には型がある。例えば、社員IDは整数型、社員氏名は文字列型である。
各属性 $x\in X$ に対して、属性 $x$ の取りうる値の集合 $D(x)$ が考えられる。
例えば、$D(\text{社員ID})$ は整数の集合、$D(\text{社員氏名})$ は文字列の集合、のように考えられる。

テーブルには行がいくつかある。1行目を見ると、$(1, \text{社員A} , 2 , \text{部署Y})$ という行がある。ここでは行のことをタプルと呼ぶことにする。
タプルは写像 $X \to \bigcup_{x\in X} D(x)$ であると思うことができる。
例えば、1行目のタプルは次で定義される写像 $t\colon X \to \bigcup_{x\in X} D(x)$ である。

• $t(\text{社員ID})=1$
• $t(\text{社員氏名})=\text{社員A}$
• $t(\text{部署コード})=2$
• $t(\text{部署名})=\text{部署Y}$

ここで、直積 $\prod_{x\in X} D(x)$ を用いると、$t\in \prod_{x\in X} D(x)$ が成り立つ。
テーブルはタプルの集まりである。つまり、テーブルは $\prod_{x\in X} D(x)$ の部分集合と表現できる。

以上の話を踏まえて、テーブルを定式化する。

―――――――――
定義1 (テーブル)
$X$ を集合とし、$D = (D(x))_{x\in X}$ を集合族とする。$R \subseteq \prod_{x\in X} D(x)$ とする。
このとき、3つ組 $\langle X, D, R \rangle$ をテーブルと呼ぶ。単に $R$ のことをテーブルと呼ぶこともある。テーブルはリレーションとも呼ばれる。

$x\in X$ を属性と呼ぶ。また、$x\in X$ に対して、$D(x)$ を属性 $x$ のドメインと呼ぶ。
$t\in R$ を テーブル $R$ のタプルと呼ぶ^[2]。つまり、$R$ はタプルの集合である。

タプル $t\in R$ について、$t\in \prod_{x\in X} D(x)$ を満たす。さらに、$t$ は写像 $t: X \to \bigcup_{x\in X} D(x)$ である。

タプル $t\in R$、$A\subseteq X$ に対して、$t[A] = t|_A$ と表記する。
ただし、$t|_A$ は写像 $t$ の $A$ への制限であり、$t\colon X \to \bigcup_{x\in X} D(x)$ に対して、$t|_A\colon A \to \bigcup_{x\in X} D(x),\ t|_A(x) = t(x)$
と定義される。
―――――――――

$t[A] = t|_A$ という表記について、先程の例
$t\colon X \to \bigcup_{x\in X} D(x)$

• $t(\text{社員ID})=1$
• $t(\text{社員氏名})=\text{社員A}$
• $t(\text{部署コード})=2$
• $t(\text{部署名})=\text{部署Y}$

で確認する。
$t$ を表にすると以下のようになる。

社員ID	社員氏名	部署コード	部署名
1	社員A	2	部署Y

$A = \{\text{社員ID}, \text{社員氏名}\}$ としたとき、
$t|_A \colon A \to \bigcup_{x\in X} D(x)$
$t|_A(\text{社員ID})=1,\ t|_A(\text{社員氏名})=\text{社員A}$
である。
よって、$t[A](=t|_A)$ は タプル $t$ から $A$ にない属性の値を捨てて $A$ にある属性のみを残した、$t$ の部分タプルである。
$t[A]$ を表にすると以下のようになる。

社員ID	社員氏名
1	社員A

リレーションスキーマ

すべての $\prod_{x\in X} D(x)$ の部分集合（テーブル）が現実的なテーブルとは限らない。
例えば、以下のような「1つの部署コードに対応する部署名が複数ある」テーブルは普通現れない。
（以下のテーブルでは、部署コード4に対して、部署Wと部署Vの2種類が対応してしまっている）

社員ID	社員氏名	部署コード	部署名
4	社員D	3	部署Z
5	社員E	4	部署W
6	社員F	4	部署V

ここで、あり得るテーブル全体の集合として、$\prod_{x\in X} D(x)$ の部分集合の集合 $\mathcal{R} \subseteq \mathcal{P}(\prod_{x\in X} D(x))$ を考える。
テーブル $R \subseteq \prod_{x\in X} D(x)$ に対して、
$R\in \mathcal{R}$ であればあり得るテーブルと解釈し、$R \notin \mathcal{R}$ であればありえないテーブルと解釈する。

以上の話を踏まえて、リレーションスキーマを定義する。

―――――――――
定義2 (リレーションスキーマ)
$X$ を集合とし、$D = (D(x))_{x\in X}$ を集合族とする。また、$\mathcal{R} \subseteq \mathcal{P}(\prod_{x\in X} D(x))$ とする。このとき、3つ組 $\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマという。

$R\in \mathcal{R}$ はテーブルであり、とくにリレーションスキーマ $\langle X, D, \mathcal{R} \rangle$ のインスタンスと呼ぶ。
$\mathcal{R}$ はインスタンスの制約を表している。
―――――――――

テーブル（リレーション）が実際のデータなのに対して、リレーションスキーマはテーブルの設計に相当する。

関数従属性

テーブルに対する関数従属性の定義

「学生の所属する部活動と所属年数」のテーブルについて考える。

学籍番号	学生氏名	部活動	所属年数
1	学生A	部活動X	1
1	学生A	部活動Y	2
2	学生B	部活動X	2
3	学生C	部活動Y	1

このテーブルでは、属性について以下のことが言える。

• 学籍番号が決まれば学生氏名が決まる
• 学籍番号と部活動が決まれば、所属年数が決まる

このような関係を関数従属性という。関数従属性は次のように定義される。

―――――――――
定義3 (テーブルに対する関数従属性)
$\langle X, D, R \rangle$ をテーブルとする。
$\mathcal{P}(X)$ 上の二項関係 $\to_R$ を次のように定義する。
すなわち、$A, B \subseteq X$ に対して、$A \to_R B$ であることを
「$t_1, t_2\in R$ に対して $t_1[A] = t_2[A]$ ならば $t_1[B] = t_2[B]$」
と定義する。
$A\to_R B$ が成り立つことを「（テーブル $\langle X, D, R \rangle$ において）$B$ は $A$ に関数従属する」という。
$A\to_R B$ が成り立たないことを $A \not\to_R B$ と書くことにする。
―――――――――

「任意の $t_1, t_2\in R$ に対して $t_1[A] = t_2[A]$ ならば $t_1[B] = t_2[B]$」
であるというのは、「ある関数 $f$ が存在して、任意の $t\in R$ に対して $f(t[A]) = t[B]$ が成り立つ」ということである。

関数従属性の例をあげる。「学生の所属する部活動と所属年数」のテーブル $\langle X, D, R \rangle$ を考える。

学籍番号	学生氏名	部活動	所属年数
1	学生A	部活動X	1
1	学生A	部活動Y	2
2	学生B	部活動X	2
3	学生C	部活動Y	1

このテーブルにおいて、以下の関数従属性が成り立つ。

• $\{学籍番号\}\to_R\{学生氏名\}$
• $\{学籍番号, 部活動\}\to_R\{所属年数\}$

$\{学籍番号\}\to_R\{学生氏名\}$ という関数従属性は、「学籍番号が決まれば学生氏名が一意に決まる」ことを意味している。
また、$\{学籍番号, 部活動\}\to_R\{所属年数\}$ は、「学籍番号と部活動が決まれば所属年数が一意に決まる」ことを意味している。

このテーブルでは同姓同名がいないため、$\{学生氏名\}\to_R\{学籍番号\}$ が「たまたま」成り立っている。
もし同姓同名がいたら、$\{学生氏名\}\to_R\{学籍番号\}$ が成り立たないことになる。
このように、テーブルに対する関数従属性は、そのテーブルの状態によって成り立ったり成り立たなかったりする。

1つ極端な例を紹介する。
$\langle X, D, R \rangle$ をテーブルとし、$\lvert R\rvert = 0$ または $\lvert R\rvert = 1$ （テーブルのタプル数が0または1）とする。
このとき、任意の $A, B \subseteq X$ に対して、$A \to_R B$ が成り立つ。

証明

(1) $\lvert R\rvert = 1$ の場合
$A, B \subseteq X$ を任意に取る。$A \to_R B$ を示す。

$t_1, t_2\in R$ を任意にとる。$\lvert R\rvert = 1$ から $t_1 = t_2$ なので、
「$t_1[A] = t_2[A]$ ならば $t_1[B] = t_2[B]$」 が成り立つ。

以上から、$A \to_R B$ が成り立つ。

(2) $\lvert R\rvert = 0$ の場合
$A, B \subseteq X$ を任意に取る。$A \to_R B$ を示す。

$t_1, t_2\in R$ を任意にとる。「$t_1[A] = t_2[A]$ ならば $t_1[B] = t_2[B]$」が成り立たないと仮定する。
$R = \emptyset$ なので、$t_1\notin R$ であり、$t_1 \in R$ に矛盾する。
よって、「$t_1[A] = t_2[A]$ ならば $t_1[B] = t_2[B]$」が成り立つ。
（一般に「任意の $x\in \emptyset$ に対して $p(x)$ である」という形の主張は常に成り立つ。）

以上から、$A \to_R B$ が成り立つ。

つまり、テーブルのタプル数が0または1の場合は、すべての属性集合の間で関数従属性が成り立ち、もはや関数従属性の意味をなさない。

タプル数が0や1のように極端でなくても、タプル数が少ない場合には意図していない関数従属性が成り立ってしまうということがあり得る。
このように、ある特定のタイミングのインスタンス（テーブル）だけを見て関数従属性を考えると、そのテーブルの状態に大きく左右されてしまう。
そこで、リレーションスキーマのどんなインスタンスに対しても成り立つ関数従属性というものを考える。

リレーションスキーマに対する関数従属性の定義

―――――――――
定義4 (リレーションスキーマに対する関数従属性)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。$\mathcal{P}(X)$ 上の二項関係 $\to_\mathcal{R}$ を次のように定義する。
すなわち、$A, B \subseteq X$ に対して、$A \to_\mathcal{R} B$ であることを
「任意の $R\in \mathcal{R}$ に対して $A \to_R B$ である」
と定義する。

$A\to_\mathcal{R} B$ が成り立つことを「（リレーションスキーマ $\langle X, D, \mathcal{R} \rangle$ において）$B$ は $A$ に関数従属する」という。
$A\to_\mathcal{R} B$ が成り立たないことを $A \not\to_\mathcal{R} B$ と書くことにする。

誤解の恐れがなければ、$\to_\mathcal{R}$ を単に $\to$ と書く。
―――――――――

ここで、リレーションスキーマと関数従属性の例をあげる。
以下のテーブルをインスタンスに持つような「学生の所属する部活動と所属年数」のリレーションスキーマ $\langle X, D, \mathcal{R} \rangle$ を定義する。

学籍番号	学生氏名	部活動	所属年数
1	学生A	部活動X	1
1	学生A	部活動Y	2
2	学生B	部活動X	2
3	学生C	部活動Y	1

$X=\{学籍番号, 学生氏名, 部活動, 所属年数\}$ とする。
集合族 $D=(D(x))_{x\in X}$ を次のように定める。
すなわち $D(学籍番号), D(所属年数)$ を整数の集合、$D(学生氏名), D(部活動)$ を文字列の集合とする。
次に、インスタンスの制約 $\mathcal{R} \subseteq \mathcal{P}(\prod_{x\in X} D(x))$ を定める。兼部や同姓同名の可能性を考慮して次のように定義する。

$$\mathcal{R} = \left\{R \subseteq \prod_{x\in X} D(x) \mathrel{}\middle|\mathrel{} \begin{align*}\{学籍番号\}&\to_R\{学生氏名\} \\ \{学籍番号, 部活動\}&\to_R \{所属年数\}\end{align*} \right\}$$

このとき、$\langle X, D, \mathcal{R} \rangle$ は上記のテーブルをインスタンスとして持つリレーションスキーマである。
また、このリレーションスキーマについて、以下の関数従属性が成り立つ。

• $\{学籍番号\}\to_\mathcal{R}\{学生氏名\}$
• $\{学籍番号, 部活動\}\to_\mathcal{R} \{所属年数\}$

図で書くと、関数従属性は以下のようになる。

$\{学籍番号\}\to_\mathcal{R}\{部活動\}$ は成り立たない。
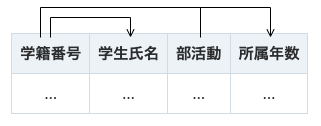
その理由を説明する。インスタンス $R\in\mathcal{R}$ として、兼部してる人がいる以下のインスタンスを考える。

学籍番号	学生氏名	部活動	所属年数
1	学生A	部活動X	1
1	学生A	部活動Y	2
2	学生B	部活動X	2
3	学生C	部活動Y	1

このインスタンス $R$ について、$\{学籍番号\}\to_R\{部活動\}$ は成り立っていない。
よって、$\{学籍番号\}\to_\mathcal{R}\{部活動\}$ は成り立たない。
同様に、同姓同名が発生しているインスタンスを考えることで、$\{学籍番号\}\to_\mathcal{R}\{学生氏名\}$ も成り立たないことがわかる。

関数従属性の性質

$X$ を属性全体の集合とする。 $\to$ を関数従属性を表す $\mathcal{P}(X)$ 上の二項関係とする。
（テーブル $\langle X, D, R\rangle$ に対する関数従属性 $\to_R$ でも、リレーションスキーマ $\langle X, D, \mathcal{R}\rangle$ に対する関数従属性 $\to_\mathcal{R}$でも良い）

$A,B,C \subseteq X$ とする。このとき、関数従属性について次の性質が成り立つ。

• $A\supseteq B$ ならば $A\to B$
• $A\to B$ ならば $A\cup C \to B\cup C$
• $A\to B$ かつ $B \to C$ ならば $A\to C$

また、上記3つの系として以下の性質もよく使用する。

• $A\supseteq B$ かつ $B \to C$ ならば $A \to C$
• $A\to B$ かつ $B \supseteq C$ ならば $A \to C$

完全関数従属

以下、関数従属性はリレーションスキーマに対する関数従属性のみを扱うことにする。
また $\to_\mathcal{R}$ を単に $\to$ と書くことにする。

―――――――――
定義5 (完全関数従属性)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
$A, B \subseteq X$ に対して、$A\to B$ を満たし^[3]、 $A$ が $\{A' \subseteq X \mid A'\to B\}$ の（包含関係における）極小元であるとき、$B$ は $A$ に完全関数従属するという。
関数従属するが完全関数従属しない場合は部分関数従属するという。
―――――――――

$B$ は $A$ に部分関数従属することは「ある $C \subsetneq A$ が存在して $C\to B$ が成り立つ」ことと同値である。

完全関数従属の例をとりあげる。
先程の「学生の所属する部活動と所属年数」のリレーションスキーマを例にする。

{学籍番号, 部活動}→{所属年数}という関数従属は完全関数従属である。
一方、{学籍番号, 部活動}→{学生氏名}という関数従属は部分関数従属である。
なぜならば、{学籍番号}→{学生氏名}という関数従属が成り立つからである。

キー

―――――――――
定義6 (スーパーキー)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
$A\subseteq X$ について、$A\to X$ が成り立つとき、$A$ をスーパーキーという。
―――――――――

―――――――――
定義7 (キー候補)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
$A\subseteq X$ が $\{A'\subseteq X\ \mid A'\text{はスーパーキー}\}$ の極小元であるとき、$A$ をキー候補という。
―――――――――

スーパーキーとは、スーパーキーでの値が決まればすべての属性の値が決まる（タプルが一意に定まる）属性集合のことである。
キー候補は極小のスーパーキーである。

$X$ はスーパーキーなので、$\{A'\subseteq X\ \mid A'\text{はスーパーキー}\} \neq \emptyset$ である。
よって、$X$ が有限集合であればキー候補は必ず存在する^[4]。
キー候補は複数存在する場合がある。

$A$ がキー候補であることは「$X$ が $A$ に完全関数従属する」と言っても同じことである。

$X$ が有限集合のとき、スーパーキーはあるキー候補のスーパーセット（キー候補を含む集合）である。

スーパーキー・キー候補の例をとりあげる。
先程の「学生の所属する部活動と所属年数」のリレーションスキーマを例にする。

{学籍番号, 部活動}はスーパーキーでキー候補である。また{学籍番号, 部活動}を含む属性の集合はスーパーキーである。
{学籍番号}はスーパーキーではない。なぜならば、（兼部の可能性から）{学籍番号}→{部活動}が成り立たないので、{学籍番号}→{学籍番号, 学生氏名, 部活動, 所属年数}が成り立たないからである。

正規形

正規形の目的

現実世界では、テーブルの値を更新したいという要望がある。
例えば、以下のテーブルで、「学籍番号」が1のタプル(1行目と2行目)に対して「学生氏名」を更新したいという話があり得る。

学籍番号	学生氏名	部活動	所属年数
1	学生A	部活動X	1
1	学生A	部活動Y	2
2	学生B	部活動X	2
3	学生C	部活動Y	1

この要望を定式化する。
リレーションスキーマ $\langle X, D, \mathcal{R}\rangle$ のインスタンス $R\in \mathcal{R}$ を考える。
$A\subseteq X, x\in X$ が $A\to_\mathcal{R} \{x\}$ という関数従属性を満たしているとする。
このとき「$t[A] = t_0$ となる $t\in R$ に対して、$t(c)$ の値を更新したい」（属性の集合 $A$ をアドレスとして属性 $x$ での値を更新したい）という話があり得る。

$L = \{t\in R \mid t[A] = t_0\}$ とする。ここでもし $\lvert L\rvert \geq 2$ の場合、2箇所以上のタプルを更新する必要が生じる。
複数箇所を更新するのは嫌なので、更新箇所は1箇所（$\lvert L\rvert= 1$）であってほしい（データベースの世界では1事実1箇所というスローガン（？）がある）。
もし、$A$ がスーパーキーであれば、$\lvert L\rvert \leq 1$ が成り立つ（$\lvert L\rvert \geq 2$ と仮定すると $A$ がスーパーキーであることに反する）。
逆に $A$ がスーパーキーでない場合は $\lvert L\rvert \geq 2$ となるようなインスタンス $R\in \mathcal{R}$ と $t_0$ が存在する。

以上から、$A\to_\mathcal{R} \{x\}$ という関数従属性が成り立っているならば、$A$ はスーパーキーであってほしい。
つまり、「$A$ がスーパーキーでないのに、$A\to_\mathcal{R} \{x\}$ という関数従属性が成り立ってる」という状況をできるだけなくしたい。
そういう状況を排除しようというのが、正規化である。正規化の段階として2NFや3NFなどがある。
2NFは、 $A\to_\mathcal{R} \{x\}$（$A$ は非スーパーキー）という関数従属性のうち、$A$ がキー候補の真部分集合である場合の関数従属性を排除（すなわち部分関数従属を排除）することを目的としている。

キー属性・非キー属性

2NF・3NFの定義には非キー属性という概念が現れるのでここで定義する。

―――――――――
定義8 (キー属性・非キー属性)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
$x\in X$ について、あるキー候補 $K\subseteq X$ が存在して $x\in K$ が成り立つとき、$x$ をキー属性という。
キー属性でない属性を非キー属性という。
―――――――――

2NFや3NFでは、「非スーパーキー→{非キー属性}」という関数従属性を排除する。
「非スーパーキー→{キー属性}」という関数従属性は2NFや3NFでは排除しない（この記事では扱わないが、3NFより制約の強いBCNFで排除する）。

2NF

―――――――――
定義9 (2NF)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
任意の非キー属性 $x\in X$、任意のキー候補 $K\subseteq X$ に対して、$\{x\}$ が $K$ に完全関数従属するとき、リレーションスキーマ $\langle X, D, \mathcal{R} \rangle$ は第2正規形(2NF, 2nd Normal Form)であるという。
―――――――――

$x$ が非キー属性で $K$ がキー候補の場合、$K \to \{x\}$ という関数従属性が成り立つ。この関数従属が完全関数従属であるというのが2NFの定義で述べられていることである。
2NFでないということは、ある非キー属性 $x$ があるキー候補 $K$ に部分関数従属するということである。
すなわち、非スーパーキー $A \subsetneq K$ が存在して、$A\to\{x\}$ という関数従属性が成り立つことになる。
（$A \subsetneq K$ から $A$ がスーパーキーでないことが言える。もし $A$ がスーパーキーならば $K$ がキー候補であることに矛盾する。）

2NFでない例をあげる。
「学生の所属する部活動と所属年数」のリレーションスキーマは2NFではない。

なぜならば、非キー属性「学生氏名」はキー候補{学籍番号, 部活動}に部分関数従属しているからである。それは{学籍番号}→{学生氏名}という関数従属があることからわかる。

この2NFでないリレーションスキーマは、2NFである2つのリレーションスキーマに分解できる。
具体的には、キー候補に部分関数従属している非キー属性「学生氏名」をリレーションスキーマから外し、新しく「学籍番号・学生氏名」を持つリレーションスキーマを作成することで、次に示す2NFのリレーションスキーマが2つできる。（リレーションスキーマの分解について、この記事ではこれ以上深く触れないことにする。）

学生番号	学生氏名
...	...

学生番号	部活動	所属年数
...	...	...

推移的関数従属性

次に3NFを定義するために推移的関数従属性を定義する。

―――――――――
定義10 (推移的関数従属性)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
$A\subseteq X$ と $x\in X$ に対して、ある $B\subseteq X$ が存在して、以下の(1)~(3)が成り立つとき、$\{x\}$ は $A$ に推移的関数従属するという。

(1) $A \to B \to \{x\}$
(2) $B \not\to A$
(3) $x\notin B$

$A\to \{x\}$ が成り立つが、推移的関数従属性が成り立たない場合は、$\{x\}$ は $A$ に非推移的に関数従属するという。
―――――――――

(1)の $A \to B \to \{x\}$ は 「$A\to B$ かつ $B \to \{x\}$」の略記である。

推移的関数従属性の定義の意味について説明する。「推移的」という言葉から(1)を求めることは自然である。(2)と(3)を求める理由を説明する。

まず(3) $x\notin B$ を求める理由を説明する。
(3)がない場合、（$\{x\} \not\to A$ を満たす）ただの関数従属 $A \to \{x\}$ がすべて推移的関数従属となってしまう。なぜならば、$B = \{x\}$ として考えると、$A \to \{x\} \to \{x\}$ が成り立つからである。「推移的」の意味を実現させるには(3)は不可欠である。
(文献によっては(3)がないが、(3)がないとこのように定義が壊れてしまう。)

次に(2) $B \not\to A$ を求める理由を説明する。
例として、「学生の所属する部活動と所属年数」のリレーションスキーマに、自動採番（オートインクリメント）されるIDを属性として追加したリレーションスキーマを考える

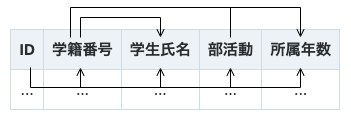
IDはタプルを一意に識別できる属性である。
キー候補は{ID}と{学籍番号, 部活動}である。
{ID}と{学籍番号, 部活動}の間には双方向の関数従属性
{ID}→{学籍番号, 部活動}, {学籍番号, 部活動}→{ID}が成り立つ。
ここで、もし条件(2)がない場合、{学籍番号, 部活動}→{所属年数}が推移的関数従属となってしまう。
なぜならば、{学籍番号, 部活動}→{ID}→{所属年数}だからである。
関数従属性{学籍番号, 部活動}→{所属年数}を推移的関数従属と言わないようにするために(2)の条件がある。

もう1つ、(2) $B \not\to A$ の意味を説明する。
(2)が成り立っていると、「$A$ がスーパーキーならば、$B$ はスーパーキーではない」という性質が成り立つ（後でこの性質を使う）。
もし(2)が成り立たず $B \to A$ が成り立っている場合、$A$ がスーパーキーならば $B$ はスーパーキーとなる。
(2)は $A$ がスーパーキーのときに、$B$ がスーパーキーにならないようにするための制約ともいえる。

3NF

推移的関数従属性を定義したので、3NFを定義する。

―――――――――
定義11 (3NF)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
次の条件(1), (2)を満たすとき、リレーションスキーマ $\langle X, D, \mathcal{R} \rangle$ は第3正規形(3NF, 3rd Normal Form)であるという。

(1) $\langle X, D, \mathcal{R} \rangle$ は2NFである。（任意の非キー属性 $x\in X$、任意のキー候補 $K\subseteq X$ に対して、$\{x\}$ が $K$ に完全関数従属する。）
(2) 任意の非キー属性 $x\in X$、任意のキー候補 $K\subseteq X$ に対して、$\{x\}$ が $K$ に非推移的に関数従属する。
―――――――――

後で証明するが、「(2)ならば(1)」が成り立つので、(1)の2NFであることは冗長である。しかし、「3NFならば2NFである」ことをわかりやすくするためか、このように定義されることが多い。
（3NFの原論文[1]では、この記事の「(1)かつ(2)」のように3NFを冗長に定義している。なお、文献[3]のように2NFを前提としない3NFの定義が書かれている文献もある。）

3NFも「非スーパーキー→{非キー属性}」という関数従属性を排除しようとしている。
3NFでなく特に(2)を満たさない状況はどういうことかを説明する。
(2)を満たさないとき、ある非キー属性 $x\in X$ とあるキー候補 $K\subseteq X$ が存在して、$\{x\}$ が $K$ に推移的関数従属するということである。
すなわち、ある $B\subseteq X$ が存在して、以下の条件を満たすということである。

• $K \to B \to \{x\}$
• $B \not\to K$
• $x \notin B$

$B \not\to K$ から、$B$ がスーパーキーで無いことがわかる（$B$ がスーパーキーならば $B\to K$ が成り立つので）。
ここで、関数従属性 $B \to \{x\}$ は「非スーパーキー→{非キー属性}」という関数従属性である。
3NFであれば $B \to \{x\}$ のような関数従属性がないことになる。
このように、3NFでも「非スーパーキー→{非キー属性}」という関数従属性を排除しようとしている。
2NFでは、関数従属性「非スーパーキー→{非キー属性}」のうち、非スーパーキーがあるキー候補の真部分集合でない場合の関数従属性については排除しなかった。
3NFでは、非スーパーキーがあるキー候補の真部分集合でない場合も含めて、「非スーパーキー→{非キー属性}」という関数従属性を排除している。

ここで3NFでない例を上げる。
以下に示す「社員の所属する部署」のリレーションスキーマを考える。

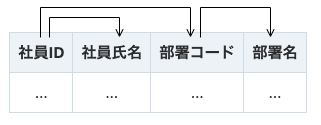
以下の関数従属性が成り立っているとする。

• {社員ID}→{社員氏名}
• {社員ID}→{部署コード}→{部署名}

キー候補は{社員ID}のみである。

このリレーションスキーマは（2NFではあるが）3NFではない。
なぜならば、{社員ID}がキー候補、「部署名」は非キー属性で、{社員ID}→{部署名}が推移的関数従属だからである（{社員ID}→{部署コード}→{部署名}という推移がある）。

もう1つ3NFでない例を上げる。
「学生の所属する部活動と所属年数」のリレーションスキーマは3NFではない。

先程見たとおり、このリレーションスキーマは2NFではないので、3NFではない。なお、「3NFの条件(2)を満たしていないから3NFでない」ということもできる。
なぜならば、キー候補{学籍番号, 部活動}と非キー属性「学生氏名」に対して、{学籍番号, 部活動}→{学生氏名}が推移的関数従属だからである（{学籍番号, 部活動}→{学籍番号}→{学生氏名}という推移がある）。
推移的関数従属{学籍番号, 部活動}→{学生氏名}は部分関数従属でもあった。
実は、「キー候補→{非キー属性}」という関数従属性は、部分関数従属であれば推移的関数従属であることが言える。後ほど証明する。

3NFの定義における2NFの冗長性

3NFの定義を再掲する。
―――――――――
定義11 (3NF・再掲)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
次の条件(1), (2)を満たすとき、リレーションスキーマ $\langle X, D, \mathcal{R} \rangle$ は第3正規形(3NF, 3rd Normal Form)であるという。

(1) $\langle X, D, \mathcal{R} \rangle$ は2NFである。（任意の非キー属性 $x\in X$、任意のキー候補 $K\subseteq X$ に対して、$\{x\}$ が $K$ に完全関数従属する。）
(2) 任意の非キー属性 $x\in X$、任意のキー候補 $K\subseteq X$ に対して、$\{x\}$ が $K$ に非推移的に関数従属する。
―――――――――

前に述べたが、(1)は冗長であり、「(1)かつ(2)」と(2)は同値である。すなわち「(2)ならば(1)」が成り立つ。

「(2)ならば(1)」を証明するために一つ補題を用意する。

―――――――――
補題12
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
$x\in X$ を非キー属性とし、$K\subseteq X$ をキー候補とする。
このとき、関数従属性 $K\to \{x\}$ が部分関数従属であれば、推移的関数従属である。
―――――――――

証明
関数従属性 $K\to \{x\}$ が部分関数従属であるとする。
このとき、ある $B \subsetneq K$ が存在して、$B\to \{x\}$ が成り立つ。
$K\to \{x\}$ が推移的関数従属であることを示すためには、以下を示せばよい。

• $K \to B \to \{x\}$
• $B \not\to K$
• $x \notin B$

[$K \to B \to \{x\}$ が成り立つこと]
$B \subsetneq K$ から $K \to B$ なので、$K \to B \to \{x\}$ が成り立つ。

[$B \not\to K$ が成り立つこと]
$K$ がキー候補であることから、$B \not\to K$ が成り立つ。もし、$B \to K$ が成り立ったら、$B$ がスーパーキーということになり、$B \subsetneq K$ であることから、$K$ がキー候補であること（スーパーキーの極小性）に矛盾する。

[$x\notin B$ が成り立つこと]
$B \subsetneq K$ であることから、$B$ の元はすべてキー属性である。$x$ は非キー属性なので、$x\notin B$ である。

以上から、$K\to \{x\}$ は推移的関数従属である。□

補題12は「キー候補→{非キー属性}」という関数従属性において「部分関数従属するならば推移的関数従属する」という話である。
一般の関数従属性では「部分関数従属するならば推移的関数従属する」が成り立つとは限らない点に注意である。

部分関数従属するが推移的関数従属しない例

属性全体を$X = \{x_1, x_2, x_3\}$ として、関数従属性 $\{x_1\} \to \{x_2, x_3\}$ が成り立つリレーションスキーマを考える。
関数従属性 $\{x_1, x_3\}\to \{x_2\}$ は部分関数従属だが、推移的関数従属ではない。

$\{x_1, x_3\}\to \{x_1\} \to \{x_2\}$ が成り立つことを考えると推移的関数従属ぽいが、$\{x_1\} \to \{x_1, x_3\}$ が成り立つので推移的関数従属とは言えない。

補題12の例として、3NFでない例であげたリレーションスキーマの関数従属性「{学籍番号, 部活動}→{学生氏名}」がある。
関数従属性「{学籍番号, 部活動}→{学生氏名}」は部分関数従属であり推移的関数従属という話をした。この話は補題12からも説明できる。

準備ができたので、3NFの定義における「(2)ならば(1)」を証明する。

―――――――――
定理13 (3NFの定義における2NFの冗長性)
$\langle X, D, \mathcal{R} \rangle$ をリレーションスキーマとする。
次の(1), (2)について、「(2)ならば(1)」が成り立つ。

(1) $\langle X, D, \mathcal{R} \rangle$ は2NFである。（任意の非キー属性 $x\in X$、任意のキー候補 $K\subseteq X$ に対して、$\{x\}$ が $K$ に完全関数従属する。）
(2) 任意の非キー属性 $x\in X$、任意のキー候補 $K\subseteq X$ に対して、$\{x\}$ が $K$ に非推移的に関数従属する。
―――――――――

証明
「(2)ならば(1)」の対偶「(1)でないならば(2)でない」ことを示す。
「(1)でないこと」と「(2)でないこと」は次のように書ける。

• (1)でない: ある非キー属性 $x\in X$と、あるキー候補 $K\subseteq X$ が存在して、$\{x\}$ が $K$ に部分関数従属する。
• (2)でない: ある非キー属性 $x\in X$と、あるキー候補 $K\subseteq X$ が存在して、$\{x\}$ が $K$ に推移的に関数従属する。

このことと補題12から「(1)でないならば(2)でない」が成り立つ。
つまり、「(2)ならば(1)」が成り立つ。□

以上で、3NFの定義において、2NFである条件が冗長であることが示された。

参考文献

• [1] Codd, Edgar F. "Further normalization of the data base relational model.". Data base systems 6. 1972, p33-64.
  • 2NFや3NFの原論文。
  • 2NFや3NFの定義は、今でも[1]にある定義が用いられる場合が多く、本記事でもこの定義をもとにして話を進めた。
    • 本記事の3NFと同様に、[1]の3NFの定義は「2NFでありさらに...」と冗長な定義になっている。
  • なお、[1]の推移的関数従属性の定義は不正確なので、代わりに[3]の定義を採用した。
• [2] Armstrong, William Ward. "Dependency Structures of Data Base Relationships." IFIP congress. Vol. 74. 1974.
  • アームストロングの公理の原論文。
  • タプルを写像として表現したり、タプル $t$ のサブタプルを $t|_A$ のように写像の制限を用いて表現したりするのは、この論文にも現れる。
  • この論文ではリレーションスキーマではなくテーブルに対して関数従属性を定義している。
• [3] Zaniolo, Carlo. "A new normal form for the design of relational database schemata." ACM Transactions on Database Systems (TODS) 7.3, 1982, p489-499.
  • 推移的関数従属の定義で参考にした。
  • この論文では3NFの定義に2NFを使用していない。そもそもこの論文に2NFが現れない。この論文で3NFの定義に2NFが不要なことを知った。
  • この論文ではテーブルに対する関数従属性を定義して、リレーションスキーマに対する関数従属性を定義している（本記事とほぼ同じである）
• [4] 石川 佳治：データベース1・2（2019年度）
  • 大学のデータベースの講義資料。
  • リレーションスキーマやインスタンスなどの用語、関数従属性の定義などを参考にした。
  • 関数従属性はリレーションスキーマに対して定義されている。
• [5] 集合論による関係データモデルの定式化 | Mathlog
  • 昔、筆者が書いた記事。
  • 本記事は記事[5]のリメイクのようなもの。
  • 記事[5]と本記事の主な違い
    • 記事[5]ではリレーションスキーマを定義せずテーブルで話を進めた。本記事ではリレーションスキーマを定義した。
    • 記事[5]ではテーブルに対して2NFを定義した。2NFなどの正規形はテーブルに対してではなくリレーションスキーマに対して定義されるべきだと考え、本記事ではリレーションスキーマで2NFを定義するように変更した。
    • 記事[5]では2NFは定義したが、3NFを定義してなかった。本記事では3NFも定義した。

脚注

1. $A_1\in \mathcal{K}$ を適当にとる。$A_1$ が極小元でない場合は、$\mathcal{K}$ の元で $A_1$ の真部分集合である $A_2$ が存在する。$A_2$ が極小元でない場合は、$\mathcal{K}$ の元で $A_2$ の真部分集合である $A_3$ が存在する。$\mathcal{K}$ が有限集合の場合、これを有限回繰り返すことで極小元が見つかる。

2. タプルはレコードとも呼ばれる。

3. $A$ が $\{A' \subseteq X \mid A'\to B\}$ の極小元ならば $A\to B$ を満たすので、$A\to B$という条件は冗長である。

4. 属性全体の集合 $X$ が無限集合のとき、キー候補が存在しない場合がある。例えば、$\mathbb{R}\to \mathbb{R}$ の連続関数全体のテーブルを唯一のインスタンスとして持つリレーションスキーマ$\langle \mathbb{R}, (\mathbb{R})_{x\in \mathbb{R}}, \{\{f\colon \mathbb{R}\to \mathbb{R} \mid f \text{は連続関数}\}\}\rangle$
   にはキー候補が存在しない。キー候補が存在しないことを簡単に説明する。
   このリレーションスキーマにおいて、$A\subseteq \mathbb{R}$ に対して、$A$ がスーパーキーであることと、$A$ が $\mathbb{R}$ において稠密であることは同値である（例えば $\mathbb{Q}$ はスーパーキーである）。このことから、$A$ がスーパーキーならば $x_0\in A$ に対して $A\setminus\{x_0\}$ もスーパーキーである（$A \neq \emptyset$ であることに注意）。よって、スーパーキー全体の極小元であるキー候補は存在しない（もし、キー候補 $A$ が存在したら $x_0\in A$ に対して $A\setminus\{x_0\}$ もスーパーキーなので $A$ の極小性に矛盾する）。