回帰についてまとめる
- 機械学習の文脈では教師あり学習の1つの分野
- 連続値をとる目的変数を予測するために使われる。
- 具体的な例として企業の今後数ヶ月間の売り上げを予測することなどが挙げられる。
線形回帰 (Linear Regression)
線形回帰の目標は1つ以上の特徴量と連続値の目的変数との関係をモデルとして表現すること。
単回帰(Simple Linear Regression)
線形回帰の中でも一つの特徴量(説明変数x)と連続値の目的変数(応答変数y)との関係をモデルとして表現することが単回帰の目的。
説明変数が一つだけの線形モデルの方程式は次のように定義できる。
ここで重み
ここでの目標は説明変数と目的変数の関係を表す1次式の重みを学習すること。
重みを学習することで、学習したデータセットに含まれていない新たなデータに対して値を予測することができる。
上記の1次式を前提とすれば、単回帰の場合には訓練データを通過する直線のうち最も適合するものを見つけ出すことと考えられる。
この最も適合する直線を回帰直線(regression line)と呼ばれ、回帰直線から訓練データへの縦線はオフセット(offset)または残差(residual)と呼ばれ、予測値の誤差を表す。
重線形回帰(Multiple Linear Regression)
複数の説明変数のバージョン。
単回帰と異なり説明変数が複数になるため、可視化が難しい。
データの理解
Exploratory Data Analysis
以下の2つを使ってデータを理解することで、どの変数を使って回帰による分析やモデルの作成を行えばいいかの判断をすることができる。
- 散布図行列
- 相関行列
散布図行列
散布図行列(ヒストグラムと散布図)を作成して、データセットの特徴量のペアに対する相関関係を可視化することができる。
mlxtendを使うことで簡単に散布図行列をプロットすることができる。
import matplotlib.pyplot as plt
from mlxtend.plotting import scatterplotmatrix
# 見やすさの観点から5つの列に限定する
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
# 散布図行列のプロット
scatterplotmatrix(df[cols].values, figsize=(10, 8), names=cols, alpha=0.5)
plt.tight_layout()
plt.show()
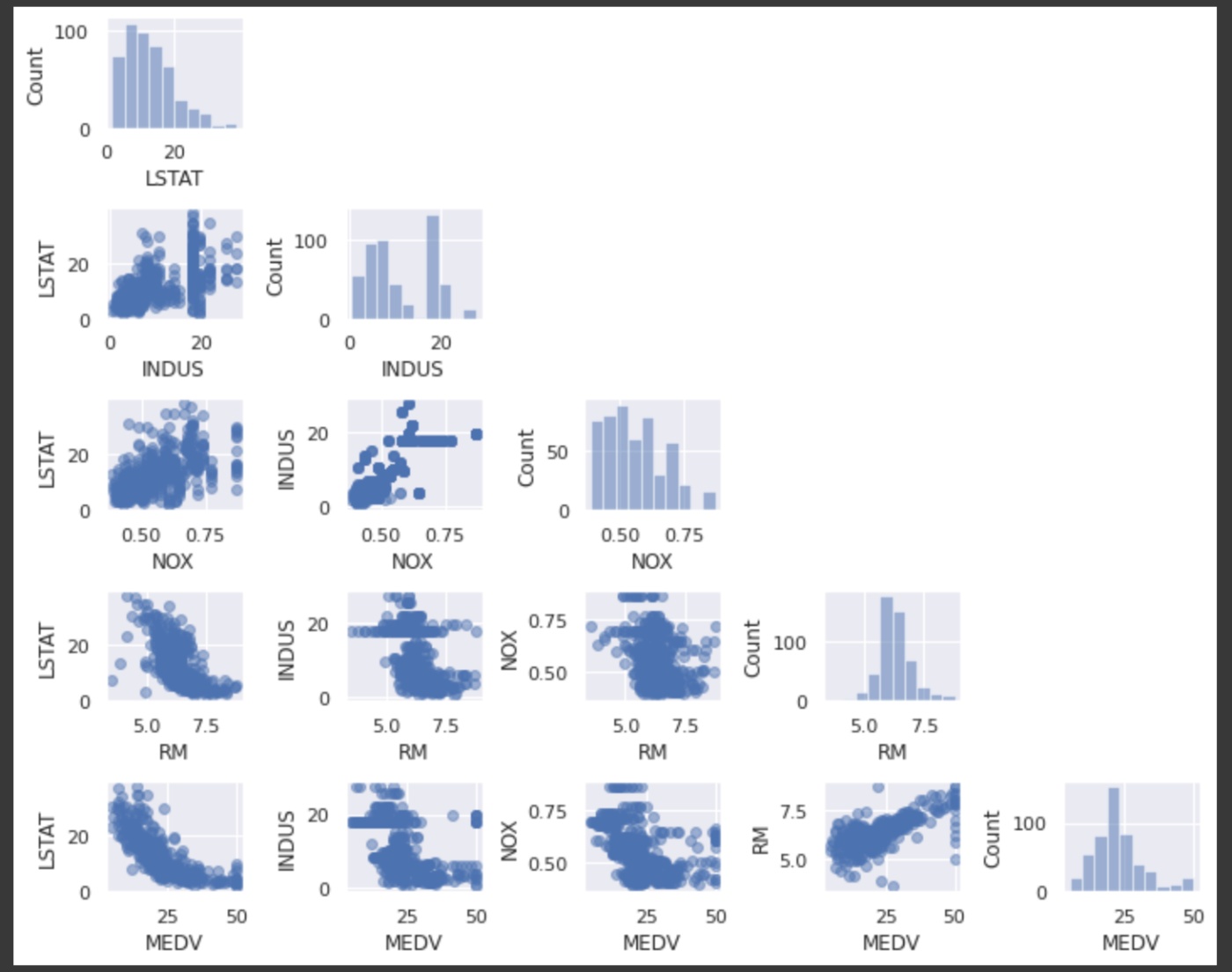
- RM(1戸あたりの平均部屋数)とMEDV(住宅価格の中央値)の関係は線形であることがわかる
- MEDVは正規分布に見えるが、いくつか外れ値がある
相関行列
変数の間の線形関数を数値化するために相関行列を作成する。
散布図行列と同様にmlxtendを使って簡単にプロットできる。
from mlxtend.plotting import heatmap
import numpy as np
cm = np.corrcoef(df[cols].values.T)
hm = heatmap(cm, row_names=cols, column_names=cols)
plt.show()
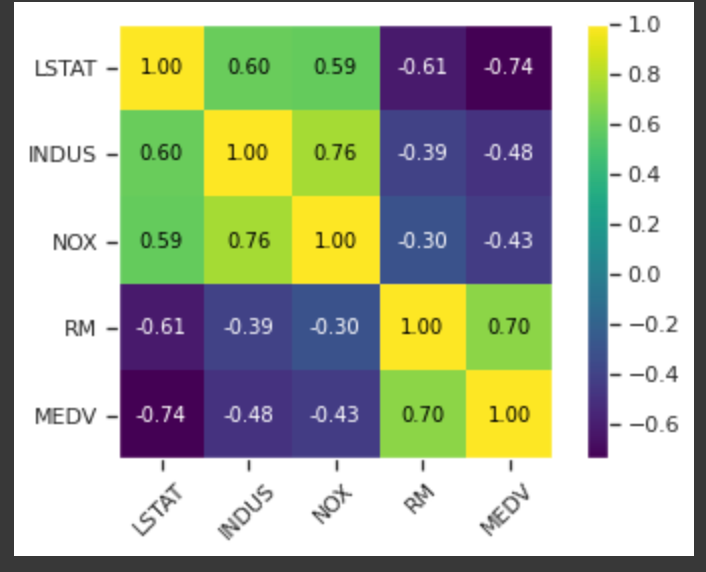
- 特徴量を選択するのに役立つ
- 線形回帰モデルを適合させるときに注目すべきは目的変数であるMEDVとの相関が高い特徴量
- LSTAT
- 上記の例だと最も相関が高いのは-0.74のLSTAT(低所得者の割合)であることがわかる。ただし、先程調べた散布図行列を見る限りこの2つの間には非線形の相関関係があることがわかる
- RM
- RM(1戸あたりの平均部屋数)とMEDVの相関も0.70で比較的高い。
- 先程の散布図行列からこの2つの間には線形の関係が成立することがわかり、単回帰分析に用いる説明変数としてうってつけに見える
pandasでの相関関係の把握
corr()ですべての変数間での相関関係(Standard Correlation Coefficient)が取得できる。
また、scatter_matrixで数値型の変数すべてのペアでの散布図を表示してくれる。(同じ変数同士の部分はhistogramを表示してくれる。
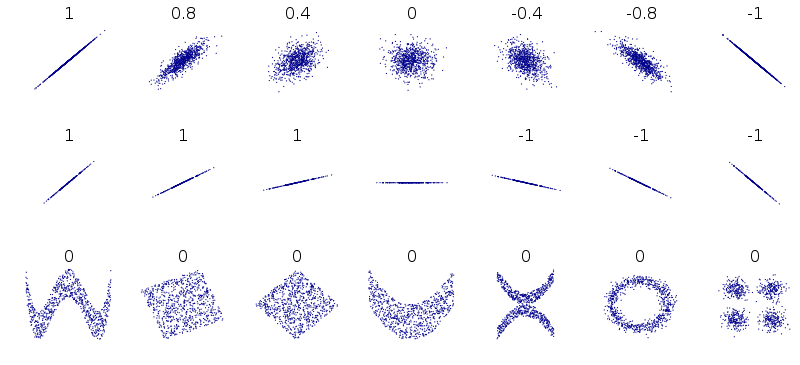
相関の注意点
- 非線形の関係はとらえられない
- 以下の図からわかるように一番下はcorrelation coefficientとしては0だが、明らかに2つの変数間になんらかの関係性がある
- 傾きは関係ない
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
モデルの構築
勾配降下法での実装
class LinearRegressionGD:
def __init__(self, eta=0.001, n_iter=20):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
# 予測値を取得
output = self.net_input(X)
# 正解データとの差分(誤差)を取る
errors = (y - output)
# 重みの更新
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
# コスト関数を計算して値をとっておく
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
# 総入力を計算する
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
return self.net_input(X)
上記のモデルを使ってHousingデータの住宅価格の平均値(MEDV)を予測してみる。
説明変数としては先ほどのデータの確認で線形の関係が確認できたRMを使う。
from sklearn.preprocessing import StandardScaler
X = df[['RM']].values
y = df['MEDV'].values
# Xとyの標準化を行う
sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
# scikit-learnの変換器ではインプットの形式として2次元を期待することが多い
# StandardScalerもそうであるため、np.newaxisで一時的に配列に次元を追加した後、
# flattenで1次元配列に戻す
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()
# モデルの学習
lr = LinearRegressionGD()
lr.fit(X_std, y_std)
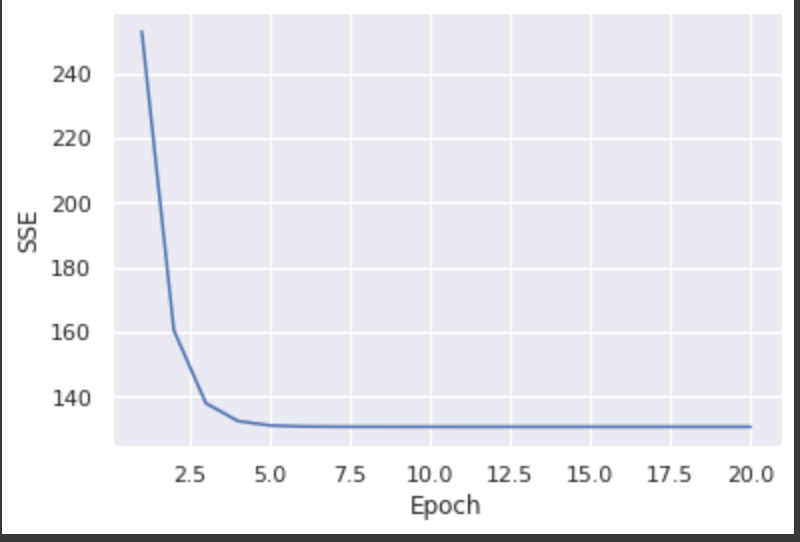
学習結果の確認
まず、コストが収束したことを確認するため、コストとエポック数の推移をプロットしてみる。
# コストの最小値に収束したことを確認するため
# コストをエポック数の関数としてプロットする
plt.plot(range(1, lr.n_iter+1), lr.cost_)
plt.xlabel('Epoch')
plt.ylabel('SSE')
plt.show()
次に訓練データに対してどれだけ適合しているかを確認するため、訓練データの散布図に回帰直線をプロットする。
# 線形回帰の直線がどれだけ訓練データに適合しているのかを確認する
# そのために訓練データの散布図をプロットし、回帰直線を追加する
def lin_regplot(X, y, model):
plt.scatter(X, y, c='steelblue', edgecolor='white', s=70)
plt.plot(X, model.predict(X), color='black', lw=2)
return None
lin_regplot(X_std, y_std, lr)
plt.xlabel('Average number of rooms [RM] (standardized)')
plt.ylabel('Price in $1000s [MEDV] (standardized)')
plt.show()
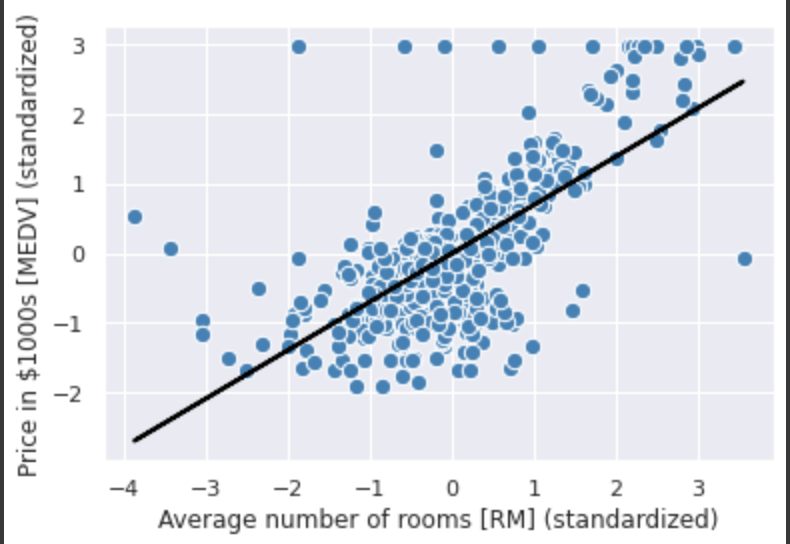
標準化前の結果を求める
標準化前の値が必要であれば、invers_transformを使う。
# テストのためにサンプルでインプットデータを作成
num_rooms_std = sc_x.transform(np.array([[5.0]]))
# サンプルデータを使ってモデルの予測を行う
price_std = lr.predict(num_rooms_std)
print('Price in $1000s: %.3f' % sc_y.inverse_transform(price_std)) # Price in $1000s: 10.840
scikit-learnでの実装
scikit-learnの回帰推定器の多くはSciPyの最小二乗法の実装(scipy.linalg.lstsq)を利用している。
このSciPyの実装はLAPACK(Linear Algebra PACKage)に基づく高度な最適化を利用している。
scikit-learnの線形回帰実装は確率的勾配降下法に基づく最適化を利用しないため、変数が標準化されていない方がうまくいく。
from sklearn.linear_model import LinearRegression
slr = LinearRegression()
slr.fit(X, y)
y_pred = slr.predict(X)
# 傾きの算出
print('Slope: %.3f' % slr.coef_[0])
# 切片の算出
print('Intercept: %.3f' % slr.intercept_)
標準化されていない変数を使って学習したため係数の値は異なるが、勾配降下法での実装と比較しても同様にデータにうまく適合していることが確認できる。
lin_regplot(X, y, slr)
plt.xlabel('Average number of rooms [RM] ')
plt.ylabel('Price in $1000s [MEDV] ')
plt.show()
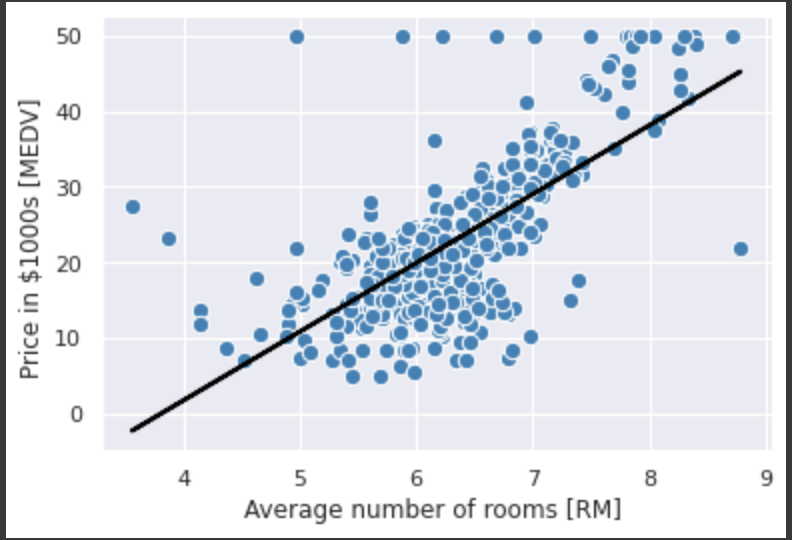
外れ値への対処
線形回帰モデルは外れ値の存在に大きな影響を受けることがある。
外れ値に対する対処法として以下の2つが挙げられる。
- 外れ値の除去
- RANSACアルゴリズムを使ったロバスト回帰
RANSACアルゴリズムを使ったロバスト回帰
ロバスト回帰(robust regression)とは外れ値の影響を抑えた上で回帰を実行する手法の総称。基本的なアイデアとしては外れ値の重みを小さくすることにある。
RANSACアルゴリズムは回帰モデルにデータのサブセット(いわゆる正常値)を学習させる。具体的な手順としては以下の通り。
- 正常値としてランダムな数のデータ点を選択し、モデルを学習させる
- 学習済みのモデルに対して、その他すべてのデータ点を評価し、ユーザ指定の許容範囲となるデータ点を正常値に追加する
- すべての正常値を使ってモデルを再び学習させる
- 正常値に対する学習済みモデルの誤差を推定する
- モデルの性能がユーザ指定のしきい値の条件を満たしている場合、又はイテレーションの数が既定回数に達した場合学習を終了する。そうでなければ1に戻る。
つまり、イテレーションの数と外れ値の許容範囲はユーザ側で指定する必要がある。
線形回帰モデルの性能評価
重回帰の場合には二次元のグラフとして描画することはできない。
しかし、予測された値に対する残差をプロットすることは可能である。
残差プロット
こうした残差プロットは回帰モデルを診断して非線形性や外れ値を検出し、誤差がランダムに分布しているかどうかをチェックするグラフィカルな解析に良く使われている。
予測が完璧な場合には残差はちょうど0になる。
現実のモデルで残差がゼロになることはまずないが、良い回帰モデルでは誤差がランダムに分布し、中央の直線周辺にランダムに散らばるはず。
逆に残差プロットにパターンが見られる場合は、モデルがなんらかの説明情報を捕獲できていないことを意味する。
残差プロットの算出
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
# 残差プロット
plt.scatter(y_train_pred, y_train_pred - y_train,
c='steelblue', marker='o', edgecolor='white',
label='Training data')
plt.scatter(y_test_pred, y_test_pred - y_test,
c='limegreen', marker='s', edgecolor='white',
label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, color='black', lw=2)
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('images/10_09.png', dpi=300)
plt.show()
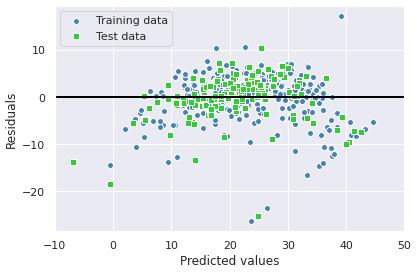
平均二乗誤差(Mean Squared Error)
モデルの性能を数値化するもう一つの効果的な手法が平均二乗誤差。
さまざまな回帰モデルの比較や、グリッドサーチと交差検証を通じたパラメータのチューニングに役立つ。
ただし、分類の正解率とは対照的にMSEが最適解ではないことに注意が必要。MSEの解釈はデータセットと特徴絵用のスケーリングに依存するため、単純な比較はできない?
そのため、場合によっては決定係数を求める方が有益かもしれない
算出
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
print('MSE train: %.3f, test: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
>>>
MSE train: 22.545, test: 21.517
R^2 train: 0.743, test: 0.711
RMSE
誤差の幅に重みをつけたもの。
正解データから大きく外れるほど誤差を多く取る。
外れ値が多い場合にはMSEの方が適しているケースも
決定係数
決定係数はモデルの性能をより効果的に解釈するために標準化されたMSEと考えることができる。
回帰に正則化手法を用いる
正則化は過学習の問題に対処する手法の一つであり、モデルの極端なパラメータの重みにペナルティを課すための追加情報を導入する。
正則化された線形回帰のアルゴリズムとしては以下の3つが一般的に使われる。
- リッジ回帰(Ridge Regression)
- LASSO(Least Absolute Shrinkage and Selection Operator)
- Elastic Net法
リッジ回帰(Ridge Regression)
L2ペナルティ付きのモデル。
LASSO
L1ペナルティ付きのモデル。
Elastic Net法
リッジ回帰とLASSOの折衷案。
L1ペナルティとL2ペナルティの両方を使う。
L1ペナルティは疎性を作成するために使われ、L2ペナルティはm > nの場合に特徴量をn個よりも多く選択するために使われる。
多項式回帰: 非線形に対応する
scikit-learnでのサンプル実装
scikit-learnに多項式回帰のモデルが用意されているわけではないが、PolynomialFeaturesを使って多項式の特徴量を生成し、それに対して単回帰のモデルを適用することで多項式回帰が実現できる。
コードとしては以下の通り。
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
X = np.array([258.0, 270.0, 294.0,
320.0, 342.0, 368.0,
396.0, 446.0, 480.0, 586.0])\
[:, np.newaxis]
y = np.array([236.4, 234.4, 252.8,
298.6, 314.2, 342.2,
360.8, 368.0, 391.2,
390.8])
# 線形回帰(最小二乗法)モデルのクラスをインスタンス化
lr = LinearRegression()
pr = LinearRegression()
# 2次の多項式特徴量のクラスをインスタンス化
quadratic = PolynomialFeatures(degree=2)
X_quad = quadratic.fit_transform(X)
# 単回帰モデルの学習
lr.fit(X, y)
# np.newaxisで列ベクトルにする
X_fit = np.arange(250, 600, 10)[:, np.newaxis]
# 予測値を計算
y_lin_fit = lr.predict(X_fit)
# 多項式回帰のため、変換された特徴量で重回帰モデルを学習する
pr.fit(X_quad, y)
# np.newaxisで列ベクトルにする
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))
# 単回帰と多項式回帰の結果をプロット
plt.scatter(X, y, label='Training points')
plt.plot(X_fit, y_lin_fit, label='Linear fit', linestyle='--')
plt.plot(X_fit, y_quad_fit, label='Quadratic fit')
plt.xlabel('Explanatory variable')
plt.ylabel('Predicted or known target values')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
グラフを見ると多項式回帰の方が線形回帰よりもデータの特徴をうまく捉えていることがわかる。
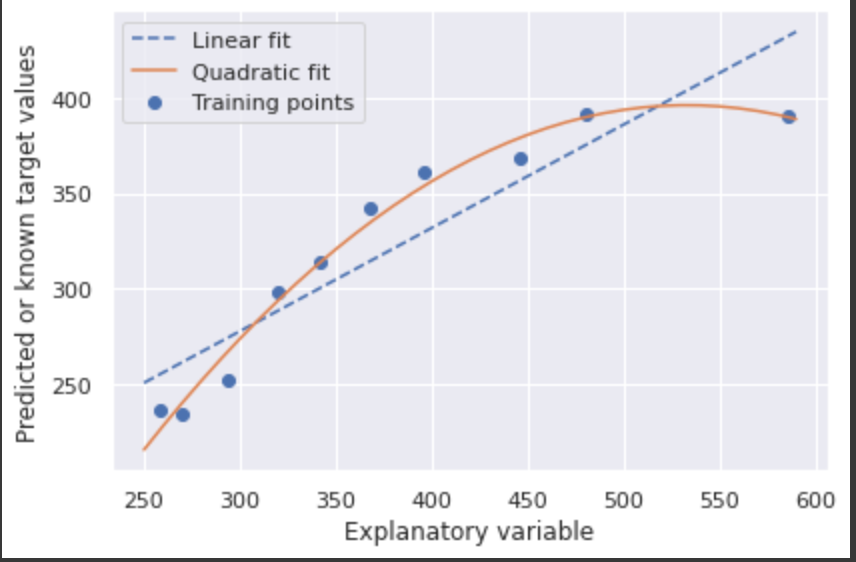
評価指標としてMSEと
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)
print('Training MSE linear: %.3f, quadratic: %.3f' % (
mean_squared_error(y, y_lin_pred),
mean_squared_error(y, y_quad_pred)))
print('Training R^2 linear: %.3f, quadratic: %.3f' % (
r2_score(y, y_lin_pred),
r2_score(y, y_quad_pred)))
>>>
Training MSE linear: 569.780, quadratic: 61.330
Training R^2 linear: 0.832, quadratic: 0.982
Housingデータセットでの実装
Housingデータセットに多項式回帰を適用してみて、線形回帰との違いをみてみる。
X = df[['LSTAT']].values
y = df['MEDV'].values
regr = LinearRegression()
# 2次と3次の特徴量を生成
quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)
X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis]
# 特徴量の学習、予測、決定関数の計算
regr = regr.fit(X, y)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y, regr.predict(X))
# 特徴量の学習、予測、決定関数の計算
regr = regr.fit(X_quad, y)
y_quad_fit = regr.predict(quadratic.fit_transform(X_fit))
quadratic_r2 = r2_score(y, regr.predict(X_quad))
# 特徴量の学習、予測、決定関数の計算
regr = regr.fit(X_cubic, y)
y_cubic_fit = regr.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, regr.predict(X_cubic))
# plot results
plt.scatter(X, y, label='Training points', color='lightgray')
plt.plot(X_fit, y_lin_fit,
label='Linear (d=1), $R^2=%.2f$' % linear_r2,
color='blue',
lw=2,
linestyle=':')
plt.plot(X_fit, y_quad_fit,
label='Quadratic (d=2), $R^2=%.2f$' % quadratic_r2,
color='red',
lw=2,
linestyle='-')
plt.plot(X_fit, y_cubic_fit,
label='Cubic (d=3), $R^2=%.2f$' % cubic_r2,
color='green',
lw=2,
linestyle='--')
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000s [MEDV]')
plt.legend(loc='upper right')
plt.show()
グラフからわかるように3次や2次の多項式回帰モデルの方が線形回帰よりも2つの変数の関係をよく表していることがわかる。
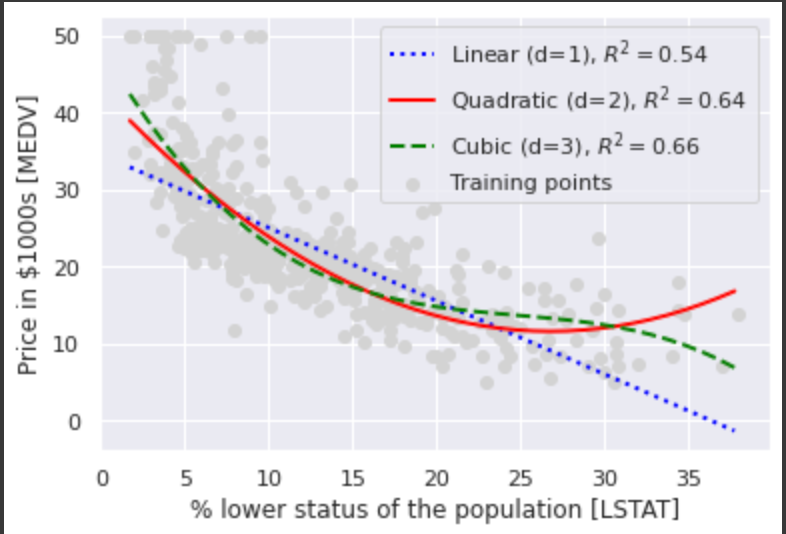
ただし、注意点として多項式の特徴量を追加するほどモデルの複雑さが増すため過学習の可能性が高まる。
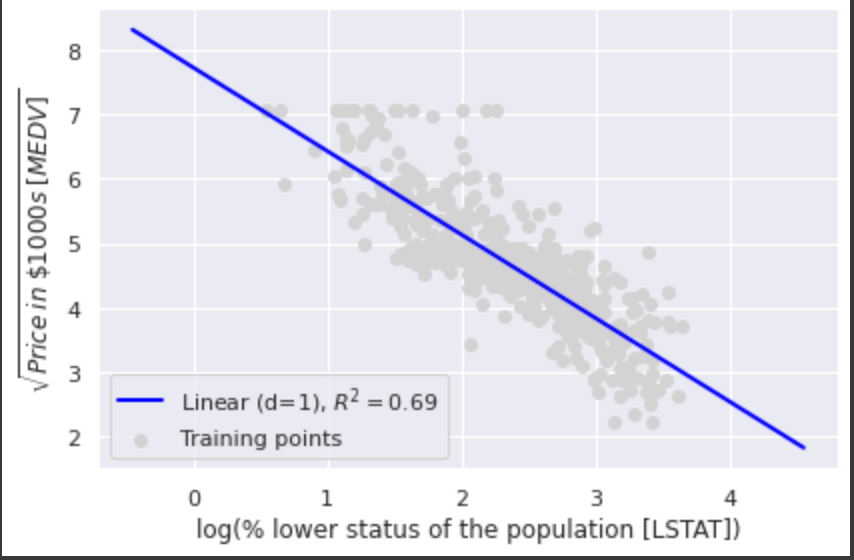
また、上記の注意点に加えて、非線形回帰をモデル化する手法として多項式の特徴量が必ず最良の選択とは限らない。
例えば上記の例では2つの変数の関係性を別の線形特徴量空間に変換(射影)することが考えられる。
以下の例では2つの変数間の関係が
X = df[['LSTAT']].values
y = df['MEDV'].values
# 特徴量を変換
X_log = np.log(X)
y_sqrt = np.sqrt(y)
X_fit = np.arange(X_log.min()-1, X_log.max()+1, 1)[:, np.newaxis]
# 変換したデータを線形回帰で学習、予測
regr = LinearRegression()
regr = regr.fit(X_log, y_sqrt)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y_sqrt, regr.predict(X_log))
# 回帰直線をプロット
plt.scatter(X_log, y_sqrt, label='Training points', color='lightgray')
plt.plot(X_fit, y_lin_fit,
label='Linear (d=1), $R^2=%.2f$' % linear_r2,
color='blue',
lw=2)
plt.xlabel('log(% lower status of the population [LSTAT])')
plt.ylabel('$\sqrt{Price \; in \; \$1000s \; [MEDV]}$')
plt.legend(loc='lower left')
plt.tight_layout()
#plt.savefig('images/10_13.png', dpi=300)
plt.show()
R2のスコアからわかるように多項式回帰を使った際のスコア(0.66)よりデータにうまく適合している。
Random Forestを使った非線形関係に対する対処
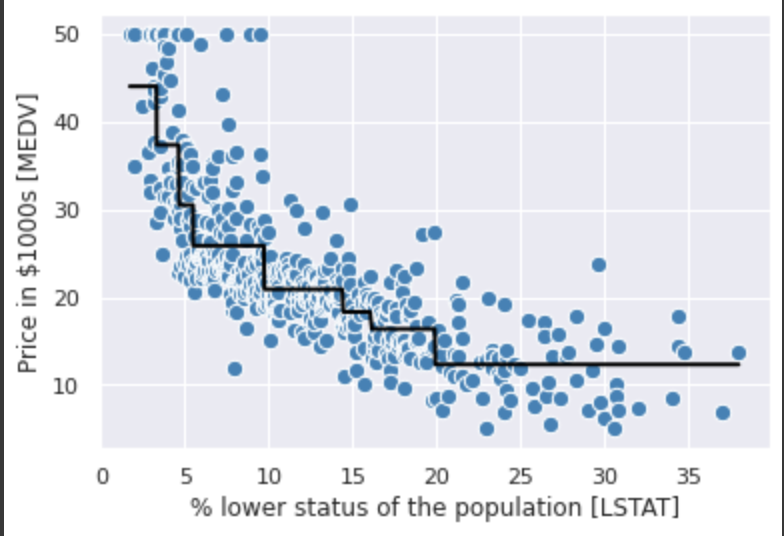
Decision Tree(決定木)
2つの変数間の関係をDecision Tree Regressorを使って学習してみる。
from sklearn.tree import DecisionTreeRegressor
X = df[['LSTAT']].values
y = df['MEDV'].values
tree = DecisionTreeRegressor(max_depth=3)
tree.fit(X, y)
sort_idx = X.flatten().argsort()
lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000s [MEDV]')
#plt.savefig('images/10_14.png', dpi=300)
plt.show()
グラフからわかるように、関係性をうまく捉えてはいるが、DecisionTreeの特性として予測値が連続ではないという制約がある。
Random Forest
最後にRandom Forestのモデルですべての特徴量を使って学習してみる。
from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=1)
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=1000,
criterion='mse',
random_state=1,
n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
>>>
MSE train: 1.641, test: 11.056
R^2 train: 0.979, test: 0.878
結果からわかるように現在のモデルは過学習の傾向にある。(それでもtestセットでのR2スコアは高い傾向にあり、目的変数と説明変数の関係はよく捉えられている)
残差をプロットしてみると誤差はランダムに分布しておらず、一定のパターンが見られる。
plt.scatter(y_train_pred,
y_train_pred - y_train,
c='steelblue',
edgecolor='white',
marker='o',
s=35,
alpha=0.9,
label='Training data')
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='limegreen',
edgecolor='white',
marker='s',
s=35,
alpha=0.9,
label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='black')
plt.xlim([-10, 50])
plt.tight_layout()
plt.show()
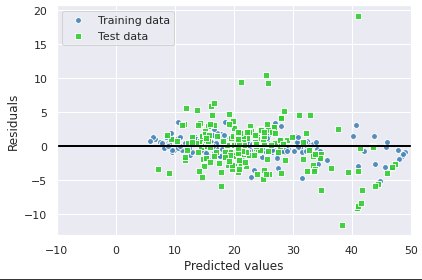
残差プロットの非ランダム性に対処する普遍的な対応策はないため、以下のような対応を実験するしかない。
- 変数を変換する
- ハイパーパラメータをチューニングする
- より単純、または複雑なモデルを選択する
- 外れ値を取り除く
- 特徴量を追加する
参考資料
実例()
statsmodelsを使って回帰分析を行ってみる。
概要
データセットとしては以下を使用する。
顧客の情報とマーケティングのメールに対して反応したかどうかのデータが含まれている。
前処理
目的変数がYes、Noという値で設定されているため、1と0に変換を行う。
# 反応したかどうか(目的変数)を0と1に変換する
df['Engaged'] = df['Response'].apply(lambda x: 0 if x == 'No' else 1)
モデルの学習
continuous_vars = [
'Customer Lifetime Value', 'Income', 'Monthly Premium Auto',
'Months Since Last Claim', 'Months Since Policy Inception',
'Number of Open Complaints', 'Number of Policies',
'Total Claim Amount'
]
import statsmodels.api as sm
# Output variablesと説明変数を渡す
logit = sm.Logit(
df['Engaged'],
df[continuous_vars]
)
# 学習を行う
logit_fit = logit.fit()
# 学習結果のサマリーを表示する
logit_fit.summary()
以下のように説明変数ごとの相関関係などが確認できる。
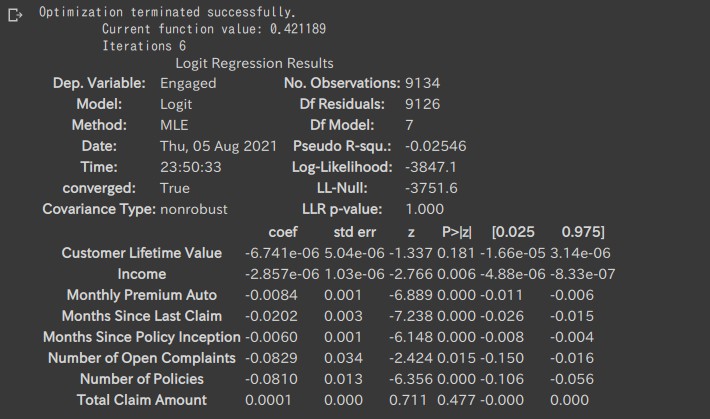
-
coefは係数(Coefficient。説明変数が被説明変数に与える影響)を示す -
zはz-score(平均が0、標準偏差 (SD) が1になるように変換した得点。標準偏差の数が母平均より上または下である度合いのこと) -
P>|z|はp-value(簡単に言うとその値になることが偶然である確率)を表す。低ければ低いほど、その結果の確度が高い(単なる偶然ではない)ことを示す。
例えばNumber of Policiesはp-valueの値から有意な結果であると考えられ、なおかつ、coefがマイナスなので、Number of Policiesが高いほどマーケティングの施策に反応しなくなることを示唆する。
このようにp-valueとcoefficientの値からRegression Analysisの結果を解釈できる。