AlphaZeroでオセロ実装 - alpha-rebrew

はじめに

この記事は、一関高専 Advent Calendar 2024の記事です。
また丁度いいので、「今年の最も大きなチャレンジ」の記事としても投稿致します。

AlphaZero でオセロを実装する中で、だいたい半年間 Web 上に上がっている記事や論文を参考に自分なりの工夫を繰り返し、強化学習の基本概念の習得や機械学習のスクリプトの組み方などを習得することが出来ました。

Zenn を見渡すと素晴らしい功績の数々が投稿されており、先行事例の多いオセロの実装なんて趣味の範疇を出ない小さな取り組みに思えますが、僕個人としてはとても有意義な個人開発だったと感じております。

という訳で、この記事では「オセロの AI を AlphaZero で実装したお話」について記述します。
拙文ですが、読んでいただけると嬉しいです。

リポジトリの命名

https://github.com/Oya-Tomo/alpha-rebrew-py

名前は、「alpha-rebrew」です。

プログラムを書いていくにあたって、ネット上の記事を一通り漁りました。
AlphaZero でオセロを作るのは先行事例が沢山存在したので、N 番煎じという意味を込めrebrewを名前に付けました。

事前学習

AlphaZero の実装について調べる前に、強化学習の手法について一通り学習を行いました。

データサイエンス初心者の味方、AIcia Solid Project です。YouTube の再生リストを添付します。
筆者はこの動画を何周もしました。

https://www.youtube.com/playlist?list=PLhDAH9aTfnxI1OywfnxXCDTWGtYL2NxJR

全部は記述しないので、キーワードを列挙しておきます。

• 環境
• エージェント
• 状態 → 行動 → 報酬
• 状態価値関数・行動価値関数
• ベルマン方程式

AlphaZero について

強化学習について動画で勉強した後、AlphaZero での実装方法を中心にアルゴリズムや既存の手法と比較した特徴について調査を行いました。

PV-Net

AlphaZero の脳みそと言うべき、深層学習モデルはとても特徴的な構造をしています。
PV-Net の P は Policy(方策)を表し、V は Value(価値)を表します。
このニューラルネットは、入力として State(状態)を取り、出力として Policy(方策)と Value(価値)を返却します。

Policy(方策)

環境はエージェントに対して、State(状態) と現状取れる Action(行動)を提供します。
Policy とは、与えられた複数の行動の中からエージェントが特定の行動を選択する確率のことです。

方策は、関数で $\pi(s, a)$ のように表されます。状態$s$のときに行動$a$を選択する確率を表します。

PV-Net では、これらの方策値を取りうるすべての Action に対して推論・出力します。
そのため、出力は以下の配列になります。

$$[\pi(s, a_{00}), \pi(s, a_{01}), \pi(s, a_{02}), \cdot\cdot\cdot , \pi(s, a_{76}), \pi(s, a_{77}), \pi(s, a_{pass})]$$

※ Action は式中で $a_{yx}$の形式で記載しています。$x,y$は盤面の座標です。$(0 \le x \le 7, 0 \le y \le 7)$
※ $\pi(s, a_{pass})$ はパスの方策値を表します。

Value(価値)

現在の盤面から終盤面まで 1 エピソード終わったときに得られる合計報酬の期待値です。

オセロ、将棋、チェス、囲碁などのゲームの場合、エージェントはゲーム終了時に勝敗に応じた報酬を 1 度だけ受け取ります。
そのため、エージェントに学習させる Value は、ゲーム終了時の報酬を教師データとして使用します。

モデルの実装

筆者の実装では CNN(Res-Net)を内部で使用しています。
入力では、盤面を[黒石, 白石, 置ける場所]のレイヤーに整形して入力します。入力の形状としては RGB 画像と同じです。
出力は、Policy が 65 個 (64 手 + パス) の数値、Value が 1 個の数値です。分かりやすいようにサンプルのデータを以下に示します。

# input
state =[
    [
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 1, 0, 0, 0,],
        [0, 0, 0, 1, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
    ],
    [
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 1, 0, 0, 0, 0,],
        [0, 0, 0, 0, 1, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
    ],
    [
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 1, 0, 0, 0, 0,],
        [0, 0, 1, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 1, 0, 0,],
        [0, 0, 0, 0, 1, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
        [0, 0, 0, 0, 0, 0, 0, 0,],
    ],
]

# output
policy = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.3, 0.0, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.2, 0.0, 0.0, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.0, 0.0, 0.2, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.0, 0.3, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
          0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
          0.0
          ]
value = [0.0]

エージェントの行動選択

AlphaZero のアルゴリズムを調べる中で、筆者はここの理解に一番時間がかかりました。
実際にコードを読んでもらうのが早いと思います。

AlphaZero は、モンテカルロ木探索を用いて行動を選択します。
モンテカルロと言いつつ、実際にはランダム性は殆どありません 💦
ほんの少し Policy にディリクレノイズを加えるくらいです。
この探索を通じて、PV-Net の推論した Policy と Value を基に、より正しい Policy を生成します。

探索

盤面の木探索は、しばしば再帰的に行われます。
以下の式を各ノードで計算し、最も高い $Score$ を持つ行動を選択します。

$$C(s) = log\frac{1 + N(s) + C_{base}}{C_{base}}+C_{init}$$

$$U(s, a) = C(s)P(s, a)\frac{\sqrt{N(s)}}{1 + N(s, a)}$$

$$Q(s, a) = \frac{S(s, a)}{N(s, a)}$$

$$Score = argmax_a ( Q(s, a) + U(s, a) )$$

• $C(s)$ : 過去の探索をもとに出した事前確率をどれくらい探索に反映させるかの重み
  実装では定数にされている例が多かった。
• $U(s, a)$ : 探索回数が少ないノードを優先的に探索するための項
  探索回数が多くなると、この項は事前確率として影響してくる。
• $Q(s, a)$ : 盤面$s$において行動$a$を選択したときの報酬の平均値

木が保持する情報としては以下の 3 つがあります。

• N(s) : 盤面sに訪れた回数
• N(s, a) : 盤面sに対して行動aを選択した回数
• W(s) : 盤面s以下を探索したときの推定報酬の合計
• V(s) : 盤面sの価値 (PV-Net で推論した Value or 終盤面の評価値)
• P(s) : 盤面sに対する Policy

筆者の実装だと各ルート盤面に対して、探索を 800 回くらい行います。
盤面の探索が進むにつれて、木に多くの探索結果が蓄積されていきます。
木は 1 エピソードが終わるたびにリセットされます。

出力

探索が終了したら、探索木の訪問回数から Policy を生成します。
方策値の各要素を数式で表すと以下のようになります。新しい方策という意味で $\pi'$ と表記します。

$$\pi'(s, a) = \frac{N(s)}{N(s, a)}$$

探索結果として出力するのは、配列なので上の数式を全ての Action に対して適用します。

$$[\pi'(s, a_{00}), \pi'(s, a_{01}), \pi'(s, a_{02}), \cdot\cdot\cdot , \pi'(s, a_{76}), \pi'(s, a_{77}), \pi'(s, a_{pass})]$$

※ Action は式中で $a_{yx}$の形式で記載しています。$x,y$は盤面の座標です。$(0 \le x \le 7, 0 \le y \le 7)$
※ $\pi'(s, a_{pass})$ はパスの方策値を表します。

行動の選択

探索結果から、最も高い Policy を持つ行動を選択します。
$argmax_a\{\pi'(s, a)\}$ です。

モデルの学習プロセス

AlphaZero のアルゴリズムは、主に 2 つのフェーズの繰り返しによってモデルを強化します。
それぞれのフェーズで行われていることを紹介します。

セルフプレイ

このフェーズでは、PV-Net を組み込んだエージェントが黙々と自分同士で対戦をします。
ここで生成した対戦情報を、データセットにState, Policy, Valueとして保存しておきます。

• State : 盤面
• Policy : 探索によって計算された盤面に対する方策
• Value : エピソード最終盤面に得られた報酬

なお、エージェントは各盤面に対して探索を行い生成した、新しい方策に基づいて行動を選択します。

学習

このフェーズでは、生成したデータセットをランダムな順番に並べ替えてひたすら学習します。
データセットをそのままの順番で使うと時系列性が残ってしまうため、それを破壊します。

学習の過程で古くなった過去のデータは、定期的に削除されます。

コーディング

一通り AlphaZero について調べた後実際にコードを書いていく段階に入りますが、僕がやりたかった事をそのまま実装している方がいらっしゃいました。

https://horomary.hatenablog.com/entry/2021/06/21/000500

探索のコードについては特に、この記事を結構参考にさせていただきました。あざます!!

とはいえ、オセロの環境やモデルの実装、データの整形やセルフプレイなど結構手を加えています。

環境

強化学習の環境として、オセロの盤面を実装しました。もちろん Bitboard です。

https://gist.github.com/Oya-Tomo/f1ddc97d26fefc0334e7207d771f0433

何を思ったのか、勢いで Rust でも Bitboard を実装していました。

https://gist.github.com/Oya-Tomo/bc208b4f832ff6c7b10332144717a30e

モデル

AlphaZero で必要な PV-Net は Pytorch で実装しました。アーキテクチャは以下のようになっています。
レイヤーのハイパーパラメータなどは、リポジトリを参照して下さい。

良いのか悪いのか評価を行っておりませんが、ResNet のブロックを 3 つ積み重ね、最後に Policy と Value に分岐する構造になっています。
モデルの、特に ResBlock の部分の構造は、試行錯誤しています。詳しくは、フィードバックの章で述べます。

データ整形

モデルに入力するデータは、盤面を 3 チャンネルに分割して入力します。

• 自身の石
• 相手の石
• 置ける場所

このデータを Pytorch の Tensor に変換して入力します。
入力テンソルのチャンネルの順番で、ターンを区別しています。

教師データは、Policy と Value を用意します。
Policy は探索結果から生成した方策を使用します。
Value は、エピソードの最終盤面の報酬を使用します。

この報酬を何にするかが、探索や学習の結果に大きく影響します。
先に述べておくと、初期の報酬は勝敗をそのまま 1,0,-1 としていましたが、最終的には盤面の石数の差を報酬として使用しました。

マルチプロセス化

Python は GIL というものがあるため、マルチスレッドはあまり効果がありません。
そのため、マルチプロセス化を行いました。
はじめは、ray を使用していましたが、最終的には pytorch の multiprocessing を使用しています。
セルフプレイでのモデルの推論と盤面の展開に時間がかかるため、CPU と GPU を効率的に回してくれるのが学習高速化にとても効果的でした。

フィードバック

ここまで一通り実装を行い、学習ループを回してみると、いくつかの問題点が見えてきました。
それらを以下に詳しく記述します。

石数が探索に影響しない

AlphaZero は、原論文では囲碁や将棋などの勝ちと負けしか無いゲームを対象にしています。
そのため Web に上がっているサンプルも、それに習っているものが多いです。

しかしオセロの場合は、なるべく多くの石を取ることが勝利に繋がります。
そのため石数の差を報酬として使用することで、なるべく多くの石を取るように学習を行いました。

また、勝敗のみを報酬として使用すると、報酬の関数が微分不可能になってしまうため、連続値に近い報酬にする目的もありました。

勝敗のみを報酬とした場合の関数 👆

Value の 0 寄り

次に、Value の報酬を盤面の石数の差に変更しました。
しかし、今度は学習ループを数時間回した時点で Value の推論値が 0 に寄っていることが分かりました。
これでは、正しい探索を行うことが出来ません。

この原因を考えるために、筆者は Value の分布が正規分布に似た形になっているのではないかと仮定しました。
オセロの報酬は、モデルへの入力時に -1 から 1 の範囲に正規化されます。そのため、仮定した分布もだいたいの最大値と最小値を合わせています。

正規分布 (平均 : 0, 標準偏差 : 0.3)👆

これを教師データにするとなると、分布が 0 付近に偏っていて適切ではないと考え Value の報酬を変形する関数を考えました。

Value の分布を変形

Value の報酬を変形する関数を考えるため、筆者は Tanh 関数を使用しました。
ただし、ただの Tanh ではなく、定数 $a$ の調整も行います。

$$f(x) = \frac{e^{ax} - x^{-ax}}{e^{ax} + x^{-ax}}$$

$a$を 3 に設定した場合のグラフを以下に示します。

だいたい、x=1 付近で y=1.0 になるように設定しました。

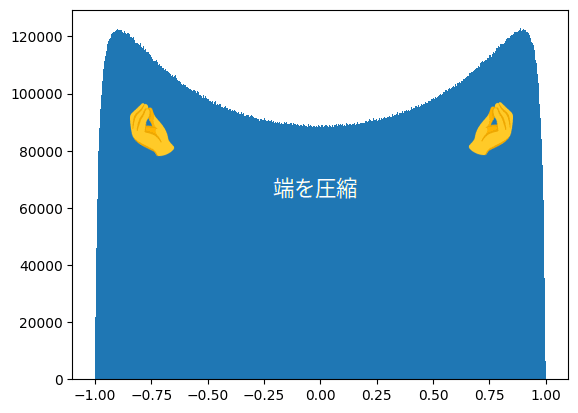
この関数を通した、分布を以下に示します。

変形した分布は、中央付近が少し凹んだ形になっています。
この変形によって得られる主な効果は、以下の 2 つです。

推論値の散らばりへの効果

上のヒストグラムを参照すると分かる通り、この変形によって Value の教師データは 1 または -1 付近の値が若干多くなります。
こうすることで、モデルの推論値が 0 に寄らず、以前よりも散らばりを持つようになりました。

loss への効果

Tanh 関数を使用した変形によって、接戦状態での盤面の推論値の loss を大きくすることが出来ます。以下は、実際に計算してみた例です。

モデルの学習時、Value 値の loss は MSE で計算されます。
この loss は、推論値と教師データの差の 2 乗の平均です。

例えば、石の数が黒 34, 白 30 の盤面で、黒が勝っているという教師データがあるとします。
エージェントは、この盤面に対して黒 30, 白 34 と推論したとします。
モデルの予測からすれば小さな違いですが、ゲームの勝敗としては全く真逆です。

変形前の報酬計算式を以下に示します。

$$Value_{before} = \frac{black - white}{black + white}$$

この場合、Value の loss は以下のように計算されます。
正解の Value は $(34 - 30) / 64 = 0.0625$ です。
推論値は $(30 - 34) / 64 = -0.0625$ です。
loss は $(0.0625 - (-0.0625))^2 = 0.015625$ です。

次に、変形後の報酬計算式を以下に示します。

$$Value_{after} = tanh(\frac{black - white}{black + white}, a=3)$$

この場合、Value の loss は以下のように計算されます。
正解の Value は $tanh(0.0625, a=3) = 0.1853$ です。
推論値は $tanh(-0.0625, a=3) = -0.1853$ です。
loss は $(0.1853 - (-0.1853))^2 = 0.137344$ です。

この例では、loss が約 8.8 倍になりました。

このように、Value の推論値を変形することで、接戦状態での loss を大きくし、接戦状態の盤面推論でモデルがミスしたときのペナルティを重くすることができます。

また、そんなに精度の必要ない圧勝・完敗の盤面に対しては Value の loss を小さくすることが出来ます。

僕の頭の中のイメージはこんな感じです。

モデルのアーキテクチャの検討

PV-Net の大きさや性能はエージェントの行動の精度に直結するため、モデルのアーキテクチャについても何度も検討を行いました。
モデルの肥大化は記憶容量と引き換えに推論速度を犠牲にします。
ここらへんは、使用できる推論リソースや推論対象となる問題の複雑さによって変わってくるため、一概にどちらが良いとは言えません。今思えば、もう少し小さくても良かったかも... 💦

このアーキテクチャの検討について、一部では Common Layers を使用しないで、Policy と Value を分けた方が性能が出るのではないかという意見もありましたが、今回は検証を行っていません。次の機会に検証してみたいです。

セルフプレイの初期盤面をランダム生成

これは、先行事例として行っている人が複数いたため取り入れてみました。
エージェントは、行動選択の過程で基本的に価値の高い行動を選択するため、初期盤面が同じだと同じような対局が続いてしまいます。これを防ぐため、初期盤面をランダム生成するようにしました。
初期のランダム手数は、0 ~ 58 手の範囲でランダムに設定しています。

結果

最終的に、フィードバックで述べた改善を行い、学習を行いました。
学習環境は、研究室のデスクトップ PC をお借りして行いました。ありがとうございました!!
GPU は NVIDIA GeForce RTX 3060 です。

学習結果が楽しみ過ぎて、毎日朝と晩に 1 回ずつ対戦を行いました。
結果は、1 ~ 3 日間は全然でしたが、4 ~ 5 日目になると徐々に学習の成果を実感するようになり、1 週間以上回し続けると、筆者との対戦で約 80%の確率で勝利するようになりました。

余談ですが、筆者はオセロの AI に勝つために、スマホでトレーニングしていました。
そうしたら、もともとレベル 20 にも勝てなかった筆者が、レベル 60 に勝てるようになりました。
アプリの AI のレベルがどれほどかは分かりませんが、結構すごいことではないかと感じています。
結論→ 筆者が強化学習した。

所感

AlphaZero の調査・実装を通して、長所や短所を調べたり感じたりしたことを少しまとめて見ようと思います。
まず長所としては主に 3 つ考えられます。
1 つ目は 、Policy と Value を同時に学習することで、モデルに対して教師を複数用意することができる点です。PV-Net の Common Layers では、Policy と Value の共通の特徴を学習することができるため、モデルの学習効率が向上するのではないかと考えられています。
2 つ目は、モンテカルロ木探索による行動選択では、より報酬の高い盤面を優先的に探索することが出来るように設計されている点です。価値の低い盤面に対しての草刈りが必要ない点は素晴らしいと感じました。
そして 3 つ目は、様々なゲームに応用がきく点です。状態に対して取れる行動の個数が、コンピューターのリソース的に保持できる数ならばとても有用な手法だと考えます。

一方で、短所としては、オセロのような比較的単純なゲームに対しては、探索の無駄なランダム性が存在するということです。
将棋などのような、複雑かつ勝敗しか報酬の与えようがないゲームに対しては、ランダム性があり、積極性のある探索はとても有効な手法です。
しかし、オセロの場合は、理論的には終盤面からの逆算で報酬の計算が可能なため（計算リソースを無視）MiniMax 法や AlphaBeta 法の方が適すると言われています。
この点に関しては、実装を行ったことがないので詳しく言及することは出来ませんが、オセロ AI 世界 1 位の egaroucid の技術記事を見て、「確かに」と感じることが多々ありました。

https://www.egaroucid.nyanyan.dev/ja/technology/

今回の実装では、AlphaZero での実装を目的として行いましたが、次回以降は、MiniMax 法や AlphaBeta 法の実装にも挑戦してみたいと思います。

謝辞

この記事を書くにあたり、ご協力いただきました皆様に感謝いたします。

• mriki 先生 : 実装にあたって、学習環境の提供、アドバイスをいただきました。
• Aisia Solid Project 様 : 勝手に参照させていただきました。