Ray Tracing from Scratch in Rust ~ 簡易CPUレンダラの自作と仕組みの勉強 ~

はじめに

皆さんこんにちは，一関高専 村上研究室所属 小山田です。

今回は，Ray Tracingの基礎的な仕組みを学ぶために，自作した簡易CPUレンダラについて紹介します．
筆者は，CGの分野とはあまり縁がなかったのですが，最近は3Dシミュレーションを行うことが多いため，実は結構気になっていた分野ではありました．
制作を進める中で，どこがそんなに時間のかかる処理なのか，RTコアの無いGPUはなんでシミュレーションが若干重いのかなど，気になっていた疑問を少しだけ解消できたように思います．

この制作を行う上で，GitHub CopilotとAIをゴリゴリに使っていますし，論文も何も追っていません．
しかし，基礎的な仕組みを理解した気になれる記事になっていると思いますので，興味のある方は是非読んでみて下さい．

なお，これで作成した制作物は，現在筆者が受講しているCGの授業の課題制作として提出予定です😎
制作物 ↓↓↓
https://github.com/Oya-Tomo/build_your_own_raytracer

ここからは宣伝です．
今年も，記事の文頭にこれが沢山載る季節になりましたね．そうです，アドカレです．
この記事は，一関高専の学生で書いているAdvent Calender 2025の11日目の記事となります．
是非，他の記事もご覧ください !
https://adventar.org/calendars/12218

追記: Rust Advent Calendar 2025 のシリーズ2 13日目にも登録しました．
Rust信者が増えますように🙏
https://qiita.com/advent-calendar/2025/rust

Ray Tracingとは

n番煎じ感が否めませんが，解説します．
Ray Tracingとは，光線(ray)の追跡(tracing)を行うことで，3Dシーンのレンダリングを行う手法です．
従来のレンダリング手法であるラスタライズ法では，3Dシーンを2D画像に変換する際に，ポリゴンをピクセルに変換する過程で，光の反射や屈折，拡散などの複雑な現象を正確に表現することが難しいという問題がありました．
一方，Ray Tracingでは，光の経路をシミュレートすることで，これらの現象をよりリアルに表現することが可能となります．

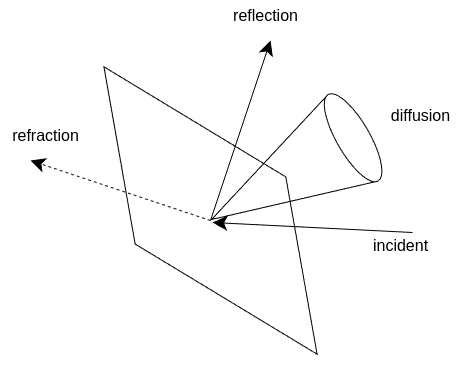
ここからの処理は，基本的に以下の流れで行われます．

1. Rayの生成 (カメラからシーンに向けてRayを発射)
2. Rayの追跡
   1. 面との交差判定
   2. 反射・屈折・拡散したRayを再度追跡
   3. これを一定の深さまで繰り返す
3. Rayの色の計算 (光を初期のRayへ逆伝搬)

なお想像がつくと思いますが，Rayは非常に大量に発射され，途中で分岐もするため，計算量が膨大になります．
$N$個のRayと$M$個の面の交差判定は，単純計算で$O(N \times M)$と表せ，さらに反射・屈折・拡散などでRayが莫大に増えるため最終的な計算量も爆発的に増加します．

この問題を解消するため，BVHなどの空間分割アルゴリズムが用いられ，木構造を辿ることで交差判定の計算量を削減します．
因みに，BVHで用いられるBounding BoxとRayの交差判定を高速に並列で行うのがRTコアの主な役割です．
参考: Bounding Volume Hierarchy (BVH) の実装 - 構築編

しかし，今回の制作では最適化を一切行わず，単純な全探索(再帰関数)で交差判定を行っていますので，結構重いです．
一つ，筆者の疑問としてあるのは，再帰関数的な処理をGPUで高速化するのはどうやっているのか，という点です．
ループを展開するのは可能だと思いますが，それでもかなり複雑な処理になると思います．
やはり，ゲームエンジンを作ってくれている先人に感謝ですね...🙏

Rayの実装

Rayは，始点(origin)と方向(direction)を持つベクトルとして実装します．
なお光の色はRayの逆伝搬の際に計算するため，Ray自体は色を持ちません．

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/mod.rs#L16-L38

Rayの生成

Rayの生成は，カメラからシーンに向けて行います．
カメラは，位置(position)，方向(direction)，上方向(up)，画角(fov)を持ち，縦横の幅(width, height)からRayを生成します．

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/camera.rs#L8-L114

計算としては，以下の順番で行います

1. カメラの方向ベクトルと垂直で距離が1離れた仮想画面を仮定し，その画面の右方向(right)と上方向(up)を計算

外積を取ることで，$v_{forward}$と$v_{up}$に垂直なベクトルを計算
$v_{right} = v_{forward} \times v_{up}$

再度外積を取って，$v_{forward}$と$v_{right}$に垂直なベクトルを計算
$v_{up}' = v_{right} \times v_{forward}$

※入力のupベクトルは画面の上方向と一致しない場合があるため再計算

2. 仮想画面の幅と高さを計算

縦画角(fov)から，仮想画面の高さ$h$を計算
$h = 2 \times \tan(fov / 2)$

仮想画面の幅$w$を計算
$w = w_{pix} \times h / h_{pix}$
※$w_{pix}, h_{pix}$はピクセル数

3. 各ピクセルに対応するRayを生成

各ピクセル$(i, j)$に対して，カメラからのRayを生成

画面の中心を原点とした座標系で，[-0.5, 0.5]の範囲に正規化
$u = (i + 0.5) / w_{pix} - 0.5$
$v = (j + 0.5) / h_{pix} - 0.5$

仮想画面上の位置を計算 (左上が原点，右方向が正，下方向が正の画面座標系)
$v_{direction} = v_{forward} + u \times w \times v_{right} - v \times h \times v_{up}'$

Anti-Aliasing

各ピクセルに対して一つのRayを生成するだけでは，画像がギザギザになってしまうためAnti-Aliasingを行います．
各ピクセルを更に細かいサブピクセルに分割し，各サブピクセルに対してRayを生成します．
処理としては，$0.5$の部分を更に細かく分割したオフセット値$o_x, o_y$を用いて，以下の計算に置き換えます．

$u = (i + o_x) / w_{pix} - 0.5$
$v = (j + o_y) / h_{pix} - 0.5$

Rayと面の交差判定

今回の実装では，基本的な球体(sphere)と三角形(triangle)の2種類の面との交差判定を実装しています．

球体との交差判定

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/sphere.rs#L49-L94

まず，Rayの始点を$O$，方向(長さは1)を$D$，Rayの長さを$t$，球体の中心を$C$，半径を$r$とします．

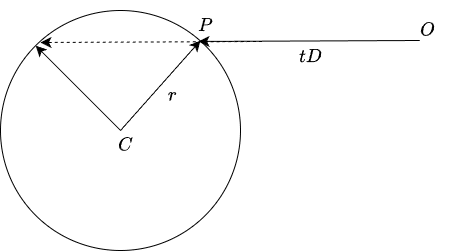
このとき，Ray上の点$P$は以下のように表されます．この式から，$t$の解を求めることで交差判定を行います．

$$P = O + tD = C + r$$

この式を変形すると，以下の2次方程式が得られます．

$$\| O + tD - C \|^2 = r^2$$

ノルムの2乗を展開すると内積で計算できるため，スカラを係数にもつ$t$の2次方程式として表せます．

$$(O + tD - C) \cdot (O + tD - C) = r^2 \\ D \cdot D t^2 + 2D \cdot (O - C) t + (O - C) \cdot (O - C) - r^2 = 0$$

あとは，係数を以下のように設定し，解の公式と判別式を用いて，$t$の解を求めます．

$$\begin{align} a &= D \cdot D \notag \\ b &= 2D \cdot (O - C) \notag \\ c &= (O - C) \cdot (O - C) - r^2 \notag \end{align}$$

最後に，$t$の実数解が存在する場合，交差していると判定し，0以上かつ最小の$t$を交差点までの距離として利用します．

$$t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

三角形との交差判定

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/mesh.rs#L101-L147

交差判定にはMöller–Trumboreアルゴリズムを用います．

まず，Rayの始点を$O$，方向(長さは1)を$D$，Rayの長さを$t$とします．
また，三角形の頂点を$v_0, v_1, v_2$とし，辺ベクトルを$e_1 = v_1 - v_0, e_2 = v_2 - v_0$とします．

そして，交差判定を行う前に，三角形とRayが平行でないかを確認します．
式としては，以下のように表されます．

$$det = e_1 \cdot (D \times e_2)$$

ここで$D$と$e_2$の外積を計算しますが，もし$D$が$e_1, e_2$を含む平面に平行であれば，外積は面の法線ベクトルとなります．
そのため，$e_1$との内積が0となり，交差しないと判定できます．

因みに，スカラー三重積の循環性から，以下のように書き換えることもできます．
筆者的には，面の法線ベクトルとRayの方向ベクトルの内積を求めている，こちらの式の方がイメージしやすかったです．

$$det = D \cdot (e_2 \times e_1)$$

そして次に，Rayと三角形を含む面との交点$P$は以下のように表されます．
この式には，$t, u, v$の3つの未知数が含まれています．これらのパラメタを求めることで，交差判定を行います．

$$P = O + tD = v_0 + u e_1 + v e_2$$

最初に，$S = O - v_0$と置くと，以下の式が得られます．
以下の式には，$e_1, e_2, D, S$などのベクトルが含まれているので，$t, u, v$を求めるためのそれぞれの式を立てるために，内積を使って他の成分を消去していきます．

$$S = u e_1 + v e_2 - tD$$

1. $u$を求める

両辺を$D \times e_2$と内積を取ります．(右からかける)
そうすると，$e_2, D$の成分が消去され，$u$の式が得られます．

$$u = \frac{S \cdot (D \times e_2)}{det}$$

2. $v$を求める

両辺を$e_1 \times D$と内積を取ります．(右からかける)
そうすると，$e_1, D$の成分が消去され，$v$の式が得られます．

$$v = \frac{D \cdot (S \times e_1)}{det}$$

3. $t$を求める

両辺を$e_2 \times e_1$と内積を取ります．(右からかける)
そうすると，$e_1, e_2$の成分が消去され，$t$の式が得られます．

$$t = \frac{e_2 \cdot (S \times e_1)}{det}$$

最後に，$u, v, t$の値を用いて交差判定を行います．交差の条件は以下の通りです．

• $t$が0以上であること (交点がRayの始点より前にない)
• $0 \leq u \leq 1 \land 0 \leq v \leq 1 \land u + v \leq 1$ (交点が三角形の内部にある)

Rayの分岐

Rayが面と交差したタイミングで，反射・屈折・拡散などの処理を行い，新たなRayを生成します．

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/raytracer.rs#L94-L193

Rayの追跡による色の計算は再帰的に行なわれるため，初めに終了条件を設定します．
なお，終了条件に合致した場合，背景色を返すようにしています．

• 再帰の深さが一定値に達した場合
• カメラから出たRayへの寄与が非常に小さくなった場合
• Rayが面や光源と交差しなかった場合

分岐処理には，Rayと面の法線ベクトルから，次に生成するRayの方向を決定します．

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/raytracer.rs#L272-L374

反射

反射は，入射角と等しい角度でRayが跳ね返る現象です．
反射ベクトル$R$は，以下の式で計算されます．

$$R = D - 2 N (D \cdot N)$$

入射ベクトルの$D$を，法線方向と接線方向の成分に分解し，法線方向の成分を反転させるイメージです．

$$\begin{align} D_\perp &= N(D \cdot N) \notag \\ D_\parallel &= D - D_\perp \notag \\ R &= D_\parallel - D_\perp = D - 2 D_\perp \notag \end{align}$$

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/raytracer.rs#L361-L371

屈折

屈折は，Rayが異なる媒質に入る際に，進行方向が変化する現象です．
屈折の方向は，スネルの法則に基づいて計算されます．
まず，入射角$\theta_i$と屈折角$\theta_t$の関係は以下の式で表されます．
参考: https://www.optics-words.com/kogaku_kiso/snells-law.html

$$\eta = \frac{n_i}{n_t} = \frac{\sin \theta_t}{\sin \theta_i}$$

次に，屈折角が90度を超える場合，全反射が発生するため，それについても考慮します．
以下の式が成り立つ場合，全反射は発生しません．

$$\sin \theta_t = \eta \sin \theta_i \leq 1$$

このとき，$sin \theta_t$を求めるのが難しいため，以下のように変形します．

$$\sin^2 \theta_t = \eta^2 \sin^2 \theta_i = \eta^2 (1 - \cos^2 \theta_i) \leq 1 \\$$

そして，屈折ベクトルが存在することが確認できたら，以下の手順で導出することができます．

反射と同じく，入射ベクトル$D$を法線方向と接線方向の成分に分解します．

$$\begin{align} D_\perp &= N(D \cdot N) = - \cos \theta_i N \notag \\ D_\parallel &= D - D_\perp = D + \cos \theta_i N \notag \end{align}$$

次に，接線方向の成分を屈折率に基づいてスケーリングして，屈折後の接線方向の成分$T_\parallel$を計算します．

$$T_\parallel = \eta D_\parallel = \eta (D + \cos \theta_i N) \\$$

そして，法線方向の成分$T_\perp$を計算します．

$$\begin{align} \sin^2 \theta_t &= 1 - \cos^2 \theta_t = \eta^2 (1 - \cos^2 \theta_i) \notag \\ \cos^2 \theta_t &= 1 - \eta^2 (1 - \cos^2 \theta_i) \notag \\ \cos \theta_t &= \sqrt{1 - \eta^2 (1 - \cos^2 \theta_i)} \notag \\ T_\perp &= - \cos \theta_t N = - \sqrt{1 - \eta^2 (1 - \cos^2 \theta_i)} N \notag \end{align}$$

最後に，2つのベクトルを加算して屈折ベクトル$T$を得ます．

$$\begin{align} T &= T_\parallel + T_\perp \notag \\ &= \eta (D + \cos \theta_i N) - \cos \theta_t N \notag \\ &= \eta D + (\eta \cos \theta_i - \cos \theta_t) N \notag \end{align}$$

https://github.com/Oya-Tomo/build_your_own_raytracer/blob/main/src/raytracer/raytracer.rs#L318-L358

拡散

拡散には，一般的にはランダムな方向にRayを散らすことで，面が光を均一に反射する様子をシミュレートします．
しかし，今回は簡易的に，法線ベクトルを方向とするRayを生成しています．

再衝突の防止

Rayが面と交差した直後に，その面と再度交差してしまう問題を防止するために，交差点から法線方向に微小なオフセットを加えた位置から新たなRayを発射します．

$$O_{new} = O_{hit} + \epsilon D$$

色の計算

色の話をする前に，光の2分類について説明します．
光には，大きく分けて直接光(direct light)と間接光(indirect light)の2種類があります．
直接光とは，光源から直接物体に届く光のことを指します．
一方，間接光とは，物体から反射・屈折した後に他の物体に届く光のことを指します．

直接光の計算

直接光の計算は，Rayが面と交差した際にその交差点から光源に向けてShadow Rayを発射することで行います．
Shadow Rayが他の物体と交差しなかった場合，その光源からの光が直接交差点に届いていると判定します．

このとき，その光源からの光$L_{emission}$をそのまま加算するのではなく，面の材質・色と照射角度に基づいて減衰させます．
この実装では，素材の色をalbedoで表しています． $C_{albedo}$

$$L_{direct} = C_{albedo} \times L_{emission} \times \max(0, N \cdot D)$$

これをすべての光源に対して計算し，合計したものが直接光の寄与となります．

間接光の計算

間接光の計算は，Rayが面と交差した際に生成された新たなRayを再帰的に追跡することで行います．
最終的には，各Rayに対して，係数をかけて合計することで，間接光の寄与を計算します．

最終的な色の計算

最終的な色$L$は，直接光と間接光の寄与を合計することで計算されます．

$$L = L_{direct} + L_{indirect}$$

ただし，ここで注意なのが，ここで出てくる色の合計値はあくまでRayと面の交点(Rayの終点)における色であり，Rayの始点にその色が届くまでには距離に応じた減衰が発生するという点です．
(e.g. 夕日が赤いのは，長距離を通過する際に青い成分が散乱されてしまうため)

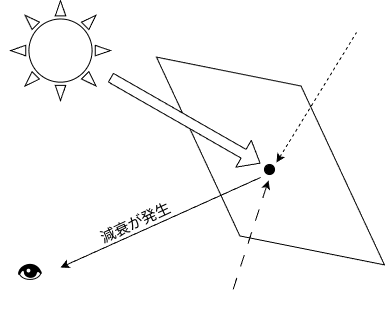
そのため，Rayが通過するマテリアルの吸収係数$C_{absorption}$を用いて，以下のように減衰率$C_{attenuation}$を算出します．

$$C_{attenuation} = \exp(-C_{absorption} \times d)$$

ここで，$d$はRayが通過した距離です．
最終的な色$L$は，以下のように表されます．これで，Rayの始点に届く色が計算できます．

$$L = C_{attenuation} \times (L_{direct} + L_{indirect})$$

簡略化した実装

因みに，普通は物質を金属と非金属に分けるようです．
ざっくり説明すると，金属は光を一度吸収してから反射するため，反射光の色が物質の色に強く影響されます．
一方，非金属は光を吸収せずに反射するため，反射光の色が物質の色にあまり影響されません．

画像への出力

最終的に，各ピクセルに対して計算された色を画像として出力します．
しかしこの実装では，実際の光に基づいて色を計算しているため，色の値が0から1の範囲を超えることがあります．
これを，ハイダイナミックレンジ(HDR)と呼びます．

そのため，最終的な画像に出力する前に，トーンマッピングを行い，色の値を0から1の範囲に収めます．今回は，以下の3つの手法を実装しています．

• Reinhard
• Exposure
• ACES Filmic

Reinhard

Reinhardトーンマッピングは，以下の式で表されます．

$$L_{out} = \frac{L_{in}}{1 + L_{in}}$$

パラメタが無いため，簡単に実装・利用できます．

Exposure

Exposureトーンマッピングは，以下の式で表されます．

$$L_{out} = 1 - \exp(-k \times L_{in})$$

ここで，$k$は露出係数であり，値を大きくするほど明るい画像になります．
係数を調整することで，白飛びや黒つぶれを防ぐことができます．

ACES Filmic

ACES Filmicトーンマッピングは，以下の式で表されます．

$$L_{out} = \frac{L_{in} (A L_{in} + B)}{L_{in} (C L_{in} + D) + E}$$

e.g. $A=2.51, B=0.03, C=2.43, D=0.59, E=0.14$

参考: https://hikita12312.hatenablog.com/entry/2017/08/27/002859

おわりに

今回は，自作した簡易CPUレンダラについて紹介しました．
本当にAI様様で，かなり短時間でここまでRay Tracingの基礎的な仕組みを理解できたことに驚いています．

よく考えてみれば，ゲームエンジンを作っている方たちは，こういった複雑な処理を高速に行えるようにしてくれているだけでなく，更に物理演算までやってくれているわけですから，本当に感謝しかないですね🙏
とりあえず，日々感謝しなががら，シミュレータを使わせていただきます🙇‍♂

今後の展望としては，GPUでの実装や，BVHなどの最適化手法も少しは勉強してみたいと思っています．(いつになるやら...)

以上!!