【LangChain】のRAGの類似度計算の詳細を確認したら色々変だった

はじめに

LangChain で RAG を実装する時、以下のように (FAISS, Chroma などの) 何らかの VectorStore の as_retriever() メソッドで retriever を生成し、invoke() を実行して類似度検索をすると思います。

vectorstore = SomeVectorStore(embeddings)
retriever = vectorstore.as_retriever(search_type="similarity")
result = retriever.invoke("some text")

retriever に指定できる search_type は

1. similarity（類似度検索）
2. similarity_score_threshold（閾値以下切り捨て類似度検索）
3. mmr（極端に似たものを避けて類似度検索）

の 3 つあります。

この中で、similarity_score_threshold の類似度の計算は特殊で、類似度を変換して $0$ ~ $1$ の値にし、かつ $1$ が一番近く、$0$ が一番遠いようにしています。その変換の計算がなんか変です。

この記事ではそれについて説明しますが、変なところが 2 段階になっているのでちょっと読みづらいかもしれません。ご了承ください。

結論をいうと、基本的にそれほど実害はなさそうですが、similarity_score_threshold の動きは結構怪しく、特に FAISS を使う場合は similarity_score_threshold を使わないほうがいいです。FAISS は similarity でも閾値指定できるので、そちらを使ったほうがいいです。

ライブラリのバージョン

動作確認した各ライブラリのバージョンは以下のとおりです。

langchain==0.3.25 langchain_core==0.3.63 langchain_community==0.3.24
langchain-chroma==0.2.4 chromadb==1.0.12 faiss-cpu==1.11.0

ベクトルの類似度計算について

langchain の実装の説明の前に、まず以下の 3 つのベクトルの類似度計算について簡単にまとめます。

• $L^2$ 距離
• コサイン類似度
• 最大内積

この節では一般の $n$ 次元のベクトルを扱いますが、$n = 2$ と思って読んでいただいて問題ありません。

ノルム、内積の定義

$$\begin{align*} a &= (a_1, \cdots, a_n) \\ b &= (b_1, \cdots, b_n) \end{align*}$$

を $n$ 次元ベクトルとします。自然数 $p$ に対して、各成分の $p$ 乗の和の $p$ 乗根

$$||a||_p = \sqrt[p]{a_1^p + \cdots + a_2^p}$$

を $a$ の $L^p$ ノルムと言います。RAG の文脈では基本的に $p = 2$ の場合しか出てこないので

$$|a| = ||a||_2$$

と表すこととします。$|a|$ は次元 $n = 2, 3$ の時は $a$ の普通の意味での長さと一致します。

$n$ 次元ベクトル $a, b$ に対して、各成分の積をとって足し合わせた

$$\langle a, b \rangle = a_1b_1 + \cdots + a_nb_n$$

を $a$ と $b$ の内積と言います。内積については、

$$\begin{gather*} \langle a, a \rangle = |a|^2 \\ \langle a, b \rangle = \langle b, a \rangle \end{gather*}$$

や、3 つの $n$ 次元ベクトル $a, b, c$ に対して

$$\langle a + c, b \rangle = \langle a, b \rangle + \langle c, b \rangle$$

が成り立ちます。

$L^2$ 距離

$L^2$ 距離は $a$ と $b$ の離れ具合を $a-b$ の長さ $|a-b|$ で測ります。$|a-b|$ が小さいほど $a$ と $b$ は近いと判断します。$L^2$ 距離はユークリッド距離と呼ばれることもあります。計算すると

$$\begin{align*} |a-b|^2 &= \langle a-b, a-b \rangle \\ &= \langle a, a\rangle -2 \langle a, b \rangle + \langle b, b\rangle \\ &= |a|^2 + |b|^2 -2 \langle a, b \rangle \end{align*}$$

となります。また余弦定理から、$a$ と $b$ のなす角を $\theta$ とおくと

$$\langle a, b \rangle = |a| \cdot |b| \cos \theta$$

が成り立ちます。よって

$$\begin{align*} |a-b| &= \sqrt{|a|^2 + |b|^2 -2 \langle a, b \rangle}\\ &= \sqrt{|a|^2 + |b|^2 -2 |a|\cdot|b| \cos \theta}\\ \end{align*}$$

と計算することができます。特に $|a| = |b|=1$ ならば

$$|a-b| = \sqrt{2 -2\cos \theta}$$

となり、$-1 \leq \cos \theta \leq 1$ なので $0 \leq |a-b| \leq 2$ となります。

$|a-b|^2$ の方が平方根を取る必要がなく計算コストが少ないので、こちらを使う場合もあります。

cos 類似度

cos 類似度は、ベクトルの近さを 2 つのベクトルのなす角のみで測る方法で、その角度が小さいほど似ていると判断します。

ベクトル $a$, $b$ のなす角を $\theta$ とします。このとき $0^{\circ} \leq \theta \leq 180^{\circ}$ で、$\cos \theta$ は $\theta = 0$ のとき最大値 $1$ をとり、$\theta$ が大きくなるほど $\cos \theta$ の値は小さくなり、$\theta = 180^{\circ}$ で最小値 $-1$ を取ります。

よって $\cos \theta$ が大きいほど 2 つのベクトルは近く、小さいほど 2 つのベクトルは遠いといえます。

$|a| = |b|=1$ であれば、先ほど求めたように $L^2$ 距離 $|a -b|$ は $\cos \theta$ のみで表すことができるので、どちらを用いても実質同じです。

最大内積

最大内積は内積が大きいほど近いと考えます。余弦定理から

$$\langle a, b \rangle = |a|\cdot|b| \cos \theta$$

なので、$|a| = |b|=1$ であれば cos 類似度と同じです。内積を計算するだけなので他の類似度よりも計算が楽です。

LangChain の類似度計算

まず簡単に LangChain の類似度計算の処理流れについて説明し、その後 Chroma と FAISS の動作確認をします。

処理の流れ

冒頭で述べたように、埋め込みベクトルによる類似度計算を行う時は

vectorstore = SomeVectorStore(embeddings)
retriever = vectorstore.as_retriever(search_type="similarity")
result = retriever.invoke("some text")

のように書きます。invoke() の中身では _get_relevant_documents() というメソッドを実行しており、その中で search_type によって vectorstore の類似度検索方法を変えています。

_get_relevant_documents の中身

https://github.com/langchain-ai/langchain/blob/master/libs/core/langchain_core/vectorstores/base.py#L1073-L1092

search_type	呼ばれるメソッド	説明
similarity	self.vectorstore.similarity_search()	スコアを元に検索する
similarity_score_threshold	self.vectorstore.similarity_search_with_relevance_scores()	関連度を元に検索する
mmr	self.vectorstore.max_marginal_relevance_search()	省略

mmr はこの記事では考えないこととします。

ここでスコアとは、$L^2$ 距離や cos 類似度のことを指すこととします。関連度 (relevance score) は、大きいほど近いようにスコアを変換したものです ($L^2$ 距離は小さいほど近い、cos類似度は大きいほど近い)。本当は 0 ~ 1 になるように正規化することを想定しているようですが、ほとんどの場合そうなっていません。

真ん中の similarity_search_with_relevance_scores() に必要な、関連度の計算についてもう少し深掘りしましょう。

関連度の計算について

関連度への変換については VectorStore というベースクラスに、スコアの算出方法毎に関数が用意されています。用意されているものの、(長さを 1 に正規化しているかどうかなど) 個々の事情で計算方法が異なるため、オーバーライドする想定のようですが、FAISS と Chroma ではそのまま使われています。

L2距離の関連度計算の関数

https://github.com/langchain-ai/langchain/blob/master/libs/core/langchain_core/vectorstores/base.py#L406-L432

cos類似度の関連度計算の関数

https://github.com/langchain-ai/langchain/blob/master/libs/core/langchain_core/vectorstores/base.py#L421-L424

最大内積の関連度計算の関数

https://github.com/langchain-ai/langchain/blob/master/libs/core/langchain_core/vectorstores/base.py#L426-L432

実はこれらの関数のすべて、処理がおかしいです。一つひとつ確認していきましょう。

$L^2$ 距離の関連度計算

まずは $L^2$ 距離の場合の関連度計算について見ていきましょう。

L2距離の関連度計算の関数

https://github.com/langchain-ai/langchain/blob/master/libs/core/langchain_core/vectorstores/base.py#L406-L432

$L^2$ 距離の値 $d$ に対して以下の式で関連度を計算しています。

$$f_{L^2}(d) = 1 -\frac{d}{\sqrt{2}}$$

そして関数のコメントに

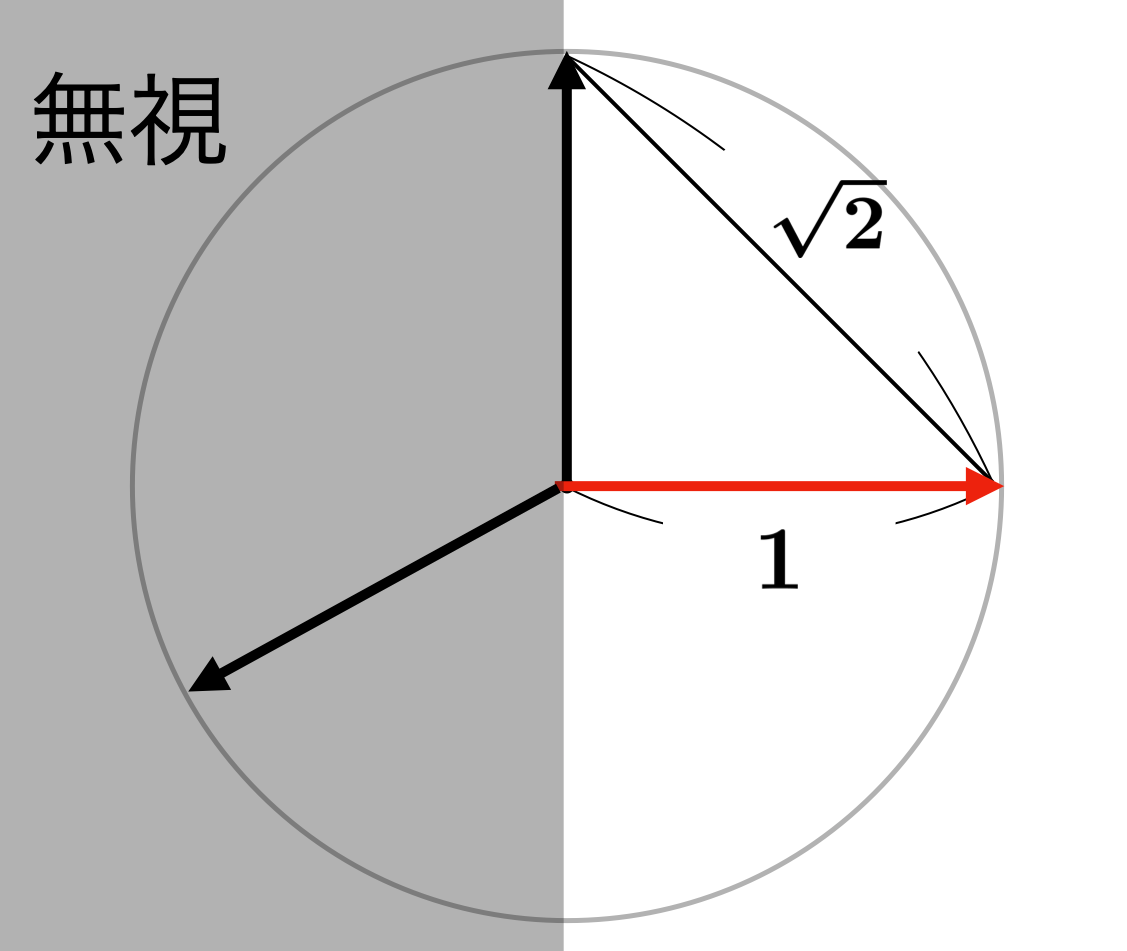
# This function converts the Euclidean norm of normalized embeddings
# (0 is most similar, sqrt(2) most dissimilar)
# to a similarity function (0 to 1)

と、"ベクトルの長さが $1$ に正規化された (normalized embeddings) 場合の $L^2$ 距離 (Euclidiean norm) は $0$ が最も近く、$\sqrt{2}$ が最も遠い" と書いてありますが、$L^2$ 距離の最大値は $2$ です。なので関連度の値は $0$ 以下になる場合があります。

一応以下のように、角度が $90^{\circ}$ 以上のものは無視することにすれば上の計算は正当化できます。実運用上、そんなに離れたベクトルは無視して良いので、実害はないと思われます。

cos 類似度の関連度計算

次は cos 類似度の関連度計算について見ていきましょう。

cos類似度の関連度計算の関数

https://github.com/langchain-ai/langchain/blob/master/libs/core/langchain_core/vectorstores/base.py#L421-L424

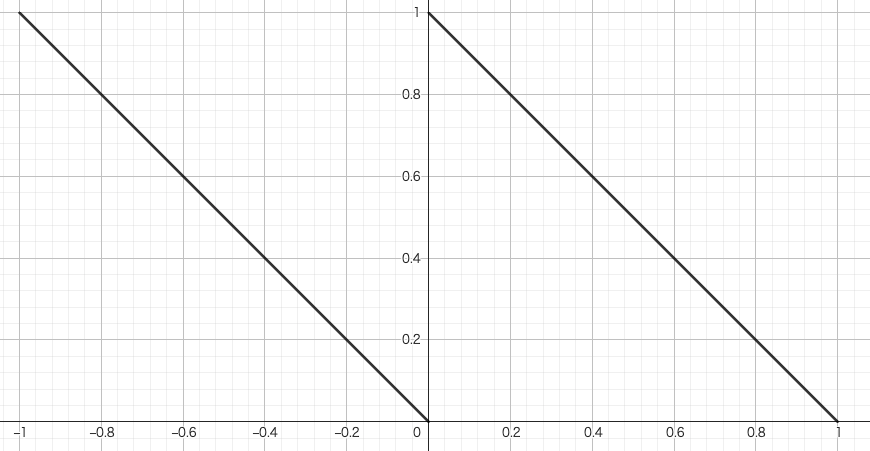
式で表すと

$$f_{\cos}(d) = 1 -d$$

となっています。引数の名前が distance なので、$d = 1 -\cos \theta$ ( $-1 \leq \cos\theta \leq 1$ なので $0 \leq d \leq 2$ ) を想定している可能性が高く、もしそうであれば

$$f_{\cos}(d) = 1 -(1 -\cos \theta)= \cos \theta$$

となります。しかし $0 \leq f_{\cos}(d) \leq 1$ という条件を満たさないという問題があります。さっきと同様に $90^{\circ} < \theta$ を無視すれば、2 番目の問題は解消されます。

最大内積の関連度

最後に最大内積の関連度計算について見ていきましょう。

最大内積の関連度計算の関数

https://github.com/langchain-ai/langchain/blob/master/libs/core/langchain_core/vectorstores/base.py#L426-L432

式で表すと

$$f_{mip}(d) = \begin{cases}1 -d & (d > 0) \\ -d & (d \leq 0)\end{cases}$$

となります。ベクトルの長さが $1$ に正規化されているならば、余弦定理から内積の値は $\cos \theta$ と一致するので、$d > 0$ のときは cos 類似度と同じです。しかし $d \leq 0$ のでは異なります。これをどのように解釈すべきか全くわかりません ( distance なのになぜマイナスなのか) が、

$f_{mip}$のグラフ

動作確認

ここからは実際に動かして、類似度計算がどのように行われているか確認します。詳細は以下の Colaboratory に残しています。

https://colab.research.google.com/drive/1Y7fPFsYUxuk3eDpjZPqghYP5_TJR2qFs

準備

OpenAI 等のちゃんとした Embedding を使うと動作確認がしづらいので、以下のようなダミーの埋め込みを定義します。

from langchain_core.embeddings import Embeddings

class DummyEmbeddings(Embeddings):
    def embed_documents(self, texts: list[str]) -> list[list[float]]:
        return [self.embed_query(text) for text in texts]

    def embed_query(self, text: str) -> list[float]:
        if text == "こんにちは":
            return [1, 0]
        elif text == "おはよう":
            return [-1, 0]
        else:
            return [0, 1]

Chroma の動作

Chroma の cos 類似度と $L^2$ 距離の動作確認をします。ただし、Retriever はテキスト入力しか受け付けず、スコアも返さないので動作確認には向いていません。よって vectorstore の関数を直接実行します。

cos 類似度の動作確認

db = Chroma.from_texts(
    ["こんにちは", "おはよう", "こんばんは"],
    embedding=DummyEmbeddings(),
    persist_directory="cos",
    collection_metadata={"hnsw:space": "cosine"}
)

search_type="similarity" の場合、$1 -\cos\theta$ をスコアとしているようです。

db.similarity_search_with_score("こんにちは")
# 結果
# こんにちは 0.0
# こんばんは 1.0
# おはよう 2.0

search_type="similarity_score_threshold" の場合、$\cos \theta$ を関連度としているようです。

db.similarity_search_with_relevance_scores("こんにちは")
# 結果
# こんにちは 1.0
# こんばんは 0.0
# おはよう -1.0

閾値を指定すると以下のようになります。

# 閾値 0
db.as_retriever(
    search_type="similarity_score_threshold",
    search_kwargs={"score_threshold": 0.0, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは
# こんばんは

# 閾値 0.2
db.as_retriever(
    search_type="similarity_score_threshold",
    search_kwargs={"score_threshold": 0.2, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは

よって $\cos \theta$ の値で閾値を判断しているようです。

$L^2$ 距離の動作確認

db_l2 = Chroma.from_texts(
    ["こんにちは", "おはよう", "こんばんは"],
    embedding=DummyEmbeddings(),
    persist_directory="l2",
    collection_metadata={"hnsw:space": "l2"}
)

search_type="similarity" の場合、$|a -b|^2$ を関連度としているようです。

db_l2.similarity_search_with_score("こんにちは")
# 結果
# こんにちは 0.0
# こんばんは 2.0
# おはよう 4.0

search_type="similarity_score_threshold" の場合、$1 -\frac{|a -b|^2}{\sqrt{2}}$ を関連度としているようです。

db_l2.similarity_search_with_relevance_scores("こんにちは")
# 結果
# こんにちは 1.0
# こんばんは -0.4142135623730949
# おはよう -1.8284271247461898

閾値を指定すると以下のようになります。

# 閾値指定 -0.3
db_l2.as_retriever(
    search_type="similarity_score_threshold",
    search_kwargs={"score_threshold": -0.3, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは

# 閾値指定 -0.5
db_l2.as_retriever(
    search_type="similarity_score_threshold",
    search_kwargs={"score_threshold": -0.5, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは
# こんばんは

閾値は $1 -\frac{|a -b|^2}{\sqrt{2}}$ で判定しているようです。

FAISS の動作

FAISS の cos 類似度と $L^2$ 距離の動作確認をしますが、FAISS で cos 類似度を用いる場合は、DistanceStrategy を MAX_INNER_PRODUCT にしないと Index が想定通りに生成されないようなので、最大内積を指定します。

https://qiita.com/shimajiroxyz/items/705aca029ba1bc395df6

cos 類似度の動作確認

faiss = FAISS.from_texts(
    ["こんにちは", "おはよう", "こんばんは"],
    embedding=DummyEmbeddings(),
    normalize_L2=True,
    distance_strategy=DistanceStrategy.MAX_INNER_PRODUCT
)

search_type="similarity" の場合、スコアは $\cos \theta$ で計算されます。これは Chroma が $1 -\cos\theta$ だったのと異なります。

faiss.similarity_search_with_score("こんにちは")
# 結果
# こんにちは 1.0
# こんばんは 0.0
# おはよう -1.0

search_type="similarity_score_threshold" の場合、関連度は以下のようになります (めちゃくちゃです)。

faiss.similarity_search_with_relevance_scores("こんにちは")
# 結果
# こんにちは 0.0
# こんばんは -0.0
# おはよう 1.0
# 1 - cosθ if cosθ > 0 else -cosθ (謎実装)

閾値を指定すると以下のようになります。関連度の計算が変であることに加えて、切り捨てるべき方向が逆なので、なぜか一番遠いはずの "おはよう" だけが残ります。

faiss.as_retriever(
    search_type="similarity_score_threshold",
    search_kwargs={"score_threshold": 0.1, "k": 6}
).invoke("こんにちは")
# 結果
# おはよう

FAISS は実は、search_type="similarity" でも閾値指定でき、そっちを使ったほうが良いです。

faiss.as_retriever(
    search_type="similarity",
    search_kwargs={"score_threshold": 0.1, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは

faiss.as_retriever(
    search_type="similarity",
    search_kwargs={"score_threshold": -0.1, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは
# こんばんは

$L^2$ 距離の動作確認

faiss_l2 = FAISS.from_texts(
    ["こんにちは", "おはよう", "こんばんは"],
    embedding=DummyEmbeddings(),
    normalize_L2=True,
    distance_strategy=DistanceStrategy.EUCLIDEAN_DISTANCE
)

search_type="similarity" の場合は、$|a -b|^2$ をスコアとしているようです。

faiss_l2.similarity_search_with_score("こんにちは")
# 結果
# こんにちは 0.0
# こんばんは 2.0
# おはよう 4.0

search_type="similarity_score_threshold" の場合、$1 -\frac{|a -b|^2}{\sqrt{2}}$ を関連度としているようです。

faiss_l2.similarity_search_with_relevance_scores("こんにちは")
# 結果
# こんにちは 1.0
# こんばんは -0.41421354
# おはよう -1.8284271

閾値を指定すると以下のようになります。指定した閾値より関連度が小さいものが切り捨てられます。

# 閾値 -0.1
faiss_l2.as_retriever(
    search_type="similarity_score_threshold",
    search_kwargs={"score_threshold": -0.1, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは

# 閾値 -0.5
faiss_l2.as_retriever(
    search_type="similarity_score_threshold",
    search_kwargs={"score_threshold": -0.5, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは
# こんばんは

ここまでは Chroma の $L^2$ 同じ動作をします。

最後に一応、search_type="similarity" の場合の閾値指定について確認します。$|a -b|^2$ の値で足切りされます。

# 閾値 0.1
faiss_l2.as_retriever(
    search_type="similarity",
    search_kwargs={"score_threshold": 0.1, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは

# 閾値 1.1
faiss_l2.as_retriever(
    search_type="similarity",
    search_kwargs={"score_threshold": 1.1, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは

# 閾値 2.1
faiss_l2.as_retriever(
    search_type="similarity",
    search_kwargs={"score_threshold": 2.1, "k": 6}
).invoke("こんにちは")
# 結果
# こんにちは
# こんばんは

結論

• FAISS で閾値を指定したい場合、search_type="similarity_score_threshold" ではなく search_type="similarity" を使ったほうが良い。
• スコア、関連度の算出がベクターストアによって異なる可能性があるので確認したほうが良い。
• Retriever がスコアを返してくれないせいで問題が見つかりにくい。