HaskellでStateパターンを実装する (Haskell初心者が電卓アプリを作る 3)
この記事について
この記事は連載記事「Haskell初心者が電卓アプリを作る」の3回目の記事です。
本記事では、Haskell での State パターンの実装について記載します。
-
Haskellでstateパターンを実装する (Haskell初心者が電卓アプリを作る 3) ← 今ここ
ソースコードは以下にアップしています。
https://github.com/daikon-oroshi/haskell-calculator-sample
State パターンに State モナドを使わなかった
実装前は State パターンと State モナドには深い関係があると思っていたのですが、今回の実装では State モナドを使いませんでした。また、実装してみて、少なくともコーディングする上ではこの二つはあまり関係ないと感じました。その理由を述べる前に、モナドと State モナドについて軽く説明します。
モナドとは
モナドを知らない方は、モナドとは「合成できる仕組み」の事だと思ってください。ここでの合成は関数の合成
少し凝った例だと、例えば
と定義すると
プログラムでは
副作用以外にも、モナドを用いて表現できる合成があります。
モナドの定義のおさらい
モナドの定義について軽くおさらいすると、モナド
が存在するものでした (本当はもう少し条件があります)。
例えば List モナドは任意の型
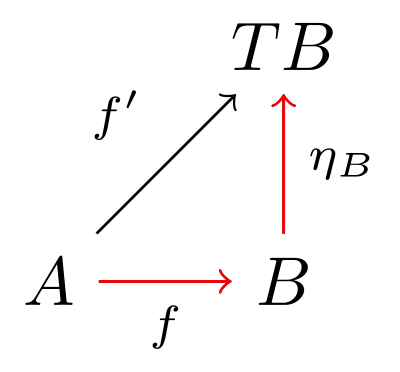
また、
このとき、
また、普通の関数
State モナドとは
型
と定義されます。右辺の
は
をカリー化したもの、つまり
で与えられ、
は
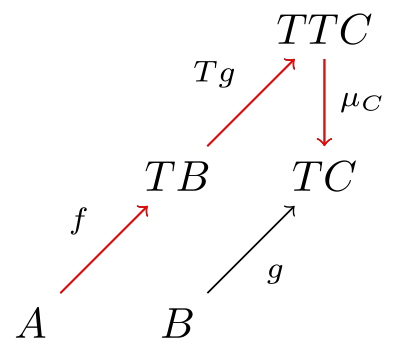
で与えられます。ここで
合成を考えましょう。
はアンカリー化すると
であり、
のカリー化と一致します。つまり、型
要素を用いて表すと
となります。
State モナドを使わなかった理由 1
電卓アプリではボタン操作の度に現在の状態を更新する必要があります。State モナドは状態を保持するのではなく、状態を渡していくだけなので、実行するたびに初期値から計算されてしまい、意図した動作になりません。
状態を保持するには STRef (STモナド) を使う方法と IORef を使う方法があります。IORef を使うのなんでもできそうなのでなるべく使いたくなかったのですが、click のコールバック関数の型が IO() だったので IORef を使いました。
理由はもう一つありますが、実装上の問題なので後ほど述べます。
State パターンの実装
まず各 step の型を
data FirstInputStep = FirstInputStep
data OperationSelectedStep = OperationSelectedStep
data SecondInputStep = SecondInputStep
data ResultStep = ResultStep
data CalcStep = forall s. (ICalcStep s) => CalcStep s
と定義して、
data CalcState v = (CalcValue v) => CalcState {
csStep :: CalcStep,
csCurrentVal :: v,
csPrevVal :: v,
csOperation :: Maybe Operation
}
とします。つまり現在の状態を step と入力した値 (第 1 変数と第 2 変数) と演算の組を値として表します。step を持っているのはあまり良くないですが、今は気にしないことにします。
step のインターフェイスを
class ICalcStep a where
actionDigit :: (CalcValue v) => a -> CalcState v -> Int -> CalcState v
actionDot :: (CalcValue v) => a -> CalcState v -> CalcState v
actionZeroZero :: (CalcValue v) => a -> CalcState v -> CalcState v
actionPm :: (CalcValue v) => a -> CalcState v -> CalcState v
actionAc :: (CalcValue v) => a -> CalcState v -> CalcState v
actionC :: (CalcValue v) => a -> CalcState v -> CalcState v
actionOperation :: (CalcValue v) => a -> CalcState v -> Operation -> CalcState v
actionEq :: (CalcValue v) => a -> CalcState v -> CalcState v
と定義して、各キーの操作を実行するメソッドを持つようにします。
第1引数を無視すれば、それぞれ CalcState (+ α)を受け取って CalcState を返す関数であり、step を遷移する場合は csStep を変更することで状態遷移を実装します。
instance ICalcStep FirstInputStep where
actionOperation :: FirstInputStep -> CalcState v -> Operation -> CalcState v
actionOperation _ st op =
st {
csStep = CalcStep OperationSelectedStep,
csOperation = Just op
}
...
問題点と改善点
この実装で state パターンは実現できていますが、いくつか問題があります。
-
step を値として持っているのは気持ち悪い。型として定義すべき。
-
ファイルを step 毎に分割できない (循環 import 問題)。
-
冗長なところがある。特に CalcStep を ICalcStep のインスタンスにするところ。
これらは data family というものを使うと解決できるようです。
State モナドを使わなかった理由 2
ICalcStep クラスのそれぞれのメソッドは CalcState (+ α) を受け取って CalcState を返す関数なので、State モナドを使うことができます。ですが、それぞれのメソッドは別個に呼び出されるため、引数を順次渡していく仕組みである State モナドを使うメリットがありません。
まとめ
Haskell でアプリを実装してみて、思っていたよりクセがないという印象です。ポリモーフィズムが手軽に実装できますし、関数の引数のパターンマッチのお陰で if 文が少なくて済みます。仮に実装に困っても IORef をつかえば大体なんとかできそうです。
一方で、関数名の被りに厳しいところが面倒に感じました。他言語であれば、あるクラスに足し算を定義したいときに + 演算だけ定義することができますが、Haskell では + は Num クラスの + と被るため、+ を定義しようとすると、Num クラスのインスタンスにするために掛け算、abs等、他のメソッドを定義する必要があります。
また、ライブラリを使うと知らない演算子が現れたり、コンパイルエラーの内容が分かりづらかったり、役に立つサンプルコードが少なかったりと結構ハードルが高かったです。
Discussion