Closed9
コンピュータシステムの理論と実装 & 回路遊び
これをやってく。
1章 ブール論理
- PCは電気信号のon,offで動くので、2進法を学ぶ必要がある
- ブール代数(2進法の学問)
- ブール値
- 2つのラベルを持った値
- ブール関数
- ブール地を引数に持つ関数
- And,Or,Notが演算の構成要素(10進法でいう四則演算)
- 真理値表やブール式(+,・のような演算子を用いた表現)で表すことができる
- ブール式では↓のようになる
- And(X,Y)=x・y
- Or(X,Y)=x+y
- Not(X)=X¯
- 正規表現
- 複数のブール値を一つのブール式にまとめたもの
- 要素数がnこの場合、正規表は4^n通りある
- 任意のブール関数は少なくとも一つの正規表現で表すことができる
- 任意のブール関数は、・(And)、+(Or)、¯(Not)で表せる
- ・(And)、+(Or)、¯(Not)は、Nandから作ることができるので、任意のブール関数はNandで表現できる
- Nand
- Not andの略
- NandでAnd,Or,Notを表現できる
- 論理ゲート
- ブール関数を物理的に実現したデバイス
- And,Or,Noに対する論理ゲートを基本論理ゲートという
- 複数の基本論理ゲートを組み合わせてできるものを複合ゲートという
Not.hdl
Not.hdl
CHIP Not {
IN in;
OUT out;
PARTS:
Nand(a=in, b=in, out=out);
}
And.hdl
And.hdl
CHIP And {
IN a, b;
OUT out;
PARTS:
Nand(a=a, b=b, out=out1);
Nand(a=out1, b=out1, out=out);
}
Or.hdl
Or.hdl
CHIP Or {
IN a, b;
OUT out;
PARTS:
Nand(a=a, b=a, out=out1);
Nand(a=b, b=b, out=out2);
Nand(a=out1, b=out2, out=out);
}
Not16.hdl
Not16.hdl
CHIP Not16 {
IN in[16];
OUT out[16];
PARTS:
Nand(a=in[0],b=in[0],out=out[0]);
Nand(a=in[1],b=in[1],out=out[1]);
Nand(a=in[2],b=in[2],out=out[2]);
Nand(a=in[3],b=in[3],out=out[3]);
Nand(a=in[4],b=in[4],out=out[4]);
Nand(a=in[5],b=in[5],out=out[5]);
Nand(a=in[6],b=in[6],out=out[6]);
Nand(a=in[7],b=in[7],out=out[7]);
Nand(a=in[8],b=in[8],out=out[8]);
Nand(a=in[9],b=in[9],out=out[9]);
Nand(a=in[10],b=in[10],out=out[10]);
Nand(a=in[11],b=in[11],out=out[11]);
Nand(a=in[12],b=in[12],out=out[12]);
Nand(a=in[13],b=in[13],out=out[13]);
Nand(a=in[14],b=in[14],out=out[14]);
Nand(a=in[15],b=in[15],out=out[15]);
}
And16.hdl
And16.hdl
CHIP And16 {
IN a[16], b[16];
OUT out[16];
PARTS:
Nand(a=a[0], b=b[0], out=out0);
Nand(a=out0, b=out0, out=out[0]);
Nand(a=a[1], b=b[1], out=out1);
Nand(a=out1, b=out1, out=out[1]);
Nand(a=a[2], b=b[2], out=out2);
Nand(a=out2, b=out2, out=out[2]);
Nand(a=a[3], b=b[3], out=out3);
Nand(a=out3, b=out3, out=out[3]);
Nand(a=a[4], b=b[4], out=out4);
Nand(a=out4, b=out4, out=out[4]);
Nand(a=a[5], b=b[5], out=out5);
Nand(a=out5, b=out5, out=out[5]);
Nand(a=a[6], b=b[6], out=out6);
Nand(a=out6, b=out6, out=out[6]);
Nand(a=a[7], b=b[7], out=out7);
Nand(a=out7, b=out7, out=out[7]);
Nand(a=a[8], b=b[8], out=out8);
Nand(a=out8, b=out8, out=out[8]);
Nand(a=a[9], b=b[9], out=out9);
Nand(a=out9, b=out9, out=out[9]);
Nand(a=a[10], b=b[10], out=out10);
Nand(a=out10, b=out10, out=out[10]);
Nand(a=a[11], b=b[11], out=out11);
Nand(a=out11, b=out11, out=out[11]);
Nand(a=a[12], b=b[12], out=out12);
Nand(a=out12, b=out12, out=out[12]);
Nand(a=a[13], b=b[13], out=out13);
Nand(a=out13, b=out13, out=out[13]);
Nand(a=a[14], b=b[14], out=out14);
Nand(a=out14, b=out14, out=out[14]);
Nand(a=a[15], b=b[15], out=out15);
Nand(a=out15, b=out15, out=out[15]);
}
Or16.hdl
Or16.hdl
CHIP Or16 {
IN a[16], b[16];
OUT out[16];
PARTS:
Nand(a=a[0], b=a[0], out=outa0);
Nand(a=b[0], b=b[0], out=outb0);
Nand(a=outa0, b=outb0, out=out[0]);
Nand(a=a[1], b=a[1], out=outa1);
Nand(a=b[1], b=b[1], out=outb1);
Nand(a=outa1, b=outb1, out=out[1]);
Nand(a=a[2], b=a[2], out=outa2);
Nand(a=b[2], b=b[2], out=outb2);
Nand(a=outa2, b=outb2, out=out[2]);
Nand(a=a[3], b=a[3], out=outa3);
Nand(a=b[3], b=b[3], out=outb3);
Nand(a=outa3, b=outb3, out=out[3]);
Nand(a=a[4], b=a[4], out=outa4);
Nand(a=b[4], b=b[4], out=outb4);
Nand(a=outa4, b=outb4, out=out[4]);
Nand(a=a[5], b=a[5], out=outa5);
Nand(a=b[5], b=b[5], out=outb5);
Nand(a=outa5, b=outb5, out=out[5]);
Nand(a=a[6], b=a[6], out=outa6);
Nand(a=b[6], b=b[6], out=outb6);
Nand(a=outa6, b=outb6, out=out[6]);
Nand(a=a[7], b=a[7], out=outa7);
Nand(a=b[7], b=b[7], out=outb7);
Nand(a=outa7, b=outb7, out=out[7]);
Nand(a=a[8], b=a[8], out=outa8);
Nand(a=b[8], b=b[8], out=outb8);
Nand(a=outa8, b=outb8, out=out[8]);
Nand(a=a[9], b=a[9], out=outa9);
Nand(a=b[9], b=b[9], out=outb9);
Nand(a=outa9, b=outb9, out=out[9]);
Nand(a=a[10], b=a[10], out=outa10);
Nand(a=b[10], b=b[10], out=outb10);
Nand(a=outa10, b=outb10, out=out[10]);
Nand(a=a[11], b=a[11], out=outa11);
Nand(a=b[11], b=b[11], out=outb11);
Nand(a=outa11, b=outb11, out=out[11]);
Nand(a=a[12], b=a[12], out=outa12);
Nand(a=b[12], b=b[12], out=outb12);
Nand(a=outa12, b=outb12, out=out[12]);
Nand(a=a[13], b=a[13], out=outa13);
Nand(a=b[13], b=b[13], out=outb13);
Nand(a=outa13, b=outb13, out=out[13]);
Nand(a=a[14], b=a[14], out=outa14);
Nand(a=b[14], b=b[14], out=outb14);
Nand(a=outa14, b=outb14, out=out[14]);
Nand(a=a[15], b=a[15], out=outa15);
Nand(a=b[15], b=b[15], out=outb15);
Nand(a=outa15, b=outb15, out=out[15]);
}
Or8Way.hdl
Or8Way.hdl
CHIP Or8Way {
IN in[8];
OUT out;
PARTS:
Nand(a=in[0], b=in[0], out=outa0);
Nand(a=in[1], b=in[1], out=outb0);
Nand(a=outa0, b=outb0, out=out0);
Nand(a=out0, b=out0, out=outa1);
Nand(a=in[2], b=in[2], out=outb1);
Nand(a=outa1, b=outb1, out=out1);
Nand(a=out1, b=out1, out=outa2);
Nand(a=in[3], b=in[3], out=outb2);
Nand(a=outa2, b=outb2, out=out2);
Nand(a=out2, b=out2, out=outa3);
Nand(a=in[4], b=in[4], out=outb3);
Nand(a=outa3, b=outb3, out=out3);
Nand(a=out3, b=out3, out=outa4);
Nand(a=in[5], b=in[5], out=outb4);
Nand(a=outa4, b=outb4, out=out4);
Nand(a=out4, b=out4, out=outa5);
Nand(a=in[6], b=in[6], out=outb5);
Nand(a=outa5, b=outb5, out=out5);
Nand(a=out5, b=out5, out=outa6);
Nand(a=in[7], b=in[7], out=outb6);
Nand(a=outa6, b=outb6, out=out);
}
Xor.hdl
Xor.hdl
CHIP Xor {
IN a, b;
OUT out;
PARTS:
Not(in=a, out=outNota);
Not(in=b, out=outNotb);
And(a=a,b=outNotb,out=out1);
And(a=outNota,b=b,out=out2);
Or(a=out1,b=out2,out=out);
}
Mux_take1.hdl
Mux_take1.hdl
CHIP Mux {
IN a, b, sel;
OUT out;
PARTS:
Not(in=a,out=notA);
Not(in=b,out=notB);
Not(in=sel,out=notSel);
And(a=a,b=b,out=outAB);
And(a=a,b=notB,out=outANotB);
And(a=notA,b=b,out=outNotAB);
And(a=outANotB,b=notSel,out=outANotBNotSel);
And(a=outAB,b=notSel,out=outABNotSel);
And(a=outNotAB,b=sel,out=outNotABSel);
And(a=outAB,b=sel,out=outABSel);
Or(a=outANotBNotSel,b=outABNotSel,out=outANotBNotSelAndABNotSel);
Or(a=outNotABSel,b=outABSel,out=outNotABSelAndABSel);
Or(a=outANotBNotSelAndABNotSel,b=outNotABSelAndABSel,out=out);
}
Mux_take2.hdl
Mux_take2.hdl
Mux4Way16.hdl
Mux4Way16.hdl
CHIP Mux4Way16 {
IN a[16], b[16], c[16], d[16], sel[2];
OUT out[16];
PARTS:
Mux16(a=a,b=b,sel=sel[0],out=outab);
Mux16(a=c,b=d,sel=sel[0],out=outcd);
Mux16(a=outab,b=outcd,sel=sel[1],out=out);
}
Mux8Way16.hdl
Mux8Way16.hdl
CHIP Mux8Way16 {
IN a[16], b[16], c[16], d[16],
e[16], f[16], g[16], h[16],
sel[3];
OUT out[16];
PARTS:
Mux4Way16(a=a,b=b,c=c,d=d,sel=sel[0..1],out=outabcd);
Mux4Way16(a=e,b=f,c=g,d=h,sel=sel[0..1],out=outefgh);
Mux16(a=outabcd,b=outefgh,sel=sel[2],out=out);
}
DMux.hdl
DMux.hdl
CHIP DMux {
IN in, sel;
OUT a, b;
PARTS:
Not(in=sel,out=notSel);
And(a=in,b=notSel,out=a);
And(a=in,b=sel,out=b);
}
DMux4Way.hdl
DMux4Way.hdl
CHIP DMux4Way {
IN in, sel[2];
OUT a, b, c, d;
PARTS:
DMux(in=in, sel=sel[1], a=w1, b=w2);
DMux(in=w1, sel=sel[0], a=a, b=b);
DMux(in=w2, sel=sel[0], a=c, b=d);
}
DMux8Way.hdl
DMux8Way.hdl
CHIP DMux8Way {
IN in, sel[3];
OUT a, b, c, d, e, f, g, h;
PARTS:
DMux4Way(in=in, sel=sel[1..2], a=w1, b=w2, c=w3, d=w4);
DMux(in=w1, sel=sel[0], a=a, b=b);
DMux(in=w2, sel=sel[0], a=c, b=d);
DMux(in=w3, sel=sel[0], a=e, b=f);
DMux(in=w4, sel=sel[0], a=g, b=h);
}
2章 ブール算術
- 2進数加算
- 10進数と同じく、各桁で足し合わせ、1を超えたら桁上げ(キャリー)が発生する
- 算術オーバフロー
- コンピュータで扱える桁数(ビット数)の上限を超えたしまった状態
- オーバーフローが起きた時の処理は、エラー出力してプログラム停止、オーバーフローで溢れたビットを無視など、色々シナリオがある
- 2の補数で、2進数の負の数を表現できる
- 以下で計算できる
- 各ビットの数を反転させる
- 最下位ビットに1を加える
- 元の数と補数を足すと0になる(算術オーバフローは無視される)
- 正の数の最上位ビットは0
- 負の数の最上位ビットは1
- 以下で計算できる
- 符号付き2進数では、最上位ビットが1の場合は負の数として扱うこと注意!!!
- 符号を考慮していない時みたいに単純にシグマで計算できない
- 2の補数を使うと減算は加算として扱えるので複雑性が減る
- 加算器
- 半加算器
- 全加算器
- 多ビット半加算器
- インクリメンタ
- ALU(Arithmetic and Logic Unit)
- 算術論理演算機
- 算術演算、論理演算を処理する装置
- 制御ビットによって演算の内容が操作される
- ALU一つで、AND,ORやらの回路を処理できる
HalfAdder.hdl
HalfAdder.hdl
CHIP HalfAdder {
IN a, b; // 1-bit inputs
OUT sum, // Right bit of a + b
carry; // Left bit of a + b
PARTS:
And(a=a,b=b,out=carry);
Xor(a=a,b=b,out=sum);
}
FullAdder.hdl
FullAdder.hdl
CHIP FullAdder {
IN a, b, c; // 1-bit inputs
OUT sum, // Right bit of a + b + c
carry; // Left bit of a + b + c
PARTS:
HalfAdder(a=a,b=b,sum=sum0,carry=carry0);
HalfAdder(a=sum0,b=c,sum=sum,carry=carry1);
Or(a=carry0,b=carry1,out=carry);
}
Add16.hdl
Add16.hdl
CHIP Add16 {
IN a[16], b[16];
OUT out[16];
PARTS:
HalfAdder(a=a[0], b=b[0], sum=out[0], carry=carry0);
FullAdder(a=a[1], b=b[1], c=carry0, sum=out[1], carry=carry1);
FullAdder(a=a[2], b=b[2], c=carry1, sum=out[2], carry=carry2);
FullAdder(a=a[3], b=b[3], c=carry2, sum=out[3], carry=carry3);
FullAdder(a=a[4], b=b[4], c=carry3, sum=out[4], carry=carry4);
FullAdder(a=a[5], b=b[5], c=carry4, sum=out[5], carry=carry5);
FullAdder(a=a[6], b=b[6], c=carry5, sum=out[6], carry=carry6);
FullAdder(a=a[7], b=b[7], c=carry6, sum=out[7], carry=carry7);
FullAdder(a=a[8], b=b[8], c=carry7, sum=out[8], carry=carry8);
FullAdder(a=a[9], b=b[9], c=carry8, sum=out[9], carry=carry9);
FullAdder(a=a[10], b=b[10], c=carry9, sum=out[10], carry=carry10);
FullAdder(a=a[11], b=b[11], c=carry10, sum=out[11], carry=carry11);
FullAdder(a=a[12], b=b[12], c=carry11, sum=out[12], carry=carry12);
FullAdder(a=a[13], b=b[13], c=carry12, sum=out[13], carry=carry13);
FullAdder(a=a[14], b=b[14], c=carry13, sum=out[14], carry=carry14);
FullAdder(a=a[15], b=b[15], c=carry14, sum=out[15], carry=carry);
}
Inc16.hdl
Inc16.hdl
CHIP Inc16 {
IN in[16];
OUT out[16];
PARTS:
// b=0000000000000001にする。1はtrue,0はfalseで表せる。
Add16(a=in, b[0] = true, b[1..15] = false, out=out);
}
ALU.hdl
ALU.hdl
CHIP ALU {
IN
x[16], y[16], // 16-bit inputs
zx, // zero the x input?
nx, // negate the x input?
zy, // zero the y input?
ny, // negate the y input?
f, // compute out = x + y (if 1) or x & y (if 0)
no; // negate the out output?
OUT
out[16], // 16-bit output
zr, // 1 if (out == 0), 0 otherwise
ng; // 1 if (out < 0), 0 otherwise
PARTS:
Mux16(a=x, b[0..15]=false, sel=zx, out=x0);
And16(a=x, b=x0, out=x1);
Not16(in=x1, out=notx1);
Mux16(a=x1, b=notx1, sel=nx, out=x2);
Mux16(a=y, b[0..15]=false, sel=zy, out=y0);
And16(a=y, b=y0, out=y1);
Not16(in=y1, out=noty1);
Mux16(a=y1, b=noty1, sel=ny, out=y2);
Add16(a=x2, b=y2, out=addxy);
And16(a=x2, b=y2, out=andxy);
Mux16(a=andxy, b=addxy, sel=f, out=xy);
Not16(in=xy, out=notxy);
Mux16(a=xy, b=notxy, sel=no, out[0..7]=out0, out[8..15]=out1);
Or16(a[0..7]=out0, a[8..15]=out1, b[0..15]=false, out=out);
Or8Way(in=out0, out=w0);
Or8Way(in=out1, out=w1);
Or(a=w0, b=w1, out=w2);
Not(in=w2, out=zr);
Or16(a[0..7]=true, a[8..15]=out1, b[0..15]=false, out[15]=ng);
}
3章 順序回路
- 組み合わせ回路
- AND,ORなどこれまで作成した回路のこと
- 入力値の組み合わせだけで値が確定する
- 状態(値)を保てないという欠点がある
- 記憶素子
- 時間経過してもデータを記録できる回路
- 記憶素子を備えた論理回路を順序回路と呼ぶ
- フリップフロップ
- 複雑な記憶素子の機能を備えたプリミィブな順序回路
- クロック
- 継続的に行き来する信号を全ての順序回路に送信する
- tick→tock→tick→tock…..
- tick→tockまでを周期(cycle)と呼ぶ
- 継続的に行き来する信号を全ての順序回路に送信する
- 2値素子(bit)・レジスタ
- データの格納呼び出しができる記憶装置
- レジスタはbitを並べたもの

- メモリ
- 任意の長さのワード(レジスタ)を記憶できるもの
- レジスタをたくさん積み重ねることでRAM(Random Access Memory)を構築できる
- RAMは物理的に存在する場所に関係なく、同じ時間で直接アクセスが可能となるようユニークなアドレスを割り振っている
- カウンタ
- タイムユニットが進むごとに値が加算される
- 一般的なCPUにはプログラムカウンタが含まれ、次に実行されるプログラム演算のアドレスとして解釈される
- 加算以外に値の設定とクリアが可能
chipのコードはここに置く
これ以降の投稿は「コンピュータシステムの理論と実装」に直接的に関係ない
2bit adderを作ってみた
circuit diagram


truth table
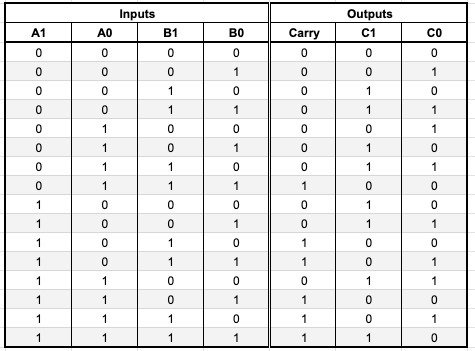
参考
開閉システム作ってみた
truth table

circuit diagram
1-to4 demultiplexerなし

1-to4 demultiplexerあり
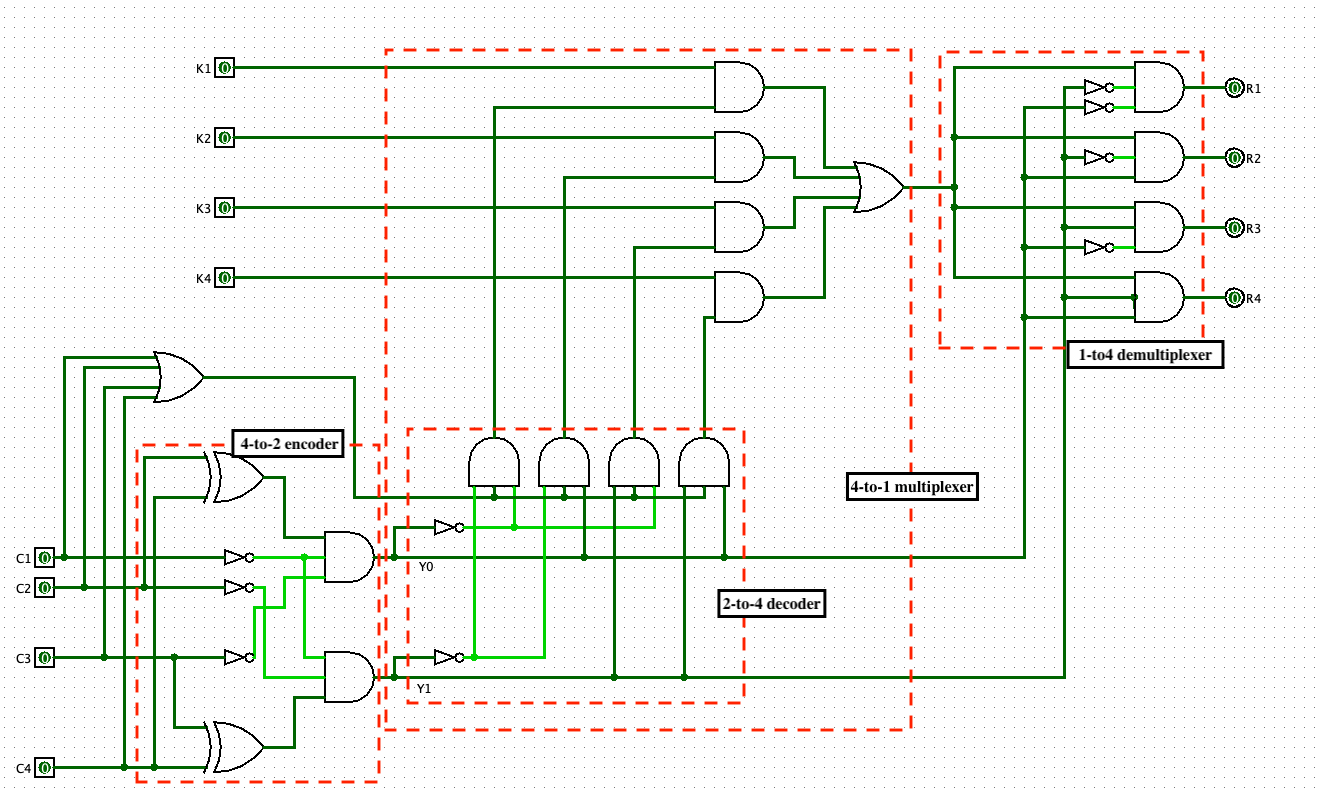
自販機販売システム
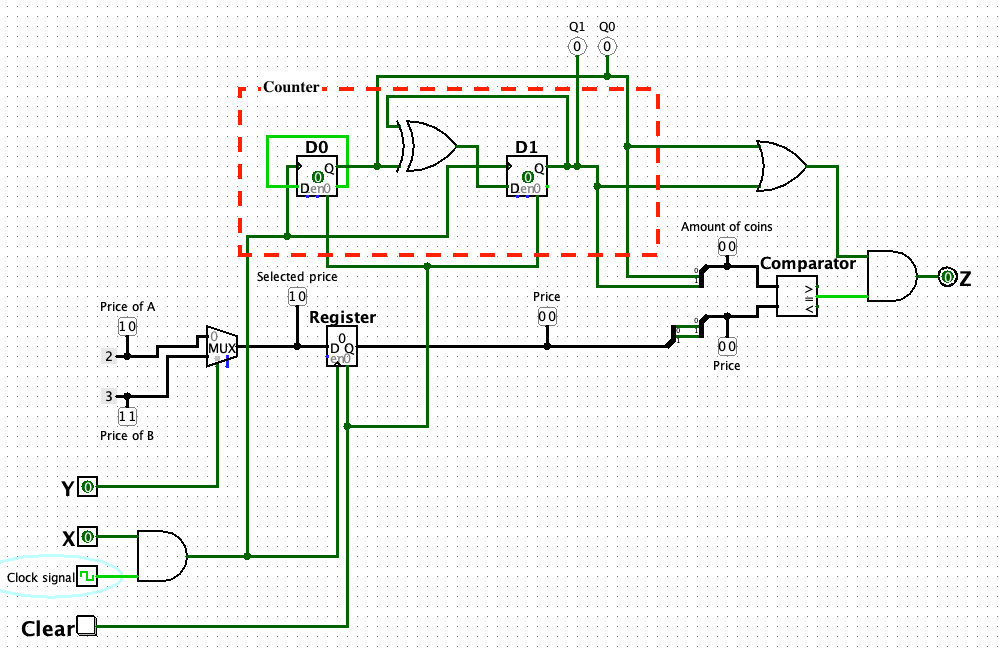
加算器
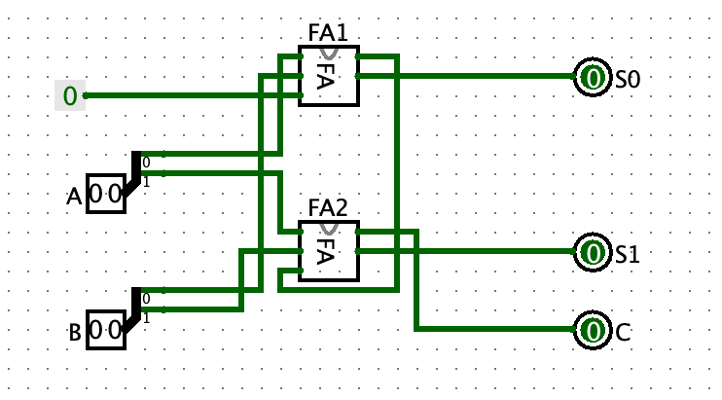
減算器

乗算器
除算器

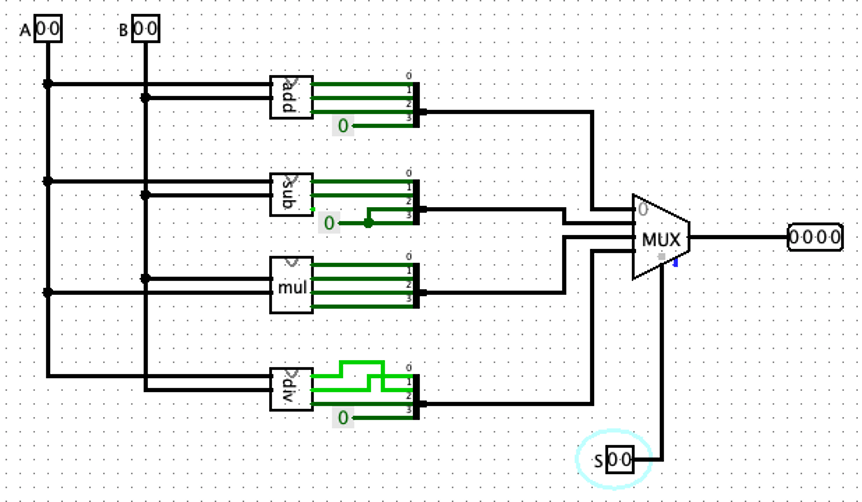
電卓
↑の演算器をモジュール化して作成
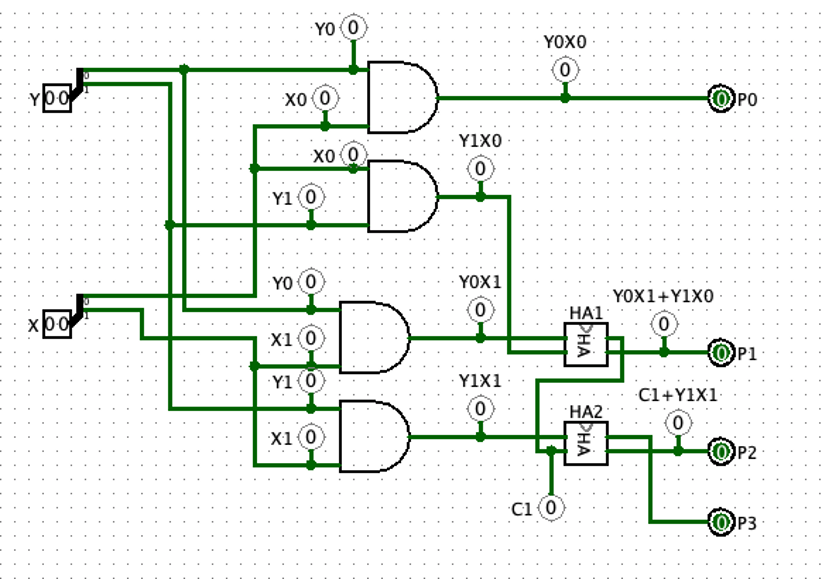
PLA使った2bit adder

このスクラップは2024/08/14にクローズされました