Statistical approaches for performance analysis

著者は Huawei Research 所属の Andrey Akinshin。以前は JetBrains で Perf. Engineer をやっていた。
dotnet 系の開発者で、dotnet/BenchmarkDotNet のプロジェクトリードをやっている。

Bad approaches

正規分布を想定するな。non-parametric な統計手法を使うべき。
帰無仮説による検定 (Null Hypothesis Significance Testing; NHST) を使うな。代わりにベイズ統計や Estimation statistics のような、変化量 (e.g. effect size) を扱える手法を使うべき。
ロバストでない統計量 (e.g. mean) を使うな。robust statistics (e.g. median) を使え。

Basic descriptive analysis

中心的傾向には中央値 (median) を使う
ノンパラメトリックな分布を扱う場合、中央値だけではなく複数の分位点 (quantile) を利用する
分位点の推定 (中央値含む) には、Harrell-Davis quantile estimator を使う
quantile を推定したら、Maritz-Jarrett 法で信頼区間 (confidence interval) を得る
分散傾向には**中央絶対偏差 (median absolute deviation)**を使う
95th, 99th, 99.9th percentile のような、極端な位置にある分位点の推定には**極値理論 (extreme value theory)**を利用する
ヒストグラムやカーネル密度推定 (KDE) のハイパーパラメータは、quantile (Harrel-Davis quantile estimator) を基に算出するとよい
外れ値に注意する
- 多峰 (multi-modal) な分布では、外れ値が中央にあることがある (intermodal outliers)
- Tukey's fences のような有名な手法だと、多峰分布に対応できない
- Harrell-Davis quantile estimator に基づく DoubleMAD outlier detector のような手法を活用するとよい
多峰性に注意する。

Comparing distributions

Q-Q プロットを書いた時の差分/比率を基に判定 shift and ratio functions
p 値 (p-value) だけではなく効果量 (effect size) を使う
- https://www.mizumot.com/method/mizumoto-takeuchi.pdf
- 著者は quantile-specific effect size なるものを考案している

Junya Yamaguchi (@openjny)

[Smith88] Characterizing Computer Performance with a Single Number

実行時間データの geometric mean を取ることには意味がない (実行時間の合計と整合しない) ことを主張

Junya Yamaguchi (@openjny)

Geometric Mean を使うのはやめておいた方がよいという主張。

$\mathrm{GM}(x/y)=\mathrm{GM}(x) / \mathrm{GM}(y)$ という性質から、正規化された値に関しては geometric mean の有益さが存在する。しかしながら、一般的にはこの性質は適用できない。

マシン/システムの構造は個々で異なるため、正規化の分母となりえる「リファレンスマシン/システム」を用意する発想自体が適切でない
ひとつのベンチマークのパフォーマンスが単一の実数で測れるとは限らない (分布を考慮すべき状況が多々ある)

さらに、以下の欠点がある。

ゼロの値を扱えない
小さい値では計算が安定しない
外れ値に頑健ではない (算術平均もまた頑健ではないものの)

Junya Yamaguchi (@openjny)

shift and ratio function

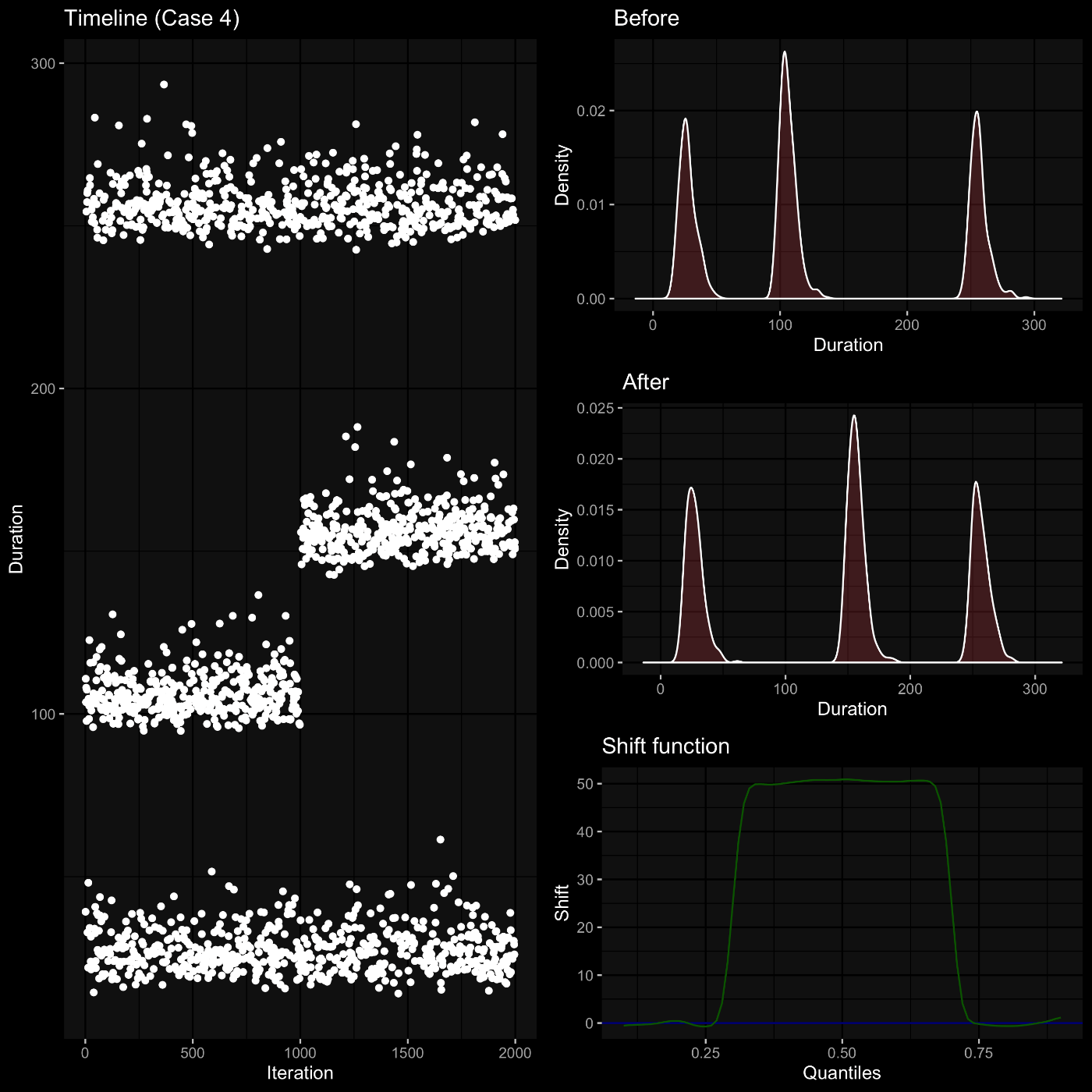
二つの分布に差分があるかを検査するノンパラメトリック手法。
分位点のシフト量/比率をプロットすることで、視覚的に差異を確認できる。
QQ-plot に似ている。

Junya Yamaguchi (@openjny)

効果量

Junya Yamaguchi (@openjny)

[JunSeong2012] A Case Study on Oscillating Behavior of End-to-End Network Latency

end-to-end latency を構成するもの

latency = t_d + t_s + t_q + t_f + t_p

$t_d$ : distance delay (propagation delay): 地理的な距離に比例して大きくなる電気信号の伝播遅延
$t_s$ : serialization delay: ネットワークインターフェイスが物理メディアに対して電気信号等を流し込む際の処理時間
$t_q$ : queuing delay: キューでの待機時間
$t_f$ : forwarding delay: ネットワークデバイスが宛先を決定したり、送信キューにパケットを挿入するのに要する時間
$t_p$ : protocol delay: エンドホストが送受信のアルゴリズムを実行するのに要する時間

理論的に言えば、ネットワークレイテンシを数学的に特徴づけることは可能。しかし、実際には、異なる管理組織によって運営されているネットワーク (AS) をいくつも跨ぐ事や、QoS やルーティングプロトコルの特性がそれぞれ異なることから、正確なモデルを作ることは極めて難しい。

Junya Yamaguchi (@openjny)

M/M/1

M/M/1 待ち行列 (M/M/1 queue) は、到着する要求がポアソン過程に従い、窓口が処理する時間が指数時間に従う待ち行列のこと。一列に並んだ要求を一つのサーバーが処理するのをモデル化した待ち行列といえる。

ポイント: 待ち行列の長さが一つ増えたり減ったりするのに要する時間が従う分布が指数分布であり、それぞれパラメータ $\lambda, \mu$ で表せる。指数分布のモーメントは解析的に求められので、例えば、キューがひとつ増える平均時間は $1/\lambda$ 、ひとつ減る平均時間は $1/\mu$ であることがわかる。

$\lambda$ : 平均到着率
$\mu$ : 平均サービス率

ケンドールの記号

A/B/C

A: 到着の過程: マルコフ過程 (指数分布) なら M
B: サービス時間の分布: マルコフ過程 (指数分布) なら M
C: サービスの数

より正確には、システムの容量 K、システムに来る客の最大数 N、サービス提供の順番 D をあわせて、A/B/C/K/N/D と書く。省略した場合は $K = \infty, N=\infty, D=FIFO$ 。

＃＃ルーターで考えるなら

$\lambda$ : パケットの到着レート (packets/sec)
$\mu$ : パケットの処理レート (packets/sec)

リトルの公式 (Littel's Law)

任意の待ち行列モデルに対して、定常状態 ( $M/M/1$ の場合だと、 $\rho = \lambda/\mu < 1$ かつ十分に時間経過した状態) なら、 $N=\lambda T$ が成立する。

where:

$\lambda$ : 単位時間当たりのパケット到着レート (pps)
$N$ : システムに含まれるパケット数の平均値
$T$ : あるパケットのキューイングから送信が終了するまでに要する時間 (レイテンシ) の平均値 (sec)

システム中のパケット数

定常状態だと、システム中のパケット数 $n$ が従う分布は、パラメータ $1-\rho$ の幾何分布 ( $\rho=\lambda/\mu$ ):

P(n)= (1-\rho)\rho^n

したがって、リトルの法則とあわせて以下を導ける。

システムに含まれるパケット数の平均 $N=E[n]$ は、 $\rho/(1-\rho)$
パケットの送信までに要する時間 (レイテンシ) の平均 $T$ は、 $1/(\mu-\lambda)$

遅延と帯域の関係

トラフィックの到着レート $\lambda$ と、トランスミッション容量 $\mu$ がそれぞれ 2 倍になった状況を想定する。

$\rho$ は変化しないので、システム内パケット数の平均 $N$ は変化なし
一方で、レイテンシの平均は $T = 1/(\mu-\lambda)$ は半分になる

例えば、高速ネットワーク環境では、end-to-end latency における伝播遅延 (propagation latency) の影響の方が相対的に大きくなることや、バッファーサイズの設定等は引き続き注意すべき項目となることがわかる。

Junya Yamaguchi (@openjny)

Turkey (1977) は、正規性が仮定できない場合など、データ分布が予め想定できない場合は、順序統計量を基礎とした統計量を分布位置やばらつきの推定に用いた。
代表的な統計量は、中央値、四分位値、四分位範囲 (IQR)。
箱ひげ図 (box-plot) を使用して可視化。

外れ値に関する話

異常値は、外れ値のサブセットである。
- 外れ値: 大部分の傾向と異るデータであり、必ずしも誤りとは限らないものの、データ集計や分析の際に結果の精度を悪化させる可能性があるもの
- 異常値: 測定ミス・記録ミスなどに起因して、真の分布からサンプルされなかったデータ。特異値とも言う
外れ値と異常値は、実用上区別できないこともある。