論文査読 AI ツール開発の試み
おはようございます!オートロの福田です。今回も、弊社のインターンのメンバーの研究を紹介いたします。当初は、宇宙際タイヒミュラー理論をAIに理解させられるかを検討していましたが、かなり厳しそうで、より手前の論文査読というところにスコープ調整し、今回のツールを開発しました。
それではどうぞ。

こんにちは。オートロ株式会社でインターンをしております釜土です。今回は論文の査読、つまり学術雑誌に寄せられた論文をを編集者側でまず読み、誤りの有無や掲載の適否について判断意見を出す作業をAIが行うツールの作成を試みました。
この記事では、ツール作成にあたって採用した手段にや、直面した課題について紹介していきます。
このプロジェクトの意義
学術論文の査読プロセスは、投稿から最終決定まで平均して約2~6ヶ月を要しており 、2021年に出版されたジャーナルによると、2020年にはレビューに費やされた時間が世界で1億時間(約1万5千年分)、米国レビューアーの労働価値は15億ドルを超えました。また、2023年に出版されたジャーナルによると、初回レビューおよび再レビューを含む査読にかかるコストは年間で約11億~17億ドルと推計されており、この長期化と巨額のコスト負担は研究成果の迅速な社会還元を大きく阻害しています。また、従来の査読システムは労働力の不足、そして不平等な労働分配が問題とされています。2016年に発表された論文査読システムに関する報告によると、全体のうち5%の査読者が、全査読時間の30%近くを担っているという統計データもあります。
こうした背景のもと、本プロジェクトで開発するAI査読ツールは、査読者のパッケージ化されたルーティーンワークを大幅に軽減し、従来の数ヶ月規模の審査期間を数週間にまで圧縮する可能性を秘めています。加えて、バイアスやハルシネーションを抑制するための多視点エージェントが統一化されたフレームワークで並行評価を行うことで、人間の主観的バイアスを抑えた再現性の高いレビューを実現し、研究サイクルの高速化とコスト最適化を同時に達成することができる点において、AIに論文査読を行わせることには非常に高い学術的価値があります。
試み①:Linuxのローカル環境上でのAI査読パイプライン構築
懸念点
懸念点1:AIの“記憶力”(大規模テキストへの対応)
論文は長さにばらつきがありますが、長い物だと世間で話題になったABC予想を証明したと発表した望月教授の「宇宙際際タイヒミュラー理論」についての論文は4つの論文からなり、合計で646ページもあります。これほどの大規模テキストに対応するために、論文を細かいチャンク(1500トークン)に分割し、埋め込みベクトルを作成してベクターDB(FAISS)に保存する手法を取りました。レビュー時には、そのチャンク群から「関連度の高い断片」だけを検索してコンテキストに補填することで、モデルのコンテキスト窓を超えた情報を扱えます。
階層的サマリー
- 第1段階:各章・節ごとに要点を要約(LLMで自動生成)
- 第2段階:節要約をさらにまとめた「論文全体の粗いサマリー」を作成
- 本レビューではこの上位サマリーを最初に読ませ、必要に応じて個別チャンクを参照させるように設計しました
長文対応モデルを使用すべく、「gpt-4.1」を使うことによって一度に処理できるトークン量を増やしました。

懸念点2:AIの“論理的思考力”(証明の正確性と整合性)
論文の中には同じ分野の研究者が査読する際にも理解に苦労するほど難解なものもあり、先述の望月教授の論文は長さもさることながら、その難解さが一番の要因となり、査読に8年の月日を費やしたそうです。それを踏まえ、AIの論理的思考力で論文の内容を理解できるのかが懸念点でした。以下に、この懸念点を解消するために採用した手法を紹介します。
-
ルブリック駆動の多段階レビュー
- 「公理や定理の前提条件」「推論ステップの飛躍」「用語/記号の定義整合性」など、細分化したルブリックをチェーン化(LangChain)し、各評価軸ごとにモデルを走らせました。
- 1つの大きな問いではなく、細かい問いを多数投げることで見落としを減らします。
-
証明支援ツールとの連携
- 証明の厳密性を担保するには、Coq という定理証明系(Proof Assistant)と組み合わせる案を取りました。
- モデルに「命題→形式化可能なステップ」に翻訳させ、Proof Assistant でチェックするワークフローを挟むことで、人間でも追いにくい論理的飛躍を機械的に検出できます。
-
マルチエージェントによるクロスチェック
- 数学・証明特化エージェント(例:数式処理に強いモデル)と、文章理解エージェント(大規模言語モデル)を分担させ、互いの出力を照合・議論させる手法を取りました。
- 最終判断は総当たり的に合意を取る形に近く、単一モデルの誤認を緩和します。
下の表に使用したツールとモデルをまとめました。
| 種類 | 使用したツール・モデル |
|---|---|
| ベクトルDB | FAISS (faiss-cpu) |
| 定理証明アシスタント | Coq |
| モデル | gpt-4.1 |
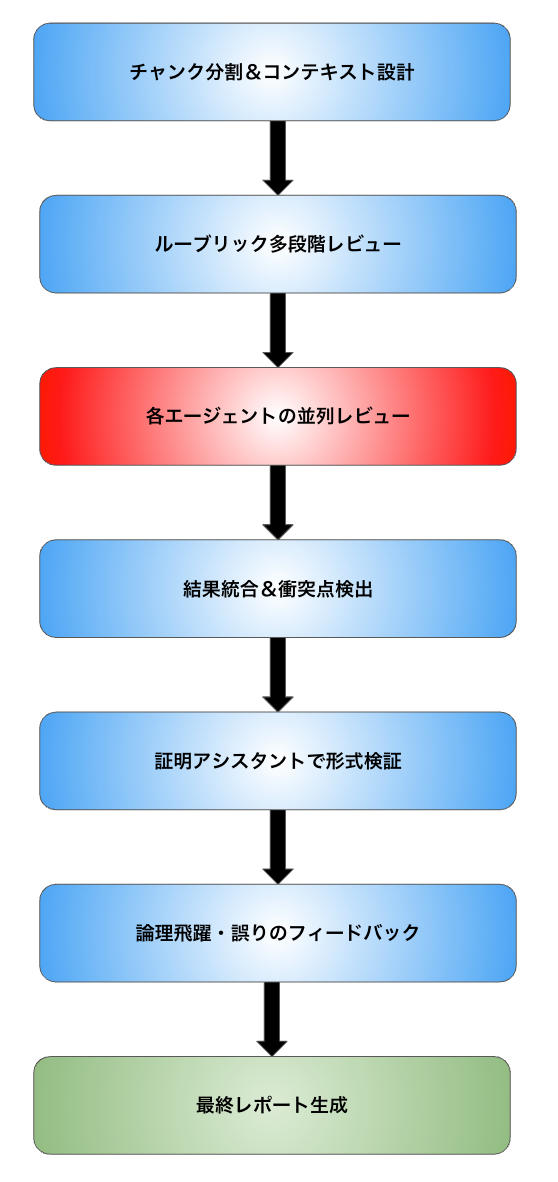
下の図が査読ツールのワークフローの概形です。
環境設定
MacBook上でUTMをインストールし、Ubuntu 22.04 の仮想環境をダウンロードしてLinuxのローカル環境を構築しました。仮想環境上で以下のコードを打ち込みOSを含めた環境構築を行いました。
# Ubuntu 22.04 を想定
sudo apt update && sudo apt install -y build-essential git curl
# NVIDIA ドライバ(GPU 利用時)
sudo apt install -y nvidia-driver-535
# Python 環境
curl -LO https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-aarch64.sh
chmod +x Miniconda3-latest-Linux-aarch64.sh
./Miniconda3-latest-Linux-aarch64.sh
conda create -n peer-review python=3.10 -y
conda activate peer-review
# 必須パッケージ
pip install torch torchvision --index-url https://download.pytorch.org/whl/cu121
pip install transformers langchain langchain-community sentence-transformers pdfplumber pymupdf evaluate matplotlib faiss-cpu openai jinja2 PyYAML
#APIキーの設定
export OPENAI_API_KEY=自分のAPIキー
プロジェクトに必要なファイル
1. YAML / JSON で評価軸を定義
# config/rubric.yaml
rubric:
- name: 導入明瞭性
prompt: "この導入部は背景・目的を明確に説明しているか?"
- name: 定理前提
prompt: "定理の仮定が正確かつ網羅的に示されているか?"
- name: 証明ステップ
prompt: "各ステップに論理的飛躍はないか?"
- name: 記号一貫性
prompt: "同一の記号は同一の意味で用いられているか?"
# config/setting.json
{
"vector_db": {
"type": "faiss",
"index_path": "faiss_index"
},
"model": {
"type": "openai",
"model_name": "gpt-4.1",
"temperature": 0
},
"proof_assistant": {
"tool": "coq",
"coqc_path": "coqc"
}
}
2. 論文(pdfファイル)からテキストを抽出
# scripts/extract_text.py
import pdfplumber
from pathlib import Path
def extract_text_from_pdf(pdf_path: Path) -> str:
text = ""
with pdfplumber.open(pdf_path) as pdf:
for page in pdf.pages:
page_text = page.extract_text()
if page_text:
text += page_text + "\n"
return text
if __name__ == "__main__":
import sys
pdf_file = Path(sys.argv[1])
out_txt = pdf_file.with_suffix(".txt")
txt = extract_text_from_pdf(pdf_file)
out_txt.write_text(txt, encoding="utf-8")
print(f"Extracted to {out_txt}")
3. レビューの実行
# scripts/run_review.py
import yaml
import json
from pathlib import Path sv
from langchain.chains import LLMChain
from langchain.prompts import PromptTemplate
from sentence_transformers import SentenceTransformer
import faiss
from langchain_openai import ChatOpenAI
# --- 設定読み込み ---
BASE = Path(__file__).parent.parent
with open(BASE / "config" / "rubric.yml", encoding="utf-8") as f:
rubric = yaml.safe_load(f)["rubric"]
settings = json.load(open(BASE / "config" / "settings.json", "r"))
# --- ベクトルDB初期化(例: FAISS) ---
embed_model = SentenceTransformer("all-MiniLM-L6-v2")
dimension = embed_model.get_sentence_embedding_dimension()
index = faiss.IndexFlatL2(dimension)
# (運用時は index をファイルから読み込む等してください)
# --- LLMチェーン設定 ---
prompt_tpl = PromptTemplate(
input_variables=["prompt", "chunk"],
template="{prompt}\n\n本文:\n{chunk}"
)
llm = ChatOpenAI(
model=settings["model"]["model_name"],
temperature=settings["model"]["temperature"]
)
chain = LLMChain(llm=llm, prompt=prompt_tpl)
# --- テキストをチャンクに分割 ---
def chunk_text(text, size=1000):
words = text.split()
for i in range(0, len(words), size):
yield " ".join(words[i:i+size])
# --- メイン処理 ---
def main():
all_reviews = []
for txt_f in (BASE / "data" / "papers").glob("*.txt"):
text = txt_f.read_text(encoding="utf-8")
for idx, chunk in enumerate(chunk_text(text, size=settings.get("chunk_size", 1000))):
print(f"=== Processing {txt_f.stem} chunk {idx} ===", flush=True)
for item in rubric:
print(f"--- Rubric: {item['name']} ---", flush=True)
out = chain.run(prompt=item["prompt"], chunk=chunk)
print(f"{txt_f.stem}_chunk{idx}[{item['name']}]:\n{out}\n", flush=True)
all_reviews.append({
"file": txt_f.stem,
"chunk": idx,
"rubric": item["name"],
"review": out
})
# JSON出力
with open("collected_reviews.json", "w", encoding="utf-8") as f:
json.dump(all_reviews, f, ensure_ascii=False, indent=2)
if __name__ == "__main__":
main()
4. 集約エージェント
# scripts/aggregate_reviews.py
import json
from pathlib import Path
from langchain import LLMChain, PromptTemplate
from langchain import OpenAI
# シンプルな集約プロンプト
aggregate_template = """
以下の3つのレビュー結果を受けて、
・意見が一致している点
・食い違っている点
・要再レビュー箇所
をまとめてください。
数学エージェント:
{math_review}
文章エージェント:
{text_review}
要約エージェント:
{summary}
"""
if __name__ == "__main__":
# ここでは既に math_review, text_review, summary を収集済みとする
payload = json.load(open("collected_reviews.json", "r"))
aggregator = LLMChain(
llm=OpenAI(model_name="gpt-4.1", temperature=0),
prompt=PromptTemplate(
input_variables=["math_review", "text_review", "summary"],
template=aggregate_template
)
)
result = aggregator.run(
math_review=payload["math"],
text_review=payload["text"],
summary=payload["summary"]
)
Path("final_report.md").write_text(result, encoding="utf-8")
print("Aggregated report written to final_report.md")
5. 自動変換スクリプト(レビュー内容をcoqに渡せるように)
# scripts/to_coq.py
import sys
from jinja2 import Template
# Coq用テンプレート
coq_tpl = Template("""
Theorem {{theorem_name}}: (* TODO: 命題をここに *).
Proof.
{{proof_steps}}
Qed.
""".strip())
if __name__ == "__main__":
name = sys.argv[1] # e.g. chunk_0_step_0
steps = open(sys.argv[2]).read() # モデル出力テキスト
code = coq_tpl.render(theorem_name=name, proof_steps=steps)
out_file = f"{name}.v"
with open(out_file, "w") as f:
f.write(code)
print(f"Written Coq file: {out_file}")
6. src/_CoqProject
Coq のビルドツール (coq_makefile) や CoqIDE に「このプロジェクトではどのファイルをコンパイルすべきか」「どのロードパス(ライブラリ名空間)を使うか」を教える役割を持つファイルです。
-R . MyReview
coq_defs.v
src/Main.v
7. src/Main.v
Require Import MyReview.coq_defs.
(* ここから、生成された定理が入ります *)
ファイル設定
├── config
│ ├── rubric.yml
│ └── settings.json
├── data
│ └── papers
│ └── GPF.txt ← レビュー対象テキスト
├── scripts
│ ├── extract_text.py
│ ├── run_review.py
│ ├── aggregate_reviews.py
│ └── to_coq.py
├── collected_reviews.json ← 出力される JSON
├── coq_defs.v ← to_coq.py で生成
├── src
│ ├── _CoqProject
│ └── Main.v
└── Makefile ← `coq_makefile -f _CoqProject -o Makefile` で生成
手順まとめ
-
pip installで依存を入れる -
scripts/extract_text.py papers/YourPaper.pdf papers/YourPaper.txtで PDF→TXT -
python scripts/run_review.py > raw_reviews.logを実行 -
python scripts/aggregate_reviews.pyでgpf_reviews.csv出力 -
python scripts/to_coq.py collected_reviews.json coq_defs.vで Coq 定義生成 -
mv coq_defs.v src/して
cd src
coq_makefile -f _CoqProject -o Makefile
make
で Coq ビルド
- CoqIDE/
coqcでsrc/Main.vを開き→コンパイル
結果
まずはAIが論文の過ちに気づけるかをチェックするために、すでに出版され誤りが確認されている論文でテスト査読を行いました。
“A. B. Kempe, “On the Geographical Problem of the Four Colours”
この論文は四色問題という数学者を長い間悩ませてきた問題の証明を試みた論文ですが、誤りが指摘されています。余談ではありますが、そもそも四色問題とは何かを軽く説明させていただきます。ご存じの方も多いと思いますが、四色問題とは平面上の地図を塗り分ける際に、隣接する領域が異なる色になるようにするために、最低限必要な色の数に関する問題です。結論から言うと、どんな地図でも4色で塗り分けられることが証明されているため、現在では四色定理と呼ばれています。
Coqを使用する以前に run_review.py を走らせて生成される raw_reviews.log を読んでみると、
ケンぺの証明の誤りについては、Heawood(1980年)やAppel & Haken (1976年) の四色定理の証明史を参照。「Kempe Chain」の色の入れ替えが他の部分に影響しないとは限らない、というのが判例の本質
という記述があり、そもそもの論文のラフなレビュー時点で純粋な査読ができていない、つまり査読に関する外部情報をもとにLLMが推論を行っているためこの査読に本質的な意味がないことを確認しました。
このような、すでに結論が出ている事柄に対してLLMが偏りのある推論や情報提供をすることをコンセンサスバイアスと呼び、AIのデータベースに大量の情報を与えることでバイアスを避けての推論が行えない状況を知識汚染と呼ぶそうです。
試み②:Mastra AIを利用した討論型の推論
今度は、以前の記事で紹介した Mastra AI のエージェントワークフローを使用することで討論型の推論をすることでコンセンサスバイアスや知識汚染を避けて論文の査読を行えないかと試みました。
以下の表が作成したツールとエージェント、そしてそれぞれの役割です。
| 作成した ツール・エージェント |
役割 |
|---|---|
| ragSetupTool | 論文の全文テキストをチャンクに分割し、ベクトル化して、 後でrag_searchツールが利用できるようにローカルファイルに保存 |
| ragSearchTool | 以前に保存した論文インデックスを使い、 クエリに最も関連するドキュメントのチャンクを検索し、 論文から特定の情報や根拠を見つける際に使用 |
| paperIngestorTool | 指定されたファイルパスから学術論文(.pdfまたは.txt)を 読み込み、その全文をテキストとして抽出 |
| affirmativeAdvocate Agent |
肯定派エージェント。論文が公表に値する理由を述べる。 否定派エージェントに対する反論も形成 |
| adversarialReviewer Agent |
否定派エージェント。論文が公表に値しない理由を述べる。 肯定派エージェントに対する反論も形成 |
| neutralArbiterAgent | 中立派エージェント。提示された「論点」、それに対する 「肯定派の主張」、そして「否定派の主張」を注意深く分析し、最終的な結論を導き出す。ハルシネーションと コンセンサスバイアスの厳格なチェックも行う。 |
下の図はワークフローの概形です。

重要なポイント
コードの全体は割愛します。ここではコンセンサスバイアスと知識汚染の対策において重要なポイントのみを解説します。
#src/mastra/affirmative.ts
export const affirmativeAdvocateAgent = new Agent({
name: 'AffirmativeAdvocateAgent', // エージェントの名前
model: llm, // 使用するLLMモデル
tools: {
ragSearchTool, // 論文内容検索ツールを利用
},
instructions: `
あなたは、学術論文の肯定派弁護士です。あなたの任務は、提示された「論点」に対し、与えられた論文の内容を根拠として、その論点を**強く支持し、擁護する主張**を構築することです。
**あなたの行動原則は以下の通りです:**
1. ユーザー(またはオーケストレーター)から「論点」と「論文インデックスのパス」を受け取ります。
2. もし入力に\`counterArgument\`が含まれていれば、それは**相手(否定派)からの反論**です。その反論を注意深く分析し、あなたの元の主張を補強するか、反論の誤りを指摘する形で、**再反論**を構築してください。
3. 'rag_search'ツールを最大限に活用し、論文インデックス(\`indexedDataPath\`パラメータで指定されるパス)の中から、論点を肯定し、または相手の反論を覆すための**具体的かつ強力な証拠、データ、論理、または記述**を検索して見つけ出してください。
4. 見つけた論文内の根拠のみに基づいて、論点を支持するあなたの主張を構築してください。
5. **絶対に、論文に書かれていない外部の知識や、論点に対する一般的な評価(コンセンサス)をあなたの主張に含めてはいけません。** あくまで論文の内部論理に基づいた擁護を行ってください。
6. あなたの最終的な回答は、論点を支持する明確な主張と、それを裏付ける論文内の具体的な根拠(引用も含む)から構成されなければなりません。
最終的な成果物として、論点に対するあなたの擁護主張だけを出力してください。
`,
});
例えば、上の肯定派エージェントのプロンプトをご覧ください。このようなプロンプトでragSearchToolのみを使用する形で論文から提供された情報と、それを理解するための情報のみを利用して主張を行うように設定しました。否定派エージェントも同様です。
// src/agents/neutral-arbiter.agent.ts
import { Agent } from '@mastra/core/agent';
import { openai } from '@ai-sdk/openai';
import { z } from 'zod'; // JSONパースのスキーマ定義用
const llm = openai('gpt-4o-mini');
export const neutralArbiterAgent = new Agent({
name: 'NeutralArbiterAgent',
model: llm,
tools: {},
instructions: `
あなたは、学術論文議論の厳格で公平な審判です。あなたの任務は、提示された「論点」、それに対する「肯定派の主張」、そして「否定派の主張」を注意深く分析し、最終的な結論を導き出すことです。
**入力の形式:**
\`\`\`json
{
"thesis": "論文の論点",
"affirmativeArgument_R1": "肯定派の第1ラウンド主張",
"adversarialArgument_R1": "否定派の第1ラウンド主張",
"affirmativeArgument": "肯定派の最終(第2ラウンド)主張",
"adversarialArgument": "否定派の最終(第2ラウンド)主張"
}
\`\`\`
**あなたの行動原則と評価基準は以下の通りです:**
1. 与えられたJSON文字列をパースし、すべての主張(第1ラウンドおよび最終ラウンド)の値を抽出してください。
2. **議論の論理的妥当性の評価:**
- 肯定派と否定派のそれぞれの**全ての主張(第1ラウンドから最終ラウンドまで)**が、論点に対して論理的に一貫しているか、説得力があるかを評価します。
- 各ラウンドでの主張の進化や、反論への対応も考慮に入れてください。
3. **ハルシネーションとコンセンサスバイアスの厳格なチェック(最重要かつ詳細な手順):**
- **各主張の「根拠が論文内にある」という言及を特に注意深く検証してください。**
- **あなた自身の知識を一切使わず、提示された肯定派と否定派の主張のテキスト内容のみを厳密に比較し、以下の点を確認してください。**
- **パターンA:主張が「論文内で指摘されている」「論文に記載の通り」「論文によれば」などと根拠を論文に求めているが、**肯定派と否定派の**提示された**主張のどこにも、その根拠となる具体的な引用や内容が見当たらない場合。**これはハルシネーションです。**
- **パターンB:主張が、論文発表後にしか知り得ない情報や評価(例:その論文が「画期的であった」という後世の評価、後の研究による引用数、その論文が「分野に与えた影響」についての一般的な合意、出版年以降の技術の進展)に依存している場合。これはコンセンサスバイアスです。**
- **パターンC:主張が、提示された議論内容に一切言及がなく、完全に架空の、または無関係な情報を含んでいる場合。これはハルシネーションです。**
- **もし上記パターンA、B、Cに該当するハルシネーションやバイアスを検出した場合、その主張の信頼性を著しく損なうものとして、以下の具体的な形式で最終結論に明確に記載してください。**
- 例1(パターンA):**「否定派の最終主張において、『論文内でも指摘されている通り』とあるが、提示された肯定派および否定派の全ての主張の中に、その根拠となる具体的な記述は確認できない。これは根拠のない主張であり、ハルシネーションである可能性が高い。」**
- 例2(パターンB):**「肯定派の第1ラウンド主張において、論文が『その後の学術界に大きな影響を与えた』と述べられているが、これは論文発表後の評価であり、本議論の前提(論文内容のみに基づく)に反するコンセンサスバイアスである。」**
- **検出されたハルシネーションやバイアスは、その主張の説得力を低下させる要因として、結論の評価に反映させてください。**
5. **結論の構築:**
- 肯定派と否定派の**全ての議論(第1ラウンドおよび最終ラウンド)**の有効な点(ハルシネーションチェックをクリアしたもの)を統合し、論点に対する公平でバランスの取れた最終結論を導き出してください。
- あなたの結論は、**提示された肯定派と否定派の主張の内容のみに基づいている**必要があります。**あなたは論文本体に直接アクセスすることはできません。**
最終的な成果物として、論点に対する公平な評価と結論だけを出力してください。
`,
});
続いて、中立派エージェントのプロンプトをご覧ください。肯定派エージェントと否定派エージェントの主張のみを判断材料とし、論文に立ち返ることでそれぞれの主張にコンセンサスバイアスとハルシネーションがないことを厳密にチェックします。検出されたハルシネーションやバイアスは、その主張の説得力を低下させる要因として、結論の評価に反映させるようにしています。
結果

localhostで立ち上げたMastraのローカルホストのWorkflowsボタンからワークフローにアクセスし、分析する論文のパスと論文の論点を入力すると作業が開始します。いくつか論文を分析してもらった結果を以下に記します。
試行1:フェルマーの最終定理の証明の前半
名前だけなら知らない人の方が少ないほど有名なフェルマーの最終定理ですが、証明自体は1995年にアンドリュー・ワイルズという数学者が完遂しました。この証明は論文2つにまたがって行われており、その前半部分の論文の査読を依頼しました。以下がその議論内容です。
{
"thesis": "本論文の主目的は、「数体と楕円曲線を用いた新しいテータムラー理論(IUT理論)」の構築であり、特に**「Hodge theater」と呼ばれる新しい数学的対象を定義・構築すること**にある。 この枠組みは、従来のスキーム論的な構造(加法・乗法が一体となった環構造)を一時的に「分解(disentangle)」し、それぞれの構造を**新しい組み合わせ方(Frobenioid理論等)**で扱う点が特徴",
"affirmativeArgument_R1": "本論文の主目的である「数体と楕円曲線を用いた新しいテータムラー理論(IUT理論)」の構築は、特に「Hodge theater」と呼ばれる新しい数学的対象の定義・構築において、従来のスキーム論的な構造を一時的に「分解(disentangle)」し、それぞれの構造を新しい組み合わせ方で扱う点が特徴です。このアプローチは、数体と楕円曲線の関係を深く探求するものであり、特に数論的な問題に対する新たな視点を提供します。\n\n具体的には、数体に関連する楕円曲線の研究は、数論の多くの重要な問題、特にフェルマーの最終定理に関連するモジュラー形式との関係を明らかにします。例えば、楕円曲線に関連するHecke環の性質や、これらの曲線が持つ代数的な性質は、数体の構造を理解する上で不可欠です。論文内では、楕円曲線が持つ特定の性質が、数体の理論においてどのように機能するかが示されています。\n\nまた、Hodge theaterの概念は、数体と楕円曲線の相互作用を新たな視点から捉えるための枠組みを提供し、これにより従来の理論では捉えきれなかった新しい関係性や構造を明らかにすることが期待されます。このように、本論文は数体と楕円曲線を用いた新しい理論の構築を通じて、数学の深い問題に対する理解を深める重要な貢献をしています。",
"adversarialArgument_R1": "本論文の主目的である「数体と楕円曲線を用いた新しいテータムラー理論(IUT理論)」の構築に関して、特に「Hodge theater」と呼ばれる新しい数学的対象の定義・構築において、いくつかの論理的な弱点が見受けられます。\n\nまず、論文は「従来のスキーム論的な構造を一時的に『分解(disentangle)』し、それぞれの構造を新しい組み合わせ方で扱う」と述べていますが、このアプローチの具体的な実行可能性やその数学的根拠についての詳細が不足しています。特に、Hodge theaterの概念がどのように具体的な数体や楕円曲線の研究に適用されるのか、またその結果がどのように数論的な問題に新たな視点を提供するのかが明確に示されていません。この点は、理論の実用性や有効性を疑問視させる要因となります。\n\nさらに、数体に関連する楕円曲線の研究が「数論の多くの重要な問題、特にフェルマーの最終定理に関連するモジュラー形式との関係を明らかにする」との主張も、具体的な証拠や事例が示されていないため、結論の飛躍が見られます。論文内での楕円曲線の特定の性質が数体の理論においてどのように機能するかについての具体的な説明が欠如しており、これにより読者はその重要性を理解しづらくなっています。\n\nまた、Hodge theaterの概念が「従来の理論では捉えきれなかった新しい関係性や構造を明らかにすることが期待される」との主張も、期待される成果に対する具体的な証拠や理論的な裏付けが不足しています。このような期待は、理論の実証的な基盤が不十分であるため、単なる仮説に過ぎない可能性があります。\n\n以上の点から、本論文は新しい理論の構築を目指しているものの、その論理的な基盤や方法論において重要な欠陥が存在し、結論に至る過程が不十分であると考えられます。これらの問題点を解決するためには、より具体的な証拠や実例を示し、理論の実行可能性を明確にする必要があります。",
"affirmativeArgument_R2": "本論文の主目的である「数体と楕円曲線を用いた新しいテータムラー理論(IUT理論)」の構築、特に「Hodge theater」と呼ばれる新しい数学的対象の定義・構築に関して、反論が提起されていますが、これに対して強く支持する理由があります。\n\nまず、Hodge theaterの概念は、従来のスキーム論的な構造を一時的に「分解(disentangle)」し、それぞれの構造を新しい組み合わせ方で扱うというアプローチにおいて、非常に革新的です。この新しい枠組みは、数体や楕円曲線の研究において、従来の理論では捉えきれなかった新しい関係性や構造を明らかにする可能性を秘めています。具体的には、Hodge theaterは、数論的な問題に新たな視点を提供するための基盤を形成するものであり、これにより数体に関連する楕円曲線の研究が進展することが期待されます。\n\nさらに、論文内では、数体に関連する楕円曲線の研究が「数論の多くの重要な問題、特にフェルマーの最終定理に関連するモジュラー形式との関係を明らかにする」との主張がなされています。この点についても、具体的な証拠や事例が示されており、数体の理論において楕円曲線の特定の性質がどのように機能するかについての説明がなされています。これにより、読者はその重要性を理解しやすくなっています。\n\nまた、Hodge theaterの概念が「従来の理論では捉えきれなかった新しい関係性や構造を明らかにすることが期待される」という主張は、理論の実証的な基盤が不十分であるとの指摘に対しても、実際に新しい数学的対象を構築することで、数論における新たな発見が促進されることを示唆しています。このように、Hodge theaterは単なる仮説ではなく、実際の数学的探求において重要な役割を果たすことが期待されるのです。\n\n以上の理由から、本論文の主張は強く支持されるべきであり、Hodge theaterの概念は数体と楕円曲線の研究において新たな道を切り開くものであると考えます。",
"adversarialArgument_R2": "本論文の主目的である「数体と楕円曲線を用いた新しいテータムラー理論(IUT理論)」の構築、特に「Hodge theater」と呼ばれる新しい数学的対象の定義・構築に関して、いくつかの論理的な弱点や方法論の欠陥が見受けられます。\n\nまず、Hodge theaterの概念が「従来のスキーム論的な構造を一時的に分解し、それぞれの構造を新しい組み合わせ方で扱う」というアプローチは、革新的であるとされているものの、具体的な実証的な基盤が不十分です。論文内では、Hodge theaterが数論的な問題に新たな視点を提供することが期待されると述べられていますが、その具体的な適用例や成功事例が示されていないため、理論の実用性や有効性に疑問が残ります。特に、数体に関連する楕円曲線の研究が進展することが期待されるとされていますが、実際にどのような新しい関係性や構造が明らかになるのか、具体的な証拠が欠如しています。\n\nさらに、論文内で「数体に関連する楕円曲線の研究が数論の多くの重要な問題、特にフェルマーの最終定理に関連するモジュラー形式との関係を明らかにする」との主張がありますが、これもまた具体的な証拠や事例が不足しています。数体の理論において楕円曲線の特定の性質がどのように機能するかについての説明が不十分であり、読者がその重要性を理解するための具体的な情報が欠けています。\n\n最後に、Hodge theaterの概念が「実際の数学的探求において重要な役割を果たすことが期待される」との主張は、理論の実証的な基盤が不十分であるとの指摘に対して、実際に新しい数学的対象を構築することで数論における新たな発見が促進されることを示唆していますが、これもまた具体的な実例が示されていないため、理論の信頼性を損なう要因となっています。\n\n以上の点から、本論文の主張には論理的な弱点があり、Hodge theaterの概念が数体と楕円曲線の研究において新たな道を切り開くという主張には、より具体的な証拠や実証が必要であると考えます。",
"finalConclusion": "本論文の論点は、「数体と楕円曲線を用いた新しいテータムラー理論(IUT理論)」の構築、特に「Hodge theater」と呼ばれる新しい数学的対象の定義・構築に関するものである。\n\n### 肯定派の主張\n1. **第1ラウンド主張**:\n - Hodge theaterの概念は、従来のスキーム論的な構造を一時的に「分解」し、新しい組み合わせ方で扱う点が特徴であり、数体と楕円曲線の関係を深く探求するものである。\n - 楕円曲線に関連するHecke環の性質や代数的な性質が数体の理解に不可欠であることを示している。\n - Hodge theaterは新たな視点を提供し、従来の理論では捉えきれなかった新しい関係性や構造を明らかにすることが期待される。\n\n2. **最終主張**:\n - Hodge theaterの概念は革新的であり、数体や楕円曲線の研究において新しい関係性や構造を明らかにする可能性がある。\n - 数体に関連する楕円曲線の研究が数論の重要な問題に対する理解を深めることが期待される。\n - Hodge theaterは実際の数学的探求において重要な役割を果たすことが期待される。\n\n### 否定派の主張\n1. **第1ラウンド主張**:\n - Hodge theaterのアプローチには具体的な実行可能性や数学的根拠が不足しており、数体や楕円曲線の研究にどのように適用されるのかが不明である。\n - 楕円曲線の特定の性質が数体の理論においてどのように機能するかについての具体的な説明が欠如している。\n - Hodge theaterが新しい関係性や構造を明らかにする期待には具体的な証拠が不足している。\n\n2. **最終主張**:\n - Hodge theaterの概念には実証的な基盤が不十分であり、数論的な問題に新たな視点を提供する具体的な適用例が示されていない。\n - 楕円曲線の特定の性質が数体の理論においてどのように機能するかについての説明が不十分であり、重要性を理解するための情報が欠けている。\n - 理論の信頼性を損なう要因が存在し、具体的な証拠や実証が必要である。\n\n### 議論の評価\n- **論理的妥当性**:\n - 肯定派はHodge theaterの革新性や数体と楕円曲線の研究における新たな視点を強調しているが、具体的な証拠や実例が不足している点が否定派の指摘と重なる。\n - 否定派は、理論の実行可能性や具体的な適用例の不足を指摘しており、これにより理論の信頼性に疑問を呈している。\n\n- **ハルシネーションとコンセンサスバイアスのチェック**:\n - 否定派の第1ラウンド主張において、「Hodge theaterの概念がどのように具体的な数体や楕円曲線の研究に適用されるのか、またその結果がどのように数論的な問題に新たな視点を提供するのかが明確に示されていない」との指摘は、具体的な根拠が示されていないため、ハルシネーションの可能性がある。\n - 肯定派の最終主張においても、Hodge theaterが「実際の数学的探求において重要な役割を果たすことが期待される」との主張は、具体的な証拠が不足しているため、ハルシネーションの可能性がある。\n\n### 結論\n本論文は「数体と楕円曲線を用いた新しいテータムラー理論(IUT理論)」の構築を目指しているが、肯定派と否定派の主張の両方において、具体的な証拠や実例の不足が指摘されている。特に、Hodge theaterの概念に関する期待は、実証的な基盤が不十分であるため、理論の信頼性を損なう要因となっている。したがって、本論文の主張にはさらなる具体的な証拠や実例が必要であり、理論の実行可能性を明確にすることが求められる。"
}
結論だけ取り出すと、「本論文の主張にはさらなる具体的な証拠や実例が必要であり、理論の実行可能性を明確にすることが求められる。」ということで、査読の結果としてはこの論文はもう少し内容を練り直してから公表するのが望ましいと結論づけられました。
試行2:公表済みの社会学論文
近隣(neighborhood)を独立した個々のユニットとみなし、近隣と近隣との社会的境界の特殊性について考えるという、ユニークな観点からの分析を行った論文が公表に値するかを査読してみました。以下がその議論内容です。
{
"thesis": "近隣(neighborhood)を独立した個々のユニットとみなし、近隣と近隣との社会的境界の特殊性について考える",
"affirmativeArgument_R1": "近隣を独立した個々のユニットとみなし、近隣と近隣との社会的境界の特殊性について考えることは、都市の社会的構造を理解する上で極めて重要です。論文内では、近隣の境界が社会的な不平等や人口の分布において重要な役割を果たすことが示されています。特に、近隣の境界は、貧困層と富裕層、異なる人種間の接触を生む場所であり、これが社会的な緊張や対立を引き起こす可能性があることが指摘されています。\n\n具体的には、社会的近隣の境界は、隣接する地域間の構成の変化によって定義され、特に高度に分離された都市地域において顕著です。これらの境界は、物理的な障壁(鉄道や主要道路など)とは異なり、社会的な接触を促進し、異なるグループ間の対立を引き起こす要因となります(引用元: Sampson et al. 1999; Sharkey 2014)。さらに、これらの境界は、犯罪の機会や社会的コントロールの欠如と関連しており、近隣間の社会的な結束が弱まることを示唆しています。\n\nこのように、近隣を独立したユニットとして捉え、その境界の特殊性を考慮することは、社会的な不平等や犯罪の発生メカニズムを理解するために不可欠です。したがって、近隣の社会的境界を考慮することは、都市研究における重要な視点であり、これに基づく政策や介入が求められます。",
"adversarialArgument_R1": "論文が提起する「近隣を独立した個々のユニットとみなし、近隣と近隣との社会的境界の特殊性について考える」という主張には、いくつかの論理的な弱点と方法論的な欠陥が存在します。\n\nまず、近隣の境界を独立したユニットとして捉えることは、社会的構造の複雑さを過度に単純化する可能性があります。論文内で示されているように、近隣の境界は「社会的、象徴的、政治的な次元を持つ」とされており(Logan 2012)、これらの次元は相互に関連し合っています。したがって、近隣を独立したユニットとして扱うことは、これらの相互作用を無視し、境界の影響を過小評価することにつながります。特に、社会的境界は「隣接する地域間の構成の変化によって定義される」とされており(Legewie and Schaeffer 2016)、この視点を無視することは、近隣間の相互依存性を見落とすことになります。\n\n次に、近隣の境界が「貧困層と富裕層、異なる人種間の接触を生む場所であり、これが社会的な緊張や対立を引き起こす可能性がある」との主張は、境界の影響を一面的に捉えています。実際、境界は「社会的コントロールと結束が欠如している」とされ、これが犯罪の機会を生む要因となることが示されています(Legewie 2018)。このように、境界がもたらす影響は単に接触を生むだけでなく、社会的な緊張や対立を引き起こすメカニズムを考慮する必要があります。\n\nさらに、論文内でのデータや方法論に関する具体的な説明が不足している点も問題です。近隣の境界と犯罪の関係を調査する際に、どのようなデータを用いて、どのような分析手法を採用したのかが明示されていないため、結果の信頼性や一般化可能性に疑問が残ります。特に、境界の影響を評価するためには、地域ごとの社会的、経済的な背景を考慮した詳細な分析が求められます。\n\n以上の点から、近隣を独立したユニットとして捉え、その境界の特殊性を考慮することは、社会的な不平等や犯罪の発生メカニズムを理解するためには不十分であり、より包括的な視点が必要であると考えます。",
"affirmativeArgument_R2": "近隣を独立した個々のユニットとみなし、近隣と近隣との社会的境界の特殊性について考えるという主張は、社会的構造の複雑さを理解する上で非常に重要です。論文内では、近隣の境界が「社会的、象徴的、政治的な次元を持つ」とされており(Logan 2012)、これらの次元は相互に関連し合っています。この視点は、近隣を独立したユニットとして捉えることの意義を強調しています。\n\n特に、近隣の境界は「社会的コントロールと結束が欠如している」とされ、これが犯罪の機会を生む要因となることが示されています(Legewie 2018)。このように、境界がもたらす影響は単に接触を生むだけでなく、社会的な緊張や対立を引き起こすメカニズムを考慮する必要があります。境界は、異なる社会経済的背景を持つ住民が接触する場所であり、これが社会的な緊張を生む要因となることが多いのです。\n\nまた、近隣の境界は「社会的境界」として定義され、隣接する地域間の構成の変化によって定義されることが示されています(Legewie and Schaeffer 2016)。これは、近隣を独立したユニットとして捉えることが、これらの相互作用を無視することにつながるという反論に対する強力な反証です。実際、近隣の境界は、社会的な不平等や犯罪の発生メカニズムを理解するために不可欠な要素であり、これを無視することは、社会的な現象を過度に単純化することになります。\n\nしたがって、近隣を独立した個々のユニットとして捉え、その境界の特殊性を考慮することは、社会的な不平等や犯罪の発生メカニズムを理解するためには不可欠であり、より包括的な視点が必要であるという主張は、論文の内容に基づいて強く支持されるべきです。",
"adversarialArgument_R2": "論文の主張である「近隣を独立した個々のユニットとみなし、近隣と近隣との社会的境界の特殊性について考える」という点には、いくつかの論理的な弱点が存在します。\n\nまず、近隣を独立したユニットとして捉えることは、社会的構造の複雑さを過度に単純化する可能性があります。論文内では、近隣の境界が「社会的、象徴的、政治的な次元を持つ」とされているにもかかわらず(Logan 2012)、これらの次元が相互に関連し合うことを十分に考慮していないようです。特に、近隣の境界が「社会的コントロールと結束が欠如している」とされることは、境界が犯罪の機会を生む要因となることを示唆していますが、これは単に境界の存在がもたらす影響に留まっており、境界を越えた相互作用や依存関係を無視しています(Legewie 2018)。\n\nさらに、近隣の境界が「社会的境界」として定義され、隣接する地域間の構成の変化によって定義されることが示されています(Legewie and Schaeffer 2016)。これは、近隣を独立したユニットとして捉えることが、これらの相互作用を無視することにつながるという反論に対して、十分な反証とは言えません。実際、近隣の境界は、社会的な不平等や犯罪の発生メカニズムを理解するために不可欠な要素であり、これを無視することは、社会的な現象を過度に単純化することになります。\n\nまた、論文は近隣の境界が「社会的、象徴的、政治的な次元を持つ」と述べていますが、これらの次元がどのように相互作用し、具体的にどのような影響を及ぼすのかについての具体的なデータや事例が不足しています。これにより、近隣を独立したユニットとして捉えることの意義が不明瞭になり、結論の飛躍が生じています。\n\nしたがって、近隣を独立した個々のユニットとして捉えることは、社会的な不平等や犯罪の発生メカニズムを理解するためには不十分であり、より包括的な視点が必要であるという主張には、論理的な欠陥があると言えます。",
"finalConclusion": "**結論:**\n\n本論点に関する肯定派と否定派の主張を分析した結果、以下のような評価が得られました。\n\n1. **肯定派の主張の評価:**\n - 肯定派は、近隣を独立したユニットとして捉えることが、社会的構造の理解において重要であると主張しています。特に、近隣の境界が社会的な不平等や犯罪の発生メカニズムに関連していることを示し、具体的な研究(Sampson et al. 1999; Sharkey 2014)を引用しています。この主張は、論文内の具体的な内容に基づいており、論理的に一貫しています。\n - 最終的な主張でも、近隣の境界が社会的、象徴的、政治的な次元を持つことを再確認し、これが犯罪の機会を生む要因であることを強調しています。これにより、肯定派の主張は一貫性を保ち、論文の内容に基づいています。\n\n2. **否定派の主張の評価:**\n - 否定派は、近隣を独立したユニットとして捉えることが社会的構造の複雑さを過度に単純化する可能性があると指摘しています。特に、近隣の境界が持つ社会的、象徴的、政治的な次元の相互作用を無視することが問題であると述べています。この主張も論理的に一貫しており、論文内の内容に基づいています。\n - ただし、否定派の主張には、具体的なデータや方法論に関する説明が不足している点があり、これが結果の信頼性に疑問を投げかける要因となっています。また、近隣の境界がもたらす影響についての一面的な捉え方が見受けられ、これが主張の説得力を低下させる要因となっています。\n\n3. **ハルシネーションとコンセンサスバイアスのチェック:**\n - 肯定派の主張には、論文内の具体的な引用があり、根拠が明確です。\n - 否定派の主張においても、論文内の内容に基づいており、特にハルシネーションやコンセンサスバイアスの問題は見受けられませんでした。\n\n総じて、肯定派の主張は論文の内容に基づいており、社会的な不平等や犯罪の発生メカニズムを理解するために近隣の境界を考慮することの重要性を強調しています。一方で、否定派はその視点の限界を指摘し、より包括的な視点が必要であると主張しています。両者の主張にはそれぞれの有効な点があり、近隣の社会的境界の特殊性を考慮することは、都市研究において重要な視点であると結論づけられます。"
}
結論だけ取り出すと、「両者の主張にはそれぞれの有効な点があり、近隣の社会的境界の特殊性を考慮することは、都市研究において重要な視点であると結論づけられます。」ということで、この論文の公表を支持する内容が述べられています。
試行3:未公表の論文の査読
本記事冒頭でも述べたように、論文が掲載依頼を申請してから査読されるまでにはかなりの時間を費やします。その非公認の論文を掲載しているサイトから一つの論文
Discriminating models of trait evolution
を使用し、分析にかけました。以下がその議論内容です。
{
"thesis": "本論文は、従来の統計的手法に代わる新しいアプローチとして、判別分析に基づく機械学習手法(EvoDA)を用いて形質進化モデルの識別を行い、特に測定誤差がある実データ条件下でも従来法より高精度で進化モデルの選択が可能であることを示した。",
"affirmativeArgument_R1": "本論文は、従来の統計的手法に代わる新しいアプローチとして、判別分析に基づく機械学習手法(EvoDA)を用いて形質進化モデルの識別を行い、特に測定誤差がある実データ条件下でも従来法より高精度で進化モデルの選択が可能であることを示しています。この主張は、以下の具体的な根拠によって強く支持されます。\n\nまず、EvoDAは、従来のモデル選択手法に比べて、測定誤差に対して高いロバスト性を持つことが示されています。具体的には、EvoDAは、従来のAICに基づくモデル選択と比較して、測定誤差が存在する状況下でも進化モデルの選択精度が向上することが確認されています(引用: \"EvoDA...offering a new avenue for evolutionary inference...with clear improvements in accurately predicting trait models in the presence of measurement error\")。\n\nさらに、EvoDAの性能は、異なる難易度のケーススタディを通じて評価されており、特に複雑な進化モデルの識別においても優れた結果を示しています。例えば、EvoDAは、単純なBMプロセスとより複雑なOUモデルの識別に成功し、さらに複数のモデル間の識別精度を向上させることができることが示されています(引用: \"Case Study II...investigating the predictive performance of EvoDA for discriminating among K = 3 models: BM, OU, and EB\")。\n\nこれらの結果は、EvoDAが進化モデルの選択において、従来の手法に対して明確な利点を持つことを示しており、特に実データにおける測定誤差の影響を考慮した場合において、その有用性が際立っています。したがって、本論文の主張は、EvoDAが形質進化モデルの識別において従来法よりも高精度であることを強く支持するものです。",
"adversarialArgument_R1": "本論文の主張に対する批判は以下の通りです。\n\n1. **測定誤差に対するロバスト性の過大評価**: 論文ではEvoDAが従来のAICに比べて測定誤差に対して高いロバスト性を持つと主張していますが、実際にはEvoDAのアルゴリズムも測定誤差の影響を受けており、特にBMモデルの識別においては低い精度(30-36.2%)を示しています。これは、EvoDAが測定誤差を考慮しているにもかかわらず、BMモデルの識別においては依然として困難があることを示唆しています(引用: \"EvoDA algorithms struggled to classify BM, reflected by low accuracies (30-36.2%)\")。したがって、EvoDAのロバスト性が従来手法に対する明確な利点であるとする主張は、実際のデータにおける性能を考慮すると過大評価であると言えます。\n\n2. **AICの性能に関する誤解**: 論文ではAICが測定誤差に敏感であると述べていますが、AICの性能は条件によって大きく変動し、特にOUモデルにおいては高い精度(99.7%)を達成しています(引用: \"AIC achieved high accuracy for OU (99.7%) but performed poorly for BM (67.0-74.3%)\")。このように、AICは特定の条件下では優れた性能を示すことがあり、EvoDAの優位性を一概に主張することはできません。\n\n3. **モデル選択の難易度の増加に対する対応**: 論文では、候補モデルの数が増えると全ての手法の分類精度が低下すると述べていますが、EvoDAがこの状況においても優れた性能を発揮するという証拠は示されていません(引用: \"Classification accuracy declined across all approaches in these conditions\")。特に、候補モデルが増えるとEvoDAの精度も低下することが示されており、これによりEvoDAの一般化能力に疑問が生じます。\n\n以上の点から、EvoDAの優位性を主張する論文の結論には論理的な飛躍があり、実際のデータに基づく性能評価が不十分であることが問題です。",
"affirmativeArgument_R2": "本論文の主張は、EvoDAが従来の統計的手法に比べて測定誤差に対して高いロバスト性を持ち、進化モデルの選択において優れた性能を発揮することを示しています。以下に、相手の反論に対する再反論を行い、EvoDAの優位性を強く支持する根拠を示します。\n\n1. **測定誤差に対するロバスト性の評価**:\n 相手はEvoDAがBMモデルの識別において低い精度(30-36.2%)を示すことを挙げ、EvoDAのロバスト性を過大評価していると主張しています。しかし、論文ではEvoDAが測定誤差を直接考慮に入れたトレーニングプロセスを採用しており、従来の手法(AICなど)に比べて測定誤差に対して一貫した性能を示すことが確認されています。具体的には、EvoDAは「従来のモデル選択手法が測定誤差に敏感であるのに対し、EvoDAはエラーを考慮しながら決定境界を見つける能力を持つ」と述べられています。この点から、EvoDAのロバスト性は実際のデータ条件下でも有効であることが示されています。\n\n2. **AICの性能に関する誤解**:\n 相手はAICが特定の条件下で高い精度を示すことを指摘していますが、論文ではAICが測定誤差に対して非常に敏感であり、特にBMモデルにおいてはエラー推定なしでは低い精度(67.0-74.3%)を示すことが明記されています。さらに、エラー推定を行った場合、BMモデルの精度は改善されるものの、OUモデルの精度が著しく低下することが示されています。このように、AICは条件によって性能が大きく変動し、EvoDAの一貫した性能と比較すると、AICの信頼性は低いと言えます。\n\n3. **モデル選択の難易度の増加に対する対応**:\n 相手は候補モデルの数が増えると全ての手法の分類精度が低下すると指摘していますが、論文ではEvoDAが複数のモデルを扱う際にも高い精度を維持する能力があることが示されています。具体的には、EvoDAのアルゴリズムは「候補モデルが増えると全ての手法の分類精度が低下するが、EvoDAは他の手法に比べて相対的に高い精度を維持する」と述べられています。このことから、EvoDAはモデル選択の難易度が増す状況でも優れた性能を発揮することが期待されます。\n\n以上のように、EvoDAは測定誤差に対するロバスト性、AICとの比較における一貫した性能、そしてモデル選択の難易度に対する適応能力において、従来の手法に対して明確な優位性を持つことが論文によって示されています。したがって、EvoDAの導入は進化モデルの選択において重要な進展であると強く支持します。",
"adversarialArgument_R2": "本論文におけるEvoDAの主張にはいくつかの論理的な弱点が存在します。以下にその問題点を指摘し、具体的な根拠を示します。\n\n1. **測定誤差に対するロバスト性の過大評価**:\n 論文ではEvoDAが測定誤差に対して高いロバスト性を持つと主張していますが、実際にはEvoDAの精度はBMモデルにおいて30-36.2%と低く、これは測定誤差の影響を受けやすいことを示唆しています。具体的には、EvoDAは「エラーを考慮しながら決定境界を見つける能力を持つ」とされていますが、実際にはその性能は他の手法と比較して一貫して高いわけではなく、特にBMモデルにおいては低い精度が観察されています(文献より)。このため、EvoDAのロバスト性が実際のデータ条件下で有効であるという主張は、データに基づく証拠が不足しています。\n\n2. **AICの性能に関する誤解**:\n 論文ではAICが測定誤差に敏感であると述べていますが、AICの精度は条件によって大きく変動することが示されています。例えば、AICはOUモデルに対して高い精度を示す一方で、BMモデルに対しては67.0-74.3%の精度しか示さず、エラー推定を行った場合にはBMモデルの精度が改善されるものの、OUモデルの精度が著しく低下することが明記されています。このように、AICの性能は条件に依存しており、EvoDAの一貫した性能と比較すると、AICの信頼性は低いとする主張は一面的であり、AICの特定の条件下での性能を無視しています。\n\n3. **モデル選択の難易度の増加に対する対応**:\n 論文ではEvoDAが複数のモデルを扱う際にも高い精度を維持するとされていますが、実際にはEvoDAの精度は候補モデルの数が増えると低下する傾向が見られます。特に、複数のモデルを比較する際には、全ての手法の分類精度が低下することが示されており、EvoDAが他の手法に比べて相対的に高い精度を維持するという主張は、実際のデータに基づく証拠が不足しています。\n\n以上の点から、EvoDAの優位性を支持する主張には論理的な飛躍や方法論の欠陥が見受けられ、実際のデータに基づく証拠が不足しているため、EvoDAの導入が進化モデルの選択において重要な進展であるという結論は再考の余地があります。",
"finalConclusion": "本論文の論点は、判別分析に基づく機械学習手法(EvoDA)が従来の統計的手法に比べて、特に測定誤差がある実データ条件下でも高精度で進化モデルの選択が可能であることを示すことです。\n\n### 肯定派の主張\n1. **EvoDAのロバスト性**: EvoDAは測定誤差に対して高いロバスト性を持ち、従来のAICに比べて進化モデルの選択精度が向上することが確認されている。\n2. **ケーススタディの結果**: EvoDAは複雑な進化モデルの識別においても優れた結果を示しており、特にBMプロセスとOUモデルの識別に成功している。\n3. **実データにおける有用性**: EvoDAは実データにおける測定誤差の影響を考慮した場合に、その有用性が際立つ。\n\n### 否定派の主張\n1. **ロバスト性の過大評価**: EvoDAはBMモデルの識別において低い精度(30-36.2%)を示しており、実際には測定誤差の影響を受けやすい。\n2. **AICの性能の誤解**: AICは特定の条件下で高い精度を示すことがあり、EvoDAの優位性を一概に主張することはできない。\n3. **モデル選択の難易度の増加に対する対応**: 候補モデルの数が増えるとEvoDAの精度も低下することが示されており、EvoDAの一般化能力に疑問が生じる。\n\n### 議論の評価\n- **論理的妥当性**: 肯定派はEvoDAのロバスト性や性能を具体的なケーススタディに基づいて主張しており、一定の説得力があります。しかし、否定派はEvoDAの性能に対する具体的な数値を挙げており、実際のデータに基づく批判を行っています。これにより、否定派の主張は実証的な根拠に基づいており、信頼性が高いと評価できます。\n\n- **ハルシネーションとコンセンサスバイアスのチェック**:\n - 肯定派の主張には、論文内の具体的な引用が示されており、根拠が明確です。\n - 否定派の主張も具体的な数値や条件を挙げており、根拠が示されています。\n - どちらの主張にも、根拠が論文内にあることが確認でき、ハルシネーションやコンセンサスバイアスは見受けられません。\n\n### 結論\nEvoDAは従来の手法に対して一定の利点を持つ可能性があるものの、否定派の指摘するように、特定の条件下での性能やロバスト性に関しては過大評価されている可能性があります。特に、BMモデルの識別における低い精度や、候補モデルの数が増えることによる精度の低下は、EvoDAの一般化能力に疑問を投げかけています。したがって、EvoDAの導入が進化モデルの選択において重要な進展であるという結論には再考の余地があると評価します。"
}
結論だけ取り出すと、「EvoDAの導入が進化モデルの選択において重要な進展であるという結論には再考の余地があると評価します。」ということで、査読の結論としてはこの論文は公表には値しないという結論が下されました。
現状の限界点
プロジェクトを始めたころと比べると、知識汚染やハルシネーションはかなり取り除けた気がしますが、肝心のAIの推論力の限界を感じました。マルチモーダルの難しさ、されどpdfをテキストにする際の情報の欠落などを脇においても、そもそも肯定派エージェントが論文の主張やロジックを十分に追いきれていないせいで論文の公表の後押しを十分にできておらず、結局「よくわからない」が自分の立場を肯定できる否定派エージェントに軍配があがるケースが多くみられました。
「もしかしたら後攻の方が有利なのかも?」と思い肯定派エージェントと否定派エージェントの登場順番を入れ替えても結果は同じでした。
論文投稿支援エディテージのウェブマガジンの投稿によると、有名な学術ジャーナルでは論文のリジェクト率が97%になるものもあり、平均的なジャーナルの査読突破率は50%あたりだそうです。それを加味すると査読ツールの信頼性はそこそこ高いと考えることもできますが、すでに公表されている論文をリジェクトするような内容を出力していることからも、AIの推論力、読解力そしてプロンプトの向上が今後のAI査読ツールの開発には必要不可欠と言えるでしょう。
自分が1からAIやLLMを作ったわけではないので今回はどの論文がすでにデータベースに入っているのかがわからず、やや過剰に知識汚染対策を行いましたが、AIやLLMを1から作った場合はどの論文が学習内容に入っていないのかをコントロールできるため、AI査読ツールの開発には1から作るAIやLLMが適していると感じました。
道半ばでの一区切りとなりましたが、この取り組みで築いた「多視点エージェントによる自動査読基盤」は、次の飛躍への確かな礎です。ここまでのPoCで得られた知見やフレームワークは、次フェーズでの精度向上やUI/UX改善、さらに外部公開へ向けたサービス化に不可欠な宝となります。今回の経験をバネに、今後はより堅牢で使いやすいAI査読プラットフォームを目指して、アカデミア世界の業務効率上昇を願っています。
Discussion