【マサカリ求む】任意の物体にかかる空力特性について何も分からなくなった。しかも理屈はまだ不明。

前回のおさらい

https://zenn.dev/onlinsanity/articles/848fe229c59c59

を見て頂ければ分かるのですが、

• 任意の円柱にかかる抗力の求め方を完全に理解した
• アスペクト比を反映する関数が何故か対数関数だった
• 係数の0.1がどこから来たのかは不明

ってなところです。

極限のお話

上の記事では極限(アスペクト比＝$\infty{}$)を取ってしまうと抗力係数が$\infty{}$に発散してしまう点が問題でした。
そこで、

• 極限が一定の値(今回の場合は1.2)を取りうる
• アスペクト比が0になっても$-\infty{}$に発散しない

このような関数を求めた結果、行きついた先はシグモイド関数でした。

どのシグモイド関数？

シグモイド関数と一言で言っても色々あります。その中でどれが一番適当でしょうか。
条件としては、

• 極限の値が$\infty{}$や$-\infty{}$にぶっ飛ばない関数であること
• 可能な限り簡単な関数であること(パラメータも含め)
• $\frac{1}{\tan{\theta{}}}$をかけても$\infty{}$や$-\infty{}$に発散しない工夫が出来ること

が挙げられます。結論から言ってしまうと、選ばれたのは

$$K\frac{t}{|t|+1};t=ar+b,r=\frac{h}{d},d=\frac{1}{2}\sum{|\varDelta{y}|}より \\ b_D=K(\frac{1}{2}-\frac{1}{|a\frac{h}{d}+b|+1})$$

という関数でした。$\frac{1}{2}$が登場しているのは、$\frac{h}{d}$が0になった時に値をゼロにするためです。
揚力計算のために$\frac{1}{\tan{\theta{}}}$をかけたい場合は、$d=\frac{1}{2}\sum{|\varDelta{y}|}$であることを利用して、

$$\begin{aligned} b_L&=b_D\cdot{}\frac{1}{2d}\sum{|\varDelta{y}|\frac{1}{\tan{\theta{}}}} \\ &=b_D\cdot{}\frac{1}{2d}\sum{\frac{\varDelta{x}|\varDelta{y}|}{\varDelta{y}}} \\ &=b_D\cdot{}\frac{1}{2d}\sum{sgn(\varDelta{y})\varDelta{x}} \end{aligned}$$

とすれば、値は発散しません。
($sgn(\varDelta{y})$は$\varDelta{y}$が正なら1、負なら-1を返す関数です)
いい感じですね。

$K$と$a$と$b$はどうやって決めたの？

Excelでソルバーを使ってホイっと求めました。
$K$はそもそも$r$が$\infty{}$に達したときに頭打ちをさせる値なので1.2固定です。その結果、
$a$はだいたい0.1
$b$はだいたい1
と求まりました。
$a$も$b$もシンプルな値で素晴らしいのですが、この値である理由はさっぱり分かりません。
誰か詳しい人はマサカリを投げてください。

計算式にも着目

さて、そもそもなのですが、以前からすごくナチュラルに$v_a=vp\kappa{}\sin^2{\theta{}}$を使ってきたわけですが、図を描いて、式と見比べたりしてようやくその意味がハッキリしました。
これは$v_a$を二乗して式を整理すると分かるのですが、

$$\begin{aligned} v_a^2&=v^2(p\kappa{})^2\sin^4{\theta{}}より \\ D&=\frac{1}{2}\rho{}v^2(p\kappa{})^2\sum{\frac{\sin^4{\theta{}}\sqrt{\varDelta{x^2}+\varDelta{y^2}}}{d}}+b_D \\ &=\frac{1}{2}\rho{}v^2(p\kappa{})^2\sum{\sin^3{\theta{}}\frac{\varDelta{y}}{d}}+b_D \end{aligned}$$

となり、$\sin^3{\theta{}}$が出てきます。この$\sin^3{\theta{}}$は何を指すのでしょうか。
($b_D$は上のセクションで定義した抗力係数のy切片を表す変数です。)
ここで、風向に対して角$\theta{}$を成す極小平面があったとして話を進めましょう。
まず、この極小平面にとっては、速度$v$は角$\theta{}$を成したことによって速度が相対的に落ち、$v\sin{\theta{}}$となります。
また、この極小平面にかかる圧力も同様に相対的に落ち、$p\sin{\theta{}}$となります。
この時点で、極小平面にかかる動圧は$vp\sin^2{\theta{}}$となるわけです。
この$vp\sin^2{\theta{}}$は極小平面に対して直交するようにかかっている動圧なので、

• 抗力の場合は$v$と平行になる$vp\sin^3{\theta{}}$
• 揚力の場合は$v$と直交する$vp\sin^2{\theta{}}\cos{\theta{}}$

の動圧がかかるわけです。
なので、揚力の場合は上と似たような式で

$$\begin{aligned} v_b^2&=v^2(p\kappa{})^2\sin^2{\theta{}}\cos^2{\theta{}}より \\ L&=\frac{1}{2}\rho{}v^2(p\kappa{})^2\sum{-sgn(\varDelta{x}\varDelta{y})\frac{\sin^2{\theta{}}\cos^2{\theta{}}\sqrt{\varDelta{x^2}+\varDelta{y^2}}}{w}}+b_L \\ &=(\frac{1}{2}\rho{}v^2(p\kappa{})^2\sum{-sgn(\varDelta{x}\varDelta{y})\sin^2{\theta{}}\cos{\theta{}}\frac{\varDelta{x}}{w}})+b_L \end{aligned}$$

という式が導けます。
($b_L$も上のセクションで定義した揚力係数のy切片および正負を決定する変数です。)
(シグマの中で$-sgn(\varDelta{x}\varDelta{y})$をかけているのは、極小平面の成す角度によって揚力が上下に変わってしまうのを表現するためです。)

手を動かしてみる

ソースコードは以下に貼ります。

ソースコード

cylinder4.js

// 定数群
const N = 1000;                                                         // 分割数[個]
const ds = [ 1 / 40, 1 / 10, 1 / 5, 1 / 2, 1, 1, 1, 1, 1 ];             // 円柱の直径[m]
const hs = [ 1, 1, 1, 1, 1, 2, 5, 10, 40 ];                             // 円柱の長さ[m]
const cds = [ 0.98, 0.82, 0.74, 0.68, 0.63, 0.68, 0.74, 0.82, 0.98 ];   // 抗力係数(出典：http://skomo.o.oo7.jp/f28/hp28_63.htm)
const lean = 0.1;                                                       // 抗力係数計算時の傾き(マジックナンバー)
const bias = 1;                                                         // 抗力係数計算時のy切片(マジックナンバー)
const sonic = 340.6520138;                                              // 15℃時の音速[m/s]
const density = 1.225;                                                  // 空気の密度[kg/m^3]
const pressure = 101325;                                                // 1気圧[Pa]
const graphWidth = 720;                                                 // 表示するグラフの横幅[px]
const graphHeight = 480;                                                // 表示するグラフの高さ[px]

// 共通で使う配列
const nar = [ ...Array( N ) ].map( ( k, i ) => i );
const lar = hs.map( ( k, i ) => i );

// 円を描く関数
const cylinder = d => {
    const r = d / 2;
    return ( t ) => {
        return {
            x: r * Math.cos( t ),
            y: r * Math.sin( t )
        };
    };
};

// 円を作る
const foils = lar.map( n => cylinder( ds[ n ] ) );

// 作った円を点にプロット
const xyLists = lar.map( n => nar.reduce( ( p, i ) => {
    const tmp = foils[n]( i * 2 * Math.PI / N );
    p.x.push( tmp.x );
    p.y.push( tmp.y );
    return( p );
}, {
    x: [],
    y: []
} ) );

// 速度のx軸を作る(0～音速まで)
const xSpeedList = nar.map( i => i * sonic / N );

// 従来の式での抗力のリストを作る
const yCDragLists = lar.map( n => nar.map( i => xSpeedList[ i ] ** 2 * density * ds[ n ] * hs[ n ] * cds[ n ] / 2 ) );

// 形状から抗力係数を計算する
const kCd = n => nar.map( i => {
    const tmpX = xyLists[ n ].x[ i ] - xyLists[ n ].x[ i < N - 1 ? i + 1 : 0 ];
    const tmpY = xyLists[ n ].y[ i ] - xyLists[ n ].y[ i < N - 1 ? i + 1 : 0 ];
    const delta = Math.sqrt( tmpY ** 2 + tmpX ** 2 );
    return( ( ( pressure / ( density * sonic ** 2 ) ) ** 2 ) * ( tmpY ** 4 / ( delta ** 3 * ds[ n ] ) ) );
} ).reduce( ( p, c ) => p + c, ( mcd * ( 1 / 2 - 1 / ( lean * ( hs[ n ] / ds[ n ] ) + bias + 1 ) ) ) );
// 速度対樺沢式抗力のリストを作る
const kDrag = ( n, i ) => xSpeedList[ i ] ** 2 * density * ds[ n ] * hs[ n ] * kCd( n ) / 2;
const yKDragLists = lar.map( n => nar.map( i => kDrag( n, i ) ) );

// プロットした速度対抗力を線グラフとして繋ぐ
const sCDrags = lar.map( n => {
    return( {
        x: xSpeedList,
        y: yCDragLists[ n ],
        type: 'scatter',
        mode: 'lines',
        name: 'Conventional(' + hs[ n ] + ':' + ds[ n ] + ')'
    } );
} );
const sKDrags = lar.map( n => {
    return( {
        x: xSpeedList,
        y: yKDragLists[ n ],
        type: 'scatter',
        mode: 'lines',
        name: 'Kabasawa(' + hs[ n ] + ':' + ds[ n ] + ')'
    } );
} );

// 表示するグラフの配列を入れる
const veloDatas = lar.map( n => [ sCDrags[ n ], sKDrags[ n ] ] );

// レイアウト設定
const veloLayouts = lar.map( n => {
    return( {
        height: graphHeight,
        width: graphWidth,
        xaxis: {
            range: [ Math.min( ...xSpeedList ), Math.max( ...xSpeedList ) ],
            title: 'velocity[m/s]'
        },
        yaxis: {
            range: [ Math.min( ...yCDragLists[ n ] ), Math.max( ...yCDragLists[ n ] ) ],
            title: 'aerodynamic drag[N]'
            },
        title: 'Aerodynamic Drag on the Cylinder(' + hs[ n ] + ':' + ds[ n ] + ') vs. Velocity'
    } );
} );

// 実際の描画(velo[n]の名が付いたdivタグの内容として表示)
lar.map( n => Plotly.newPlot( 'velo' + n, veloDatas[ n ], veloLayouts[ n ], {
    editable: true,
    scrollZoom: true,
    showLink: false,
    displaylogo: false,
    modeBarButtonsToRemoie: ['sendDataToCloud']
} ) );

cylinder4.html

<!doctype html>
<html lang="ja">
    <head>
        <script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
    </head>
    <body>
        <div id="velo0"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo1"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo2"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo3"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo4"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo5"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo6"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo7"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo8"><!-- ここに速度対抗力のグラフを表示する --></div>
        <script src="cylinder4.js"></script>
    </body>
</html>

結果発表は前回とほぼ同じなので省略します。ただし前回より精度よく近似出来ていました。

揚力については？

さて、こっちの方がより面倒な問題です。何故なら、

• 揚力を計算する既存の方法が「クッタ・ジューコフスキーの定理」しかない
  • しかもこれは「2次元翼」かつ「完全流体」での話、言わば机上の空論
  • 似たような名前で紛らわしい「クッタ・ジューコフスキーの仮定」を満たさない場合は？
• 翼のアスペクト比と揚力係数の関係が未知

よって、風洞実験を行わないと正確な値は分からない訳です。
なので、ここから先は「ぼくのかんがえたさいきょうのりろん」以上の何物でもありません。
しかしやってみないことには分からないので、適当にジューコフスキー翼を作って検証してみます。
なお、話を簡単にするために対称翼で考えることにします。
また、クッタ・ジューコフスキーの仮定を必ず満たさない翼断面の代表として、
カムテール形状のジューコフスキー翼も作ってみて、それも計算してみます。

待って、カムテールって何？

ドイツのヴニバルト・カム博士という方がいらっしゃったのですが、
その方が従来の涙滴型(ティアドロップ型)流線形の後ろの尖った部分を
スパっと切り落とした形の車を提唱したためにこの名があるそうです。
変に尖った部分を作らなくて良くなるので使い勝手が改善したため人気になったそうです。

さて、実践実践

ソースコードは以下に。

ソースコード

zhukovsky.js

// 定数群
const N = 360;                              // 分割数[個]
const d0 = 0.01;                            // 翼厚のパラメータ
const l0 = 0.35;                            // コード長のパラメータ
const c0 = 0;                               // キャンバー(反り)のパラメータ
const h0 = 1;                               // 翼長[m]
const v0 = ( 100 / 9 );                     // 速度[m/s]
const mcd = 1.2                             // アスペクト比無限大の場合の抗力係数
const lean = 0.1;                           // 抗力/揚力係数計算時の傾き(マジックナンバー)
const bias = 1;                             // 抗力/揚力係数計算時のy切片(マジックナンバー)
const degree = Math.PI / 180 * 180;         // 計測する最大角度[rad]
const sonic = 340.6520138;                  // 15℃時の音速[m/s]
const density = 1.225;                      // 空気の密度[kg/m^3]
const kappa = 1 / ( density * sonic ** 2 ); // 空気の圧縮率[Pa^-1]
const pressure = 101325;                    // 1気圧[Pa]
const graphWidth = 720;                     // 表示するグラフの横幅[px]
const graphHeight = 480;                    // 表示するグラフの高さ[px]

// 共通で使う空配列
const arr = [ ...Array( N ) ].map( ( k, i ) => i );

// radをdegに変換する関数
const rad2deg = r => ( 180 * r / Math.PI );

// 値のプラスかマイナスかだけを返す関数
const sgn = v => v < 0 ? -1 : 1;

// ジューコフスキー変換する関数
const zhukovsky = ( d, l, c ) => {
    const b = l / 4;
    const a = Math.sqrt( ( b - d ) ** 2 + c ** 2 );
    const z = t => {
        return( {
            x: a * Math.cos( t ) + d,
            y: a * Math.sin( t ) + c
        } );
    };
    const invZ = t => {
        const w = ( a * Math.cos( t ) + d ) ** 2 + ( a * Math.sin( t ) + c ) ** 2;
        return( {
            x: ( a * Math.cos( t ) + d ) / w,
            y: -1 * ( a * Math.sin( t ) + c ) / w
        } );
    };
    const zeta = t => {
        const tmp1 = z( t );
        const tmp2 = invZ( t );
        return( {
            x: ( tmp1.x + b ** 2 * tmp2.x ),
            y: ( tmp1.y + b ** 2 * tmp2.y )
        } );
    };
    return( zeta );
};

// ジューコフスキー翼を作る
const foil0 = zhukovsky( d0, l0, c0 );

// 作ったジューコフスキー翼を点にプロット
const xyList = arr.reduce( ( p, i ) => {
    const tmp = foil0( i * 2 * Math.PI / N );
    p.x.push( tmp.x );
    p.y.push( tmp.y );
    return( p );
}, {
    x: [],
    y: []
} );

// アスペクト比を求める
const chord = Math.abs( Math.max( ...xyList.x ) ) + Math.abs( Math.min( ...xyList.x ) );
const thick = Math.abs( Math.max( ...xyList.y ) ) + Math.abs( Math.min( ...xyList.y ) );
const ratio = chord / thick;

// アスペクト比が3を超えていたらカムテール形状にして、原点を描画開始地点とする
const vertex = Math.min( ...xyList.x );
const len = thick * 3;
const orgXList = xyList.x.map( v => v - Math.max( ...xyList.x ) + ( chord / 2 ) );
const trnXList = xyList.x.map( v => ( ( Math.abs( vertex - v ) > len ) ? ( vertex + len ) : v ) + ( len / 2 ) );

// プロットしたジューコフスキー翼を線グラフとして繋ぐ
const trace0 = {
    x: trnXList,
    y: xyList.y,
    type: 'scatter',
    model: 'lines',
    name: 'truncated airfoil'
};
const trace1 = {
    x: orgXList,
    y: xyList.y,
    type: 'scatter',
    model: 'lines',
    name: 'non-truncated airfoil'
}

// 表示するグラフの配列を入れる
const data = [ trace0, trace1 ];

// レイアウト設定
const layout = {
    height: graphHeight,
    width: graphWidth,
    xaxis: {
        range: [ Math.min( ...orgXList ), Math.max( ...orgXList ) ],
        title: ( ratio > 3 ? 'virtual ' : '' ) + 'chord length: ' + chord * 1000 + '[mm]'
    },
    yaxis: {
        range: [ Math.min( ...xyList.y ) * 4, Math.max( ...xyList.y ) * 4 ],
        title: 'max thickness: ' + thick * 1000 + '[mm]'
    },
    title: ( ratio > 3 ? 'Truncated ' : '' ) + 'Zhukovsky Airfoil ( ' + ( ratio > 3 ? 'virtual ' : '' ) + 'aspect ratio: ' + ratio + ' )'
};

// 実際の描画(foilの名が付いたdivタグの内容として表示)
Plotly.newPlot( 'foil', data, layout, {
    editable: true,
    scrollZoom: true,
    showLink: false,
    displaylogo: false,
    modeBarButtonsToRemove: ['sendDataToCloud']
} );

// x軸のリスト化
const rad = i => ( ( i * degree * 2 / N ) - degree );
const xYawList = arr.map( n => rad2deg( rad( n ) ) );

// ヨー角ごとに回転したリストを用意する
const foilYawList = l => arr.map( n => {
    const rotateX = ( x, y ) => Math.cos( rad( n ) ) * x - Math.sin( rad( n ) ) * y;
    const rotateY = ( x, y ) => Math.sin( rad( n ) ) * x + Math.cos( rad( n ) ) * y;
    return arr.reduce( ( p, c ) => {
        p.x.push( rotateX( l[ c ], xyList.y[ c ] ) );
        p.y.push( rotateY( l[ c ], xyList.y[ c ] ) );
        return( p );
    }, {
        x: [],
        y: []
    } );
} );
const foilThickList = l => arr.map( n => Math.max( ...l[ n ].y ) - Math.min( ...l[ n ].y ) );
const foilWidthList = l => arr.map( n => Math.max( ...l[ n ].x ) - Math.min( ...l[ n ].x ) );
// 本来の翼型のリスト
const orgFoils = foilYawList( orgXList );
const orgThicks = foilThickList( orgFoils );
const orgWidths = foilWidthList( orgFoils );
// カムテール形状のリスト
const trnFoils = foilYawList( trnXList );
const trnThicks = foilThickList( trnFoils );
const trnWidths = foilWidthList( trnFoils );

// 樺沢式抗力係数の計算
const bD = t => mcd * ( 1 / 2 - 1 / ( lean * ( h0 / t ) + bias + 1 ) );
const kCd = ( l, t ) => arr.map( n => {
    const tmpX = l.x[ n ] - l.x[ n < N - 1 ? n + 1 : 0 ];
    const tmpY = l.y[ n ] - l.y[ n < N - 1 ? n + 1 : 0 ];
    const delta = Math.sqrt( tmpY ** 2 + tmpX ** 2 );
    return( ( ( pressure * kappa ) ** 2 / t ) * ( tmpY ** 4 / delta ** 3 ) );
} ).reduce( ( p, c ) => p + c, bD( t ) );
// 樺沢式抗力のリストを作る
const kDrag = ( l, t ) => v0 ** 2 * density * t * h0 * kCd( l, t ) / 2;

// 樺沢式抗力をリスト化する
const yVDragList = arr.map( n => kDrag( orgFoils[ n ], orgThicks[ n ] ) );
const yADragList = arr.map( n => kDrag( trnFoils[ n ], trnThicks[ n ] ) );

// プロットした抗力を線グラフとして繋ぐ
const drag0 = {
    x: xYawList,
    y: yADragList,
    type: 'scatter',
    model: 'lines',
    name: 'actual drag'
};
const drag1 = {
    x: xYawList,
    y: yVDragList,
    type: 'scatter',
    model: 'lines',
    name: 'virtual drag'
};

// 樺沢式揚力係数の計算
const kCl = ( l, t, w ) => arr.map( n => {
    const tmpX = l.x[ n ] - l.x[ n < N - 1 ? n + 1 : 0 ];
    const tmpY = l.y[ n ] - l.y[ n < N - 1 ? n + 1 : 0 ];
    const delta = Math.sqrt( tmpY ** 2 + tmpX ** 2 );
    return( ( ( pressure * kappa ) ** 2 / w ) * ( -1 * sgn( tmpX * tmpY ) * ( tmpX * tmpY ) ** 2 / delta ** 3 ) );
} ).reduce( ( p, c ) => p + c, bD( t ) * ( 1 / ( 2 * t ) ) * arr.map( n => {
    const tmpX = l.x[ n ] - l.x[ n < N - 1 ? n + 1 : 0 ];
    const tmpY = l.y[ n ] - l.y[ n < N - 1 ? n + 1 : 0 ];
    return( -1 * sgn( tmpY ) * tmpX );
} ).reduce( ( p, c ) => p + c, 0 ) );
// 樺沢式揚力のリストを作る
const kLift = ( l, t, w ) => v0 ** 2 * density * w * h0 * kCl( l, t, w ) / 2;

// 樺沢式揚力をリスト化する
const yVLiftList = arr.map( n => kLift( orgFoils[ n ], orgThicks[ n ], orgWidths[ n ] ) );
const yALiftList = arr.map( n => kLift( trnFoils[ n ], trnThicks[ n ], trnWidths[ n ] ) );

// プロットした揚力を線グラフとして繋ぐ
const lift0 = {
    x: xYawList,
    y: yALiftList,
    type: 'scatter',
    model: 'lines',
    name: 'actual lift'
};
const lift1 = {
    x: xYawList,
    y: yVLiftList,
    type: 'scatter',
    model: 'lines',
    name: 'virtual lift'
};

// 表示するグラフの配列を入れる
const dragData = [ drag0, drag1, lift0, lift1 ];

// レイアウト設定
const dragLayout = {
    height: graphHeight,
    width: graphWidth,
    xaxis: {
        range: [ rad2deg( -1 * degree ), rad2deg( degree ) ],
        title: 'angles of yaw[deg]'
    },
    yaxis: {
        range: [ Math.min( ...yVLiftList ), Math.max( ...yVDragList ) ],
        title: 'aerodynamic force[N]'
    },
    title: 'Drag and Lift of ' + ( ratio > 3 ? 'Truncated ' : '' ) + 'Zhukovsky Airfoil'
};

// 実際の描画(dragの名が付いたdivタグの内容として表示)
Plotly.newPlot( 'drag', dragData, dragLayout, {
    editable: true,
    scrollZoom: true,
    showLink: false,
    displaylogo: false,
    modeBarButtonsToRemove: ['sendDataToCloud']
} );

// 横風による縦方向にかかる力の計算
const yVLateralList = arr.map( n => yVDragList[ n ] * Math.cos( rad( n ) ) + yVLiftList[ n ] * Math.sin( rad( n ) ) );
const yALateralList = arr.map( n => yADragList[ n ] * Math.cos( rad( n ) ) + yALiftList[ n ] * Math.sin( rad( n ) ) );

// プロットした縦方向の力を線グラフとして繋ぐ
const lateral0 = {
    x: xYawList,
    y: yALateralList,
    type: 'scatter',
    model: 'lines',
    name: 'actual lateral force'
};
const lateral1 = {
    x: xYawList,
    y: yVLateralList,
    type: 'scatter',
    model: 'lines',
    name: 'virtual lateral force'
};

// 表示するグラフの配列を入れる
const lateralData = [ lateral0, lateral1 ];

// レイアウト設定
const lateralLayout = {
    height: graphHeight,
    width: graphWidth,
    xaxis: {
        range: [ rad2deg( -1 * degree ), rad2deg( degree ) ],
        title: 'angles of yaw[deg]'
    },
    yaxis: {
        range: [ Math.min( ...yVLateralList ), Math.max( ...yVLateralList ) ],
        title: 'drag[N]'
    },
    title: 'Lateral Force of ' + ( ratio > 3 ? 'Truncated ' : '' ) + 'Zhukovsky Airfoil ( lower is better )'
};

// 実際の描画(virtの名が付いたdivタグの内容として表示)
Plotly.newPlot( 'late', lateralData, lateralLayout, {
    editable: true,
    scrollZoom: true,
    showLink: false,
    displaylogo: false,
    modeBarButtonsToRemove: ['sendDataToCloud']
} );

// 横風による横方向にかかる力の計算
const yVVerticalList = arr.map( n => yVDragList[ n ] * Math.sin( rad( n ) ) + yVLiftList[ n ] * Math.cos( rad( n ) ) );
const yAVerticalList = arr.map( n => yADragList[ n ] * Math.sin( rad( n ) ) + yALiftList[ n ] * Math.cos( rad( n ) ) );

// プロットした横方向の力を線グラフとして繋ぐ
const vertical0 = {
    x: xYawList,
    y: yAVerticalList,
    type: 'scatter',
    model: 'lines',
    name: 'actual vertical force'
};
const vertical1 = {
    x: xYawList,
    y: yVVerticalList,
    type: 'scatter',
    model: 'lines',
    name: 'virtual vertical force'
};

// 表示するグラフの配列を入れる
const verticalData = [ vertical0, vertical1 ];

// レイアウト設定
const verticalLayout = {
    height: graphHeight,
    width: graphWidth,
    xaxis: {
        range: [ rad2deg( -1 * degree ), rad2deg( degree ) ],
        title: 'angles of yaw[deg]'
    },
    yaxis: {
        range: [ Math.min( ...yVVerticalList ), Math.max( ...yVVerticalList ) ],
        title: 'aerodynamic force[N]'
    },
    title: 'Vertical Force of ' + ( ratio > 3 ? 'Truncated ' : '' ) + 'Zhukovsky Airfoil ( to the right )'
};

// 実際の描画(virtの名が付いたdivタグの内容として表示)
Plotly.newPlot( 'vert', verticalData, verticalLayout, {
    editable: true,
    scrollZoom: true,
    showLink: false,
    displaylogo: false,
    modeBarButtonsToRemove: ['sendDataToCloud']
} );

zhukovsky.html

<!doctype html>
<html lang='ja'>
    <head>
        <script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
    </head>
    <body>
        <div id="foil"><!-- ここに翼型のグラフを表示する --></div>
        <div id="drag"><!-- ここに抗力と揚力のグラフを表示する --></div>
        <div id="late"><!-- ここに仮想抗力(進行方向)のグラフを表示する --></div>
        <div id="vert"><!-- ここに仮想抗力(垂直方向)のグラフを表示する --></div>
        <script src="zhukovsky.js"></script>
    </body>
</html>

＼結果発表～!!／

橙色の方の翼断面のコード長:厚みが6:1ぐらいです。
水色の方はその比率が3:1となるように後端を切り落としたものです。

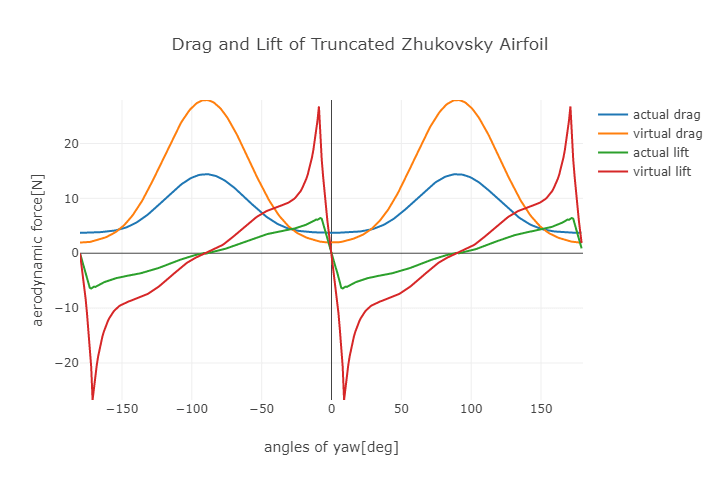
水色(カムテール)と橙色(通常)が抗力(風向に対して必ず同じ方向を向くので常に正)、
緑色(カムテール)と赤色(通常)が揚力(風向に対して正負の向きを取りうる)です。
翼断面は基準となる0°から時計回りに回転しているので、-180～-90°と0～90°は揚力が負となります。
一応、揚力が8～9°辺りでストール(失速)しているのでそれっぽいグラフだとは思います。
思いはするのですが…ストールってこんなに急峻に起こすものでしたっけ？しませんよね？あれ？

上は揚力と抗力の合力が翼と平行な方向に対してどのような感じになっているかを示すグラフです。
正の値ならば抗力、負の値ならば推進力になっているとお考えください。
-90度以下と90度以上は風向が逆転するので合力の向きも反転しています。
だいぶ曲線がぐちゃぐちゃになっている印象です。
と言うか、揚力が推進力になっちゃうこともあるんですね。
某大手自転車メーカーの開発者がインタビューで言っていたことは本当だった…。

今度は揚力と抗力の合力が翼と直交する方向に対してどう力が加わるかを示すグラフです。
これは正の値ならば右、負の値ならば左に力が加わっているとお考えください。(逆かも？)
揚力に引っ張られているフェイズと抗力で押されているフェイズがあることが見て取れます。

一応の考察

まず、結果発表を省略した円柱の抗力についてですが、
シグモイド関数の導入で無限大に対処出来たと言っても過言ではなく、
ついでに図らずもより精度の高い抗力の計算が可能となりました。
また、翼断面については一応グラフの見た目はそれっぽいものが出たので、
今回の導出式は大きく外れてはいないのかな、という印象です。
また、この導出式(特に断面形状による部分)については、現状が微分方程式っぽい状態なので、
適切なパラメータを入れて積分してやれば前方投影長さと下方投影長さを変数とした
もうちょっと扱いやすい式に出来そうな気がしています(絶対出来るとは言っていない)。
また、先にも述べた通り、グラフ上のストールがスパイクしすぎな気がしています。
本当にこのようになるのか、風洞実験のデータと突き合わせてみる必要があります。
だからどなたか自由に使える風洞実験施設を僕に買ってください本当にお願いします。

課題

結局のところ、「計算式にも着目」の項で触れたような後付けの意味付けは出来ても、
真の原理についてはまだまだ不透明で謎が多いのが実情です。
特に、アスペクト比による抗力係数/揚力係数の変化については全く意味不明です。
それっぽい式にそれっぽい関数をぶっつけてそれっぽく値を出しているにすぎません。
そして何よりも、この導出方法は全く風洞実験を経ていない机上の空論でしかないため、
最終的には風洞実験から逃れることは不可能です。いつか必ずぶち当たる壁です。
なので冗談抜きで誰か風洞実験施設を自由に使わせてください本当にお願いします。

まとめ

• 円柱にかかる抗力については、シグモイド関数の導入で精度と理屈上の正しさを向上させることに成功した。
• 任意の断面についての抗力ならびに揚力について、上の方法論をそのまま適用したら「正しそう」な結果が出た。
• 算出方法については、改善すればもう少し単純な計算式に落とし込めると考えられる。
• 算出方法の理屈上の正しさについては全く不明。要調査。

【緩募】マサカリ

もはやミランダルール状態となっている〆ですが、僕は航空力学についてはずぶのド素人です。
故にいい感じのマサカリは超大歓迎です。
航空力学に詳しい諸兄のご意見、ご感想をお待ちしております。