🚲

【マサカリ求む】任意の円柱にかかる空気抵抗を完全に理解した。ただし理屈は不明。

2022/11/24に公開

HTML

前回のおさらい

ここを参照していただければ大体わかるのですが、

直径:高さが1:1でない場合の空気抵抗値を計算出来るかやってみた
直径:高さのアスペクト比が大きくなるにつれて誤差も増えた
何でかはよく分からなかった

ってなところです。

式に潜んでいた致命的間違い

アスペクト比が開くと誤差が開く理由について色々と頭を悩ませていたのですが、
ある時、閃いて計算した結果から抗力係数を逆算してみました。
するとどうでしょう。
アスペクト比が変わっても抗力係数が全く変化していないじゃん。
何という大ポカ。
そもそも、数式を注意深く見れば発見出来た問題だったのです。

\begin{aligned} v_a&=\frac{vp\sin{}^2\theta{}}{\rho{}c^2} \\ &=\frac{vp}{\rho{}c^2}\cdot{}\frac{\varDelta{y^2}}{\varDelta{x^2}+\varDelta{y^2}} \end{aligned}

わざと現実的な計算に使いやすい $\varDelta{x}$ と $\varDelta{y}$ を使った表現に書き換えましたが、
これって図形が等比変形したら $v_a$ が結果的に同じになっちゃいますよね。
道理でアスペクト比が変わっても抗力係数が一緒な訳だ…orz
一応確認はしたのですが、円柱の直径でなく高さを変えてアスペクト比を変化させた場合においても似たような結果が得られました。残念。

音の性質を勘案したら音の性質を勘案しなくて良くなった

何故音の性質を勘案したかは前の前の記事を参照してください。
「お前は何を言っているんだ」と言われかねませんが、上の式で $\rho{}c^2$ が登場していますよね。
ここで $\rho{}$ は流体の密度、 $c$ は流体内での音速です。
さて、 $c$ は一体どのように定義されているのでしょうか。実はニュートン・ラプラスの式で

c=\sqrt{\frac{1}{\rho{}\kappa{}}}

と定義されています。
ここで $\kappa{}$ は流体の圧縮率です。(単位は $Pa^{-1}$ )
これを上の式に代入すると、

v_a=vp\kappa{}\frac{\varDelta{y^2}}{\varDelta{x^2}+\varDelta{y^2}}

となってしまい、音の性質を勘案する必要がなくなったのです。

既知の結果から逆算してみよう

さて、既知の抗力係数とアスペクト比をプロットして、近似した関数を探したところ、厳密には違いましたが大体以下のような関数が得られました。

0.1\cdot{}\ln{(\frac{h}{d})}+0.63

ここで $h$ は円柱の高さ、 $d$ は円柱の直径です。
0.63はアスペクト比が1:1の場合の抗力係数です。
ならば、これを式に組み込めば行けるんと違いますか？
とりあえず手を動かしてみましょう。

いざ実践

ソースコードは以下に載せます。
前回よりは省略できる所を省略したので賢そうなソースになったと思います。
また、上で「圧縮率を使えばいい」と述べたのですが、空気の圧縮率について詳細なデータが手に入らなかったので従来通りの $\rho{}c^2$ を用いた計算を行っています。

ソースコード

cylinder3.js

// 定数群
const N = 1000;                                                         // 分割数[個]
const ds = [ 1 / 40, 1 / 10, 1 / 5, 1 / 2, 1, 1, 1, 1, 1 ];             // 円柱の直径[m]
const hs = [ 1, 1, 1, 1, 1, 2, 5, 10, 40 ];                             // 円柱の長さ[m]
const cds = [ 0.98, 0.82, 0.74, 0.68, 0.63, 0.68, 0.74, 0.82, 0.98 ];   // 抗力係数(出典：http://skomo.o.oo7.jp/f28/hp28_63.htm)
const sonic = 340.6520138;                                              // 15℃時の音速[m/s]
const density = 1.225;                                                  // 空気の密度[kg/m^3]
const pressure = 101325;                                                // 1気圧[Pa]
const graphWidth = 720;                                                 // 表示するグラフの横幅[px]
const graphHeight = 480;                                                // 表示するグラフの高さ[px]

// 共通で使う配列
const nar = [ ...Array( N ) ].map( ( k, i ) => i );
const lar = hs.map( ( k, i ) => i );

// 円を描く関数
const cylinder = d => {
    const r = d / 2;
    return ( t ) => {
        return {
            x: r * Math.cos( t ),
            y: r * Math.sin( t )
        };
    };
};

// 円を作る
const foils = lar.map( n => cylinder( ds[ n ] ) );

// 作った円を点にプロット
const xyLists = lar.map( n => nar.reduce( ( p, i ) => {
    const tmp = foils[n]( i * 2 * Math.PI / N );
    p.x.push( tmp.x );
    p.y.push( tmp.y );
    return( p );
}, {
    x: [],
    y: []
} ) );

// 速度のx軸を作る(0～音速まで)
const xSpeedList = nar.map( i => i * sonic / N );

// 従来の式での抗力のリストを作る
const yCDragLists = lar.map( n => nar.map( i => xSpeedList[ i ] ** 2 * density * ds[ n ] * hs[ n ] * cds[ n ] / 2 ) );

// 形状から抗力係数を計算する
const kCd = ( n ) => nar.map( i => {
    const tmpX = xyLists[ n ].x[ i ] - xyLists[ n ].x[ i < N - 1 ? i + 1 : 0 ];
    const tmpY = xyLists[ n ].y[ i ] - xyLists[ n ].y[ i < N - 1 ? i + 1 : 0 ];
    const delta = Math.sqrt( tmpY ** 2 + tmpX ** 2 );
    return ( pressure / ( density * sonic ** 2 ) ) ** 2 * ( ( tmpY ** 4 ) / ( delta ** 3 * ds[ n ] ) );
} ).reduce( ( p, c ) => p + c, 0.1 * Math.log( hs[ n ] / ds[ n ] ) );
// 速度対樺沢式抗力のリストを作る
const kDrag = ( n, i ) => xSpeedList[ i ] ** 2 * density * ds[ n ] * hs[ n ] * kCd( n ) / 2;
const yKDragLists = lar.map( n => nar.map( i => kDrag( n, i ) ) );

// プロットした速度対抗力を線グラフとして繋ぐ
const sCDrags = lar.map( n => {
    return( {
        x: xSpeedList,
        y: yCDragLists[ n ],
        type: 'scatter',
        mode: 'lines',
        name: 'Conventional(' + hs[ n ] + ':' + ds[ n ] + ')'
    } );
} );
const sKDrags = lar.map( n => {
    return( {
        x: xSpeedList,
        y: yKDragLists[ n ],
        type: 'scatter',
        mode: 'lines',
        name: 'Kabasawa(' + hs[ n ] + ':' + ds[ n ] + ')'
    } );
} );

// 表示するグラフの配列を入れる
const veloDatas = lar.map( n => [ sCDrags[ n ], sKDrags[ n ] ] );

// レイアウト設定
const veloLayouts = lar.map( n => {
    return( {
        height: graphHeight,
        width: graphWidth,
        xaxis: {
            range: [ Math.min( ...xSpeedList ), Math.max( ...xSpeedList ) ],
            title: 'velocity[m/s]'
        },
        yaxis: {
            range: [ Math.min( ...yCDragLists[ n ] ), Math.max( ...yCDragLists[ n ] ) ],
            title: 'aerodynamic drag[N]'
            },
        title: 'Aerodynamic Drag on the Cylinder(' + hs[ n ] + ':' + ds[ n ] + ') vs. Velocity'
    } );
} );

// 実際の描画(velo[n]の名が付いたdivタグの内容として表示)
lar.map( n => Plotly.newPlot( 'velo' + n, veloDatas[ n ], veloLayouts[ n ], {
    editable: true,
    scrollZoom: true,
    showLink: false,
    displaylogo: false,
    modeBarButtonsToRemoie: ['sendDataToCloud']
} ) );

cylinder3.html

<!doctype html>
<html lang="ja">
    <head>
        <script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
    </head>
    <body>
        <div id="velo0"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo1"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo2"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo3"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo4"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo5"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo6"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo7"><!-- ここに速度対抗力のグラフを表示する --></div>
        <div id="velo8"><!-- ここに速度対抗力のグラフを表示する --></div>
        <script src="cylinder3.js"></script>
    </body>
</html>

＼結果発表～!!／

一つずつ結果を見ていきましょう。
まずは高さ:直径が40:1のもの。上が直径、下が高さを変えてあります。
1vs0.025.png

お？
次は高さ:直径が10:1もの。これも上が直径、下が高さを変えてあります。
1vs0.1.png

これは？
次は高さ:直径が5:1のもの。これも(ry
1vs0.2.png

まさか？
次は高さ:直径が2:1のもの。こｒ(ry
1vs0.5.png

来たか？
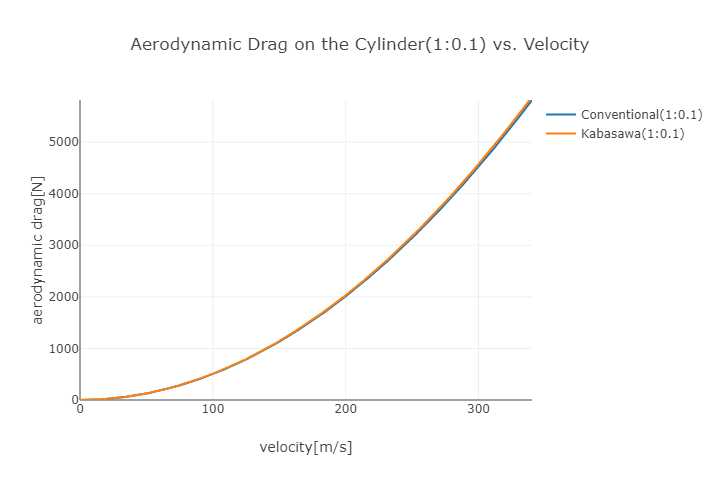
次は高さ:直径が1:1のもの。何度も見せたやつです。

これが一番誤差が大きい気がする…。
結論:無限大が出てこなきゃ大体OK！

考察らしきもの

既知の抗力係数から逆算したとは言え、それっぽく値が出たのは喜ばしいことです。
また、ソースコードの数式をよく読んでいただければ分かると思うのですが、
抗力係数( $C_d$ )の算出が、アスペクト比による部分と、流体の特性による部分と、断面形状による部分とに分かれています。

C_d=0.1\cdot{}\ln{(\frac{h}{d})}+(p\kappa{})^2\cdot{}\sum{}\frac{\varDelta{y^4}}{d\sqrt{\varDelta{x^2}+\varDelta{y^2}}^3} \\

ここで $h$ は円柱の高さ、 $d$ は円柱の直径、 $p$ は流体の圧力、 $\kappa{}$ は流体の圧縮率、 $\varDelta{x}$ は図形のx軸上の微小変化量、 $\varDelta{y}$ は図形のy軸上の微小変化量を指します。
アスペクト比による部分に何故0.1という定数が引っ付いているのかは全く分かりません。
どなたか詳しい方はマサカリをぶん投げてください。お願いいたします。
また、抗力係数が計算出来たということは、実は揚力係数も計算出来ることになります。
何故なら、

抗力と揚力は直交するので、抗力( $D$ )が求まれば揚力( $L$ )は $L=D\frac{\cos{\theta{}}}{\sin{\theta{}}}=D\frac{1}{\tan{\theta{}}}$ で求まるはず( $\theta{}$ は仰角)
抗力と揚力の算出式は、 $\frac{1}{2}v^2\rho{}$ までは共通(最後に前方投影面積 $S$ と抗力係数 $C_d$ の積か下方投影面積 $A$ と揚力係数 $C_l$ の積かをかける)
- なお、 $S$ と $A$ の比は前方投影長さ $d$ と下方投影長さ $w$ の比に等しい

よって、揚力係数( $C_l$ )は導出した抗力係数に $\frac{1}{\tan{\theta{}}}$ をかけるだけでよく、

\frac{1}{\tan{\theta{}}}=\sum{\frac{\varDelta{x}}{\varDelta{y}}}より \\ C_l=0.1\cdot{}\ln{(\frac{h}{w})}\cdot{}\sum{\frac{\varDelta{x}}{\varDelta{y}}}+(p\kappa{})^2\cdot{}\sum{\frac{\varDelta{x^2\varDelta{y^2}}}{w\sqrt{\varDelta{x^2}+\varDelta{y^2}}}}

となります。まだ翼型断面でこの計算式が通用するか分からないので「知らんけど」が付きますが。

課題

円柱が無限大な ~~夢の後の～♪~~ 高さを持っている場合、抗力係数は1.2になるはずなのですが、今回提唱したやり方だと成り立ちません。
また、前述したアスペクト比による部分の説明が出来ない点については調査の続行が必要とされます。
あとは、円柱以外にもこの方法論が通用するかどうかについて、検証が必要です。四角柱とかなら計算出来そうですが、翼型断面の場合は？

まとめ

既知の抗力係数から逆算したところ、アスペクト比の変化を計算上の抗力係数に反映させる方法を発見した。
今回提唱した抗力係数の計算式は、アスペクト比による部分と、流体の特性による部分と、断面形状による部分とに分かれている。
多分、式をちょっと操作すれば揚力も求めることが出来るのではないかと考えられる。
~~誰か僕に風洞実験施設を買ってください。~~

【緩募】マサカリ

恒例となっている〆ですが、僕は航空力学についてはずぶのド素人です。
故にいい感じのマサカリは超大歓迎です。
航空力学に詳しい諸兄のご意見、ご感想をお待ちしております。