Act 14. 線形回帰について学ぶ

はじめに

Act 01. AIで外国為替を自動売買するまでの道のりをベースに学習を進めて行く。

前回は機械学習の概念について学習した。
今回は機械学習のアルゴリズム（人間でいう脳みそのようなもの？）について学習する。
※アルゴリズムとは・・・問題を解決したり目標を達成したりするための手順や計算方法、処理方法

学習はChatGTPさん考案の以下の順序で進めて行く。

学習順序

教師あり学習

1. 線形回帰: 基本的な回帰問題を学ぶ。
2. ロジスティック回帰: 分類問題の基本を理解する。
3. 決定木: シンプルで直感的なモデル。
4. ランダムフォレスト: 決定木のアンサンブル学習。

教師なし学習

1. k平均法: クラスタリングの基本。
2. 主成分分析（PCA）: 次元削減の手法。

強化学習

1. 基本的な概念: エージェント、環境、報酬の関係を理解する。
2. Q学習: 簡単な強化学習アルゴリズム。
   ※強化学習は重要だと判断したため、概念から再度学習する。

線形回帰

まず、ChatGTPさんに線形回帰について詳しく教えてと命令してみた。
すると以下の回答を貰った。

線形回帰分析は、最も基本的かつ広く用いられている回帰手法の一つで、目的変数（従属変数）と説明変数（独立変数）との関係をモデル化するために使用されます。以下に、線形回帰の基本的な概念、手法、評価指標、実装方法について詳しく説明します。

1. 基本概念

   線形回帰は、次のような線形関係を前提とします。

   $$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n + \epsilon$$
   • $y$: 目的変数（予測したい値）
   • $x_1, x_2, \ldots, x_n$: 説明変数
   • $\beta_0$: 切片（yの値が0のときの定数項）
   • $\beta_1, \beta_2, \ldots, \beta_n$: 各説明変数の係数（影響の大きさ）
   • $\epsilon$: 誤差項（予測と実際の値の差）

2. モデルの適合

   モデルをデータに適合させるために、最小二乗法が一般的に使用されます。これは、誤差項の二乗和を最小化することで、係数（$beta$）を求める方法です。具体的には、次の目的関数を最小化します。

   $$\text{SSE} = \sum_{i=1}^{m} (y_i - \hat{y}_i)^2$$
   • $m$: データポイントの数
   • $y_i$: 実際の値
   • $\hat{y}_i$: 予測された値

3. 仮定条件

   線形回帰にはいくつかの仮定があります：

   • 線形性: 目的変数と説明変数との関係が線形である。
   • 独立性: 説明変数が互いに独立である。
   • 同分散性: 誤差項の分散が一定である（ホモスケダスティシティ）。
   • 正規性: 誤差項が正規分布に従う。

4. 評価指標

   モデルの性能を評価するための一般的な指標は以下です。

   • 決定係数 (R²): 目的変数の分散のうち、どれだけがモデルによって説明されているかを示します。1に近いほど良いモデルです。
   • 平均二乗誤差 (MSE): 予測値と実際の値の二乗誤差の平均。値が小さいほど良いモデル。
   • 平均絶対誤差 (MAE): 絶対誤差の平均。解釈が容易で、外れ値の影響を受けにくい。

5. 実装方法

   Pythonのライブラリを使用して線形回帰を実装する方法を示します。一般的には、scikit-learnライブラリが用いられます。

   import numpy as np
   import pandas as pd
   from sklearn.model_selection import train_test_split
   from sklearn.linear_model import LinearRegression
   from sklearn.metrics import mean_squared_error, r2_score
   
   # データの読み込み
   data = pd.read_csv('data.csv')  # 自分のデータに置き換えてください
   X = data[['feature1', 'feature2']]  # 説明変数
   y = data['target']  # 目的変数
   
   # データの分割
   X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
   
   # モデルの作成
   model = LinearRegression()
   model.fit(X_train, y_train)
   
   # 予測
   y_pred = model.predict(X_test)
   
   # 評価
   mse = mean_squared_error(y_test, y_pred)
   r2 = r2_score(y_test, y_pred)
   
   print(f'Mean Squared Error: {mse}')
   print(f'R²: {r2}')
   

   うーん。全くわからん！
   ということで、線形回帰について色々調べてみようと思う。

そもそも線形回帰とは？

線形回帰については【機械学習】線形回帰（前編）| 線形回帰の理論が分かりやすかった。
動画が消えた時ようにメモを残しておく。

線形回帰とは簡単に言うと、与えられた入力データに基づいて、出力（ターゲット）を予測するための分析手法のこと。

簡単だけど身長と体重に関する以下のようなデータがあったとする。
このような直線が求められた状態であれば、170cmという入力データを与えることで、出力を予測することが出来る。

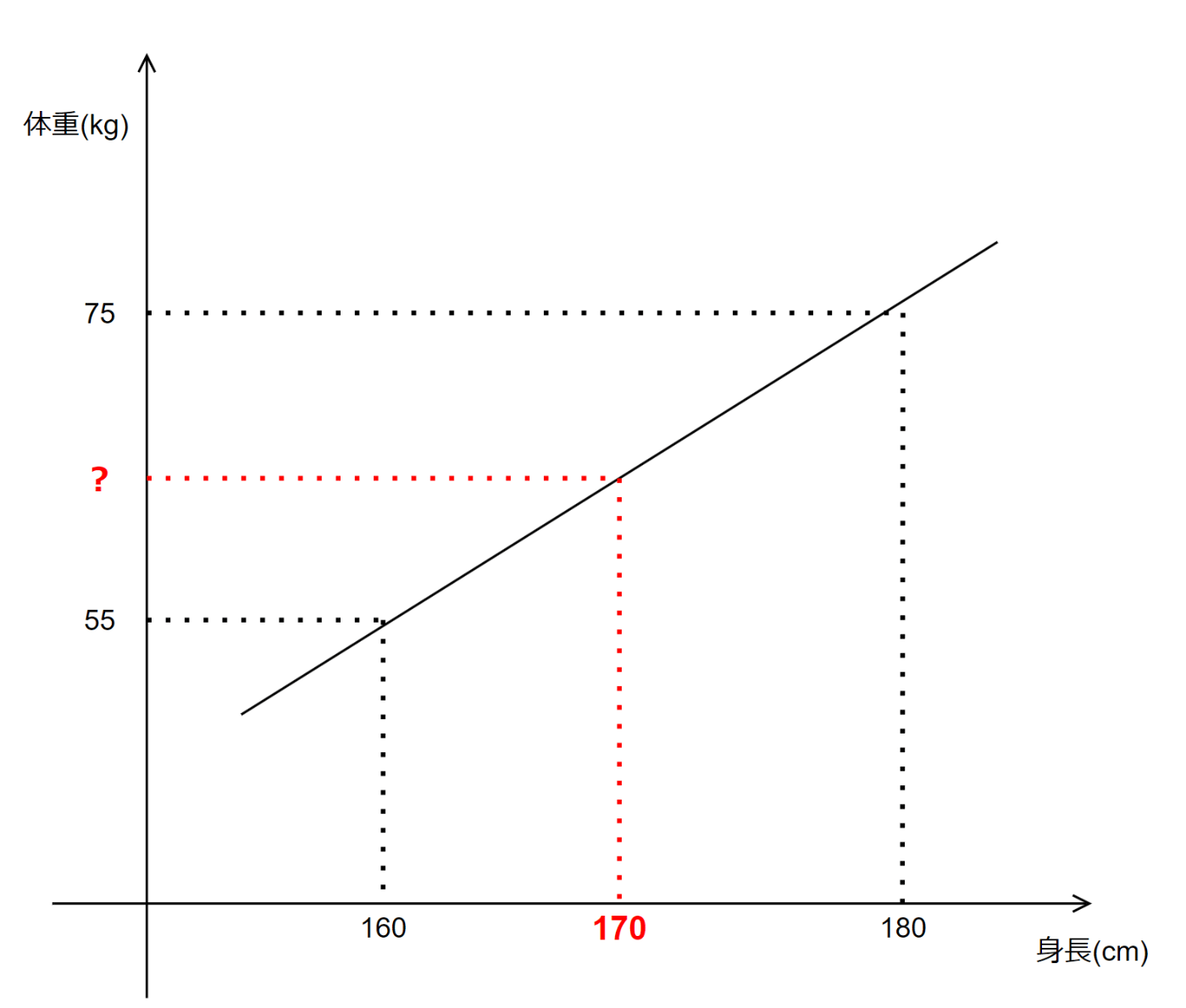
なるほどなるほど、これが線形回帰ね。イメージは沸く。
ではどうやってこの直線を求めているのか。

以下のようなデータがあったとする。

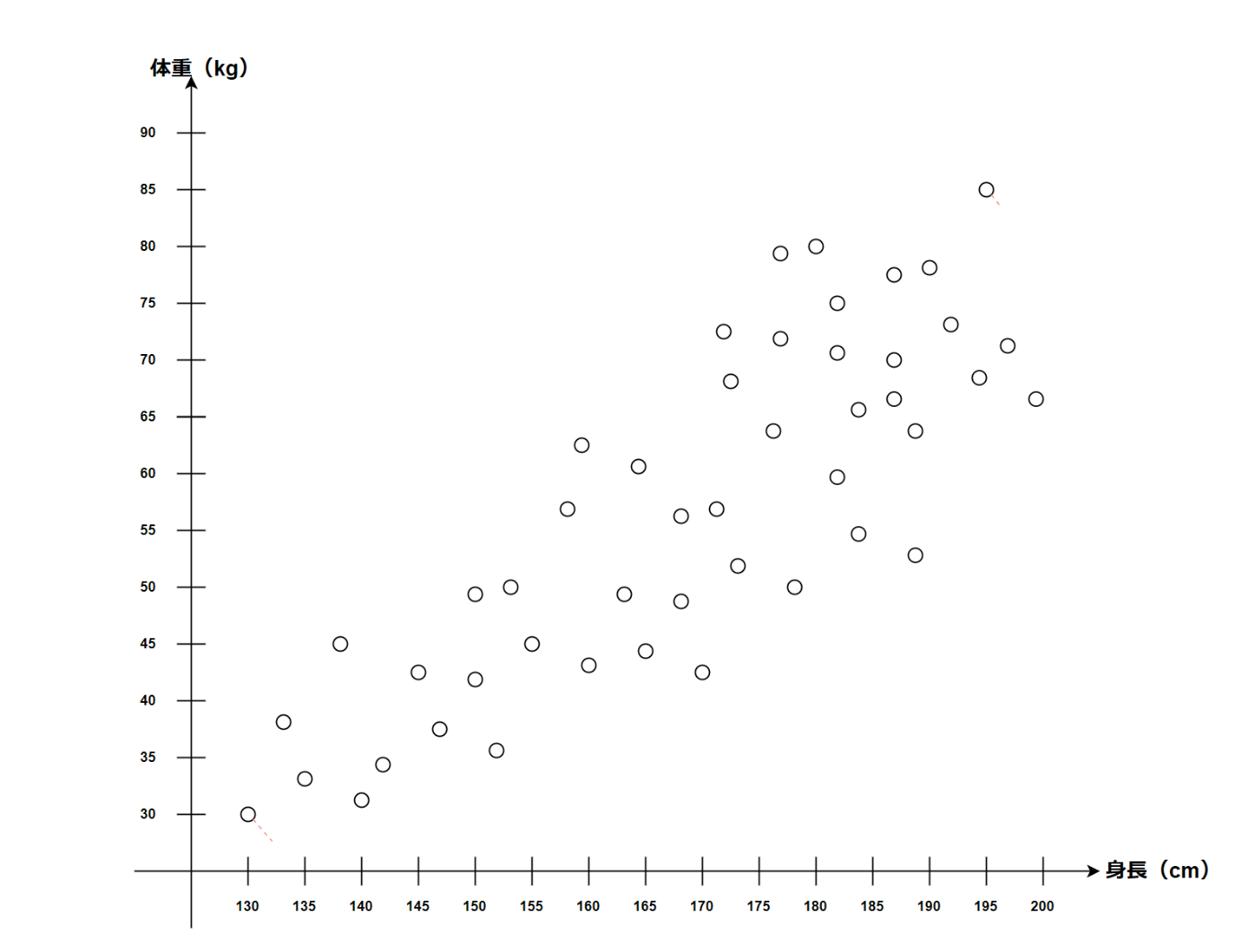
我々人間は一目見ただけで以下のような線が思い浮かぶと思う。
これは今までの経験上（つまり教師あり学習済みであるため）このような判断ができる。

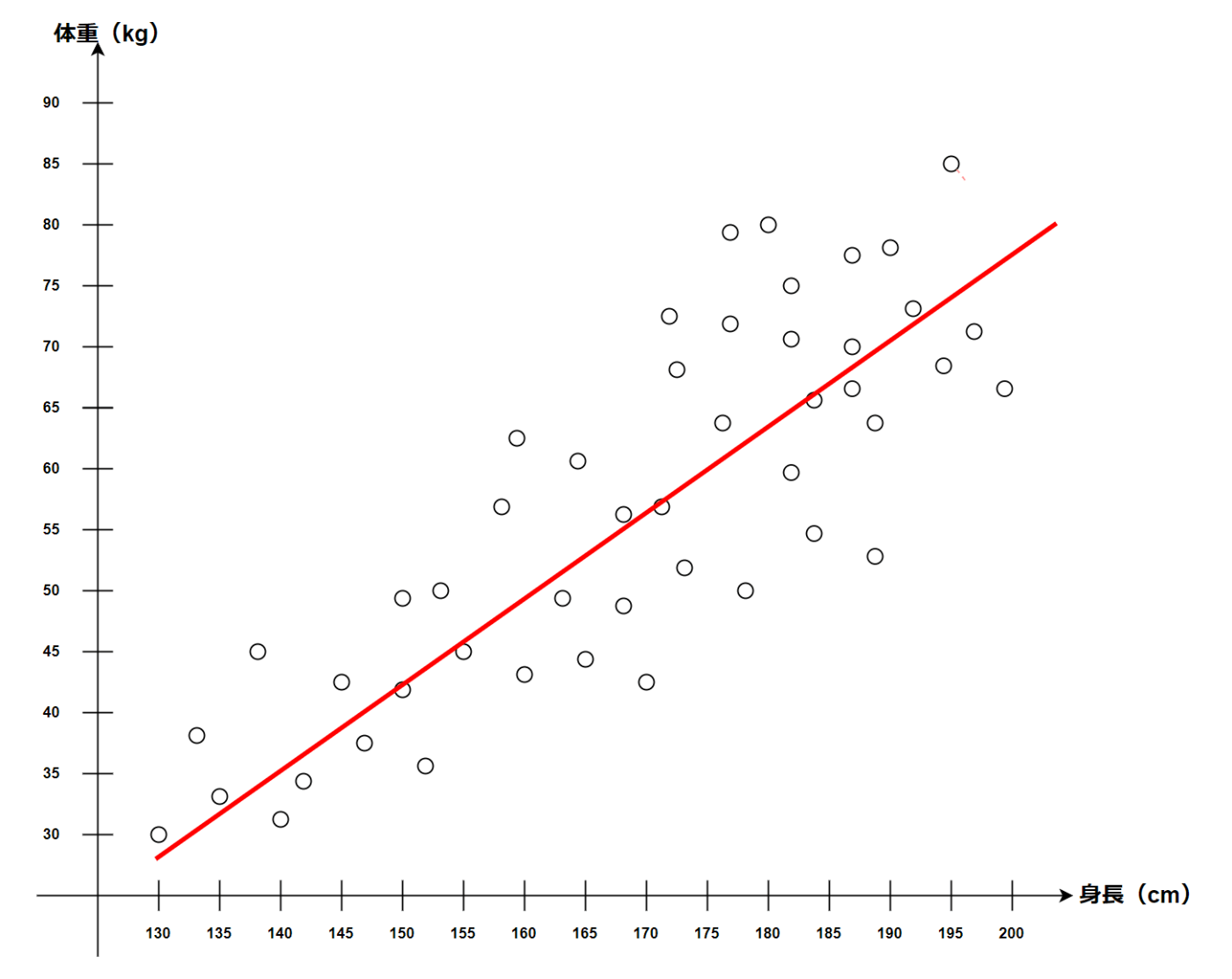
３歳の子供に線を引いてといったらこのような線を引く可能性もある。

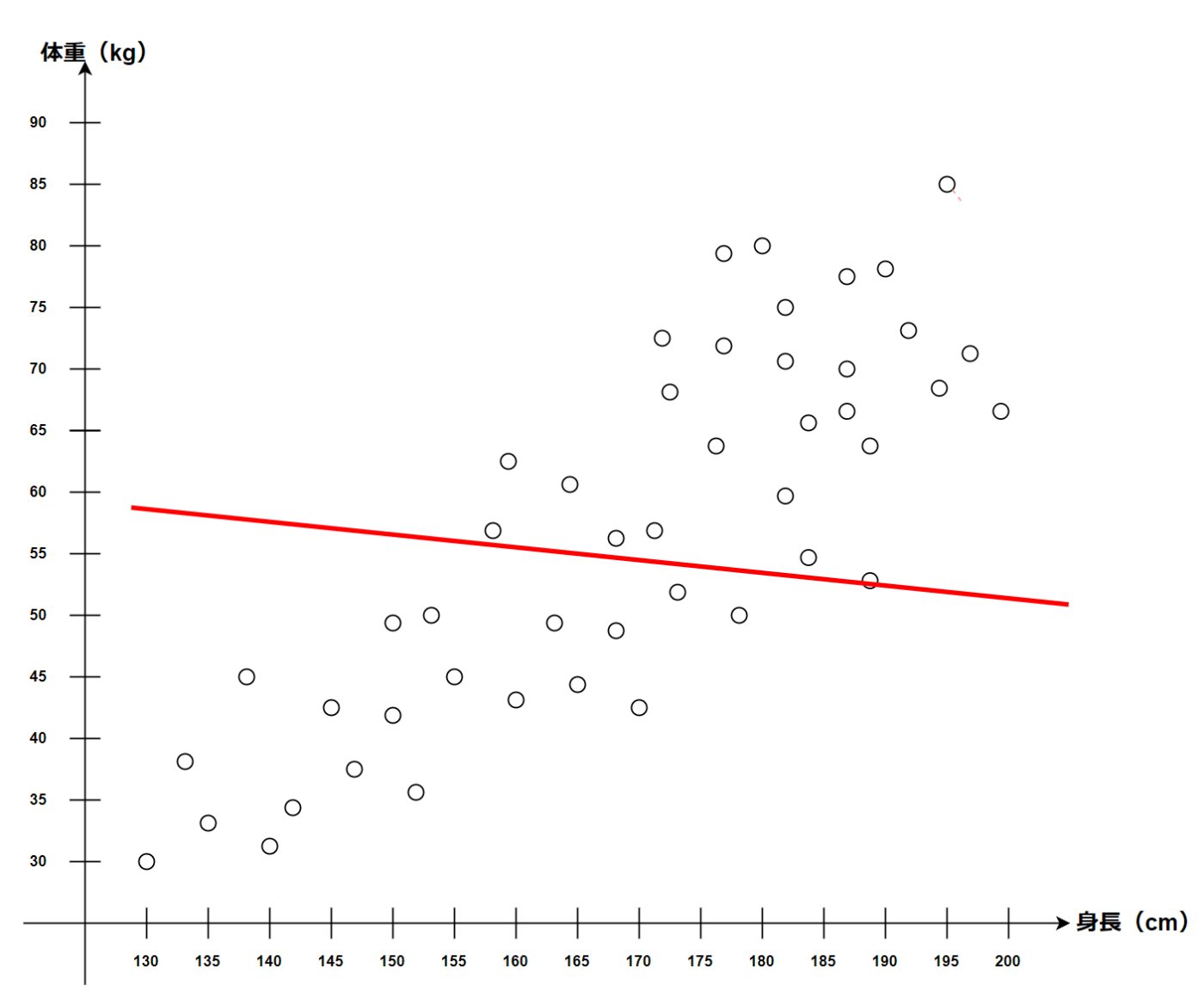
AIも子供と同じく学習前なのでどこに線を引けばよいか分からない。
そんな時に正解の線を求めるために使う手法が最小二乗法！

最小二乗法について

ということで最小二乗法について。
最小二乗法とは簡単に言うと、データと予測の差をできるだけ小さくする方法。
具体的には、予測した値と実際の値の差（誤差）を小さくするように直線を引く方法。

途中を省略しているが以下のようなイメージ。
それぞれのデータと予測の誤差が小さい直線が引けている。

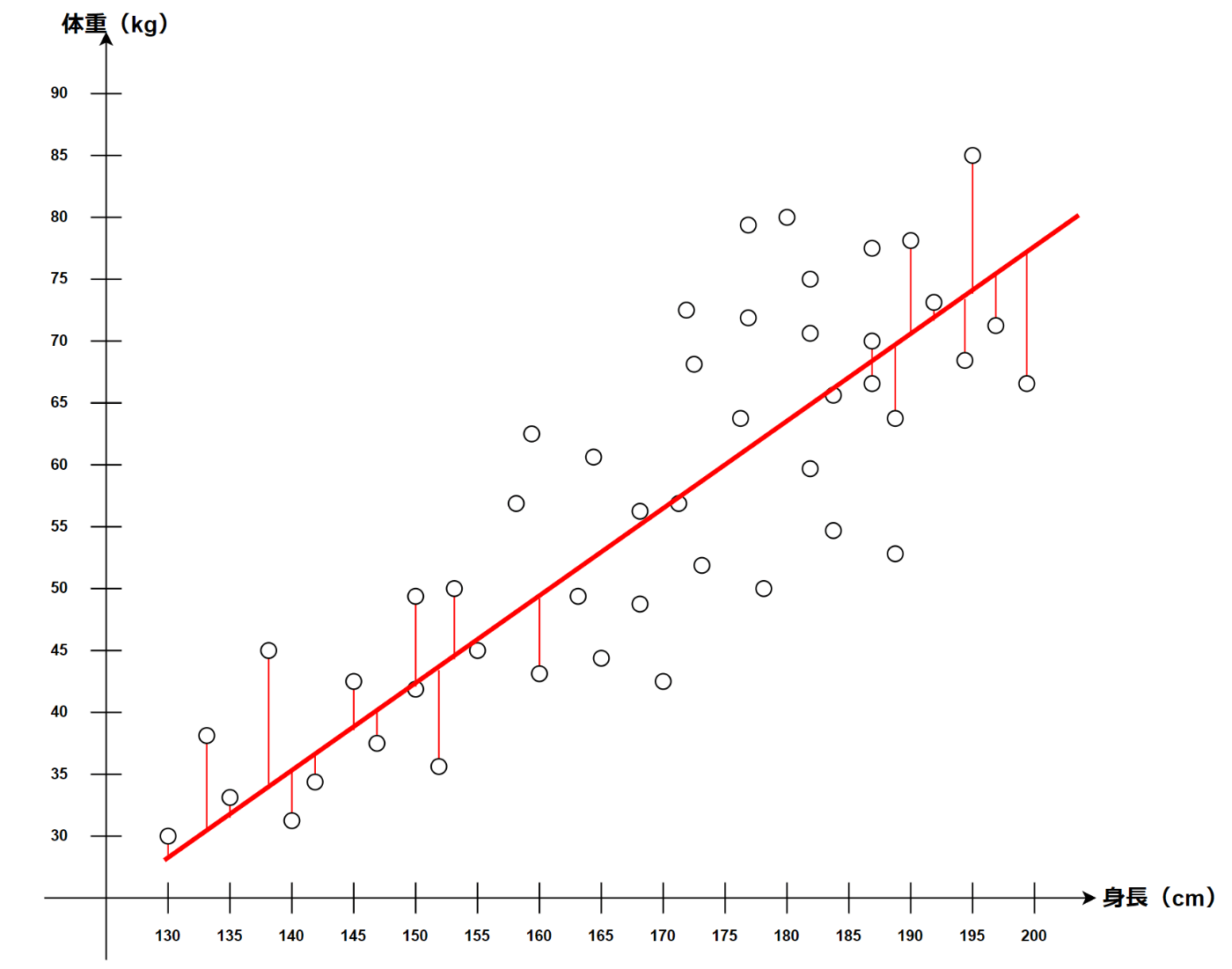
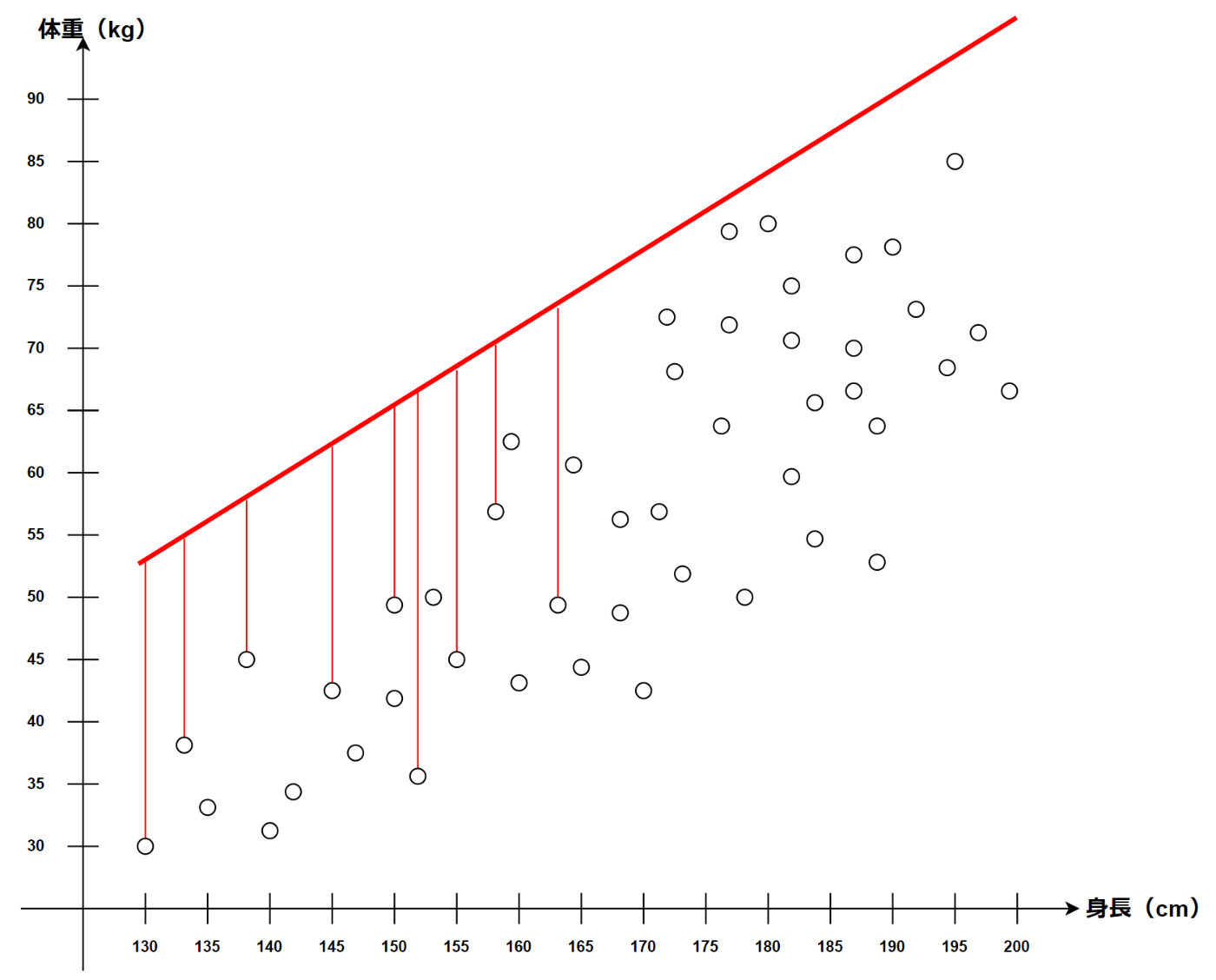
誤差の大きい直線は以下のようなイメージ。
明らかに適切な直線ではないことが分かる。

一つ疑問、なぜ最小二乗法なのか。最小法ではだめなのか？

一部抜粋してみたが、以下のようにデータと予測の誤差はプラスもしくはマイナスとなる。
この時、最小法にしてしまうと正と負の値が相殺しあうため、正確な予測値を求めることが出来ない。

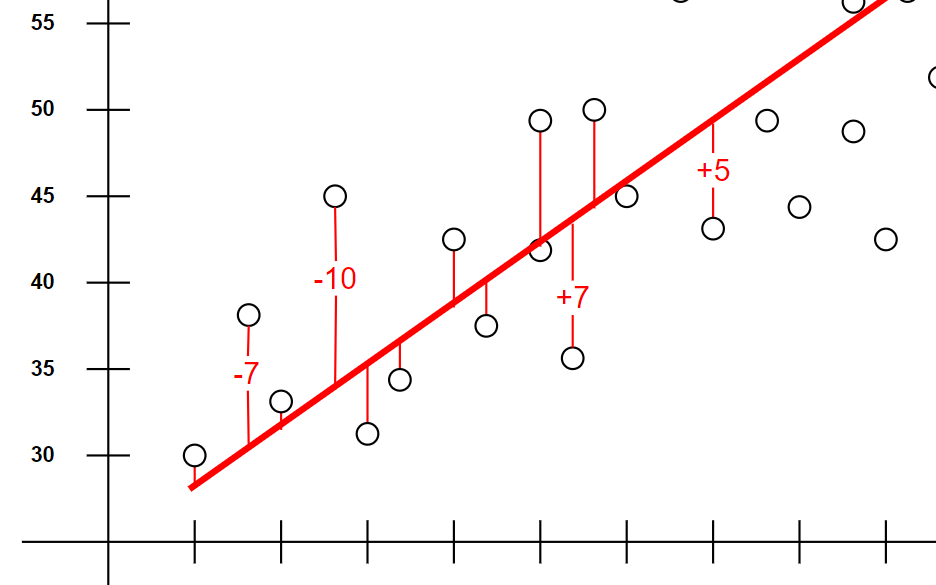
例えば以下のような直線を引いた場合でも誤差は+5となってしまう。
これは良くないよね。

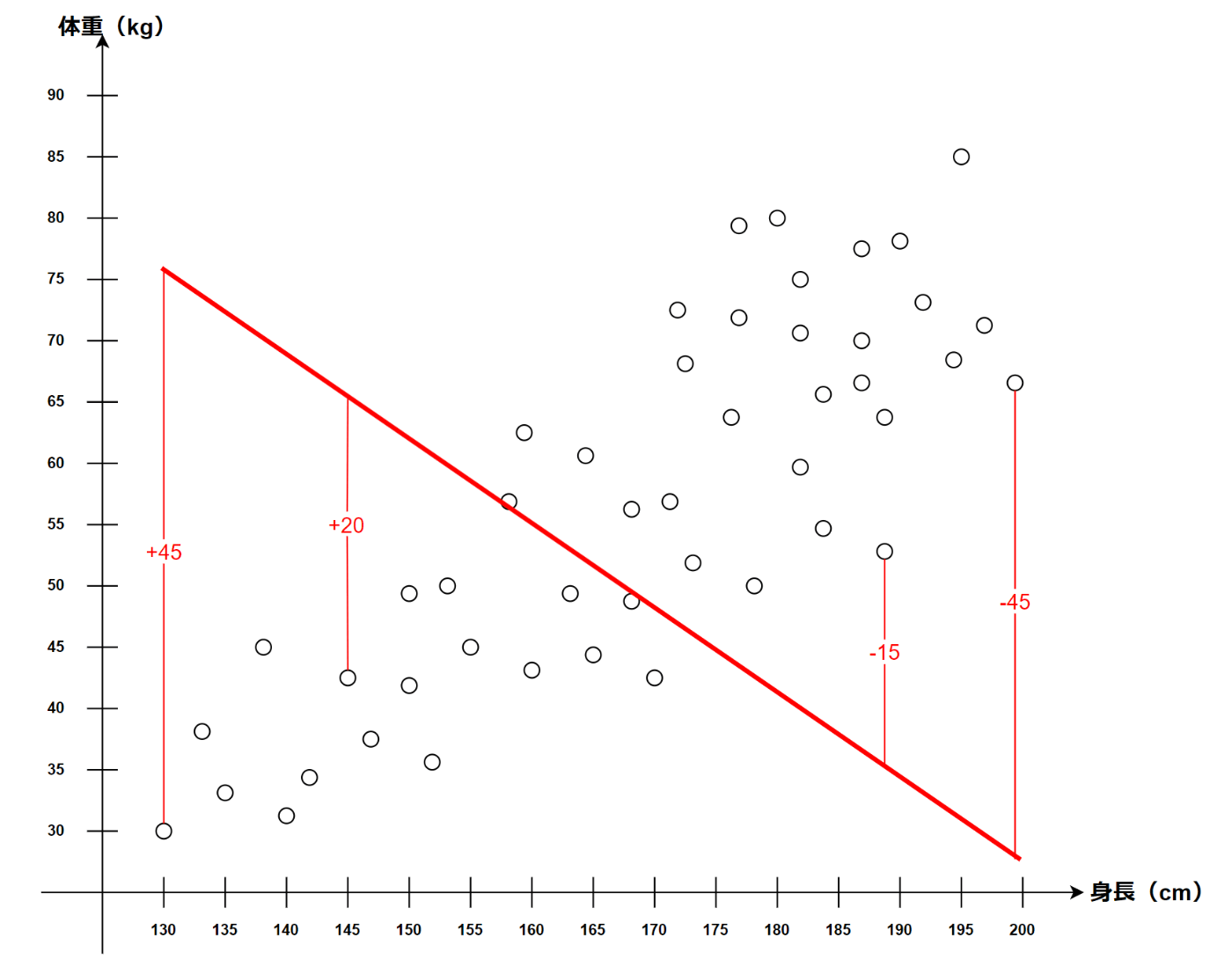
ということで、すべての値を二乗してその総和を求め、それを最小にすることで最適な直線を求めよう！という風に理解をした。

ここで一つ疑問。
絶対値ではだめなのか？ということ。

別にダメではないが、計算が面倒になるため最小二乗法を用いるのが基本らしい。
線形回帰分析を行うために、最小二乗法を用いて最適な直線を引くということは分かった。
これで完璧！と思いきやそうではない。

どうやって最小と判断するのか。という疑問が上がると思う。
最小を求めることは分かったが、果たして今現在のそれが最小の値なのか。どこで最小と判断するのか。それはまだわからない。

そこで使用するのが勾配降下法！

勾配降下法

勾配降下法については【機械学習】単回帰と勾配降下法（前編）【大学数学】が分かりやすかった。

以前学んだ微分も使うことで傾きを求めていき、傾きが０になった個所が最小になる。
なるほどなるほど。

勾配降下法についての図を描こうと思ったが、結構面倒なので割愛する。
この動画が消されないことを祈るしかない…。

さいごに

これで線形回帰分析に方法についてなんとなく理解できた！
ただ…、原理は理解したけど数式は全然理解できていないし、今回は単純な直線だったが曲線の場合もあるのでは？など色々考えるともっと勉強しないとダメそう。

色々課題は残っているのかもしれないが、いったん重要そうな内容は理解できたため次に進もうと思う。

ここで完璧を求めて横道にそれてしまうと、目的を見失いかねないし、どこかで躓き挫折する可能性の方が高い。

次はpythonを使って線形回帰分析を行う記事を作ろうかな。

ではまた