Act 23. k平均法について学ぶ

はじめに

Act 01. AIで外国為替を自動売買するまでの道のりをベースに学習を進めて行く。

前回までは教師あり学習のアルゴリズムについて勉強してきた。
4つのアルゴリズムを学習して、ある程度は理解できたため、今回から教師なし学習について学習していく。

今後学習する内容は以下の通り。
学習はChatGTPさん考案の以下の順序で進めて行く。

教師なし学習のトップバッターはk平均法とやら。
どんなものかは分からないが、どうせ平均値を取ってなんかするんだろ！という印象。

学習順序

教師あり学習

1. 線形回帰: 基本的な回帰問題を学ぶ。　2024/11/13 学習済み
2. ロジスティック回帰: 分類問題の基本を理解する。 2024/11/17 学習済み
3. 決定木: シンプルで直感的なモデル。 2024/11/20 学習済み
4. ランダムフォレスト: 決定木のアンサンブル学習。 2024/11/22 学習済み

教師なし学習

1. k平均法: クラスタリングの基本。
2. 主成分分析（PCA）: 次元削減の手法。

強化学習

1. 基本的な概念: エージェント、環境、報酬の関係を理解する。
2. Q学習: 簡単な強化学習アルゴリズム。
   ※強化学習は重要だと判断したため、概念から再度学習する。

k平均法

ChatGTPさんの回答

いつもの通りChatGTPさんにどんなアルゴリズムなのか教えてもらう。

余談だが、最近ChatGTPのサブスクを契約したため、なんだかいい感じに勉強が進んでいる気がする。
予測の精度は上がったような気がするけど、そもそも未知の領域の勉強をしているため精度が上がっているのかは分からない（笑）

以下はChatGTPさんの回答。

k平均法（k-means）について

k平均法は、教師なし学習のクラスタリング手法の一つで、データをk個のクラスタ（グループ）に分割するアルゴリズムです。データがどのようなパターンで分布しているかを把握する際に役立ちます。

k平均法の仕組み

1. 初期化
   クラスタ数 $k$ を事前に決定し、データ空間内にk個の初期重心（クラスタ中心） をランダムに配置します。

2. 割り当て（Assignment）
   各データポイントを、最も近いクラスタの中心（重心）に割り当てます。

   • 距離は通常、ユークリッド距離（直線距離）を用います。

   • クラスタ $C_i$ に属するデータポイント $x_j$ の条件は次の通り：

     $$C_i = \{x_j \mid \|x_j - \mu_i\|^2 \leq \|x_j - \mu_k\|^2, \, \forall k \neq i\}$$

     ここで、$\mu_i$ はクラスタ $C_i$ の重心。

3. 重心の更新（Update）
   各クラスタに属するデータポイントの平均を計算し、その値を新たな重心とします。

   $$\mu_i = \frac{1}{|C_i|} \sum_{x_j \in C_i} x_j$$

4. 収束条件の確認
   データポイントの割り当てや重心の位置が変化しなくなる、もしくは一定の繰り返し回数に達するまで、2～3のプロセスを繰り返します。

k平均法の具体例

データポイントが以下のように2次元平面に配置されていると仮定します：

$$(1, 2), (1, 4), (1, 0), (10, 2), (10, 4), (10, 0)$$

クラスタ数 $k = 2$（2つのクラスタ）で実行します。

1. 初期重心をランダムに選択：
   $(1, 2)$ と $(10, 2)$

2. データの割り当て：
   各データポイントを、近い重心に割り当てます。例えば、$(1, 4)$ は重心 $(1, 2)$ に近いのでクラスタ1に割り当てます。

3. 重心の更新：
   各クラスタの平均を計算して、新しい重心を更新します。

4. 繰り返し：
   割り当てと更新を収束するまで繰り返します。

メリットとデメリット

メリット

• 実装が簡単で計算コストが比較的低い。
• 収束が速い（通常は数十回の反復で収束）。

デメリット

• $k$ の値を事前に決める必要がある。
• 初期の重心の選び方に依存し、結果が異なる場合がある。
• 球状で均等に分布しているデータには適しているが、複雑な形状には不向き。
• 外れ値の影響を受けやすい。

応用例

1. マーケティング
   顧客を購入履歴に基づいてグループ化し、ターゲットを絞ったキャンペーンを実施。

2. 画像圧縮
   画像のピクセルをk個の色にクラスタリングして、色数を減らす。

3. 異常検知
   正常データをクラスタリングし、外れたデータを異常と見なす。

理解が深まるよう、他に必要な補足があればお知らせください！

とのこと。
いやー、久しぶりに意味わからないのが来たぞー！
何か、∀ガンダムでしか見たことがない記号もあるし。

脱線するけど、スパロボの∀ガンダムって結構強かったよね？
ちなみにスパロボの敵だと、エヴァ関連と阿修羅男爵が苦手だった。味方だとナデシコも嫌だったね。分かる人いる…？

自分なりに解説

ChatGTPさんの説明を自分なりに理解するために色々調べたので、それを記事に書いていこうと思う。

そもそも教師なし学習とは

久しぶりに教師なし学習に振れたため、もう一度おさらいした方が良いと思った。
教師あり学習では、入力と出力の両方を用いて学習を行わせることで、予測値と実際の値の誤差を最小にしていくアルゴリズムや、分類を行うアルゴリズムなどを学習してきた。

教師なし学習は、出力が存在せず入力のみで学習を行うアルゴリズムのことを指す。
そのため、与えられたデータから意味を見い出す（データの構造やパターンなど）ものだった。

教師なし学習にはいくつか種類があるが、このシリーズではクラスタリングと次元削減について学習する。

• クラスタリング: データを似ているもの同士でグループ化する
  参考：教師なし学習（クラスタリング） | ノートで伝える機械学習入門シリーズ
• 次元削減: 高次元のデータに対して、情報をなるべく失わずに低次元に圧縮する
  参考：教師なし学習（主成分分析） | ノートで伝える機械学習入門シリーズ

今回学習するk平均法はクラスタリングの手法の一つ。

k平均法

ということでお待ちかねのk平均法について。
お待ちかねと言いつつ先ほど参考として載せた教師なし学習（クラスタリング） | ノートで伝える機械学習入門シリーズの内容がk平均法になっている。

つまりここで自分が説明することはあまりない…。
なのでChatGTPさんの回答について解説していこうと思う。

1. 初期化

クラスタ数 $k$ を事前に決定して、データ空間内に $k$個の初期重心をランダムに配置する。
これに関しては動画で出ている内容そのまま。

ちなみに、クラスタ数 $k$ は、我々人間が決定するパラメータ（つまりハイパーパラメータ）になる。

2. 割り当て（Assignment）

次に各データポイントを、最も近いクラスタの中心（重心）に割り当てる。
これに関しても動画で出ている内容そのまま。

問題はこの後の割り当てる方法だよね。

距離は通常、ユークリッド距離（直線距離）を用いる。

こちらに関しては、「空間内の2点間の直線距離を算出して近いものを割り当てるよー」ということで理解した。

クラスタ $C_i$ に属するデータポイント $x_j$ の条件は次の通り。

$$C_i = \{x_j \mid \|x_j - \mu_i\|^2 \leq \|x_j - \mu_k\|^2, \, \forall k \neq i\} >$$

ここで、$\mu_i$ はクラスタ $C_i$ の重心。

問題はこっち。お前は意味が分からない！
まず $C_i$ とは何なのか。そこから説明していく。

例えば以下のようなデータあり、そのデータに対してクラスタリングを行うとする。
$k = 2$ として、$2$つのクラスタを作るように指定する。

$2$つのクラスタを作るため、ランダムな位置に初期重心が配置される。
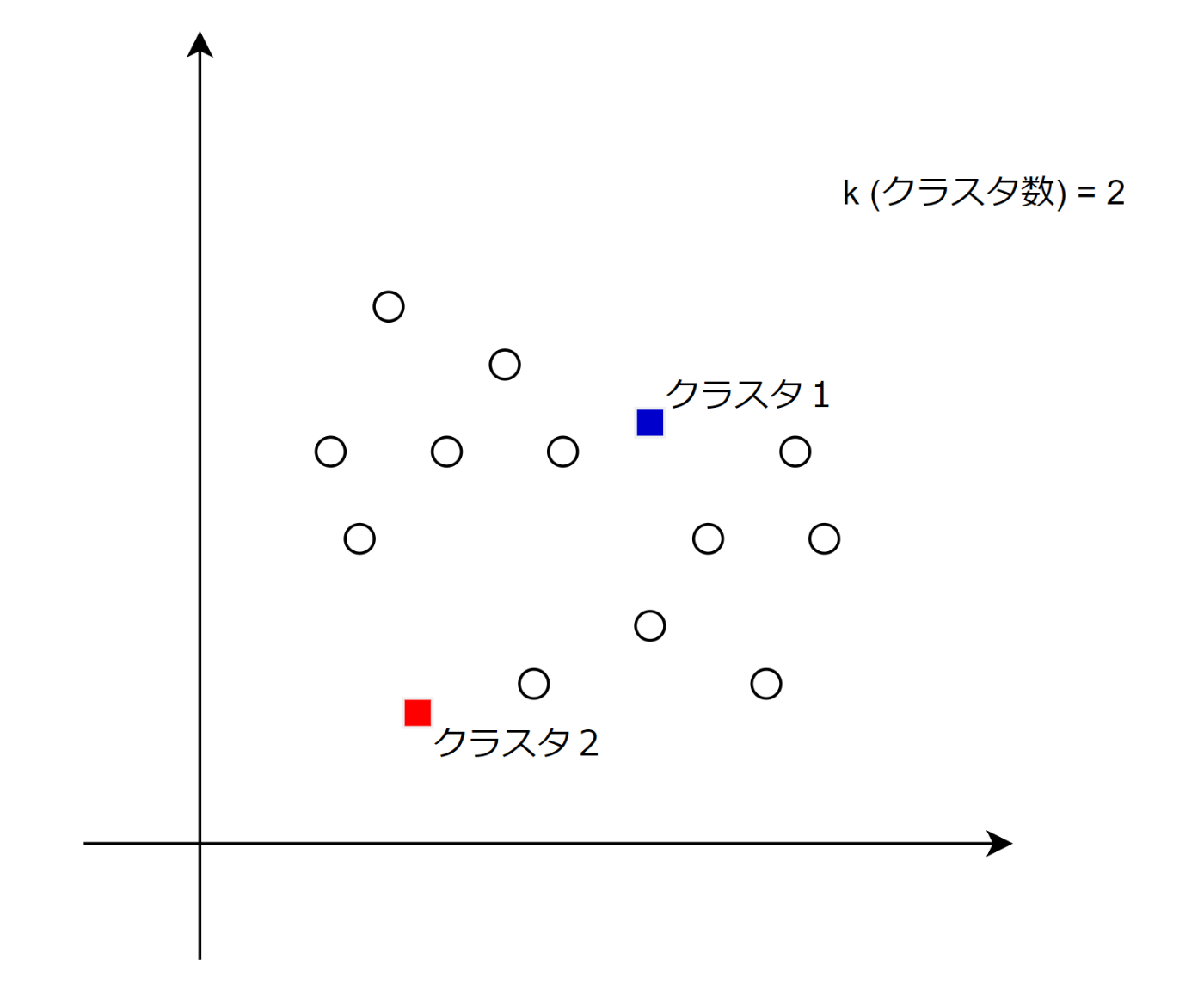
そしてユークリッド距離で最も近いクラスタに割り当てられる。

この時、完成したクラスタを $C_1$ や $C_2$ と呼ぶという感じで理解した！
つまり $C_i$ とは何個目のクラスタなのか、ということ。

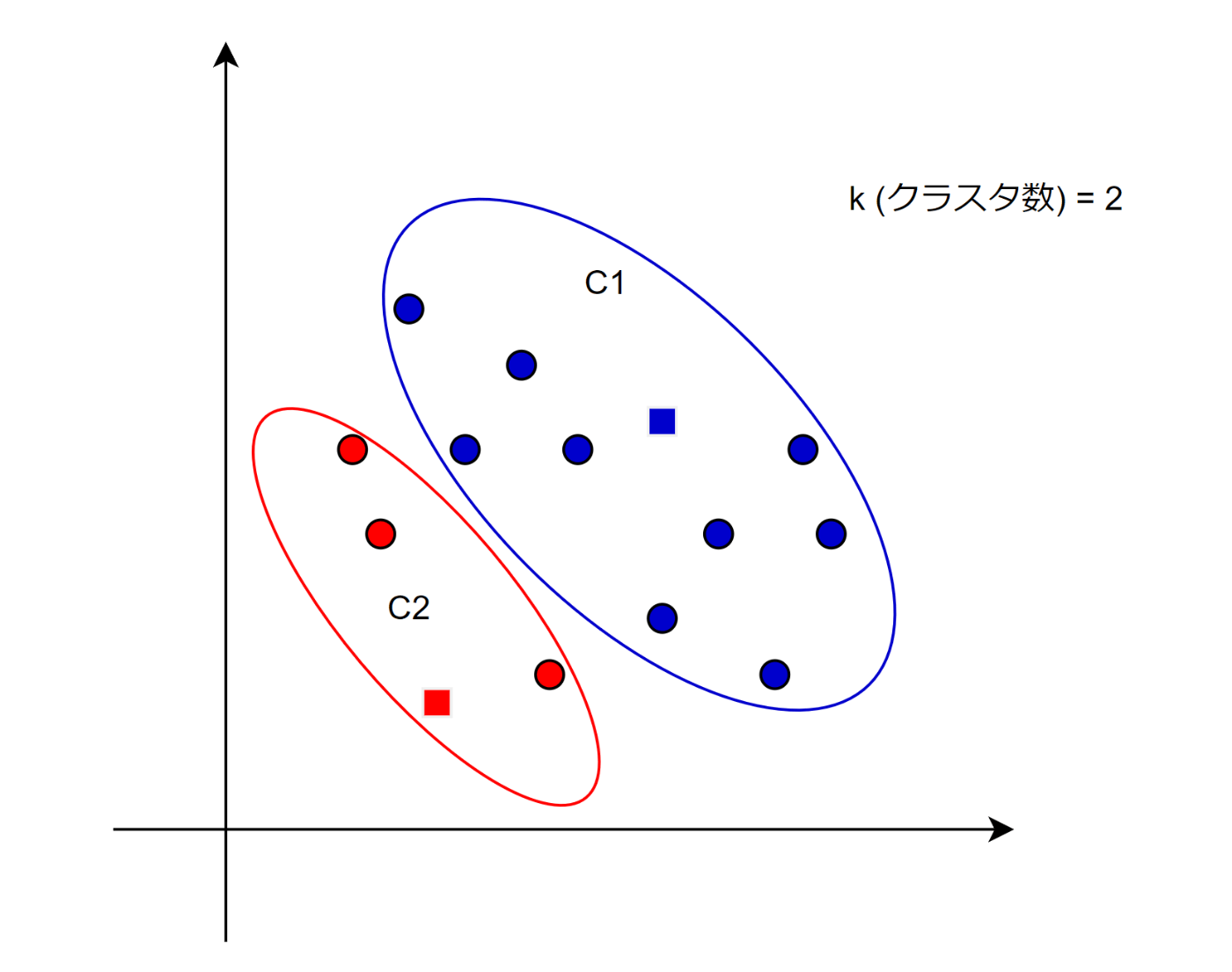
そしてここからが問題。
これの意味を紐解いていく必要がある…。

$$C_i = \{x_j \mid \|x_j - \mu_i\|^2 \leq \|x_j - \mu_k\|^2, \, \forall k \neq i\}$$

この数式は、各データポイントを最も近いクラスタ中心（重心）に割り当てることを目的としている。
そのための計算ということを頭の片隅に置いて読んでほしい。

まずは簡単なやつから。

• $x_j$: データポイントの一つを指す
• $\mu_i$: クラスタ$i$の重心、つまり、$C_i$の重心という意味のはず
• $\mid$: 数学の集合記法における「条件」を示すもの

意味不明ポイント①
これって何ですか？

$$\|x_j - \mu_i\|^2$$

結論としては、「ベクトルの長さ（距離）」を表す記号。
では具体的にどんな計算をするのかって話だよね。

ここに関しては調べていてすぐに分かった。
例えば以下のような2点間の距離を求めたかったとする。
$x_j = (2, 3)$ で $\mu_i = (5, 7)$

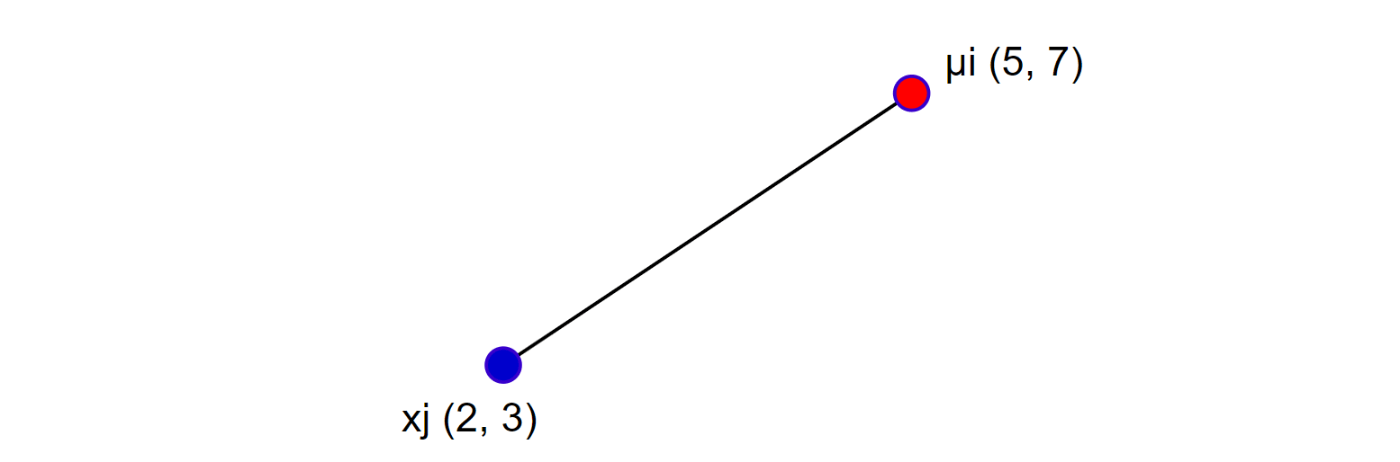
その場合はこうすればいけるはずだ。
2点間の辺$a$を求める場合は、三平方の定理$(a^2 = b^2 + c^2)$で行けた。

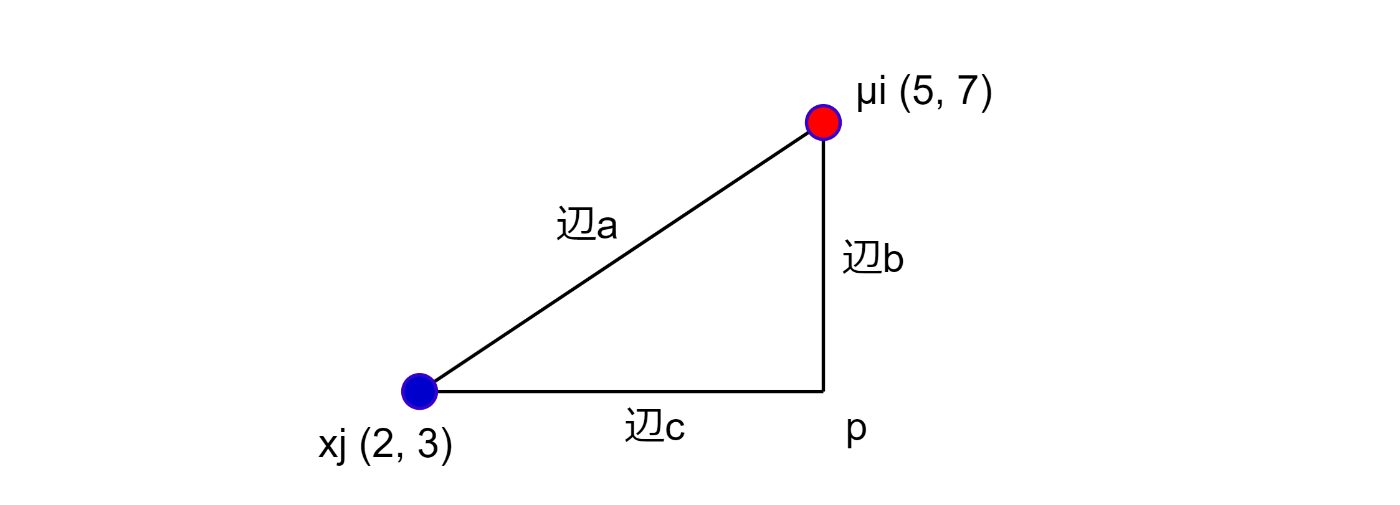
つまり以下の様になる。

$$a^2 = 3^2 + 4^2 = 9 + 16 = 25$$

ということで $\|x_j - \mu_i\|^2 = 25$ だね。（実際はこんなに簡単な式じゃないが…。）

改めて、$\|x_j - \mu_i\|^2$はベクトルの長さ（距離） を表すもの。

意味不明ポイント②
これって何ですか？

$$\forall k \neq i\$$

• $\forall$
  まずはこれから。
  これは「すべて」という意味の数学記号らしい。つまり∀ガンダムは全てのガンダム…？の生みの親的な…？

• $k \neq i$
  これは $k$ は $i$ ではないみたいな意味。

つまり「$i$ 以外の全ての $k$ に対して」のような意味。

さて、役者は揃った！

$$C_i = \{x_j \mid \|x_j - \mu_i\|^2 \leq \|x_j - \mu_k\|^2, \, \forall k \neq i\}$$

こいつは、すべての他のクラスタ重心と比べて、このクラスタ重心が一番近い場合に$x_j$を$C_i$に含めるという意味だ！
きっとあっているはず！

かなり長くなったが、それぞれのデータポイントをクラスタに割り当てる流れは理解できた。

3. 重心の更新（Update）

続いては重心の更新について。

クラスタを作ることができたら、その集合の中で重心を決めなおす。
例えば以下のようなイメージ。

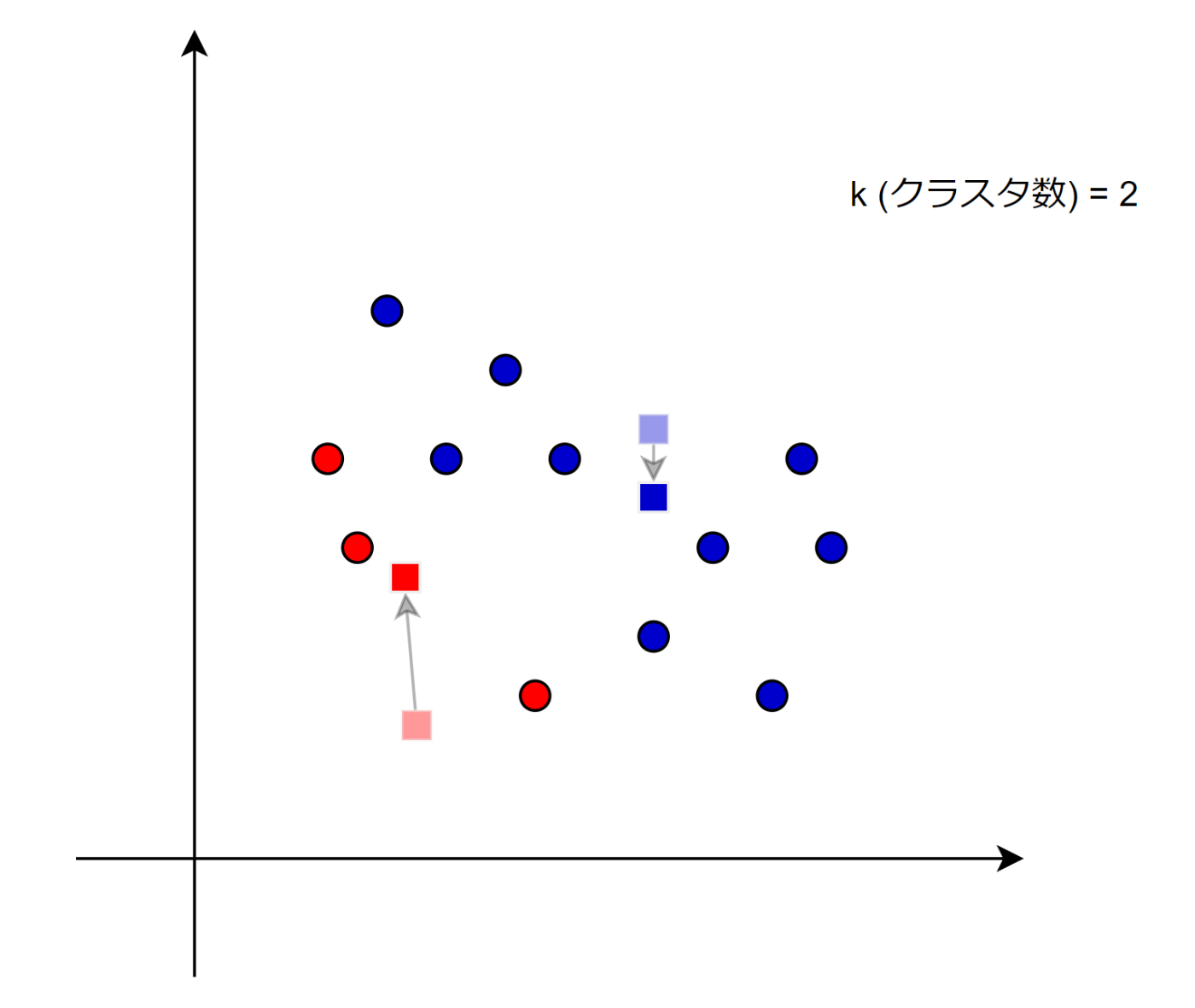
重心を求める式は以下の通りだった。

$$\mu_i = \frac{1}{|C_i|} \sum_{x_j \in C_i} x_j$$

また新しい記号が…。
ただ、先ほどの内容に比べると簡単。

これは、クラスタ $i$ の 重心（中心点） である $\mu_i$ を計算するための式。
重心はクラスタに属するすべてのデータポイントの「平均」を取ることで求められる。

• $\mu_i$
  $\mu_i$ は、クラスタ $i$ の重心（中心点）を表す。

• $|C_i|$
  $|C_i|$ は、クラスタ $i$ に属するデータポイントの「数（個数）」を表す。
  例えば、クラスタ $C_i$ にデータポイントが3つあれば、$|C_i| = 3$ となる。

• $\sum_{x_j \in C_i} x_j$
  「$\sum_{x_j \in C_i}$」は、「クラスタ $C_i$ に属するすべてのデータポイント $x_j$ を足し合わせる」という意味らしい。

• $\frac{1}{|C_i|}$
  これは、データポイントの数（$|C_i|$）で合計を割ることで、平均値を計算している。

クラスタ $C_i$ に属するすべてのデータポイントの座標を合計し、データポイントの個数で割ったものが重心 $\mu_i$ になるってことだ…。

4. 収束条件の確認

後は２～３を繰り返して行い重心の位置をずらしていく。
そして、変化が起きなくなったら学習を中断するという流れ。

さいごに

いやー、難しかった。
新しい記号とか出てくると発狂しそうになる…。

10代のころからもっと勉強しておけば良かった…と後悔したが、人生で一番若いのは今だから、とにかく今頑張るぞ！

次は python でクラスタリングをやってみる。
教師なし学習は初めてだからどんな感じでやるのか楽しみ。

ではまた。