Act 20. Pythonで決定木を試す

はじめに

Act 01. AIで外国為替を自動売買するまでの道のりをベースに学習を進めて行く。

前回は決定木の概要について学習した。
なので今回は実際にpythonで決定木を使った分析を行う。

データセットが必要になるため、pythonで提供されているアヤメという花のデータセット？を使用する。

決定木

結論

まずはコードを見たい方に。

Act20.py

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
import matplotlib.pyplot as plt

# データセットの読み込み
iris = load_iris()
X = iris.data  # 特徴量
y = iris.target  # ラベル

# データセットをトレーニングセットとテストセットに分割（8:2の割合）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 決定木モデルの作成
clf = DecisionTreeClassifier(random_state=42)

# モデルの学習
clf.fit(X_train, y_train)

# テストデータを使って予測
y_pred = clf.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

# 分類レポートの表示
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

# 決定木の可視化
plt.figure(figsize=(24, 16))  # 図のサイズを指定
plot_tree(
    clf,  # 学習済みの決定木モデル
    feature_names=iris.feature_names,  # 特徴量の名前
    class_names=iris.target_names,  # クラスの名前
    filled=True,  # ノードを色付け
    rounded=True,  # ノードの角を丸くする
    fontsize=10  # フォントサイズ
)
plt.title("Decision Tree Visualization")  # タイトル
plt.show()

出力も載せておく。
ロジスティック回帰の時と同様に100%の正解率となっている。

Accuracy: 1.00

Classification Report:
              precision    recall  f1-score   support

           0       1.00      1.00      1.00        10
           1       1.00      1.00      1.00         9
           2       1.00      1.00      1.00        11

    accuracy                           1.00        30
   macro avg       1.00      1.00      1.00        30
weighted avg       1.00      1.00      1.00        30

plot_treeの結果は以下の通り。
決定木の分類条件まで見れるなんて凄すぎる…。

コードの説明

いきなり全て書いてしまったからコードの説明をしていく。

データセット

データセットに関してはAct 17. Pythonでロジスティック回帰を試すと同じだから、この記事を参照して欲しい。

モデルの構築

ここら辺も毎度おなじみの流れとなっている。

Act20.py

from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split

# データセットの読み込み
iris = load_iris()
X = iris.data  # 特徴量
y = iris.target  # ラベル

# データセットをトレーニングセットとテストセットに分割（8:2の割合）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 決定木モデルの作成
clf = DecisionTreeClassifier(random_state=42)

# モデルの学習
clf.fit(X_train, y_train)

決定木の場合はDecisionTreeClassifierというクラスを使用する。
日本語だと"決定木"ってダサいのに英語にするとかっこいいじゃんか。

予測とモデルの評価

学習したモデルに対して予測とモデルの評価を行う。

Act20.py

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report

# データセットの読み込み
iris = load_iris()
X = iris.data  # 特徴量
y = iris.target  # ラベル

# データセットをトレーニングセットとテストセットに分割（8:2の割合）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 決定木モデルの作成
clf = DecisionTreeClassifier(random_state=42)

# モデルの学習
clf.fit(X_train, y_train)

# テストデータを使って予測
y_pred = clf.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

# 分類レポートの表示
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

ロジスティック回帰でも出現したaccuracy_scoreとclassification_reportを使用する。
こちらの説明についてもロジスティック回帰の記事を読んでほしい。

決定木のプロット

ここからが本題みたいなところはある。

Act20.py

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

# データセットの読み込み
iris = load_iris()
X = iris.data  # 特徴量
y = iris.target  # ラベル

# データセットをトレーニングセットとテストセットに分割（8:2の割合）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 決定木モデルの作成
clf = DecisionTreeClassifier(random_state=42)

# モデルの学習
clf.fit(X_train, y_train)

# テストデータを使って予測
y_pred = clf.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

# 分類レポートの表示
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

# 決定木の可視化
plt.figure(figsize=(24, 16))  # 図のサイズを指定
plot_tree(
    clf,  # 学習済みの決定木モデル
    feature_names=iris.feature_names,  # 特徴量の名前
    class_names=iris.target_names,  # クラスの名前
    filled=True,  # ノードを色付け
    rounded=True,  # ノードの角を丸くする
    fontsize=15  # フォントサイズ
)
plt.title("Decision Tree Visualization")  # タイトル
plt.show()

plot_treeメソッドを使用することで、学習済みの決定木モデルをプロットすることが出来る。
なんてこった！

しかも図はかなり良い感じ。

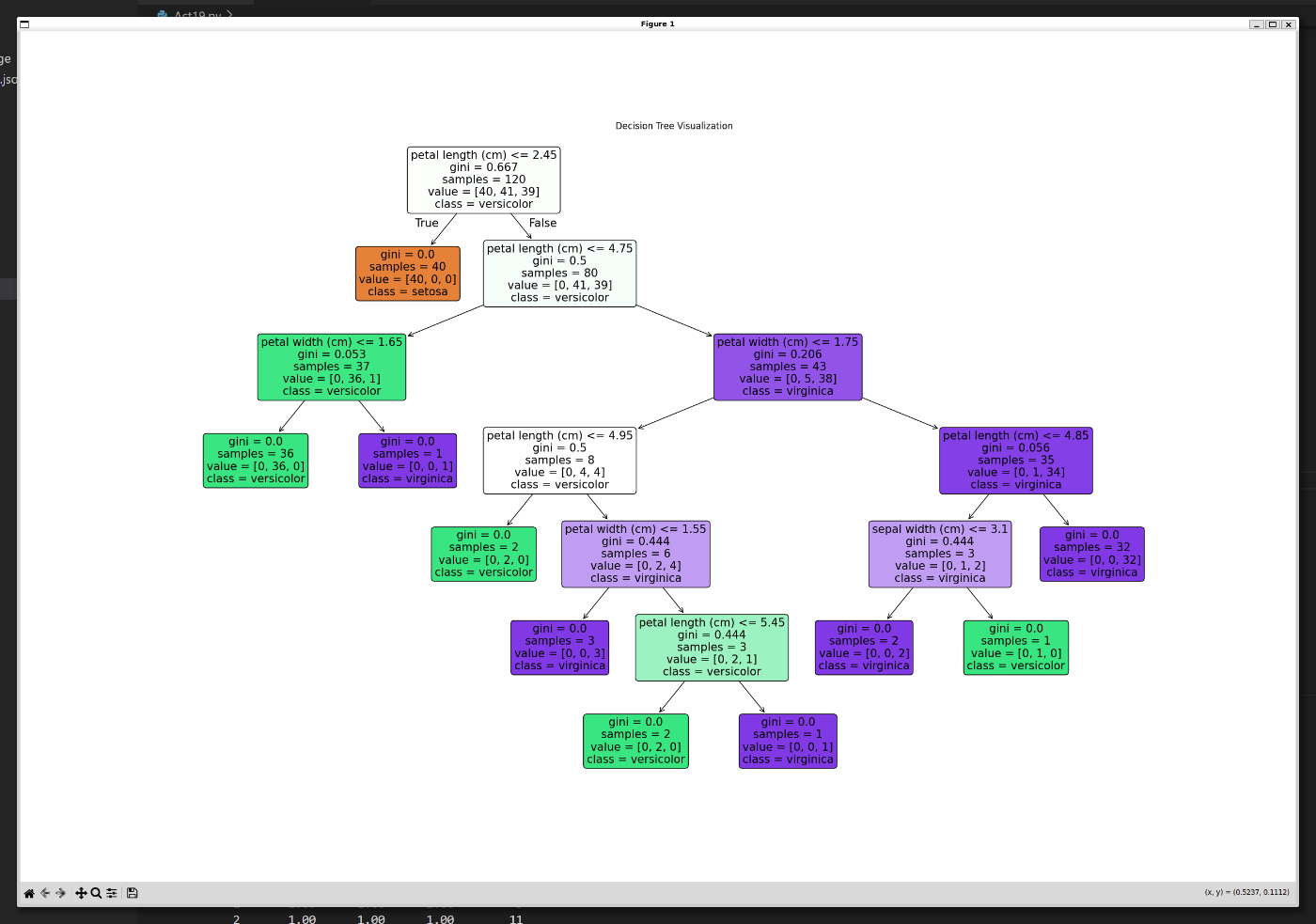
この図の見方について記載しておく。

ルートノード

まずは一番上がルートノードとなる。
ルートノードの内容は以下の通り。

• 条件式: petal length(cm) <= 2.45（花弁の長さが2.45以下かどうか）
• gini: 0.667（ジニ不純度）
• sample: 120（データ数（ルートノードでは全データ））
• value: [40, 41, 39]（各クラスに属するデータ数）
• class: versicolor（そのノードでの最もデータ数の多いクラス）

おっとー、前回学習を回避したジニ不純度がここで出てくるとは…。
エントロピーじゃないんかい！
ジニ不純度については、この記事の補足で解説しているので、わからない人はぜひ読んでほしい。

ちなみに今回のデータは['setosa', 'versicolor', 'virginica']となっている。
これらのデータの特徴量を確認していき、花弁の長さが$2.45$以下の場合はTrue、それ以外はFalseに分類される。

次にルートノードの直下のノードについて。

左側（葉ノード）

• gini: 0（ジニ不純度）
• sample: 40（データ数）
• value: [40, 0, 0]（各クラスに属するデータ数）
• class: setosa（そのノードでの最もデータ数の多いクラス）

花弁の長さが$2.45$以下のデータは全てsetosaという結果らしい。
そのため、不純度は0となり、以降の分類は不要なためここが葉ノードとなる。

右側（内部ノード）

• 条件式: petal length(cm) <= 4.75（花弁の長さが4.75以下かどうか）
• gini: 0.5（ジニ不純度）
• sample: 80（データ数）
• value: [0, 41, 39]（各クラスに属するデータ数）
• class: versicolor（そのノードでの最もデータ数の多いクラス）

setosaのデータは全てTrue側に行ったため、右側の内部ノードのデータ数は$80$となる。
この内部ノードに存在するデータは不純度が$0.5$であるため、さらに分類を行う必要がある。

次の条件式は、花弁の長さが4.75以下かどうか。
直下のノードは以下のように分類された。

左側（内部ノード）

• 条件式: petal width(cm) <= 1.65（花弁の幅が1.65以下かどうか）
• gini: 0.053（ジニ不純度）
• sample: 37（データ数）
• value: [0, 36, 1]（各クラスに属するデータ数）
• class: versicolor（そのノードでの最もデータ数の多いクラス）

ほぼ全てversicolorにすることが出来たが、まだ1つだけvirginicaが存在している。
これをさらに分類したいため、花弁の幅でさらに分類を行っている。

右側（内部ノード）

• 条件式: petal width(cm) <= 1.75（花弁の幅が1.75以下かどうか）
• gini: 0.206（ジニ不純度）
• sample: 43（データ数（ルートノードでは全データ））
• value: [0, 5, 38]（各クラスに属するデータ数）
• class: virginica（そのノードでの最もデータ数の多いクラス）

かなりの数がvirginicaとなっている。
ただ、まだ少しversicolorが残っているため、こちらも花弁の幅で分類を行おうとしている。

以降は同じような流れとなるため説明を割愛する。

補足

ジニ不純度について

ジニ不純度は、分類タスクで使用される不純度の指標で、データがどれだけ「混ざっている」かを数値で表す。

値が 0 に近いほどデータが「純粋」（1つのクラスに集中している）で、1 に近いほど「混ざっている」（複数クラスが均等に含まれている）ことを示す。

ちなみにジニ不純度が0のノードは、それ以上の分類が出来ないため葉ノードとなる。

ジニ不純度の数式

ジニ不純度 $G$ は以下の式で計算される。

$$G = 1 - \sum_{i=1}^K p_i^2$$

• $K$: クラスの総数（例：Irisデータセットでは3クラス）。
• $p_i$: クラス $i$ のデータポイントの割合（確率）。
  • $p_i = \frac{\text{クラス } i \text{ のサンプル数}}{\text{全サンプル数}}$

例で理解する

例 1: 完全に純粋なノード（1つのクラスだけの場合）

ノードに含まれるデータがすべて同じクラス（例：クラス0）ならば

• $p_0 = 1$, $p_1 = 0$, $p_2 = 0$ （クラス0の割合が100%）。

• ジニ不純度

  $$G = 1 - (1^2 + 0^2 + 0^2) = 0$$

このノードは完全に純粋といえる。
エントロピーより簡単すぎるだろ…！

例 2: 均等に混ざったノード（3クラスが同じ割合の場合）

ノードに含まれるデータが3クラス（クラス0, クラス1, クラス2）で均等に分布している場合

• $p_0 = \frac{1}{3}$, $p_1 = \frac{1}{3}$, $p_2 = \frac{1}{3}$。

• ジニ不純度

  $$G = 1 - \left(\left(\frac{1}{3}\right)^2 + \left(\frac{1}{3}\right)^2 + \left(\frac{1}{3}\right)^2\right) = 1 - \left(\frac{1}{9} + \frac{1}{9} + \frac{1}{9}\right) = 1 - \frac{3}{9} = 0.67$$

このノードはかなり混ざっていると言える。

例 3: 一部だけ混ざったノード（2クラスが不均等に分布している場合）

ノードに含まれるデータがクラス0: 80%、クラス1: 20%、クラス2: 0%の場合

• $p_0 = 0.8$, $p_1 = 0.2$, $p_2 = 0$。

• ジニ不純度

  $$G = 1 - \left(0.8^2 + 0.2^2 + 0^2\right) = 1 - (0.64 + 0.04 + 0) = 1 - 0.68 = 0.32$$

このノードはある程度の純度を持っていると言える。

ジニ不純度と決定木

• 分割の評価:
  決定木では、ジニ不純度を使ってノードの「分割の質」を評価する。
  分割後にジニ不純度が低くなるほど、データがクラスごとに純粋に分かれていることを意味する。

• ノード分割のアルゴリズム:
  決定木は、ジニ不純度の減少量（= ジニゲイン）を最大化するように特徴量と分割点を選択する。

なぜジニ不純度を使うのか？

• 計算が簡単（サンプルの割合の2乗を計算するだけ）。
• ノードの純度を直感的に理解しやすい。
• エントロピー（別の不純度指標）に比べて高速に計算できるため、大規模なデータセットに向いている。

さいごに

今まで学習してきた回帰分析も面白かったが、このように図として確認することが出来ると更に面白い。
決定木いいね！

次回はランダムフォレストについて学習する。
「決定木のアンサンブル学習」というものらしいので、きっと決定木同様に楽しいだろう。

ではまた