まえがき
ほぼほぼこちらの論文の抜粋にすぎません。特に断りがない場合、画像はこの論文からの引用です。
定義
ピクセル座標を{\bf u}、3次元点を{\bf x}、3次元点を投影可能な画像領域を\Theta、投影結果が\Thetaに収まるような3次元点全体を\Omegaで表し、それぞれ以下の関係にある。
{\bf u} = [u, v]^T \in \Theta \subset R^2
{\bf x} = [x, y, z]^T \in \Omega \subset R^3
カメラ座標系は、x, y軸が画像座標系のu, v軸に一致しz軸がカメラの光軸に一致するようにとる。
カメラ内部パラメータのベクトルを{\bf i}で表し、カメラによる3次元点の画像面への投影(射影)を\pi : \Omega \to \Theta、逆投影\pi^{-1} : \Theta \to \mathbb{S}^2で表す。
ピンホールカメラモデル
基本形の基本形。魚眼だけでなく通常のレンズのカメラでも利用されている。
内部パラメータは{\bf i} = [f_x, f_y, C_x, C_y]、それぞれx,y軸における焦点距離値および光学中心座標の4パラメータ。
投影\piは次のようになる
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
f_x \frac{x}{z} \\
f_y \frac{y}{z}
\end{array} \right] + \left[ \begin{array}{rrr}
Cx \\
Cy
\end{array} \right]
同次座標系(射影空間)で表すと
\left[ \begin{array}{rrr}
u \\
v \\
w
\end{array} \right] = \left[ \begin{array}{rrr}
f_x & 0 & C_x \\
0 & f_y & C_y \\
0 & 0 & 1
\end{array} \right] \left[ \begin{array}{rrr}
x \\
y \\
z
\end{array} \right]
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
\frac{u}{w} \\
\frac{v}{w}
\end{array} \right]
投影は\Omega = \{ {\bf x} \in \mathbb{R}^3 | z > 0 \}の領域(つまりカメラの前面)で定義され、視野角は180度未満となる。しかし実際には、歪を考慮した場合でも120度を超える視野範囲で最適な性能を発揮しない。
逆投影\pi^{-1}は次のようになる
\pi^{-1}({\bf u, i}) = \frac{1}{\sqrt{m_x^2 + m_y^2 + 1}} \left[\begin{array}{c}
m_x \\
m_y \\
1
\end{array} \right]
m_x = \frac{u - C_x}{f_x}
m_y = \frac{v - C_y}{f_y}
逆投影は\Theta = \mathbb{R}^2(つまり画像平面の全域)で定義される。
Unified Camera Model (UCM)
これはCatadioptric Camera(反射望遠レンズを搭載したカメラ)を表現するために考案されたモデル。魚眼カメラをCentral Catadioptric Camera(カメラの前面に双曲面ミラーを置いたカメラ)と見做す事で魚眼レンズにも適用可能だが完全には適合しないため、追加の歪みモデルと共に使用される。
Central Catadioptric Cameraのイメージ図(H. Ukida, N. Yamato. Omni-directional 3D Measurement by Hyperbolic Mirror Cameras and Pattern Projection. 2008 IEEE Instrumentation and Measurement Technology Conferenceより引用)
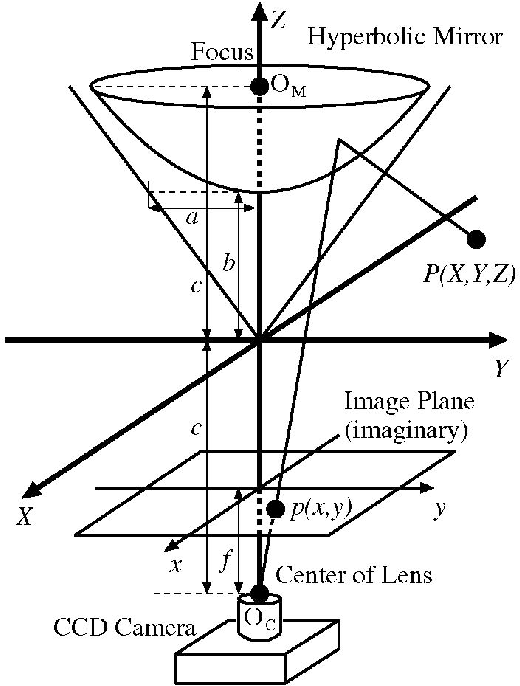
内部パラメータは{\bf i} = [\gamma_x, \gamma_y, C_x, C_y, \xi]の5パラメータ。このモデルでは、3次元点はまず単位球面に投影されてから、ピンホールカメラによって画像面に投影される。\xiは単位球面中心からピンホールカメラ中心までの距離。
UCMによる投影は\piは次のようになる
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
\gamma_x \frac{x}{\xi d+z} \\
\gamma_y \frac{y}{\xi d+z}
\end{array} \right] + \left[ \begin{array}{rrr}
Cx \\
Cy
\end{array} \right]
これだと扱いづらいので、新しいパラメータ\alpha \in [0, 1]を導入して次のように書き直せる。
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
f_x \frac{x}{\alpha d+(1-\alpha)z} \\
f_y \frac{y}{\alpha d+(1-\alpha)z}
\end{array} \right] + \left[ \begin{array}{rrr}
Cx \\
Cy
\end{array} \right]
以前のパラメータとの関係は\gamma_x = \frac{f_x}{1 - \alpha}、\gamma_y = \frac{f_y}{1 - \alpha}、\xi = \frac{\alpha}{1 - \alpha}であり(これは近似ではなく等価な書き換え)、内部パラメータは{\bf i} = [f_x, f_y, C_x, C_y, \alpha]の5パラメータとなる。
c = \alpha d+(1-\alpha)として、投影を同次座標系(射影空間)で表すと次のようになる
\left[ \begin{array}{rrr}
u \\
v \\
w
\end{array} \right] = \left[ \begin{array}{ccc}
f_x & 0 & cC_x \\
0 & f_y & cC_y \\
0 & 0 & c
\end{array} \right] \left[ \begin{array}{c}
x \\
y \\
z
\end{array} \right]
\alpha = 0の時、ピンホールカメラモデルとなる。
投影は以下の領域\Omegaで定義される。
\Omega = \left\{ \begin{array}{ll}
\{ {\bf x} \in \mathbb{R}^3 | z > -d\frac{\alpha}{1-\alpha} \} & (\alpha \leq 0.5) \\
\{ {\bf x} \in \mathbb{R}^3 | z > -d\frac{1-\alpha}{\alpha} \} & (\alpha > 0.5)
\end{array} \right.
逆投影\pi^{-1}は次のようになる
\pi^{-1}({\bf u, i}) = \frac{\xi + \sqrt{1+(1-\xi^2)r^2}}{1 + r^2} \left[ \begin{array}{c}
m_x \\
m_y \\
1
\end{array} \right] -
\left[ \begin{array}{c}
0 \\
0 \\
\xi
\end{array} \right]
m_x = \frac{u - C_x}{f_x}(1-\alpha)
m_y = \frac{v - C_y}{f_y}(1-\alpha)
逆投影は以下の領域\Thetaで定義される
\Theta = \left\{ \begin{array}{ll}
\mathbb{R}^2 & (\alpha \leq 0.5) \\
\{ {\bf u} \in \mathbb{R}^2 | r^2 \leq \frac{(1-\alpha)^2}{2\alpha-1} \} & (\alpha > 0.5)
\end{array} \right.
- C. Geyer and K. Daniilidis. A unifying theory for central panoramic systems and practical implications. In D. Vernon, editor, Computer Vision — ECCV 2000, pages 445–461, Berlin, Heidelberg, 2000. Springer Berlin Heidelberg.
- X. Ying and Z. Hu. Can we consider central catadioptric cameras and fisheye cameras within a unified imaging model. In T. Pajdla and J. Matas, editors, Computer Vision - ECCV 2004, pages 442–455, Berlin, Heidelberg, 2004. Springer Berlin Heidelberg.
Enhanced Unified Camera Model (EUCM)
これはUCMを拡張したモデル。内部パラメータは{\bf i} = [f_x, f_y, C_x, C_y, \alpha, \beta]の6パラメータとなる。\alpha \in [0, 1]、\beta > 0。
EUCMはUCMを一般化したもので、3次元点をz軸に対称な楕円体に投影するようにしたもの。\betaは扁平率(率ではないけど・・・)。
UCM(左)とEUCM(右)の模式図。
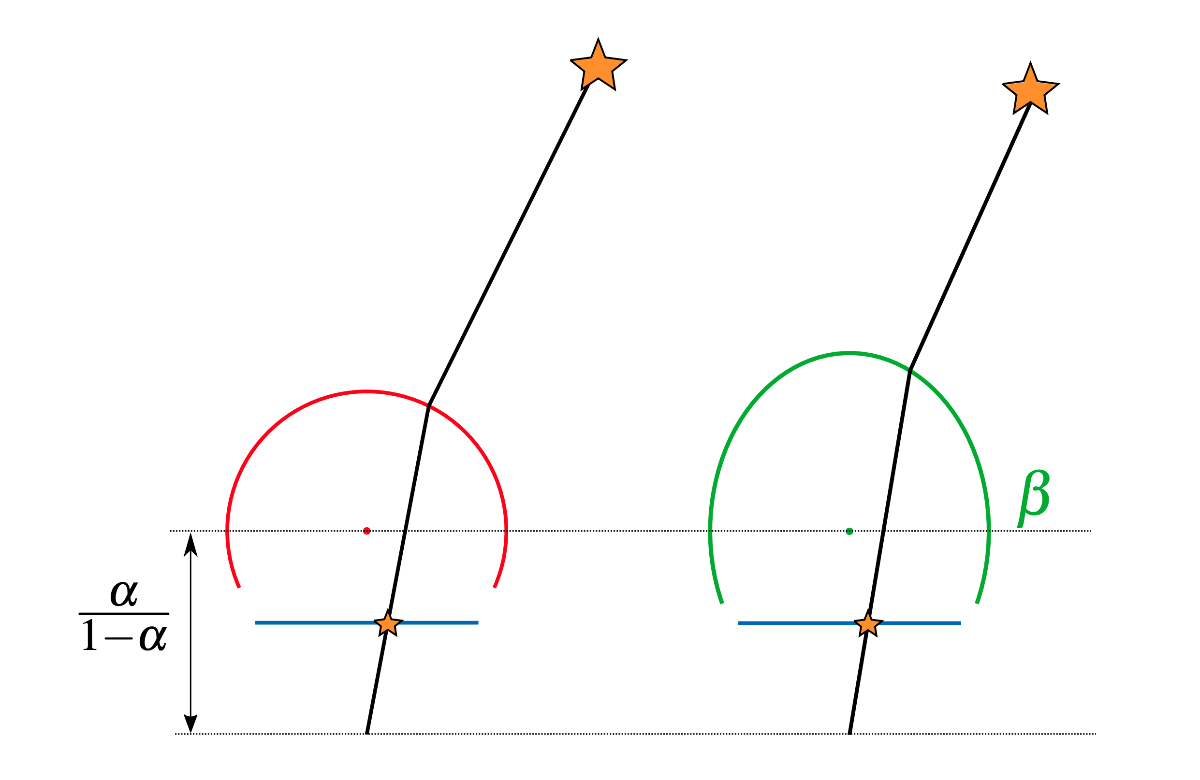
\xi = \frac{\alpha}{1 - \alpha}は、球(楕円)体中心から、ピンホールカメラ中心までのずれ。
EUCMによる投影\piは次のようになる
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
f_x \frac{x}{\alpha d+(1-\alpha)z} \\
f_y \frac{y}{\alpha d+(1-\alpha)z}
\end{array} \right] + \left[ \begin{array}{rrr}
Cx \\
Cy
\end{array} \right]
d = \sqrt{\beta(x^2+y^2)+z^2}
dの定義が異なる以外はUCMとほとんど同じ。同次座標系での表現はこちらのdを用いる以外は全く同じなので省略。また、投影の定義される領域\Omegaもこちらのdを用いる以外は同様。
\beta = 1の時、UCMとなる。
逆投影\pi^{-1}は次のようになる
\pi^{-1}({\bf u, i}) = \frac{1}{\sqrt{m_x^2 + m_y^2 + m_z^2}} \left[ \begin{array}{c}
m_x \\
m_y \\
m_z
\end{array} \right]
m_x = \frac{u - C_x}{f_x}
m_y = \frac{v - C_y}{f_y}
m_z = \frac{1 - \beta\alpha^2 r^2}{\alpha \sqrt{1-(2\alpha-1)\beta r^2}+(1-\alpha)}
EUCMは楕円体に投影しており逆投影のための単位長ベクトルを直接得られないため、正規化によって求める(多分m_zがそれ)。
逆投影は以下の領域\Thetaで定義される
\Theta = \left\{ \begin{array}{ll}
\mathbb{R}^2 & (\alpha \leq 0.5) \\
\{ {\bf u} \in \mathbb{R}^2 | r^2 \leq \frac{1}{\beta(2\alpha-1)} \} & (\alpha > 0.5)
\end{array} \right.
Kannala-Brandt Camera Model (KB)
これは広角レンズと魚眼レンズの両方によく適合するジェネリックなカメラモデル。内部パラメータは{\bf i} = [f_x, f_y, C_x, C_y, k_1, k_2, k_3, k_4]の8パラメータとなるが、k_nの高次のパラメータを落として{\bf i} = [f_x, f_y, C_x, C_y, k_1, k_2]の6パラメータでも利用できる。
このモデルでは、画像面に投影された点と画像中心(光学中心)までの距離が、投影元の3次元点と光軸(カメラ主軸)のなす角度\thetaの多項式d(\theta)に比例することを仮定している。
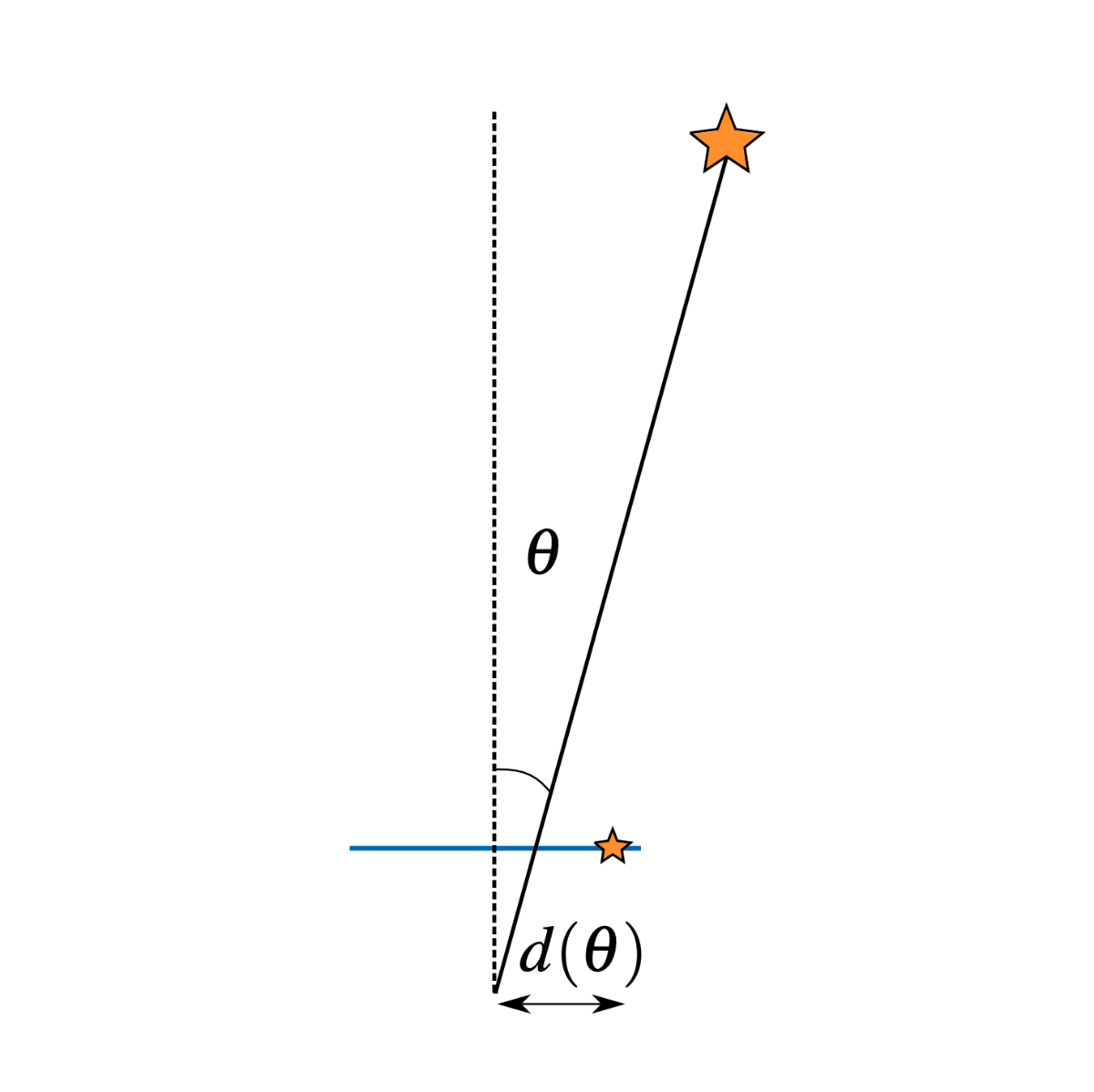
KBによる投影\piは次のようになる
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
f_x d(\theta) \frac{x}{r} \\
f_y d(\theta) \frac{y}{r}
\end{array} \right] + \left[ \begin{array}{rrr}
Cx \\
Cy
\end{array} \right]
d(\theta) = \theta + k_1 \theta^3 + k_2 \theta^5 + k_3 \theta^7 + k_4 \theta^9
投影は\Omega = \mathbb{R}^3 / [0, 0, 0]^Tの領域で定義され、d(\theta)は単調写像であることを仮定する。
パラメータk_nおよびd(\theta)は歪曲収差をモデル化している(図は魚眼カメラモデル (fisheye camera model) - 参考書庫より引用)。
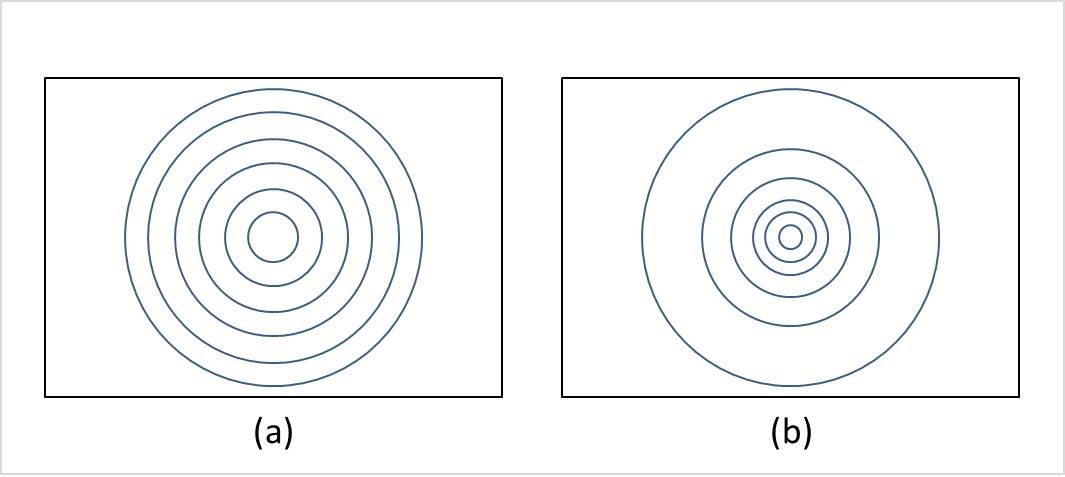
逆投影\pi^{-1}は次のようになる
\pi^{-1}({\bf u, i}) = \left[ \begin{array}{c}
\sin(\theta^*) \frac{m_x}{r_u} \\
\sin(\theta^*) \frac{m_y}{r_u} \\
\cos(\theta^*)
\end{array} \right]
m_x = \frac{u - C_x}{f_x}
m_y = \frac{v - C_y}{f_y}
r_u = \sqrt{m_x^2 + m_y^2}
\theta^*はd(\theta)の逆関数から求める必要がある。d(\theta) = r_uとして、ニュートン法などの反復法によって求めた\thetaを\theta^*とする。
逆投影は\Omega = \mathbb{R}^2で定義される。
KB Modelはピンホールカメラの歪みモデルとしても使用することができる。OpenCVの魚眼レンズのキャリブレーション実装では、KBによってピンホールカメラの歪みとして魚眼レンズをモデル化している。
ただし、歪みモデルとして使用する場合はピンホールカメラとして投影してから歪みを適用するため、z = 0(投影面の半球の地平線の部分)に特異点があり(ピンホールモデルによる投影では、x/z, y/zという計算が入る)、視野角が180度に近い(あるいは180度以上の)魚眼レンズには適さない。OpenCVのcv::fisheye::calibrateは視野角が180度以上と推定されるとassertに引っかかって止まる。
Field-of-View Camera Model (FOV)
内部パラメータは{\bf i} = [f_x, f_y, C_x, C_y, w]の5パラメータ。
このモデルでは、画像面の投影点と画像中心(光学中心)の間の距離が通常、対応する3次元点と光軸(カメラ主軸)のなす角度に比例している事を仮定する。
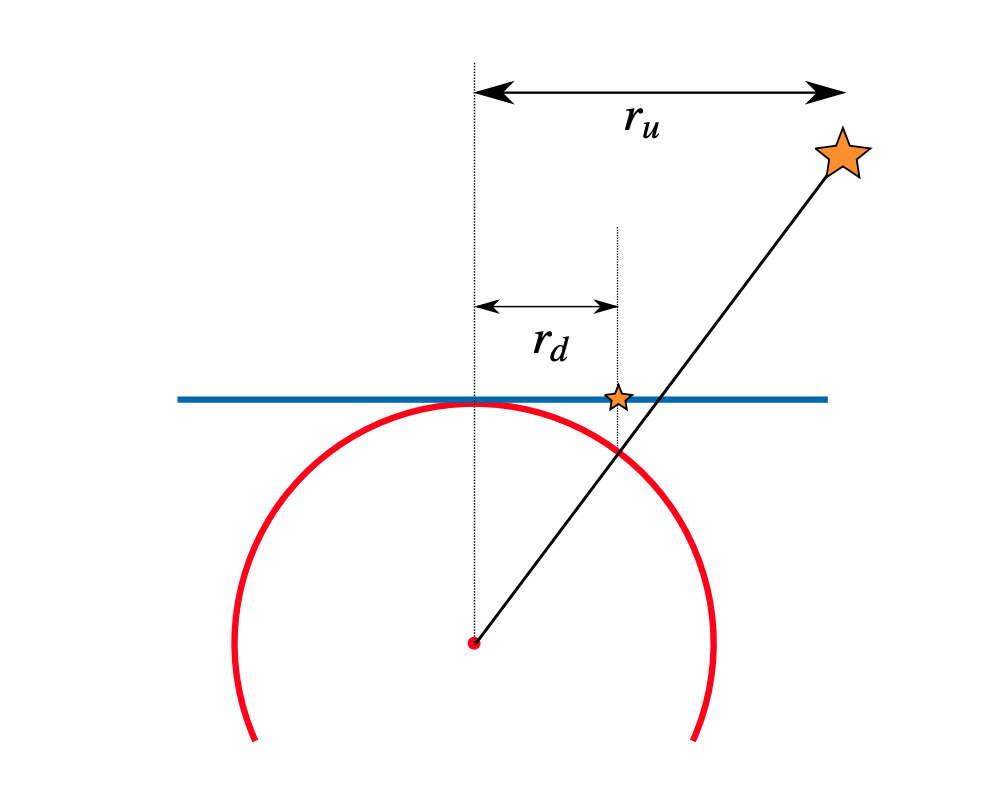
KBによる投影\piは次のようになる
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
f_x r_d \frac{x}{r_u} \\
f_y r_d \frac{y}{r_u}
\end{array} \right] + \left[ \begin{array}{rrr}
Cx \\
Cy
\end{array} \right]
r_d = \frac{atan2(2r_u \tan{\frac{w}{2}}, z)}{w}
投影は\Omega = \mathbb{R}^3 / [0, 0, 0]^Tの領域で定義される
逆投影\pi^{-1}は次のようになる
\pi^{-1}({\bf u, i}) = \left[ \begin{array}{c}
m_x \frac{\sin(r_d w)}{2r_d \tan{\frac{w}{2}}} \\
m_y \frac{\sin(r_d w)}{2r_d \tan{\frac{w}{2}}} \\
\cos(r_d w)
\end{array} \right]
m_x = \frac{u - C_x}{f_x}
m_y = \frac{v - C_y}{f_y}
r_d = \sqrt{m_x^2 + m_y^2}
逆投影は\Omega = \mathbb{R}^2で定義される。
KBモデルと同様に、FOVもピンホールカメラの歪みモデルとして利用できる。
Double Sphere Camera Model (DS)
このモデルは魚眼レンズによく適合し、逆函数が閉形式で記述され、コストの高い三角関数を使用しない。内部パラメータは{\bf i} = [f_x, f_y, C_x, C_y, \xi, \alpha]の6パラメータ。
このモデルでは、3次元点を1つ目の単位球面(緑)に投影した後、中心が\xiだけずれた2つ目の単位球面(赤)に投影し、最後に2つ目の球面の中心から\frac{\alpha}{1-\alpha}だけずれた点をカメラ中心としたピンホールモデルによって画像面に投影される。
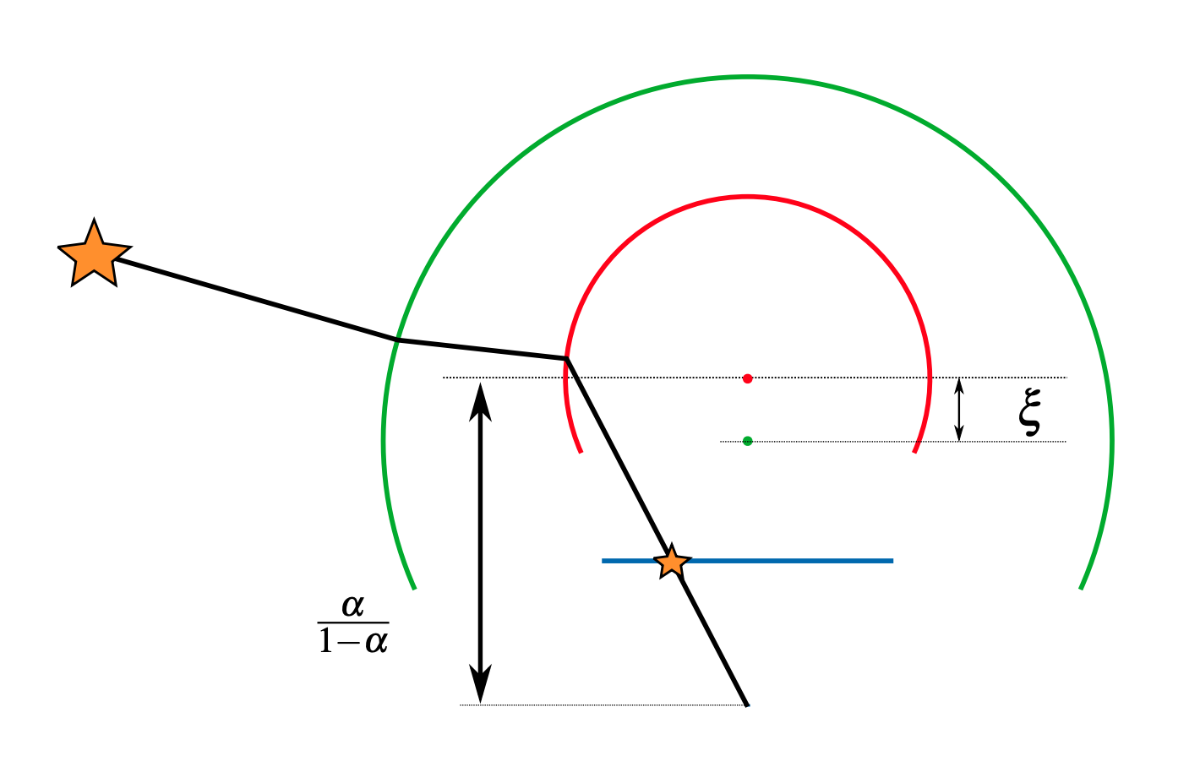
DSによる投影\piは次のようになる
\pi({\bf x, i}) = \left[ \begin{array}{rrr}
f_x \frac{x}{\alpha d_2+(1-\alpha)(\xi d_1+z)} \\
f_y \frac{y}{\alpha d_2+(1-\alpha)(\xi d_1+z)}
\end{array} \right] + \left[ \begin{array}{rrr}
Cx \\
Cy
\end{array} \right]
r_d = \sqrt{x^2+y^2+(\xi d_1+z)^2}
投影は以下の領域\Omegaで定義される。
\Omega = {x \in \mathbb{R}^3 | z > -w_2 d_1}
w_2 = \frac{w_1\xi}{\sqrt{2w_1\xi+\xi^2+1}}
w_1 = \left\{ \begin{array}{ll}
\ \frac{\alpha}{1-\alpha} & (\alpha \leq 0.5) \\
\ \frac{1-\alpha}{\alpha} & (\alpha > 0.5)
\end{array} \right.
逆投影\pi^{-1}は次のようになる
\pi^{-1}({\bf u, i}) = \frac{m_z\xi + \sqrt{m_z^2+(1-\xi^2)r^2}}{m_z^2 + r^2} \left[ \begin{array}{c}
m_x \\
m_y \\
m_z
\end{array} \right] -
\left[ \begin{array}{c}
0 \\
0 \\
\xi
\end{array} \right]
m_x = \frac{u - C_x}{f_x}
m_y = \frac{v - C_y}{f_y}
m_z = \frac{1-\alpha^2 r^2}{\alpha\sqrt{1-(2\alpha-1)r^2}+1-\alpha}
逆投影は以下の領域\Thetaで定義される
\Theta = \left\{ \begin{array}{ll}
\mathbb{R}^2 & (\alpha \leq 0.5) \\
\{ {\bf u} \in \mathbb{R}^2 | r^2 \leq \frac{1}{2\alpha-1} \} & (\alpha > 0.5)
\end{array} \right.
比較?
元の論文に実験結果が記載されている。簡単にまとめると
時間 : EUCM = UCM < DS < KB(6) < KB(8) < FOV
誤差 : KB(8) <= DS <= EUCM <= KB(6) < UCM < FOV
どちらも左にあるほど良い。詳細は元論文参照。
参考文献
関連リンクのメモ
Discussion