【Python】scikit-learnのcalifornia housing datasetを使って回帰分析をしてみる

scikit-learnサイトにはToy dataと言われる様々な公開データがあります。今回はその中の「カリフォルニア住宅価格データセット」を使って単回帰分析や重回帰分析をしてみます。
目次[clickで開く/閉じる]
- データの概要
- データの中身の確認
- 単回帰分析の流れ
- 単回帰分析のソースコード
- 詳細
- 重回帰分析の流れ
- 重回帰分析のソースコード
- 詳細
- まとめ
データの概要
scikit-learnとは、誰もが無料で使えるPythonのオープンソース機械学習ライブラリです。今回はその中でも「california housing dataset」(カリフォルニアの住宅価格データセット)を用いて回帰分析に取り組みます。データセットに含まれる様々な変数から住宅価格を予測することが最終目標です。
では、実際のデータの中身についてみていきましょう。
- データ数:20640
- カラム数:9
| 変数名 | 詳細 |
|---|---|
| Medlnc | 世帯所得の中央値 |
| HouseAge | 住宅の築年数 |
| AveRooms | 住宅の部屋数の平均 |
| AveBedrms | 住宅の寝室数の平均 |
| Poplation | 居住人数の合計 |
| AveOcuup | 世帯人数の平均 |
| Latitude | 各地区における代表地区の緯度 |
| HousePrices | 各地区における代表地区の軽度 |
各データの詳細については以下のscikit-learnのページもご参考ください。
データの中身の確認
まずは必要ライブラリをまとめてインポートしておきましょう。
# 必要ライブラリをインポート
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
インストールしたデータを見てみます。この時についでにデータの大きさやデータの型、欠損値の有無についても確認しておきましょう。今回はきれいなデータですが前処理が必要な場合もありますので...
# データをインポートしてDataFrameの内容とデータ型、欠損の確認をする
from sklearn.datasets import fetch_california_housing
california_housing_data = fetch_california_housing()
# 目的変数
exp_data = pd.DataFrame(california_housing_data.data, columns=california_housing_data.feature_names)
# 説明変数
tar_data = pd.DataFrame(california_housing_data.target, columns=['HousingPrices'])
# データを結合
data = pd.concat([exp_data, tar_data], axis=1)
display(data.head())
print(data.shape) # (20640, 9)
print(data.dtypes) # 全てfloat64
print(data.isnull().sum()) # 全て0
うまくできれば以下のようなデータが出力されるはずです。

では次にデータ同士の相関関係を確認するためにヒートマップを作成してみます。
# ヒートマップを表示
plt.figure(figsize=(12, 9))
sns.heatmap(data.corr(), annot=True, cmap='Blues', fmt='.2f', linewidths=.5)
plt.savefig('california_housing_heatmap.png')
作成したヒートマップがこちらです。

目的変数のHousingPricesに注目してヒートマップを見てみるとMednic, HouseAge, AveRoomsに相関関係があると考えられる。今回の単回帰分析では目的変数をHousingPrices、説明変数をMednicとして進めていくこととします。
単回帰分析の流れ
- データのダウンロード
- データを説明変数と目的変数に分割・外れ値の除去
- 学習
- 予測精度の確認 - 決定係数や回帰直線
- 結果の図示 - 散布図などを使用する
単回帰分析のソースコード
今回は説明変数をMedInc、目的変数をHousingPricesとして進めていきます。以下が単回帰分析のソースコードになります。
exp_var = 'MedInc'
tar_var = 'HousingPrices'
# 散布図を表示
plt.figure(figsize=(12, 9))
plt.scatter(data[exp_var], data[tar_var])
plt.xlabel(exp_var)
plt.ylabel(tar_var)
plt.title('california_housing_scatter')
plt.savefig('california_housing_scatter.png')
data[['MedInc', 'HousingPrices']].describe()
# 外れ値を除去
q_95 = data['MedInc'].quantile(0.95)
print('95%点の分位数', q_95)
# 絞り込む
data = data[data['MedInc'] < q_95]
# 散布図を表示
plt.figure(figsize=(12, 9))
plt.scatter(data[exp_var], data[tar_var])
plt.xlabel(exp_var)
plt.ylabel(tar_var)
plt.title('california_housing_scatter2')
plt.savefig('california_housing_scatter2.png')
plt.show()
# 記述統計量を確認
data[['MedInc', 'HousingPrices']].describe()
# 絞り込む
data = data[data['MedInc'] < q_95]
# 散布図を表示
plt.figure(figsize=(12, 9))
plt.scatter(data[exp_var], data[tar_var])
plt.xlabel(exp_var)
plt.ylabel(tar_var)
plt.savefig('california_housing_scatter2.png')
data[['MedInc', 'HousingPrices']].describe()
# 説明変数と目的変数にデータを分割
X = data[[exp_var]]
print(data.shape)
display(X.head())
y = data[[tar_var]]
print(y.shape)
display(y.head())
# 学習
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
# 精度の確認
print('回帰直線の切片', model.intercept_[0])
print('回帰係数', model.coef_[0][0])
print('決定係数', model.score(X, y))
print('回帰直線', 'y = ', model.coef_[0][0], 'x + ', model.intercept_[0])
# 回帰直線と散布図を表示
plt.figure(figsize=(12, 9))
plt.scatter(X, y)
plt.plot(X, model.predict(X), color='red')
plt.xlabel(exp_var)
plt.ylabel(tar_var)
plt.title('california_housing_regression')
plt.savefig('california_housing_regression.png')
では、ソースコードを分解してみていきましょう。
説明変数と目的変数を指定する
exp_var = 'MedInc' # 説明変数
tar_var = 'HousingPrices' # 目的変数
先ほど全てのデータの中身は確認しましたが、今回使用する2変数のデータの内容を散布図と記述統計量で確認します。
データの内容の確認
# 散布図を表示
plt.figure(figsize=(12, 9))
plt.scatter(data[exp_var], data[tar_var])
plt.xlabel(exp_var)
plt.ylabel(tar_var)
plt.savefig('california_housing_scatter.png')
図示した散布図がこちらです。

# 記述統計量を確認
data[['MedInc', 'HousingPrices']].describe()
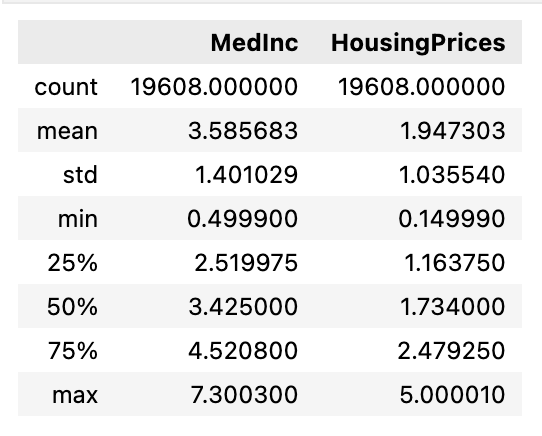
散布図を見るとHousingPrices=5のライン上にデータが集まっていることから外れ値が存在すると考えられます。また記述統計量を見てみるとへHousingPricesの平均値と中央値に大きな差があることから、外れ値が統計をするにあたって大きな影響を与えていることがわかります。以下のコードで外れ値を除去してみます。
# 外れ値を除去
q_95 = data['MedInc'].quantile(0.95)
print('95%点の分位数', q_95)
# 絞り込む
data = data[data['MedInc'] < q_95]
# 散布図を表示
plt.figure(figsize=(12, 9))
plt.scatter(data[exp_var], data[tar_var])
plt.xlabel(exp_var)
plt.ylabel(tar_var)
plt.savefig('california_housing_scatter2.png')
plt.show()
# 記述統計量を確認
data[['MedInc', 'HousingPrices']].describe()
以下に外れ値の影響を小さくして修正したデータに対する散布図と記述統計量を示します。


外れ値の変化は散布図でみるとわかりにくいですが、記述統計量の中央値と平均値の差が修正前よりも小さくなったことがわかると思います。これから修正後のデータを使用して分析を進めていきます。
説明変数と目的変数を設定する
目的変数をexc_var、説明変数をtar_varと表し、列名を指定します。
データフレームを表示する箇所は必要に応じてコメントアウトしてください。
# 説明変数と目的変数にデータを分割
X = data[[exp_var]]
print(data.shape)
display(X.head())
y = data[[tar_var]]
print(y.shape)
display(y.head())
単回帰モデルを学習する
今回のモデルは線形回帰による予測を行うクラスのLinearRegressionとします。LinearRegressionの詳細はこちら。 一番最後の行でデータをモデルに学習させています。
# 学習
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
精度の確認
学習の精度の確認のために回帰直線と決定係数の値を確認します。
# 精度の確認
print('回帰直線の切片', model.intercept_[0])
print('回帰係数', model.coef_[0][0])
print('決定係数', model.score(X, y))
print('回帰直線', 'y = ', model.coef_[0][0], 'x + ', model.intercept_[0])
その結果がこちらになります。

決定係数が約0.197であることから予測精度は悪いことがわかります。やはり1変数だけでは予測が難しそうです。
回帰直線とデータを図示する
学習をもとに得られたデータの図示を行います。回帰直線を赤いラインで示しています。
# 回帰直線と散布図を表示
plt.figure(figsize=(12, 9))
plt.scatter(X, y)
plt.plot(X, model.predict(X), color='red')
plt.xlabel(exp_var)
plt.ylabel(tar_var)
plt.title('california_housing_regression')
plt.savefig('california_housing_regression.png')

では、続いて重回帰分析に取り組んでみましょう。単回帰分析の時と同様にまずは分析の流れについて説明し、その後ソースコードを示してからコードの詳細に触れていきます。今回は目的変数がHousingPrices、説明変数がその他の変数になっています。
重回帰分析の流れ
- 説明変数と目的変数の決定・分割・外れ値の除去
- 説明変数と目的変数それぞれを訓練データとテストデータに分割
- 標準化
- 訓練データの学習
- 学習から得られた予測値・偏回帰係数の確認
- 説明変数と目的変数それぞれでモデルの評価
決定係数や二乗平均誤差(MSE)などを用いる - 正則化の実施 - L1ノルム, L2ノルム
- 精度の比較
今回は通常の正則化しない場合とした場合の精度を比較するために正則化を7.に指定していますが、初めから正則化をする場合は、訓練データの学習のところに追加してください。
重回帰分析のソースコード
# 説明変数
exp_vars = ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
# 目的変数
tar_var = 'HousingPrices'
# 外れ値を除去
for exp_var in exp_vars:
q_95 = data[exp_var].quantile(0.95)
print(exp_var, '95%点の分位数', q_95)
data = data[data[exp_var] < q_95]
# display(data[[exp_var, tar_var]].describe())
# 説明変数と目的変数にデータを分割
X = data[exp_vars]
print(data.shape)
display(X.head())
y = data[[tar_var]]
print(y.shape)
display(y.head())
# 訓練データとテストデータに分割
# 分割のためのモジュールをインポート
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.2, random_state=0)
print('X_train', X_train.shape)
print('y_train', y_train.shape)
print('X_test', len(X_test))
print('y_test', len(y_test))
# X_trainを標準化する
# 標準化ライブラリをインポート
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
print('X_train_scaled', X_train_scaled.shape)
X_train_scaled = pd.DataFrame(X_train_scaled, columns = exp_vars)
display(X_train_scaled.head())
# 学習
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train_scaled, y_train)
# 予測値を計算
y_pred = model.predict(X_train_scaled)
y_pred[:10]
# 偏回帰係数を計算
for xi, wi in zip(exp_vars, model.coef_[0]):
print('{0:7s}: {1:6.3f}'.format(xi, wi))
# 係数を降順に並び替える(係数が大きいと回帰直線に大きな影響を与えていると言える)
import numpy as np
n_list = []
for i in np.argsort(-model.coef_):
n_list = list(i)
for j in n_list:
print('{0:7s}: {1:6.3f}'.format(exp_vars[j], model.coef_[0][j]))
# 精度の確認
# 決定係数
print('決定係数:{:.3f}'.format(model.score(X_train_scaled, y_train)))
from sklearn.metrics import mean_squared_error
# 訓練データに対する Mean Squared Error (MSE)
mse_train = mean_squared_error(y_train, y_pred)
print("訓練データに対するMSE: {:.3f}".format(mse_train))
# テストデータに対する MSE
X_test_scaled = scaler.transform(X_test) # テストデータを訓練データから得られた平均と標準偏差で標準化
y_test_pred = model.predict(X_test_scaled) # テストデータに対して予測する
mse_test = mean_squared_error(y_test, y_test_pred)
print("テストデータに対するMSE: {:.3f}".format(mse_test))
# Ridge回帰
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train_scaled, y_train)
ridge_y_pred = ridge.predict(X_train_scaled)
# 偏回帰係数の確認
ridge_w = pd.DataFrame(ridge.coef_.T, index=exp_vars, columns=['Ridge'])
for xi, wi in zip(exp_vars, ridge.coef_[0]):
print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム: {:.3f}'.format(np.linalg.norm(ridge.coef_)))
# 訓練データに対する Mean Squared Error (MSE)
ridge_mse_train = mean_squared_error(y_train, ridge_y_pred)
print("訓練データに対するMSE: {:.3f}".format(ridge_mse_train))
# テストデータに対する MSE
ridge_y_test_pred = ridge.predict(X_test_scaled) # テストデータに対して予測する
ridge_mse_test = mean_squared_error(y_test, ridge_y_test_pred)
print("テストデータに対するMSE: {:.3f}".format(ridge_mse_test))
# 決定係数
print('決定係数:{:.3f}'.format(ridge.score(X_train_scaled, y_train)))
# Lasso回帰
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0)
lasso.fit(X_train_scaled, y_train)
lasso_y_pred = lasso.predict(X_train_scaled)
# 偏回帰係数の確認
lasso_w = pd.Series(index=exp_vars, data=lasso.coef_)
for xi, wi in zip(exp_vars, lasso.coef_): # coef_は回帰直線の傾き
# print(f'{xi, wi}')
print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム', np.linalg.norm(lasso_w))
lasso_mse_train = mean_squared_error(y_train, lasso_y_pred)
print("訓練データに対するMSE: {:.3f}".format(lasso_mse_train))
lasso_X_test_scaled = scaler.transform(X_test)
lasso_y_pred_test = lasso.predict(lasso_X_test_scaled)
lasso_mse_test = mean_squared_error(y_test, lasso_y_pred_test)
print("テストデータに対するMSE: {:.3f}".format(lasso_mse_test))
# 決定係数
print("決定係数: {:.3f}".format(lasso.score(lasso_X_test_scaled, y_test)))
data = {'訓練データMSE':[mse_train, ridge_mse_train, lasso_mse_train],
'テストデータMSE':[mse_test, ridge_mse_test, lasso_mse_test],
'決定係数':[model.score(X_test_scaled, y_test), ridge.score(X_test_scaled, y_test), lasso.score(X_test_scaled, y_test)]}
df_mse = pd.DataFrame(data=data, index=['重回帰', 'Ridge回帰', 'Lasso回帰'])
df_mse
では、ソースコードを分解してみていきましょう。流れは単回帰の時とほとんど同じです。
説明変数と目的変数を指定する
目的変数をexc_var、説明変数をtar_varとし、データを分割します。
display分やprint文は必要に応じてコメントアウトしてください。
# 説明変数
exp_vars = ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
# 目的変数
tar_var = 'HousingPrices'
データの内容の確認
単回帰分析と同様に外れ値を除去します。
# 外れ値を除去
for exp_var in exp_vars:
q_95 = data[exp_var].quantile(0.95)
print(exp_var, '95%点の分位数', q_95)
data = data[data[exp_var] < q_95]
訓練データとテストデータに分割する
学習用に訓練データとテストデータを8:2に分割します。準備としてデータの標準化を行います。標準化をすることで異なる単位のものを同一尺度で表せるようになります。
# 説明変数と目的変数にデータを分割
X = data[exp_vars]
print(data.shape)
display(X.head())
y = data[[tar_var]]
print(y.shape)
display(y.head())
# X_trainを標準化する
# 標準化ライブラリをインポート
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
print('X_train_scaled', X_train_scaled.shape)
X_train_scaled = pd.DataFrame(X_train_scaled, columns = exp_vars)
display(X_train_scaled.head())
モデルの学習
モデルは単回帰の時と同様にscikit-learnにあるLinearRegressionを使用します。
# 学習
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train_scaled, y_train)
訓練データの予測
訓練データで学習して得られた予測値を表示します。
# 予測値を計算
y_pred = model.predict(X_train_scaled)
y_pred[:10]
# 偏回帰係数を計算
for xi, wi in zip(exp_vars, model.coef_[0]):
print('{0:7s}: {1:6.3f}'.format(xi, wi))
偏回帰係数を見るとMedInc, HouseAge, AveBedrmsがHousingPricesと関係がありそうです。MedInc以外係数がそれほど大きくないので関係があると言い切れないのですが...
予測値が計算できたところで実際のデータと比較してどのくらいの精度で予測ができているのかを確かめます。評価尺度として今回は決定係数と二乗平均誤差を使用します。
モデルの評価
# 決定係数
print('決定係数:{:.3f}'.format(model.score(X_train_scaled, y_train)))
from sklearn.metrics import mean_squared_error
# 訓練データに対する Mean Squared Error (MSE)
mse_train = mean_squared_error(y_train, y_pred)
print("訓練データに対するMSE: {:.3f}".format(mse_train))
# テストデータに対する MSE
X_test_scaled = scaler.transform(X_test) # テストデータを訓練データから得られた平均と標準偏差で標準化
y_test_pred = model.predict(X_test_scaled) # テストデータに対して予測する
mse_test = mean_squared_error(y_test, y_test_pred)
print("テストデータに対するMSE: {:.3f}".format(mse_test))
わたしのマシン上では
- 決定係数:0.564
- 訓練データに対するMSE:0.393
- テストデータに対するMSE:0.372
となりました。
決定係数は1に近いほど精度が高いと言えるので今回のモデルの精度はあまり良くなさそうです。MSEについては訓練データの値とテストデータの値にそれほど差がないので過学習はしていないと考えられます。
では次に正則化を行なった分析もしてみます。
正則化
正則化とは過学習を抑えるための仕組みのひとつで、これを行うことで学習データにモデルが過剰に適合してしまうことで未知のデータに対する予測能力が低下するのを防ぐ役割を持っています。回帰分析における目的は実データに対する予測を行うのであり既知のデータを正確に予測できるだけでは意味がありません。
今回は正則化としてL1ノルムとL2ノルムを用いてLasso回帰とRidge回帰を行います。Ridge回帰はパラメータの値が0となり疎なベクトルになる箇所が多くなるという特徴を持ち、Lasso回帰はパラメータ(今回は偏回帰係数)が小さくなるように学習されるという特徴を持ちます。それでは実際に正則化をやってみます。
# Ridge回帰
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train_scaled, y_train)
ridge_y_pred = ridge.predict(X_train_scaled)
# 偏回帰係数の確認
ridge_w = pd.DataFrame(ridge.coef_.T, index=exp_vars, columns=['Ridge'])
for xi, wi in zip(exp_vars, ridge.coef_[0]):
print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム: {:.3f}'.format(np.linalg.norm(ridge.coef_)))
# 訓練データに対する Mean Squared Error (MSE)
ridge_mse_train = mean_squared_error(y_train, ridge_y_pred)
print("訓練データに対するMSE: {:.3f}".format(ridge_mse_train))
# テストデータに対する MSE
ridge_y_test_pred = ridge.predict(X_test_scaled) # テストデータに対して予測する
ridge_mse_test = mean_squared_error(y_test, ridge_y_test_pred)
print("テストデータに対するMSE: {:.3f}".format(ridge_mse_test))
# 決定係数
print('決定係数:{:.3f}'.format(ridge.score(X_train_scaled, y_train)))
# Lasso回帰
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0)
lasso.fit(X_train_scaled, y_train)
lasso_y_pred = lasso.predict(X_train_scaled)
# 偏回帰係数の確認
lasso_w = pd.Series(index=exp_vars, data=lasso.coef_)
for xi, wi in zip(exp_vars, lasso.coef_): # coef_は回帰直線の傾き
# print(f'{xi, wi}')
print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム', np.linalg.norm(lasso_w))
lasso_mse_train = mean_squared_error(y_train, lasso_y_pred)
print('訓練データに対するMSE', lasso_mse_train)
lasso_X_test_scaled = scaler.transform(X_test)
lasso_y_pred_test = lasso.predict(lasso_X_test_scaled)
lasso_mse_test = mean_squared_error(y_test, lasso_y_pred_test)
print('テストデータに対するMSE', lasso_mse_test)
# 決定係数
print("決定係数: {:.3f}".format(lasso.score(lasso_X_test_scaled, y_test)))

左のデータがRidge回帰で右のデータがLasso回帰です。
Lasso回帰の偏回帰係数が全て0になってしまっているため今回の分析では失敗してしまいました。(🚧現在調整中です🚧)それでは正則化なしの重回帰分析と正則化ありの重回帰分析のどちらの性能が良かったのか精度の比較をしてみます。
data = {'訓練データMSE':[mse_train, ridge_mse_train, lasso_mse_train],
'テストデータMSE':[mse_test, ridge_mse_test, lasso_mse_test],
'決定係数':[model.score(X_test_scaled, y_test), ridge.score(X_test_scaled, y_test), lasso.score(X_test_scaled, y_test)]}
df_mse = pd.DataFrame(data=data, index=['重回帰', 'Ridge回帰', 'Lasso回帰'])
df_mse
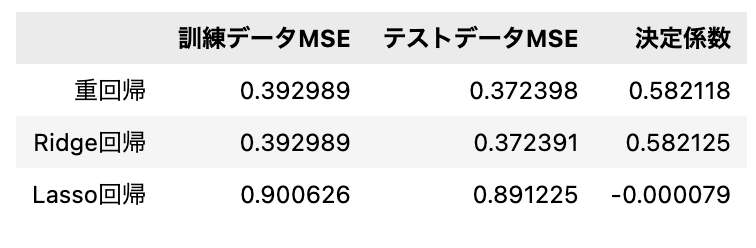
比較すると若干ではありますが、テストデータMSEと決定係数が正則化なしの重回帰分析よりもRidge回帰の方が優れていることがわかります。しかしどのモデルでも決定係数が0.5ほどに留まっていることから精度はよくはありません。より良い精度を出すために単回帰分析で行なった外れ値の除去やハイパーパラメータの設定の変更を行う必要がありそうです。
Discussion