Zenn
🏠

【Python】scikit-learnのboston house prices datasetを使って回帰分析をしてみる

2023/06/16に公開
Python
scikit-learn
データ分析
tech

scikit-learnサイトにはToy dataと言われる様々な公開データがあります。今回はその中の「ボストン住宅価格データセット」を使って単回帰分析や重回帰分析をしてみます。
データはこちらからダウンロードしました。
https://github.com/selva86/datasets/blob/master/BostonHousing.csv

目次[clickで開く/閉じる]
  • データの概要
  • データの中身の確認
  • 単回帰分析の流れ
  • 単回帰分析のソースコード
  • 詳細
  • 重回帰分析の流れ
  • 重回帰分析のソースコード
  • 詳細
  • まとめ

データの概要

scikit-learnとは、誰もが無料で使えるPythonのオープンソース機械学習ライブラリです。今回はその中でも「boston house price dataset」(ボストンの住宅価格データセット)を用いて回帰分析に取り組みます。データセットに含まれる様々な変数から住宅価格を予測することが最終目標です。
　では、実際のデータの中身についてみていきましょう。

  • データ数：506
  • カラム数：14
変数名 詳細
CRIM 人口1人当たりの犯罪発生数
ZN 25000平方フィート以上の居住区間の占める割合
INDUS 小売業以外の商業が占める面積の割合
CHAS チャールズ川によるダミー変数(1:川の周辺,0:それ以外)
NOX NOxの濃度
RM 1940年より前に建てられた物件の割合
DIS 5つのボストン市の雇用施設からの距離
PAD 環状高速道路へのアクセスのしやすさ
TAX ＄10,000ドルあたりの不動産税率の総計
PTRATIO 町毎の児童と教師の比率
B 町毎の黒人（Bk）の比率を次式で表したもの。1000(Bk-0.63)^2
LSTAT 給与の低い職業に従事する人口の割合
MEDV 所有者が占有している家屋の＄1000単位の中央値

参考：https://qiita.com/yut-nagase/items/6c2bc025e7eaa7493f89

データの詳細については以下のscikit-learnのページからもご確認ください。
https://scikit-learn.org/0.19/modules/generated/sklearn.datasets.load_boston.html

※今回の分析では変数Bは除外しています。

データの中身の確認

# データをインポートしてDataFrameの内容とデータ型、欠損の確認をする
import pandas as pd
data = pd.read_csv('boston.csv')
display(data.head())
print(data.shape) # (506, 13)
print(data.dtypes) # 全てfloat64
print(data.isnull().sum()) # 全て0

うまく出力できれば上のようなDataFrameが出てくると思います。この時についでにデータの大きさ、データの型、欠損値の有無についても確認しておきましょう。今回のデータはきれいなデータなので前処理の必要はなさそうです。

#ヒートマップで可視化
import seaborn as sns
import matplotlib.pyplot as plt
heat_map = data.corr(method="pearson")
sns.heatmap(heat_map,center=0,annot=True, cmap="Blues",fmt="1.1f")
plt.savefig('heat_map.png') # 画像の保存

出力したヒートマップがこちらです。

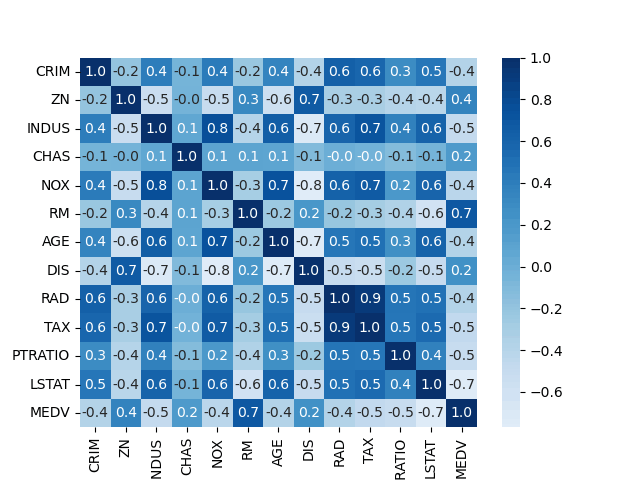
ヒートマップより、今回の目的変数であるMEDVと関係がありそうなのはRMだと仮定できます。部屋数が多いと住宅価格が高くなるのはなんとなくあっていそうに思えます。

では、次から目的変数をMEDV、説明変数をRMとして簡単な単回帰分析をしてみます。
目的変数は予測したい変数で、説明変数は目的変数を予測するのに使う変数を意味しています。

単回帰分析の流れ

  1. データのダウンロード
  2. データを説明変数と目的変数に分ける
  3. 学習
  4. 予測精度の確認 - 決定係数や回帰直線
  5. 結果の図示 - 散布図などを使用する

単回帰分析のソースコード

今回はRMとMEDVについて単回帰分析してみます。以下がソースコードです。

# 説明変数と目的変数を指定する
exp_var = 'RM' # 部屋数(RM)を説明変数
tar_var = 'MEDV' # 住宅価格(MEDV)を説明変数

# 説明変数をDataFrameにする
X = data[[exp_var]]
X.head()

# 目的変数をDataFrameにする
y = data[[tar_var]]
y.head()

# 単回帰モデルを学習する
# 線形回帰による予測を行うクラスLinearRegression()をインストールする
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X, y)
print('回帰直線の切片', lr.intercept_)
print('回帰係数', lr.coef_[0])
print('決定係数', lr.score(X, y))
print('回帰係数', 'y = ', lr.coef_[0], 'x' , '+',  lr.intercept_)

plt.scatter(X, y) # 散布図を描画
plt.plot(X, lr.predict(X), color="r") # 回帰直線を赤い直線で描画
plt.xlabel(f"{exp_var}") 
plt.ylabel(f"{tar_var}")

plt.scatter(X, y) # 散布図を描画
plt.plot(X, lr.predict(X), color="r") # 回帰直線を赤い直線で描画
plt.xlabel(f"{exp_var}") 
plt.ylabel(f"{tar_var}")
plt.show()

import numpy as np
r = np.corrcoef(data['RM'], data['MEDV'])[0][1]
print('相関係数', r)
print('相関係数^2（決定係数の2乗になっていることを確認）', r ** 2)
print('決定係数',lr.score(X, y))

では、ソースコードを分解してみていきましょう。

説明変数と目的変数を指定する

目的変数をexc_var、説明変数をtar_varと表し、列名を指定します。
データフレームを表示する箇所は必要に応じてコメントアウトしてください。

exp_var = 'RM' # 部屋数(RM)を説明変数
tar_var = 'MEDV' # 住宅価格(MEDV)を説明変数

# 説明変数をDataFrameにする
X = data[[exp_var]]
X.head() # 表示
# 目的変数をDataFrameにする
y = data[[tar_var]]
y.head() # 表示

単回帰モデルを学習する

今回のモデルは線形回帰による予測を行うクラスのLinearRegressionとします。LinearRegressionの詳細はこちら。
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
一番最後の行でデータをモデルに学習させています。

# 単回帰モデルを学習する
# 線形回帰による予測を行うクラスLinearRegression()をインストールする
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X, y)

精度の確認

print('回帰直線の切片', lr.intercept_[0])
print('回帰係数', lr.coef_[0][0])
print('決定係数', lr.score(X, y))
print('回帰係数', 'y = ', lr.coef_[0][0], 'x' , '+',  lr.intercept_[0])

回帰直線とデータを図示する

plt.scatter(X, y) # 散布図を描画
plt.plot(X, lr.predict(X), color="r") # 回帰直線を赤い直線で描画
plt.xlabel(f"{exp_var}") 
plt.ylabel(f"{tar_var}")
plt.show()

散布図と回帰直線を図示すると以下のようになります。

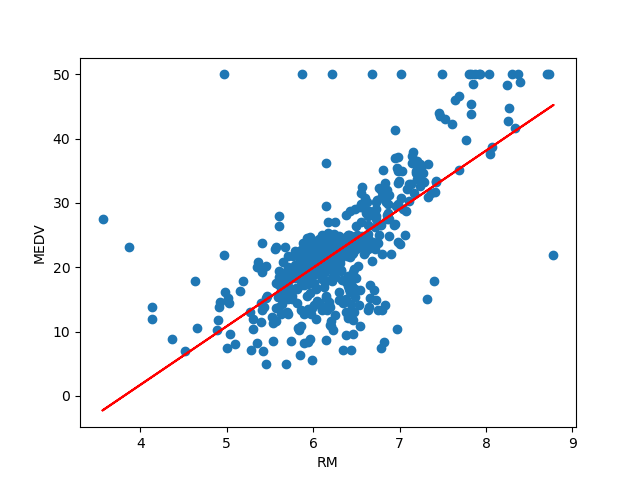
決定係数の値が約0.48となっていることから予測精度はあまり良くないことがわかります。プロットされたデータを見てみるとMEDV=50のラインにデータが集まっており、これらは外れ値である可能性が高いです。より良い精度を求めるのであれば外れ値を除外したデータで分析してみる方がいいかもしれません。

では、続いて重回帰分析に取り組んでみましょう。単回帰分析の時と同様にまずは分析の流れについて説明し、その後ソースコードを示してからコードの詳細に触れていきます。今回は目的変数がMEDV、説明変数がその他の変数になっています。

重回帰分析の流れ

  1. 説明変数と目的変数の決定・分割
  2. 説明変数と目的変数それぞれを訓練データとテストデータに分割
    　　大体、説明変数：目的変数 = 8 : 2とする場合が多いようです。
  3. 標準化
  4. 訓練データの学習
  5. 学習から得られた予測値・偏回帰係数の確認
  6. 説明変数と目的変数それぞれでモデルの評価
    　　決定係数や二乗平均誤差（MSE）などを用いる
  7. 正則化の実施 - L1ノルム, L2ノルム
  8. 精度の比較

今回は通常の正則化しない場合とした場合の精度を比較するために正則化を7.に指定していますが、初めから正則化をする場合は、訓練データの学習のところに追加してください。

重回帰分析のソースコード

# 説明変数
exp_vars = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'LSTAT']
# 目的変数
tar_var = "MEDV"
X = data[exp_vars]
display(X.shape)
X.head()
y = data[tar_var]
display(y.shape)
y.head()
# train_data, test_dataに分割
# train_data : test_data = 8:2

# 訓練データとテストデータに分割するためのモデル
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
print('X_train', X_train.shape)
print('y_train', y_train.shape)
print('X_test', len(X_test))
print('y_test', len(y_test))

# データを標準化するためのモデル
from sklearn.preprocessing import StandardScaler
# X_trainを標準化する
scaler = StandardScaler()
scaler.fit(X_train) 
X_train_scaled = scaler.transform(X_train)
df_scaled = pd.DataFrame(scaler.transform(X_train), columns=X_train.columns)
df_scaled.head(10) # 標準化されたデータの先頭10件 を試しに見てみる

# 学習
# 訓練データからパラメータ（回帰直線の傾き）を学習している
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)

# 予測値の確認
y_pred = lr.predict(X_train_scaled)
y_pred[1:10]

# 偏回帰係数の確認
for xi, wi in zip(exp_vars, lr.coef_): # coef_は回帰直線の傾き
    # print(xi)
    # print(wi)
    # print(f'{xi, wi}')
    print('{0:7s}: {1:6.3f}'.format(xi, wi))

# 係数を降順に並び替える（係数が大きいと回帰直線に大きな影響を与えていると言える）
import numpy as np
for i in np.argsort(-lr.coef_):
    # print(i) # iには値が大きい順にインデックスが打たれている
    print('{0:7s}: {1:6.3f}'.format(exp_vars[i], lr.coef_[i]))
    
# 決定係数
print("決定係数: {:.3f}".format(lr.score(X_test_scaled, y_test)))
w = pd.Series(index=exp_vars, data=lr.coef_)
np.linalg.norm(w, ord=2) # 重みベクトルwの L2ノルム
# np.linalg.norm(w) # 重みベクトルwの L1ノルム

# 訓練データに対するMSE
from sklearn.metrics import mean_squared_error
mse_train = mean_squared_error(y_train, y_pred)
print('訓練データに対するMSE', mse_train)

# テストデータに対するMSE
X_test_scaled = scaler.transform(X_test)
y_pred_test = lr.predict(X_test_scaled)
mse_test = mean_squared_error(y_test, y_pred_test)
print('テストデータに対するMSE', mse_test)

# Ridge回帰
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train_scaled, y_train)
y_pred = ridge.predict(X_train_scaled)
# 偏回帰係数の確認
w_ridge = pd.Series(index=exp_vars, data=ridge.coef_)
for xi, wi in zip(exp_vars, ridge.coef_): # coef_は回帰直線の傾き
    # print(f'{xi, wi}')
    print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム', np.linalg.norm(w_ridge))
# 訓練データに対するMSE
ridge_mse_train = mean_squared_error(y_train, y_pred)
print('訓練データに対するMSE', ridge_mse_train)
# テストデータに対するMSE
X_test_scaled = scaler.transform(X_test)
y_pred_test = ridge.predict(X_test_scaled)
ridge_mse_test = mean_squared_error(y_test, y_pred_test)
print('テストデータに対するMSE', ridge_mse_test)
# 決定係数
print("決定係数: {:.3f}".format(ridge.score(X_test_scaled, y_test)))

# Lasso回帰
from sklearn.linear_model import Ridge
lasso = Lasso(alpha=1.0)
lasso.fit(X_train_scaled, y_train)
y_pred = lasso.predict(X_train_scaled)
# 偏回帰係数の確認
w_lasso = pd.Series(index=exp_vars, data=lasso.coef_)
for xi, wi in zip(exp_vars, lasso.coef_): # coef_は回帰直線の傾き
    # print(f'{xi, wi}')
    print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム', np.linalg.norm(w_ridge))
# 訓練データに対するMSE
lasso_mse_train = mean_squared_error(y_train, y_pred)
print('訓練データに対するMSE', lasso_mse_train)
# テストデータに対するMSE
X_test_scaled = scaler.transform(X_test)
y_pred_test = lasso.predict(X_test_scaled)
lasso_mse_test = mean_squared_error(y_test, y_pred_test)
print('テストデータに対するMSE', lasso_mse_test)
# 決定係数
print("決定係数: {:.3f}".format(lasso.score(X_test_scaled, y_test)))

# 精度の比較
data = {'訓練データMSE':[mse_train, ridge_mse_train, lasso_mse_train], 
        'テストデータMSE':[mse_test, ridge_mse_test, lasso_mse_test], 
        '決定係数':[lr.score(X_test_scaled, y_test), ridge.score(X_test_scaled, y_test), lasso.score(X_test_scaled, y_test)]}
df_mse = pd.DataFrame(data=data, index=['重回帰', 'Ridge', 'Lasso'])
df_mse

では、ソースコードを分解してみていきましょう。流れは単回帰の時とほとんど同じです。

説明変数と目的変数を指定する

目的変数をexc_var、説明変数をtar_varと表し、列名を指定します。
データフレームを表示する箇所は必要に応じてコメントアウトしてください。

# 説明変数を12個用意
exp_vars = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'LSTAT'] 
#目的変数
tar_var = "MEDV" 

# 説明変数をDataFrameにする
X = data[exp_vars]
display(X.shape)
X.head() # 表示
# 目的変数をDataFrameにする
y = data[tar_var]
display(y.shape)
y.head() # 表示

訓練データとテストデータに分割する

学習用に訓練データとテストデータを8:2に分割します。準備としてデータの標準化を行います。標準化をすることで異なる単位のものを同一尺度で表せるようになります。

# データを標準化するためのモデル
from sklearn.model_selection import train_test_split
# 訓練データとテストデータに分割するためのモデル
from sklearn.preprocessing import StandardScaler

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
print('X_train', X_train.shape) # 確認
print('y_train', y_train.shape) # 確認
print('X_test', len(X_test)) # 確認
print('y_test', len(y_test)) # 確認

# X_trainを標準化する
scaler = StandardScaler()
scaler.fit(X_train) 
X_train_scaled = scaler.transform(X_train)
df_scaled = pd.DataFrame(scaler.transform(X_train), columns=X_train.columns)
df_scaled.head(10) # 標準化されたデータの先頭10件 を試しに見てみる

モデルの学習

モデルは単回帰の時と同様にscikit-learnにあるLinearRegressionを使用します。

# 学習
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)

訓練データの予測

訓練データで学習して得られた予測値を表示します。

# 予測値の表示
y_pred = lr.predict(X_train_scaled)
y_pred[1:10] # 予測値の上位10件を表示

# 偏回帰係数の確認
for xi, wi in zip(exp_vars, lr.coef_): # coef_は回帰直線の傾き
    # print(xi)
    # print(wi)
    # print(f'{xi, wi}')
    print('{0:7s}: {1:6.3f}'.format(xi, wi))
    
# 係数を降順に並び替える（係数が大きいと回帰直線に大きな影響を与えていると言える）
import numpy as np
for i in np.argsort(-lr.coef_):
    print('{0:7s}: {1:6.3f}'.format(exp_vars[i], lr.coef_[i]))

偏回帰係数を降順にした結果がこちらです。

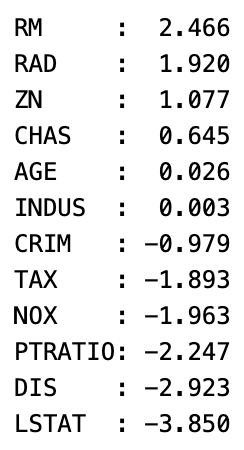
モデルの評価

まずは訓練データとテストデータに対する二乗平均誤差（Mean Squared Error : MSE）をそれぞれ求めます。

# 訓練データに対するMSE
from sklearn.metrics import mean_squared_error
mse_train = mean_squared_error(y_train, y_pred)
print('訓練データに対するMSE', mse_train)

# テストデータに対するMSE
X_test_scaled = scaler.transform(X_test)
y_pred_test = lr.predict(X_test_scaled)
mse_test = mean_squared_error(y_test, y_pred_test)
print('テストデータに対するMSE', mse_test)

# 決定係数
print("決定係数: {:.3f}".format(lr.score(X_test_scaled, y_test)))

正則化

正則化とは過学習するのを抑える仕組みで、学習するときにパラメータ（学習により決められる変数のこと）が大きくなるごとにペナルティを与えることとしています。パラメータが訓練データに過学習してしまうと繁華能力がなくなりテストデータの予測制度が落ちてしまう可能性があります。今回はL1ノルムとL2ノルムを用います。

# Ridge回帰
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train_scaled, y_train)
y_pred = ridge.predict(X_train_scaled)

# 偏回帰係数の確認
w_ridge = pd.Series(index=exp_vars, data=ridge.coef_)
for xi, wi in zip(exp_vars, ridge.coef_): # coef_は回帰直線の傾き
    # print(f'{xi, wi}')
    print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム', np.linalg.norm(w_ridge))

# 訓練データに対するMSE
ridge_mse_train = mean_squared_error(y_train, y_pred)
print('訓練データに対するMSE', ridge_mse_train)

# テストデータに対するMSE
X_test_scaled = scaler.transform(X_test)
y_pred_test = ridge.predict(X_test_scaled)
ridge_mse_test = mean_squared_error(y_test, y_pred_test)
print('テストデータに対するMSE', ridge_mse_test)

# 決定係数
print("決定係数: {:.3f}".format(ridge.score(X_test_scaled, y_test)))

# Lasso回帰
from sklearn.linear_model import Ridge
lasso = Lasso(alpha=1.0)
lasso.fit(X_train_scaled, y_train)
y_pred = lasso.predict(X_train_scaled)

# 偏回帰係数の確認
w_lasso = pd.Series(index=exp_vars, data=lasso.coef_)
for xi, wi in zip(exp_vars, lasso.coef_): # coef_は回帰直線の傾き
    # print(f'{xi, wi}')
    print('{0:7s}: {1:6.3f}'.format(xi, wi))
print('L2ノルム', np.linalg.norm(w_ridge))

# 訓練データに対するMSE
lasso_mse_train = mean_squared_error(y_train, y_pred)
print('訓練データに対するMSE', lasso_mse_train)

# テストデータに対するMSE
X_test_scaled = scaler.transform(X_test)
y_pred_test = lasso.predict(X_test_scaled)
lasso_mse_test = mean_squared_error(y_test, y_pred_test)
print('テストデータに対するMSE', lasso_mse_test)

# 決定係数
print("決定係数: {:.3f}".format(lasso.score(X_test_scaled, y_test)))

それぞれの回帰分析の評価としてMSEと決定係数の値を重回帰、Ridge回帰、Lasso回帰で比較してみます。

data = {'訓練データMSE':[mse_train, ridge_mse_train, lasso_mse_train], 
        'テストデータMSE':[mse_test, ridge_mse_test, lasso_mse_test], 
        '決定係数':[lr.score(X_test_scaled, y_test), ridge.score(X_test_scaled, y_test), lasso.score(X_test_scaled, y_test)]}
df_mse = pd.DataFrame(data=data, index=['重回帰', 'Ridge', 'Lasso'])

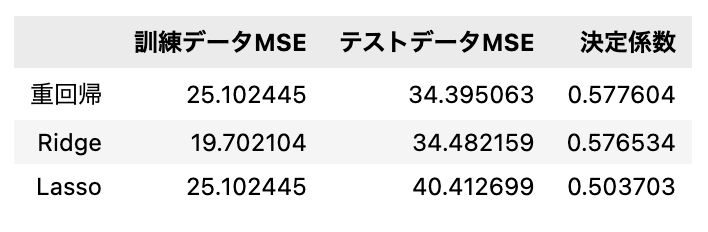
比較によりテストデータにおけるRidge回帰のMSEが一番小さく決定係数も約0.576となっているため今回のモデルの中ではRidge回帰が正解に近い予測ができたと考えられます。しかし、あまり精度は良くないですね...

まとめ

以上がboston house prices datasetを使用した回帰分析になります。学習のモデルやパラメータを変えることでより精度の高い予測ができますので試してみてください。

これからもscikit-learn公開データを使用してデータ分析を行なっていきますので皆さんも一緒に挑戦してみましょう。

参考にさせていただいたサイト

Discussion