Zenn
Open29

Python3エンジニア認定データ分析試験勉強メモ

機械学習
pandas
データ分析
Python 3
#
資格
おみずのみ太郎おみずのみ太郎

2023年8月ごろ、この試験受験しました。
私の勉強方法はチートシートを手書きでメモって丸暗記するスタイルです。
せっかくまとめたし、どんどん勉強した内容を忘却していくので
チートシートを記録に残しておこうと思います。

このチートシートは試験受験前に問題集や参考書をもとに作成したものです。
当該内容が試験に出題されることを保証するものではありません。
また個人の勉強のためにメモした内容ですので内容に誤りがある可能性がありますのでご注意ください。

おみずのみ太郎おみずのみ太郎

DBSCANクラスタリング

  • 密度準拠クラスタリングアルゴリズム。
  • 半径以内に点がいくつあるかでクラス分けする。
  • 長所
    • クラスタ数を決める必要がない。
    • とがったクラスタでも分類できる。
  • 短所
    • 計算コストが高い。
    • データが密集している場合に不向き。
おみずのみ太郎おみずのみ太郎

Flake8, PycodeStyle

  • PycodeStyle
    • PEP8に違反していないかチェックをする。
  • Flake 8
    • プログラムの論理的なチェックをする。
おみずのみ太郎おみずのみ太郎

loggingのログレベル

重要度は低い→高い順に

  • Debug
  • Info
  • Warnning
  • Error
  • Critical

デフォルトはWarnning, Error, Critival

おみずのみ太郎おみずのみ太郎

Jupyter Note マジックコマンド

%または%%

  • 実行時間を計算
    !または!!
  • シェル実行

%timeit

  • セル内の一行のプログラムの実行時間を計測する。
    %timeit
  • セル全体のプログラム実行時間を計測する。
    %lsmagic
  • マジックコマンドの一覧表示
おみずのみ太郎おみずのみ太郎

ベクトルの足し算

x + y = \left( \begin{matrix} x_1 + y_1 \\ x_2 + y_2 \\ ・\\ ・\\ ・\\ x_n + y_n \end{matrix} \right)

ベクトルの引き算

x - y = \left( \begin{matrix} x_1 - y_1 \\ x_2 - y_2 \\ ・\\ ・\\ ・\\ x_n - y_n \end{matrix} \right)

ベクトルのかけ算

ax = \left( \begin{matrix} ax_1\\ ax_2\\ ・\\ ・\\ ・\\ ax_n \end{matrix} \right)
おみずのみ太郎おみずのみ太郎

行列の列数とベクトルのサイズが同じ場合
かけ算の結果は元の行列の行数と同じサイズのベクトルになる。

\left( \begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix} \right) \left( \begin{matrix} 1 & 2 \\ \end{matrix} \right) = (1×1 + 2×2, 1×3 + 4×2, 5×1 + 6×2)\\ =(5, 11, 17)
おみずのみ太郎おみずのみ太郎

行列のたし算、引き算

A±B = \left( \begin{matrix} a_{11} ± b_{11} & a_{12} ± b_{12} ・・・ a_{1n} ± b_{1n} \\ a_{11} ± b_{11} & a_{12} ± b_{12} ・・・ a_{1n} ± b_{1n} \\ ・\\ ・\\ ・\\ a_{m1} ± b_{m1} & a_{m2} ± b_{m2} ・・・ a_{mn} ± b_{mn} \\ \end{matrix} \right)
おみずのみ太郎おみずのみ太郎

行列のかけ算

  • 行列のかけ算の順番を入れ替えると結果が同じになるとは限らない。
  • 単位行列の場合は同じになる。
  • m × n の行列に s × nの行列をかけると m × n の行列になる。
\left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right) \left( \begin{matrix} 5 & 7 \\ 6 & 8 \end{matrix} \right) = \left( \begin{matrix} 1 × 5 + 2 × 6 & 1 × 7 + 2 × 8 \\ 3 ×5 + 4 × 6 & 3 × 7 + 4 × 8 \end{matrix} \right) = \left( \begin{matrix} 17 & 23 \\ 39 & 53 \end{matrix} \right)
おみずのみ太郎おみずのみ太郎

対数の性質

・log_{A}A^m = m
・log_{A}A = 1
・log_{A}1 = 0
・log_{A}\frac{1}{A} = -1
・log_{A}\frac{1}{N} = - log_{A}N

おみずのみ太郎おみずのみ太郎

Shapeの動作

  • ndarrayのshapeは各次元ごとの要素数が出力される。

    a = np.array([5, 3, 8, 9])
a.shape

  • 結果

    (4,)

  • 2次元配列の場合は以下のように出力される。

    a = np.array([[5, 3, 8, 9]])
a.shape

  • 結果

    (1,4)
おみずのみ太郎おみずのみ太郎

arangeの動作

  • 出力結果の初要素は引数で指定した値になる。
  • 最終要素は引数に指定した値になるとはかぎらない。
np.arange(1, 10, 2)

結果

array([1, 3, 5, 7, 9])
おみずのみ太郎おみずのみ太郎

linspaceの動作

初要素と最終要素は引数で指定した値になる。

np.linespace(0, 1, 5)

結果

array([0, 0.25, 0.5, 0.75, 1])
おみずのみ太郎おみずのみ太郎

■pd.grouper
時系列データを日時・週次・月次でそれぞれ集計する。

df.groupby(pd.Grouper(freq='M')).mean()
freq 集計内容
W 週次集計
M 月次集計
W-SUN 日曜を軸に集計(Wと同じ)
W-MON 月曜を軸に集計(W-MONと同じ)
W-TUE 火曜を軸に集計(W-TUEと同じ)
おみずのみ太郎おみずのみ太郎

■Matplotlib
pyplotインターフェース

  • MATLABと似た形でグラフを描画する。
  • グラフを描画するため各種関数を実行する。
  • 冗長なスクリプトになる。

オブジェクト指向インターフェース

  • 描画オブジェクトにサブプロットを追加する。
  • figureオブジェクトに複数サブプロットを指定できる。
おみずのみ太郎おみずのみ太郎

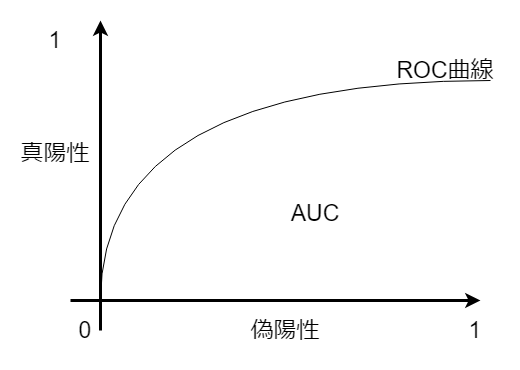
■AUC

  • ROC曲線の下の面積を表す指標
  • 2値分類モデルの性能評価に使用する
  • 0 <= AUC <=1となる。
  • 横軸に偽陽性率
  • 縦軸に真陽性率
おみずのみ太郎おみずのみ太郎

■Matplotlib legend loc引数候補
‘best’
‘upper right’
‘upper left’
‘lower left’
‘lower right’
‘right’
‘center left’
‘center right’
‘lower center’
‘upper center’
‘center’

おみずのみ太郎おみずのみ太郎

■random一覧

  • rand.random()
    0.0以上1.0未満の浮動小数点数。引数にタプルをとる
  • rand.uniform()
    任意の範囲の浮動小数点数
  • np.random.randint()
    ランダムな整数を返す
  • np.random.normal()
    正規分布の乱数を返す
  • randint(最小値, 最大値, 配列形状)
  • normal(平均,標準偏差,サイズ)
  • np.random.randn(平均0, 分散1)
    正規分布の乱数を生成する
おみずのみ太郎おみずのみ太郎

■特徴量の正規化

  • 特徴量の大きさを揃える処理
  • ある特徴量の値が2桁で数十のオーダーの場合と4桁で数千のオーダーの場合
    　4桁数千が大きな影響を受ける。
  • そのため尺度を揃える

分散正規化
特徴量の平均が0,標準偏差が1となるよう変換する処理
最大最小正規化
最大が1,最小が0となるよう正規化する処理

おみずのみ太郎おみずのみ太郎

■決定木
情報利得=親ノードの不純度-子ノードの不純度

不純度指標には、ジニ不純度、エントロピー、分類誤差がある

おみずのみ太郎おみずのみ太郎

■サポートベクタマシン

  • 分類、回帰、外れ値検出に使用できる
  • データを高次元の空間に写して線形分離することにより分類を行う。
おみずのみ太郎おみずのみ太郎

■サポートベクタマシンの決定境界とマージン

  • データ間の距離が最大になる直線を決定境界という
  • 各クラスのデータをサポートベクタという
  • サポートベクタの距離をマージンと呼ぶ
  • マージンを最大にすることにより決定境界を求める
おみずのみ太郎おみずのみ太郎

■カテゴリ分類精度

  • 適合率＝tp/(tp+fp)
    →正例と予測して実際に正例であった割合

  • 再現率=tp/(tp+fn)
    →実際に正例のうち、正例と予測したものの割合

  • 適合率と再現率はトレードオフ

  • F値=2(1/適合率 + 1/再現率)
    = 2 ×適合率×再現率/(適合率 + 再現率)

  • F値は適合率と再現率の調和平均

  • 正解率=(tp+tn)/(tp+fp+fn+tn)

  • 正例、不例問わず、予測と実績が一致したデータの割合を表す

おみずのみ太郎おみずのみ太郎

■クラスタリング
・Kmeans
・階層的クラスタリング

  • ぎ集型
    コツコツデータをまとめる
  • 分割型
    順次クラスタを分割する

AgglomerativeClusteringをimportする。