🗻
微分と勾配法
目的
- 数学ダメダメの自分が「ゼロから作るDeep Lerning」を読んで勾配降下法について学んだのでまとめます。
- 詳細を忘れたときに見返せるようメモします。
- 私のように「ゼロから作るDeep Lerning」を読んで「数学わからん!!」となった人の助けになればと思います。
- 最大限注意をして、この記事を作成していますが、誤りがありましたらご指摘いただけると幸いです。
勾配法(こうばいほう)とは
- 最適化問題などで
最大もしくは最小の値を探索するための手法です。 - 機械学習やディープラーニングでは最適なパラメータを探索するため使用します。
-
微分を使用し、各地点の関数の傾きを算出し傾斜が0になる点へ移動を繰り返すことで最小値を見つけます。 - 形が複雑で傾斜が0になる点が複数存在する関数の場合、必ずしも最小値を見つけられるわけではありません。
- そのため、平らな土地に入って学習が進まないプラトー現象に陥ることがあります。
微分とは
- 特定のタイミングの変化率(傾斜)を導くことができる手法?が
微分です。 - 関数に対する引数の値を固定し傾きを求めた物を
微分係数と言います。 - 引数を固定せず傾きを求める式を求めたものを
導関数と言います。 - 微分係数の数式は以下のように定義されます。導関数も同じ公式で導くことができます。
微分する(導関数を求める)
x^2
Pythonを使って微分する
数学では0に近い数値を定義できますが、
pythonでは1e-4(1*0.00001)という数値を使用します。
このような具体的な数値を使用して微分する方法を数値微分と言います。
すべての処理のソースコードは以下Githubをご確認ください。
関数を定義(x^2)
def function(x):
return (x**2)
微分公式
def numerical_diff(f, a):
h = 1e-4
return (f(a+h) - f(h) / (h))
微分の接線を求める公式
接線を求める
def tangent(function, x, a):
return numerical_diff(function, a) * (x - a) + function(a)
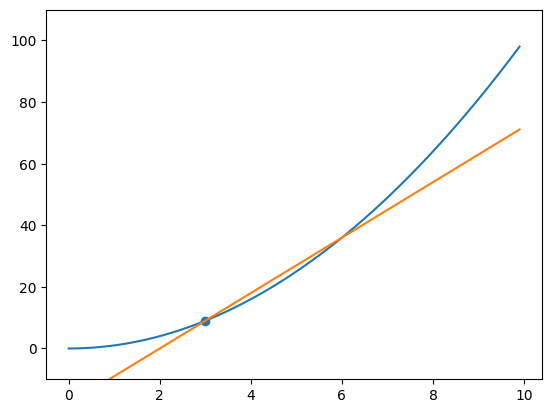
グラフに描画
a = 3
x = np.arange(0.0, 10.0, 0.1)
y = function(x)
plt.plot(x, y)
tangent_y = tangent(function, x, a)
plt.plot(x, tangent_y)
plt.scatter(a, numerical_diff(function, a))
plt.ylim(-10, 110)
plt.show()
偏微分とは
- 偏微分は複数変数を持つ関数において、一部の変数に着目し、その他の変数を定数扱いして微分する手法です。
- 微分は
変化率を導き出すための計算のため定数は微分の計算に影響しません。 - そのため一部のパラメータを固定し、確認したいパラメータの変化量を調べるということが可能になります。
偏微分する
x^2+y^2
yを定数扱いし、xで微分します。べき乗関数の微分公式(※1)より以下となります。
xを定数扱いし、yで微分します。
4x^2+4xy+2y^2+5
yを定数扱いし、xで微分します。
そのため以下のようになります。
xを定数扱いし、yで微分します。
Pythonを使って偏微分する
すべての処理のソースコードは以下Githubをご確認ください。
ループ処理の関係で配列を使用し
変数名が違うだけで上記で手計算した
関数を定義(x0^2+x1^2)
def function_2(x):
return x[0]**2 + x[1]**2
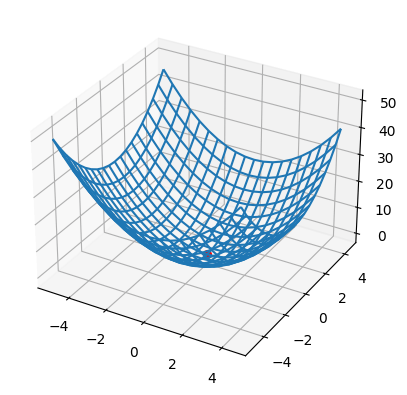
関数を描画する
x = np.arange(-5, 5, 0.5)
X,Y = np.meshgrid(x,x)
z = function_2(np.array([X, Y]))
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_wireframe(X, Y, z, zorder=1)
ax.scatter(0, 0, 0, s=30, c="red", zorder=2)
plt.show()
偏微分
def numerical_diff2(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
# x0 + h または x1 + hの値を割り出してx配列に戻す
x[idx] = tmp_val + h
# f(x0+h, x1)または(x0, x1+h)の値を求める
fxh1 = f(x)
x[idx] = tmp_val
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / h
# 次の微分計算のために+hした値から元の値に戻す。
x[idx] = tmp_val
return grad
勾配法の具体的な処理の流れ
勾配法は以下の流れで処理を実施します。
- 初期値を設定します。
- 現在地の勾配を計算します。
- 勾配が最小となる方向へ移動します。
- 移動した場所で再度勾配を計算します。
- この行程を指定回数繰り返します。
勾配法の計算式は以下です。
単一パラメータの勾配法
勾配法1
def gradient(f):
x = np.random.randint(8, 10, dtype='int')
study = 0.08
result = []
for i in range(15):
x = x - study * numerical_diff(f, x)
result.append(x)
return result
グラフ描画
a_list = gradient(function)
ax =[]
x = []
y = []
fig = plt.figure(dpi=400)
for i in range(len(a_list)):
ax.append(fig.add_subplot(4,4,(i + 1)))
ax[i].set_ylim(-1, 10)
x.append(np.arange(0.0, 6.0, 0.1))
y.append(function(x[i]))
for i in range(len(a_list)):
ax[i].plot(x[i], y[i], linewidth=0.8)
tangent_y = tangent(function, x[i], a_list[i])
ax[i].plot(x[i], tangent_y, linewidth=0.5)
ax[i].scatter(a_list[i], numerical_diff(function, a_list[i]), s=1)
plt.tight_layout()
plt.show()
探索過程のGIF
x軸とy軸がぷるぷるしているのは私のGIF作成方法が雑だからです。味だと思ってください。
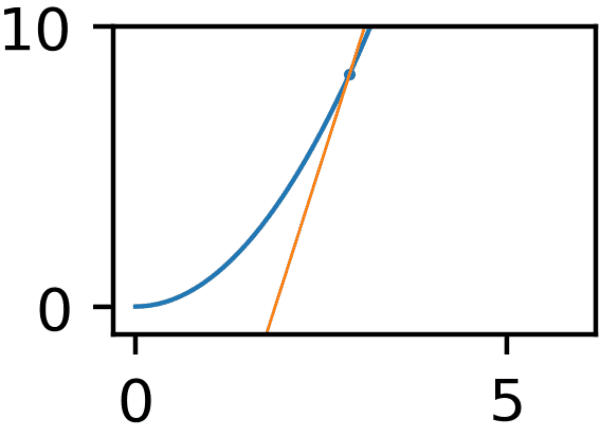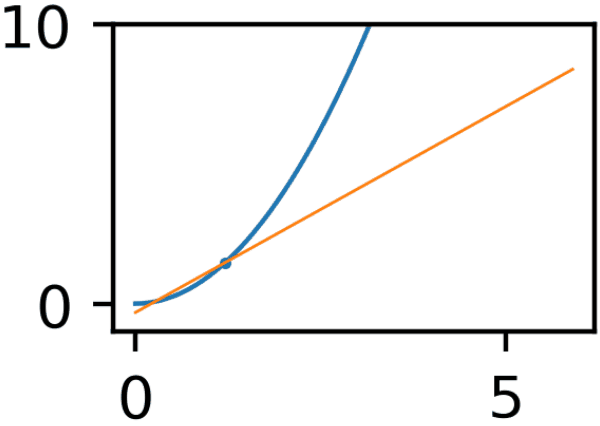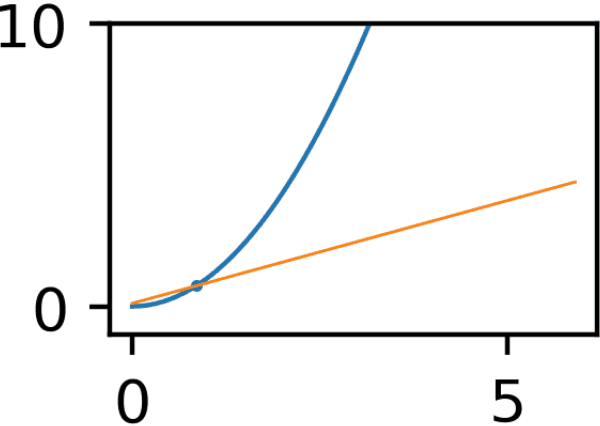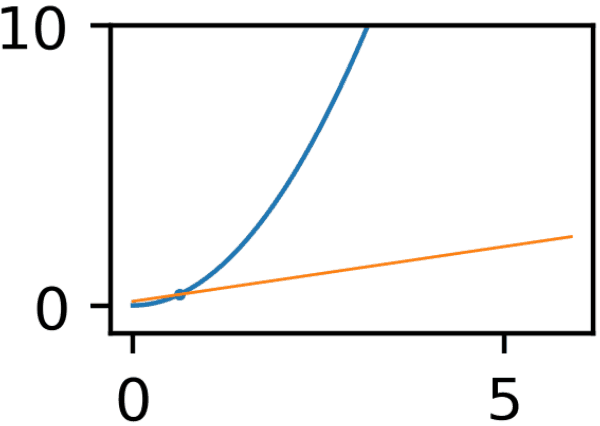
複数パラメータの勾配法
以下は偏微分をつかって複数パラメータで勾配法を行ったプログラムです。
勾配法2
def gradient_2(f):
x = np.array([np.random.randint(4, 6, dtype='int'),
np.random.randint(4, 6, dtype='int')])
study = 0.08
result = []
for i in range(15):
x = x - study * numerical_diff2(f, x)
result.append(x)
return result
gradient_2(function_2)
グラフ描画
x = np.arange(-5, 5, 0.5)
X,Y = np.meshgrid(x,x)
z = function_2(np.array([X, Y]))
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_wireframe(X, Y, z, zorder=1)
for v in gradient_2(function_2):
y = function_2(np.array([v[0], v[1]]))
ax.scatter(v[0], v[1], y, s=30, c="red", zorder=2)
plt.show()
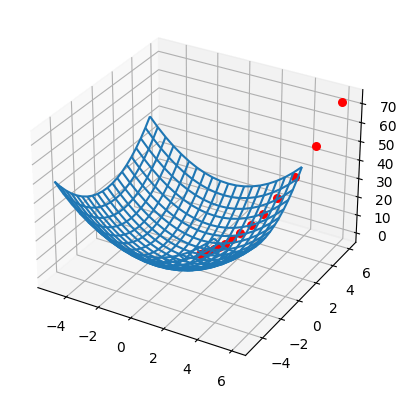
参考文献
- 斎藤康毅(さいとうこうき).ゼロから作るDeep Lerning-Pythonで学ぶディープラーニングの理論と実装.株式会社オライリー・ジャパン
- 小島寛之(こじまひろゆき).マンガでわかる微分積分.株式会社ビーコム
- 谷尻かおり.文系プログラマーのためのPythonで学び直す高校数学.日経BP社
Discussion