📉

Pythonで時系列分析し株価を予測できるか試してみる

2024/05/04に公開

Python

✅目的

今回はstatsmodelsを使用した統計的な時系列分析を行い株価の予測を行います。
時系列分析の基礎であるAR/MA/ARMA/ARIMAモデルについて解説し、ARIMA分析をS&P500の株価で実施し結果を確認します。
株価の当該手法による予測がどの程度意味があるのかわかりませんが、時系列分析の工程を整理する目的でこの記事を記述します。
時系列分析を行うにあたって確認する必要がある時系列データがランダムウォークかの判定方法や定常性の確認方法について記載します。
最終的な投資判断は自己責任となりますのでよろしくお願いします。
最大限注意をして、この記事を作成していますが、誤りがありましたらご指摘いただけると幸いです。

📃定常性とは

定常性とは時間経過にかかわらず平均、分散、自己相関が変化しない時系列データのことです。
例としては右肩上がりや右肩下がりの一定のトレンドを持つような株価の時系列データは定常と言えません。
統計的モデルの場合、過去の動きが一定でないと未来の予測がままならなくなってしまいます。
そのため、統計的モデルを使用した時系列分析では時系列データを加工し定常化する工程を実施する必要があることがあります。
1990年バブル崩壊後の日経平均7000円の状態から100円値上がりするのと現在の30000円後半の状態100円値上がりするので同じ100円でも話が違ってくるかと思います。
そのため、株価をそのまま分析するのではなく値上がり率などを使って分析する必要があるという話だと感覚的にわかりやすかもしれません。

📃定常化処理について

定常化の処理として単純なもので差分をとることで、平均を安定させることができます。
または、対数差分系列を使用することもあります。

差分
現在の時間ステップ $y_t$ から一つ前のステップ $y_{t-1}$ の値を引いて $y'_t$ を求めます。

y'_t = y_t - y_{t-1}

対数差分
現在の時間ステップ $y_t$ の対数から一つ前のステップ $y_{t-1}$ の対数の値を引いて $y'_t$ を求めます。

y'_t = log(y_t) - log(y_{t - 1}) = log(\frac{y_t}{y_{t-1}})

🐍Pythonによる定常化処理実装と定常性確認

SP500の株価を取得
pandas datareaderでsp500の株価を取得します。
sp500の株価を定常化処理を行います。

import pandas as pd
import numpy as np
import pandas_datareader.data as web
from itertools import product

import datetime
import matplotlib.pyplot as plt

#取得するデータの開始日と最終日を指定
start = datetime.datetime(2020, 1, 1)
end = datetime.datetime(2024, 5, 1)

eq = web.DataReader('sp500', 'fred', start, end)

差分取得処理

eq_diff = np.diff(eq['sp500'], n=1)

対数差分取得処理

eq_log_diff = np.log(eq['sp500']).diff(1)

# nanが含まれる行を削除する
eq_diff_log = eq_diff_log.dropna(how='all')

グラフを表示
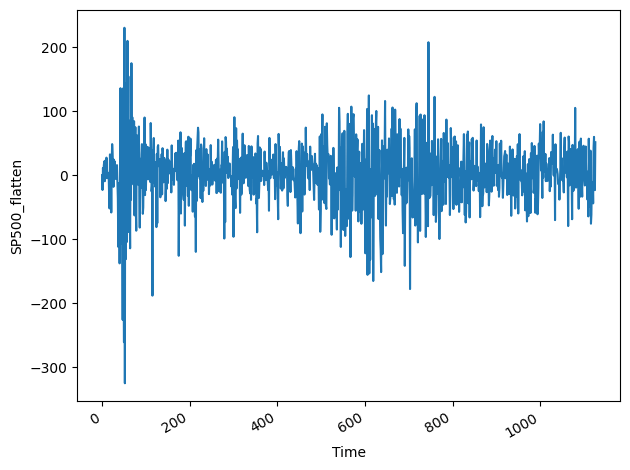
以下、差分処理後の時系列をグラフで表示してみます。

fig, ax = plt.subplots()

ax.plot(eq_diff)
ax.set_xlabel('Time')
ax.set_ylabel('SP500_flatten')

fig.autofmt_xdate()
plt.tight_layout()

ビジュアル的に0を基準に分散が一定になっていることがわかるかと思います。

ADF(拡張ディッキーフラー)検定による定常性確認
ADF検定は単位根検定の一つで、時系列データが定常過程であるかどうかを検定するのに使用します。
p値が有意水準以下であればデータが定常であると判断します。
有意水準は0.05未満であれば帰無仮説を棄却することができ、定常系列であると判断できます。

差分取得処理後のデータをADF検定する。

from statsmodels.tsa.stattools import adfuller

ad_fuller_result = adfuller(eq_diff)

print(f'ADF Statistic: {ad_fuller_result[0]}')
print(f'p-value: {ad_fuller_result[1]}')

実行結果
以下の結果はp値はp-value: 1.1201597517131986e-17のため0.05以下であるため定常系列と判断できます。

📃ランダムウォーク

ランダムウォークとは各ステップが乱数分だけ等確率で上昇または下降する時系列のことです。
式で表すと以下となります。
$y_{t}$ は現在の値で $y_{t-1}$ は一つ目のステップです。 $ε_t$ はホワイトノイズです。
$C$ は定数項です。モデルの当てはまりをよくするための切片です。
また、市場のトレンドを表現するためにドラフト項として $δ$ を項に追加する式もあります。

y_t = C + y_{t-1} + ε_t

ホワイトノイズとはどのタイミングでも平均が0で、自己相関を持たない乱数です。
上記式は定数項を無視すればホワイトノイズをステップごとの累積和であることがわかります。
そのためランダムウォークな時系列データは自己相関を持たず、過去のステップから未来のステップを予測することは不可能と言われています。

🐍Pythonによる時系列データのランダムウォーク判定

ランダムウォークは自己相関を持たないためACFプロットを使って自己相関を確認することができます。
SP500の株価を定常化した後、ACFプロットで自己相関を確認できます。

from statsmodels.graphics.tsaplots import plot_acf
plot_acf(eq_diff, lags=30)
plt.tight_layout()

コレログラムは自己相関を確認するためのグラフです。
x軸はラグを、y軸は相関係数を表します。そのためラグ0の相関は1となっています。
相関係数0周りに表示されている青い長方形は有意水準を荒らしています。
このグラフの結果をみるにぽつぽつと有意水準を超えるラグも存在しなんとも微妙ですが、わかりやすい自己相関はないのではと判断します。
そのため、SP500の株価はほぼほぼランダムウォークであるのではないかと推測できます。

📃AR(自己回帰|Auto Regressive)

AR過程は過去の現在の値を過去のデータを用いて回帰し説明するモデルです。
過去の複数ステップごとの値と自己相関係数をもとに回帰分析しデータにフィットさせることで推定を行います。
自己相関Φが1に近いほど、現在の時点の値と直近の過去の値との間に強い相関があることを示し、過去の値が未来の値を予測するのに役立つことを意味します。

1次のAR過程
1次前までの自己相関がある時系列データの場合のAR式は以下となります。
$Φ_1$ は自己相関係数で、 $ε_t$ は現在のホワイトノイズ、 $ε_t-n$ は過去のホワイトノイズです。

y_t=C+Φ_1y_{t-1}+ε_t

p次のAR過程
$p$ は過去のステップをどこまで振り返るかによって値が決定します。

y_t=C+ε_t+Φ_1y_{t-1}+Φ_2y{t-2}+・・・+Φ_py_{t-p}

📃MA(移動平均|Moving Average)

MA過程はホワイトノイズを拡張したもので、ホワイトノイズの線形和で表すモデルです。
過去のホワイトノイズの値とそれに対応する係数によって式が構成されています。

1次のMA過程
μは時系列の平均、ε_tは現在のホワイトノイズ、 $ε_t-n$ は過去のホワイトノイズです。
$θ$ は過去のホワイトノイズが現在のホワイトノイズにどの程度影響を与えるかの係数です。この係数は最小二乗法や最尤推定などにより決定します。

y_t = μ + ε_t + θ_1ε_{t-1}

q次のMA過程
$q$ は過去のステップをどこまで振り返るかによって値が決定します。

y_t = μ + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2}+ ・・・ + θ_qε_{t-q}

📃ARMA(自己回帰移動平均|Auto Regressive Moving Average)

ARMA過程はAR過程とMA過程の組み合わせたモデルです。
ARとMAの性質を併せ持っており、両モデルのうち強いほうがARMAモデルの性質となります。

p,q次のARMA過程
ARの式とMAの式を結合した式となっています。

y_t = C+ε_t+Φ_1y_{t-1}+Φ_2y{t-2}+・・・+Φ_py_{t-p} + μ + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2}+ ・・・ + θ_qε_{t-q}

📃ARIMA(自己回帰和分移動平均|AutoRegressive Integrated Moving Average)

ARIMA過程はAR(p)過程、和分(d)、MA(q)過程の組み合わせです。
ARIMA過程はデータが定常でなくても使用することができます。

ARIMA(p,d,q)次のARIMA過程
$y_t$ で表される元の時系列を使う代わりに、 $y'_t$ で表される差分時系列を使用します。
$d$ は差分をとる回数を表していて、定常化するまでの差分取得回数を表しています。

y'_t = C+ε_t+Φ_1y'_{t-1}+Φ_2y'{t-2}+・・・+Φ_py'_{t-p} + μ + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2}+ ・・・ + θ_qε_{t-q}

📃処理の流れ

pandas_datareaderでS&P500の株価を取得します。
interpolate()を使って休日や祝日などnanの株価を補完します。
statsmodelsを使い株価のトレンド,季節性,残差を確認します。
対数差分による定常化を行いADF検定で定常化されたことを確認します。
AIC(赤池情報量基準)を用いて次数(p,q)を最尤推定により選択します。
定常化実施回数の次数dと推定した次数(p,q)パラメータを設定し、テストデータを細切れにしステップごとに次のステップの株価を予測します。
二乗平均平方根誤差(RMSE)で予測精度を確認します。
直近の株価から未来の株価を予測します。

🐍Pythonで実行してみる

実行はGoogle Colaboratoryを使用しました。
全処理内容は以下を参照してください。

pandas_datareaderでS&P500の株価を取得

pandas_datareaderを使ってS&P500の株価を取得します。
この記事を記述しているのは2024/5/4なので現在の株価まで取得したいため5日を指定しています。

#取得するデータの開始日と最終日を指定
start = datetime.datetime(2020, 1, 1)
end = datetime.datetime(2024, 5, 5)

株価の取得およびNaNが含まれているかの確認を行っています。
また、後続処理でwarningが出るためfreqの設定をしています。

eq = web.DataReader('sp500', 'fred', start, end)
print(eq.index)

## データにNaNの数を確認
print(eq.isnull().sum())

## 取得したdataframeにfreqを設定
eq.index.freq = 'B'
print(eq.index)

interpolate()を使って休日や祝日などnanの株価を補完

eq = eq.interpolate(limit=1, limit_direction='both')
eq

statsmodelsを使い株価のトレンド,季節性,残差を確認

時系列データをトレンド,季節性,残差に分解しています。
引数であるperiod=30は周期を表しており1ヶ月周期で確認を行っています。

from statsmodels.tsa.seasonal import seasonal_decompose, STL
advanced_decomposition = STL(eq.sp500, period=30).fit()

fig, (ax1, ax2, ax3, ax4) = plt.subplots(nrows=4, ncols=1, sharex=True)

ax1.plot(advanced_decomposition.observed)
ax1.set_ylabel('元データ')

ax2.plot(advanced_decomposition.trend)
ax2.set_ylabel('トレンド')

ax3.plot(advanced_decomposition.seasonal)
ax3.set_ylabel('季節性')

ax4.plot(advanced_decomposition.resid)
ax4.set_ylabel('残差')


fig.autofmt_xdate()
plt.tight_layout()

季節性のグラフを確認すると年末および年始にボラティリティが上がっていることが多いように見えなくもないです。
アノマリーとしてよく言われるクリスマスラリーや1月効果などはあながち間違いではないのかもしれません。

対数差分による定常化を行いADF検定で定常化されたことを確認

ここの処理は上記、定常化の説明と同じなため省略します。

AIC(赤池情報量基準)を用いて次数(p,q)を推定

AIC(赤池情報量基準)とは統計モデルの良さを評価するための指標です。
値が小さいほど当てはまりが良いという判断ができます。
今回、当てはまりのよい次数(p,q)をAICを使用して調べます。
p,qの0~3までの次数の組み合わせタプルを作成し実際にARIMAモデルを作成した結果からAICの値を取得します。

from statsmodels.tsa.statespace.sarimax import SARIMAX
from tqdm import tqdm_notebook
from typing import Union

def optimize_ARIMA(data, order_list, d):
  results = []

  for order in order_list:
    try:
      model = SARIMAX(data, order=(order[0], d, order[1]), freq='B').fit(disp=False)
    except:
      continue

    aic = model.aic
    results.append([order, aic])

  result_df = pd.DataFrame(results)
  result_df.columns = ['(p,q)', 'AIC']

  return result_df

ps = range(0, 4, 1)
qs = range(0, 4, 1)
d = 1

order_list = list(product(ps, qs))

train = eq['sp500'][:-300]

result_df = optimize_ARIMA(train, order_list, d)
result_df.sort_values(by='AIC')

探索結果からAICが最小である(p=2,q=2)を選択します。

テストデータのステップごとの株価の予測

テストデータをwindowサイズごとにループします。
前のステップのwindowサイズで指定した日数をもとに次のwindowサイズ日数分予測を行います。
この処理をテストデータ分繰り返します。

## テストデータの株価を指定日数ごとに分けて小分けに予測する。
def rolling_forecast(df, train_len, test_len, window, p, d, q):

    total_len = train_len + test_len

    pred_ARMA = []

    ## トレーニングデータ以降を始点としてテストデータをwindowで指定した数ごとに分けてループする。
    for i in range(train_len, total_len, window):
      model = SARIMAX(df[:i], order=(p,d,q))
      res = model.fit(disp=False)
      predictions = res.get_prediction(0, i + window - 1)
      oos_pred = predictions.predicted_mean.iloc[-window:]
      pred_ARMA.extend(oos_pred)

    return pred_ARMA

# テストデータを取得
test = eq['sp500'][-300:]
 
TRAIN_LEN = len(train)
TEST_LEN = len(test)

# 3日ごとに予測 
WINDOW = 3
# 次元p,qはAICで調べた値を代入 
P = 2
Q = 2
# 次元d定常化を実施した回数を代入
D = 1

pred_ARIMA = rolling_forecast(eq, TRAIN_LEN, TEST_LEN, WINDOW, P, D, Q)

test = pd.DataFrame({'test': test})
test.loc[:, 'pred_ARIMA'] = pred_ARIMA

test

精度確認

グラフを表示してテストデータと予測データを描画します。
3日ごとのローリング予測であるためテストデータと予測データの乖離はあまり発生していないように見えます。
当たり前ですが、予測期間をのばせばのばすほど予測精度が悪くなります。
また、予測は過去の値動きをもとに行っていますので暴落を未然に検知することなどもできません。

fig, ax = plt.subplots()

ax.plot(train)
ax.plot(test['test'], 'b-', label='actual')
ax.plot(test['pred_ARIMA'], 'k--', label='ARIMA(2,1,2)')

ax.set_xlabel('Date')
ax.set_ylabel('SP500')

ax.legend(loc=2)

fig.autofmt_xdate()
plt.tight_layout()

rmseによる予測精度の確認を行っています。
この値が小さければ実際の値と予測値との誤差が少なくよいモデルと言えます。

from sklearn.metrics import mean_squared_error
from math import sqrt
rmse_ARIMA = sqrt(mean_squared_error(test['test'], test['pred_ARIMA']))

print(rmse_ARIMA)

結果としては48.70...ということで誤差49ドル前後で予測できているようです。

未来の株価の予測

直近の株価をもとに未来9日間の株価を予測してみます。

test = eq['sp500'][-300:]

# 直近の株価(テストデータで使用した株価)をもとに未来9日の株価を予測する。
TRAIN_LEN = len(test)
FORECAST = 9

# 3日ごとに予測をする。
WINDOW=3

forecast_ARIMA = rolling_forecast(test, TRAIN_LEN, FORECAST, WINDOW, P, D, Q)

米国市場が開いていた2024/5/3(金)のS&P500の終値が5127.80ドルということで以下予測も5000ドル前半のレンジでウロウロする予測となっています。
人間が予想する株価の感覚から大きく乖離していないため正常に予測できていると判断します。

📃まとめ

今回、統計的な手法を用いた時系列分析についてまとめました。
時系列分析を行う上で重要な定常性やランダムウォークについて記載しました。
時系列分析の基礎であるAR/MA/ARMA/ARIMAモデルについて解説し、ARIMA分析をS&P500の株価で実施し、未来の株価を予測しました。

📃参考文献

沖本竜義.経済・ファイナンスデータの統計時系列分析.朝倉書店
Marco Peixerio.Pythonによる時系列予測(Compass Booksシリーズ).マイナビブックス
Satoshi A.時系列分析(統計モデル編).Udemy

✅目的