📐
単回帰分析をわかりやすく説明してみる
✅目的
- 数学ダメダメの自分が回帰分析を学んだのでまとめておこうと思います。
- 詳細を忘れたときに見返せるようメモします。
- 可能な限り平易に説明することを目指します。私のように完全独学で勉強している人の助けになればうれしいです。
- 最大限注意をして、この記事を作成していますが、誤りがありましたらご指摘いただけると幸いです。
📃回帰分析(かいきぶんせき)とは
- 回帰分析は結果となる数値と要因となる数値の関係を調べる分析手法です。
- 回帰分析は
単回帰分析や重回帰分析など複数種類が存在する回帰分析の総称です。- 1つの変数から結果との関係を導き出す回帰分析を
単回帰分析と呼びます。 - 複数変数から結果との関係を導き出す回帰分析を
重回帰分析と呼びます。
- 1つの変数から結果との関係を導き出す回帰分析を
- データの結果となる変数を
目的変数データの結果の要因となる変数を説明変数と言います。 - 単回帰分析の場合、
目的変数をy軸に,説明変数をx軸に散布図としてプロットし、回帰直線を引くことで分析することができます。
📃単回帰分析でできること
単回帰分析でわかることは以下がわかります。
-
因果関係の推定
説明変数xは目的変数yにどの程度影響があるのか定量的に把握することができます。 -
予測
目的変数yが未知のときに、説明変数xのデータが存在すれば目的変数yを予測することができます。
📃具体的な単回帰分析の方法
- 相関があると思われる目的変数と説明変数を複数用意します。
今回は「身長が高ければ体重も重い」という憶測をもとに以下データを集めたとします。
| 身長y(cm) | 体重x(Kg) |
|---|---|
| 170 | 60 |
| 165 | 55 |
| 182 | 80 |
| 172 | 65 |
| 168 | 52 |
| 155 | 50 |
| 150 | 45 |
| 175 | 80 |
| 178 | 60 |
| 166 | 53 |
-
取得したデータをもとに散布図を作成します。
以下の散布はx軸に体重をy軸に身長をあてはめてプロットしった散布図です。
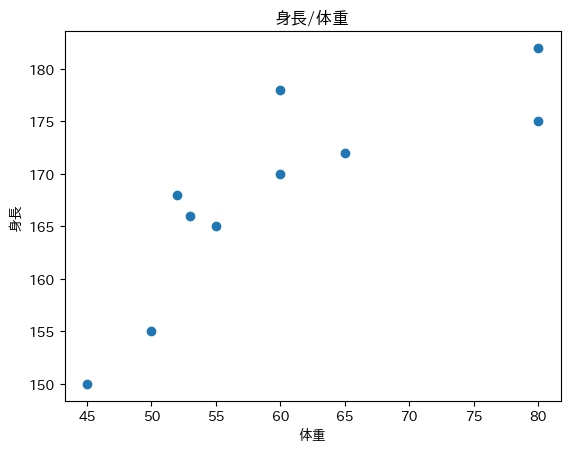
-
分散、共分散または標準偏差、相関係数を求めます。分散と共分散を求める式は以下です。
分散
標準偏差
共分散
相関係数
- 以下の式をもとに傾きaと切片bを求めます。
💬コラム:なぜ、分散と共分散から回帰直線が引けるの?
1次関数の回帰直線がなぜ共分散と分散で近似できるのかは
最小二乗法を計算することで説明することができます。
詳細については別記事にまとめていますので興味がありましたらご参照ください。
- 計算結果をもとにy=ax+bの1次式を描画します。
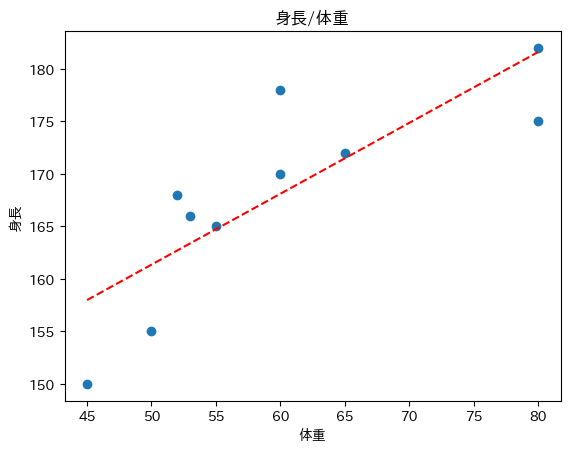
🐍pythonで回帰直線を求める
フルスクラッチ、numpy、sklearnそれぞれの回帰分析の方法を紹介します。
やっていることはすべて同じです。全ソース確認したい場合は以下を参照ください。
計算式をもとに回帰直線を求める
標準偏差を求める
標準偏差を求める(1)
## x標準偏差
x = body_df['体重']
x_mean = x.mean()
tmp = (x - x_mean) ** 2
std_x = tmp.sum() / x.shape[0]
std_x = std_x ** 0.5
以下はpandasを使って標準偏差を求める方法です。
今回は標本分散を使用した標準偏差を求めるためddof=0を引数に指定します。
標準偏差を求める(2)
x.std(ddof=0)
共分散を求める
共分散を求める(1)
## 共分散
tmp = (x - x_mean) * (y - y_mean)
cov = tmp.sum() / len(tmp)
以下はnumpyを使って共分散を求める方法です。
共分散を求める(2)
np.cov(x, y, bias=True)
相関係数を求める
相関係数を求める(1)
r = cov / (std_x * std_y)
以下はpandasを使って相関係数を求める方法です。
相関係数を求める(2)
body_df.corr()
傾きを求める
以下は分散と共分散から傾きを求めています。
分散と共分散から傾きを求める。
# 傾きa(共分散と分散を使った求め方)
reg_a = cov / x.var(ddof=0)
reg_a
以下は相関係数と標準偏差から傾きを求めています。
相関係数と標準偏差から傾きを求める。
# 傾きa(相関係数と標準偏差を使った求め方)
reg_a = r * (std_y / std_x)
reg_a
切片を求める
reg_b = y_mean - (reg_a * x_mean)
reg_b
回帰直線を描画する。
fig, ax = plt.subplots()
line_x = np.linspace(x.min(), x.max())
line_y = reg_a * line_x + reg_b
ax.set_title("身長/体重")
ax.set_xlabel("体重")
ax.set_ylabel("身長")
ax.plot(line_x, line_y, color='Red')
ax.scatter(body_df['体重'], body_df['身長'], marker='o')
plt.show()

numpyを使って回帰直線を求める
傾きと切片を求める
reg = np.polyfit(x, y, deg=1)
回帰直線を描画
fig, ax = plt.subplots()
line_x = np.linspace(x.min(), x.max())
line_y = reg[0] * line_x + reg[1]
ax.set_title("numpyのpolyfitで回帰直線を描画")
ax.set_xlabel("体重")
ax.set_ylabel("身長")
ax.plot(line_x, line_y, color='Red')
ax.scatter(body_df['体重'], body_df['身長'], marker='o')
plt.show()
描画結果

sklearnを使った回帰直線を求める
傾きと切片を求める
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
X = x.values.reshape(-1, 1)
y = y.values.reshape(-1, 1)
reg.fit(X, y)
print('a = ', reg.coef_)
print('b = ', reg.intercept_)
回帰直線を描画
fig, ax = plt.subplots()
line_x = np.linspace(x.min(), x.max())
line_y = reg.coef_[0] * line_x + reg.intercept_[0]
ax.set_title("sklearnで回帰直線を描画")
ax.set_xlabel("体重")
ax.set_ylabel("身長")
ax.plot(line_x, line_y, color='Red')
ax.scatter(body_df['体重'], body_df['身長'], marker='o')
plt.show()
描画結果

参考文献
- 向後 千春/冨永 敦子.統計学がわかる【回帰分析・因子分析編】ファーストブック.技術評論社
- 杉山聡.本質を捉えたデータ分析のための分析モデル入門.ソシム
Discussion