🙈
クウォータ二オン(四元数)を理解したいメモ

2022/08/27に公開
 はじめにCG系のソフトウェアを使っていると回転周りでクウォータ二オンがでてくるが何となくの概要の理解だけで、いつかちゃんと理解したいなぁと思いつつ逃げてきた。

重い腰を少しあげれたのでそれをメモする。

 モチベーション
 自分たちのモチベーションxyzの三次元空間を扱うCGにおいての回転を表現する方法で一番最初に思いつくのがオイラー角による回転表現がある。
こんな直交座標系があったとして、



初期姿勢 
 引用画像 https://www.sky-engin.jp/blog/eulerian-angles/
各軸に〇〇度回転みたいなことを考えて回転を表現する方法。


オイラー角 
 引用画像 https://www.sky-engin.jp/blog/eulerian-angles/
こうすれば、任意の角度の姿勢を表現することができそうって思いつく。

シンプル。
オイラー角を簡単に体験できるものを作ってた人がいたので共有。

https://www.sky-engin.jp/EulerianAnglesTool/eulerian-angles-tool.php?lang=ja
このオイラー角をソフトウェア上で実装することを考えると、具体的には回転行列みたいなものを考えてその軸にたいしての回転行列の積をとってあげる。みたいなイメージ
Rx(θ)=
\begin{bmatrix}
1 & 0 & 0 \\
0 & cosθ & −sinθ \\
0 & sinθ & cosθ \\
\end{bmatrix}, 
Ry(θ)=
\begin{bmatrix}
cosθ & 0 & sinθ \\
0 & 1 & 0 \\
-sinθ & 0 & cosθ \\
\end{bmatrix}, 
Rz(θ)=
\begin{bmatrix}
cosθ & -sinθ & 0 \\
sinθ & cosθ & 0 \\
0 & 0 & 1\\
\end{bmatrix}
行列で計算しているのなら積の順序が大切になってくる、どの軸の回転から先に計算するかによっても結果がことなってくる。

その行列の積の一環で問題にぶち当たることがある。
有名なぶち当たる問題点として、ジンバルロックという現象がある。

それは回転が一見して効かなくなったり、おかしくなったりして

回転に関わるアニメーションがうまく適用できなかったりする現象。
このジンバルロックを解決させる策が、四元数、クウォータ二オンを使った回転方法である。

この概念を理解できれば、あらゆるCGソフトウェアでも一貫して使える知識のため役に立つため、クウォータ二オンを知りたい！

 ジンバルロックジンバルロックの状態を具体的なイメージで説明してくれている動画。

https://youtu.be/zc8b2Jo7mno
簡単に説明すると、ある特定の条件の時に、他2軸の値を変更しても見た目上同一方向の回転に見えてしまうということ。


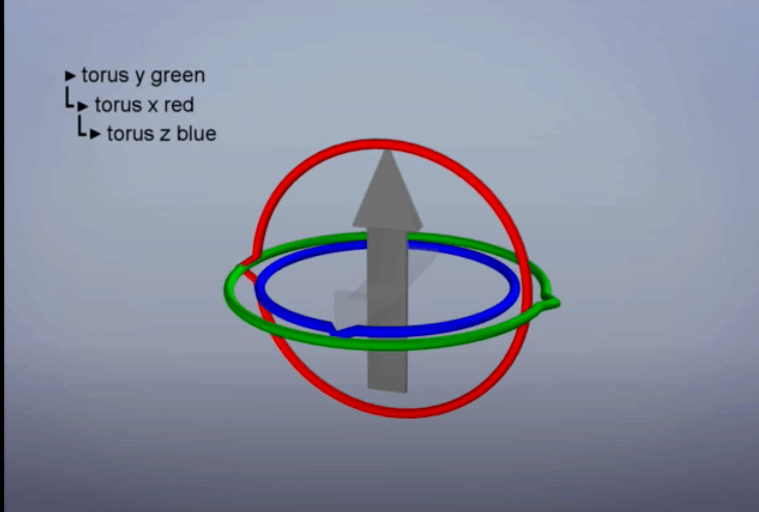
Euler (gimbal lock) Explained

 ジンバルロックの運用上での回避方法Mayaを使った例で、実際どのように回避しているかを説明してくれている人がいた。

https://www.youtube.com/watch?v=oXy8wn1qeN0

上は運用上での避け方であって、

根本的な解決ではない

 その他のオイラー角における問題点その他のオイラー角における問題点について、具体例で示してくれいている人がいたので貼っておく。
https://docs.godotengine.org/ja/stable/tutorials/3d/using_transforms.html

 自分たちのモチベーション Referencehttps://bluebirdofoz.hatenablog.com/entry/2021/09/16/041442
http://akasuku.blog.jp/archives/54477982.html
https://www.youtube.com/watch?v=oXy8wn1qeN0
https://youtu.be/zc8b2Jo7mno
https://qiita.com/fullmated/items/ac62ebd1206a6487232d
https://tokoik.github.io/gg/ggbook03.pdf
https://docs.godotengine.org/ja/stable/tutorials/3d/using_transforms.html
https://www.sky-engin.jp/blog/eulerian-angles/
https://risalc.info/src/euler-angle.html
https://qiita.com/take4eng/items/0f5a9ff47fd345e5fc33

 数学的なモチベーション複素数を拡張した数を考えよう とすることから生まれた数体系。

名前だけよく聞くハミルトンさんが思いついた数体系らしい。
ハミルトンは複素数が座標平面における点として解釈できることを知っていて、三次元空間の点に対して同じことができる方法を探していた。空間の点はそれらの座標としての数の三つ組によって表すことができ、ハミルトンはそれらの三つ組に対して加法や減法をどのようにすべきかはずっと前から分かっていたのだが、乗法と除法をどう定めるかという問題については長く行き詰ったままであった。ハミルトンは、空間における二点の座標の商をどのように計算すべきかを形にすることができなかったのである。
四元数についての大きな転換点がついに訪れたのは、1843年10月16日の月曜日、ダブリンにおいてハミルトンが理事会の長を務めることになるアイルランド王立アカデミー（英語版）への道すがら、妻とともにロイヤル運河（英語版）の引き船道に沿って歩いているときであった。四元数の背景となる概念が頭の中で形になり、答えが明らかになったとき、ハミルトンは衝動を抑えられずに、四元数の基本公式
{\displaystyle i^{2}=j^{2}=k^{2}=ijk=-1}i^2 = j^2 = k^2 = ijk = -1を、渡っていたブルーム橋（英語版）の石に刻みつけた。

[引用]　https://ja.wikipedia.org/wiki/四元数
要約すると、複素数が二次元平面座標を表すことができるなら 、

三次元空間座標を複素数的な数を使って表すことができるんじゃないか？ というモチベーションだったらしい。

ただ、後にベクトル解析の方が表現するのに便利だねという意見が強まり、数学・物理界においては勢力が弱まってきたが、後の時代にCGやCV(コンピュータビジョン)などにおいて便利なことに気づかれたよう。
四元数は20世紀の後半になって、三次元の自由な回転を記述する能力を買われて、多用されることとなった。四元数による3次元の回転（姿勢）の表現は、3次正方行列による表現と比べて記憶容量が小さくて演算のスピードも速い。加えて、オイラー角と違ってジンバルロックが起きない。この特徴は、地上における上下方向のような絶対的な軸の無い、宇宙機のような三次元の自由度が完全にある場合の姿勢制御などでの利用に適しており[11]、宇宙機以外にもCG[12]、コンピュータビジョン、ロボット工学、制御理論、信号処理、物理学、生物情報学、分子動力学法、計算機シミュレーションおよび軌道力学など、他にも多くの応用がある。

[引用]　https://ja.wikipedia.org/wiki/四元数
元々は三元数っていうものがないかという風に考えた。

虚数単位を2個で、三次元空間を表せないか？という試みからスタートしたみたいだが、どうにもこうにも無理で試行錯誤した結果、3つならいける四元数というものにゴールした。

 数学的なモチベーション Referencehttps://ja.wikipedia.org/wiki/四元数

 四元数 クウォータ二オン集合としては、四元数全体 H は実数体上の4次元数ベクトル空間 ℝ4 に等しい。H には3 種類の演算（加法、スカラー乗法、四元数の乗法）が入る。H の二元の和は、ℝ4 の元としての和で定義され、同様に H の元の実数倍も ℝ4 におけるスカラー倍として定義される。H の二元の積を定めるには、まず ℝ4 の基底を決めなければならないが、その元を通例 1, i, j, k と記す。H の各元はこれら基底元の線型結合で表される。つまり
 a1 + bi + cj + dk の形に一意に表される。基底元 1 は H の乗法単位元であるため、通常省略して
 a + bi + cj + dkと表すのが普通である。

[引用]　https://ja.wikipedia.org/wiki/四元数
とりあえず、以下のような線形結合的なものを考えてみる。

x = x_0 + x_1i + x_2j + x_3k \qquad(x_0, x_1, x_2, x_3 : 実数)

ここまでは別に問題ない。

次が最大の肝になってきて、意味わからなくなって、何回も見て見ぬふりしてきたポイント。
i^2 = j^2 = k^2 = -1 i^2 = -1のiは所謂、虚数単位として馴染みのあるもので、これがj, kという風にも存在している。これらは全て二乗すると-1になるのだが、

それぞれは別々の変数であること が最大のポイント。

(\sqrt{\pm2})^2 = 2の +2と-2が別々の実数であるが、二乗した結果が同じように、

複素数の世界にもi以外に同様な、j, kがあってもいいし、そうした場合を考えてみようというのが今回の肝になる。

 三元数を考えてみるこのi, j, kを理解するには一歩戻って三元数というものを考えてみる。
以下の画像は複素数(二元数)のときの座標平面(複素平面)で、虚数単位iをかけると90度回転しているという風に幾何学的に理解することができる。


[引用画像]https://qiita.com/SotaAsai/items/a662c5f4675a1b8985f2
この複素数を拡張した体系を考えてみることにする。それは、実軸と虚軸に対して垂直な軸を考えて、以下のような条件が成り立つような虚数単位jを導入してみるということ。
j^2 = -1, j =  \sqrt{-1}, j \neq i ポイントはj \neq iということ。

実軸と虚軸と垂直な軸を考えてみると、そのjにjをかけると-1になるということは手前に伸びてくる軸に対しても回転する幾何学的な意味を持っているのじゃないかという風に理解することもできる。



[引用画像]https://qiita.com/SotaAsai/items/a662c5f4675a1b8985f2
これがもしあったら便利そう。こんな三元数を考えてみたらどうなるのか？とハミルトンは考えてみたが、

どうやらこの三元数では「乗法について閉じてない」ということがわかった。

閉じてる、閉じてないという用語は群論などで出てくるが、閉じているとは

三元数の乗法を考えて計算してみた結果、三元数に戻ってくるか？という意味とも言える。

こういった今後計算を考えていく上で便利な演算に対しての規則が三元数では足りてないという壁にぶち当たることとなった。

ただ、4元数となるkという存在を考えてみると演算に対して都合が良くなることがわかったため、kが導入された。
そのハミルトンが考えて行った思考プロセスについて説明してくれている人がいるので以下を参照。

https://qiita.com/SotaAsai/items/a662c5f4675a1b8985f2

 四元数の定義定義にまた戻る。
i^2 = j^2 = k^2 = -1 ij = -ji = k, jk = -kj = i, ki = -ik = j 注意点は ij \neq jiという点。四元数では乗法における交換法則が成り立たない ということ。

行列や群論を少し勉強しようとしたことある人ならなんとなく、この成り立たないという感覚は納得できると思う。実数と複素数だけの世界しか知らない人にとっては交換法則が成り立たない体系なんてあるの？と思うかもしれないが、全然ある。四元数においてもこういう条件をつけてあげないと他の現象が成り立たなくなってしまうということだ。
数学チックに表現すると

四元数全体の集合をHとすると、

H =\{ s + xi + yj + zk | s,x,y,z \in \mathbb{R} \}
となり、複素数の場合\mathbb{C}は\{ 1,i \}を基底とする実数体上の2次元ベクトル空間とするなら、四次元数の集合Hは\{ 1,i,j,k \}を基底とする実数体上の4次元ベクトル空間であるという。
またi, j, kは以下が成り立つ


\begin{align}
  &xij = k \\
  &ijk = K^2 \\
  & k^2 = -1より \\
  & \therefore ijk = -1 \\
\end{align}


 和と積の定義和

\begin{align}
 & (s1 +x_1 i + y_1 j + z_1 k) + (s2 + x_2 i + y_2 j + z_2 k) \\
 & = (s1 + s2) + (x_1 + x_2)i + (y_1 + y_2)j + (z_1 + z_2)k \\
\end{align}
積

\begin{align}
 & (s1 +x_1 i + y_1 j + z_1 k)(s2 + x_2 i + y_2 j + z_2 k) \\
 & = (s_1 s_2 - x_1 x_2 - y_1 y_2 -z_1 z_2) + (s_1 x_2 + s_2 x_1 + y_1 z2 - y_2 z_1)i \\
 & + (s_1 y_2 + s_2 y_1 -x_1 z_2 + x_2 z_1)j + (s_1 z_2 + s_2 z_1 + x_1 y_2 - x_2 y_1)k \\
\end{align}
なんだか積に関しては難しいように書かれているが、ただ、書き下しているだけである。

ij = -jiなどになる点さえ注意して、積の順序さえ崩さなければ同じような式が出来上がる。

実数で成り立っていた、展開公式なども積の交換法則が成り立たなくなると、連動して成り立たないこともあるので実数と同じように成り立つとは思わないこと。
四元数は略記 で描かれる表記もある。

四元数q = s+xi+yj+zkとすると q = (s,(x,y,z))またはq = (s,v)のように描かれる。ここでいうvはv = (x,y,z)を表している。
略記で記法するとシンプルになる。

\begin{align}
 &和 : (s_1, v1_) + (s_2, v_2) = (s_1 + s_2, v_1+v_2) \\
 &積 : (s_1, v_1)(s_2, v_2) = (s_1 - s_2 - v_1　\cdot　v_2, s_1 v_2 + s_2 v_1 +(v_1 \times v_2)) \\
& ただしここでは、v_1 \cdot v_2はベクトルの内積を表し、v_1　\times v_2は外積を表す。
\end{align}
実数や三次元ベクトルを次のような四次元数と同一視することとする。

\begin{align}
 &(s, 0)と実数sを同一視する。すなわち(s,0) = s \\
 &(0, 0)と実数0を同一視する。すなわち(0,0) = 0 \\
 &(1, 0)と実数1を同一視する。すなわち(1,0) = 1 \\
 &(0, v)と三次元ベクトルvをを同一視する。すなわち(0,v) = v \\
\end{align}
この(4)の(0, v)の形を純虚四次元数 (pure imaginary quaternion)と呼ばれる。
また以下の式も成り立つ。

\begin{align}
 &p + 0 = 0 + p \\
 &1p = p1 = p \\
 &p + q = q + p\\
 &(p + q) + r = p + (q + r)\\
 &(pq)r = p (qr)\\
 &p(q+r) = pq + pr, (p+q)r = pr + qr\\
 &pq = 0 p = 0または q = 0(零因子が存在しない)
\end{align}
ちなみに、

スカラー倍も成り立つ。

 共役の四元数共役の複素数てきなかんじの、四元数の共役の四元数も定義する。

q = (s,v) = s + xi + yj + zkを任意の四元数としたときに \\
\bar{q} = (s, -v) = s -xi -yj -zk \\
をqの共役の四元数とする。
性質

q \bar{q} = \bar{q} q = s^2 + |v^2|
となり、qが単位四元数(s^2 + |v^2| = 1となるような四元数q)ならば、

q \bar{q} = \bar{q} q = 1

 四元数の絶対値任意の四元数qに対して、

|q| = (q \bar{q})^(1/2) = (s^2 + |v|^2)^(1/2)
と定義して、これをqの絶対値と呼ぶ。とくに、|q| = 1、すなわちs^2 + |v|^2 = 1のときは先ほど出てきた、単位四元数と呼ばれる。

これは四次元ベクトルの長さ(ノルム)と捉えても大丈夫。

 四元数の逆数逆数とは演算の結果、単位元になるような数であるから、

積に関しての逆数を考える時、

実数では2 * (1/2) = 1(単位元)

複素数では乗法の単位元は1となっている。

零でない複素数z = a + biを考えると、|z|も零でない。すなわち、|z|^2 = a^2 + b^2 \neq 0となる。ここでzと共役の複素数\bar{z}の席を計算すると

z \bar{z} = (a+bi)(a-bi) = a^2 + b^2 = |z|^2
両辺を|z|^2で割ると

 \frac{(z \bar{z})}{(|z|^2)}  = 1
となるため、

z^` = \frac{\bar{z}}{|z|^2}
とおくと、
 z z^` = 1 となり、z^` は z の逆数であることがわかる。

z^{-1} = \frac{\bar{z}}{|z|^2}
これをもとにさ、零でない四元数の逆数を定義しようとする。

四元数による割り算はこの逆数を掛ける演算とする。
q \neq 0　ならば q　は積に関する逆数 q^{-1} をもつ、これを四元数の逆数と呼ぶ。

q^{-1} =\frac{\bar{q}}{|q|^2}

 四元数と回転四元数を使った回転表現を理解するには決して直感的ではないため、準備が必要である。

概要としては、

ベクトルpを単位ベクトルaまわりにθ回転する変換を考えたい時、

いい感じの単位四元数qを使って、 q^{`} = qpq^{-1}と表せれる。これが回転と結びつくのは全然直感的でないため、まずは、ロドリゲスの回転公式を使って、四元数と結びつけて成り立つことを見ていく。

 平行成分と直行成分eを単位ベクトル、vを零でない任意のベクトルとしたときに、

vは一般にeと平行な成分v_{\parallel}と直行する成分v_{\perp}に分解できる。

r = |v|とすると、v_{\parallel} = (r \cos \theta)e(単位ベクトルeとの射影をとっている)はeと平行な成分である。

ここで\thetaはeとvのなす角である。

内積の定義より、

\begin{align}
 & \cos \theta = \frac{e \cdot v}{|e||v|}\\
 & v_{\parallel} = r \frac{e \cdot v}{|e||v|}e = r\frac{e \cdot v}{1 * r}e = (e \cdot v)e \\

\end{align}
となるから、v_{\parallel} + v_{\perp} = vより

v_{\perp} = v - (e \cdot v)e
となる。v_{\parallel} \cdot v_{\perp}の内積を計算してみると

\begin{align}
 & v_{\parallel} \cdot v_{\perp} = (e \cdot v)e \cdot (v - (e \cdot v)e) \\
 & = (e \cdot v)^2 - (e \cdot v)^2e \cdot e \\
 & = (e \cdot v)^2 - (e \cdot v)^2|e|^2 \\
 & = 0 \\

\end{align}
直行していることがわかる。

同様に、u, vが任意のベクトルの時にvのuに平行な成分をv_{\parallel}と直行する成分v_{\perp}に分解することを考えると

e = \frac{u}{|u|}として同様に計算すればできる。

\begin{align}
 & v_{\parallel} = |v| \cos \theta \frac{u}{|u|}  = |v| \frac{(u \cdot v)}{|u||v|} \frac{u}{|u|}\\
 & = \frac{(u \cdot v)}{|u|^2}u = \frac{u \cdot v}{(u \cdot u)}u\\
 \\
 & v_{\perp} = v - \frac{(u \cdot v)}{(u \cdot u)}u \\

\end{align}

 直行する座標ベクトル空間内の同一平面上でない零でない3本のベクトルは基底ベクトルになる。つまり、空間内の任意のベクトルをkの3本のベクトルで表せるということ。

u, vは零ベクトルでなく、 |u| = 1かつ u \perp vを満たすとすると、このときwをw = u \times vで定義すると、当たり前だがu, v, wは直行して、空間内の基底となる。外積を使っていることから明らかである。あ

さらに v = -u \times wが成り立つ。

 ロドリゲスの回転公式外積による回転の公式と呼ばれるらしい。
任意の点P(位置ベクトルp)を、任意に与えられた単位位置ベクトルaのまわりに\theta回転した点をP^`とし、その位置ベクトルをp^`とすると

p^` = p + \sin \theta (a \times p) + (1-\cos \theta)a \times (a \times p)
となる。
イメージとして以下のような感じ。記号は違うが、nをa, rをp, r^`をp^`としたときの状態。


[引用] https://w3e.kanazawa-it.ac.jp/math/physics/category/physical_math/linear_algebra/henkan-tex.cgi?target=/math/physics/category/physical_math/linear_algebra/rodrigues_rotation_matrix.html
p^`をいきなりpとaベクトルで表すことを考えると難しいので、わかるところから探す。|a| = 1は条件からわかる。

p_{\perp}とp_{\parallel}もとりあえずわかる。このaとp_{\perp}から作られるa \times p_{\perp}も導出できる。

p^`をp_{\perp}, p_{\parallel}, a \times p_{\perp}で表すことを考える。

ここでは、p_{\parallel}をaと平行な方向とする。

まず p^` = p^`_{\perp}+ p^`_{\parallel}と分解できることから、p^`_{\perp}とp^`_{\parallel}をp_{\perp}, p_{\parallel}, a \times p_{\perp}で表すことを考える。
まず、回転軸上のベクトルは長さも方向も変化しないから、p^`_{\parallel} = p_{\parallel}なことはわかる。

また、|p^`_{\perp}| = |p_{\perp}|である。さらに|a| = 1と a{\perp}p_{\perp} より、

|a \times p_{\perp}| = |a||p_{\perp}|\sin{\frac{\pi}{2}} = |p_{\perp}| = |p^`_{\perp}|
が求めれられる。(外積の定義に従っただけ)

さらに、p^`_{\perp}に対して、ベクトルの分解を使うと

p^`_{\perp} = |p^`_{\perp}|\cos \theta \frac{p_{\perp}}{|p_{\perp}|} + |p^`_{\perp}| \sin \theta \frac{a \times p_{\perp}}{|a \times p_{\perp}|} = \cos \theta p_{\perp} + \sin \theta (a \times p_{\perp})
になることがわかる。



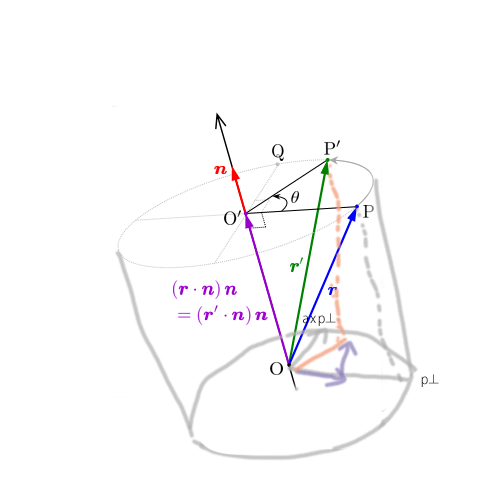
紫色がベクトルを分解したやつ
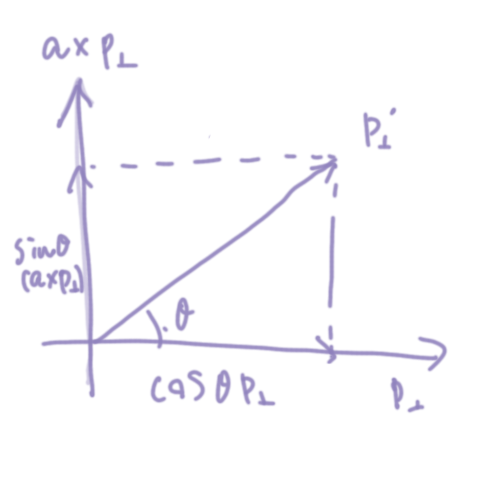
よって

p^` = p_{\parallel} + p^`_{\perp} = p_{\parallel} +\cos \theta p_{\perp} + \sin \theta (a \times p_{\perp})
となる。
上式の右辺をaとpで次は表すことを考える。

ここで、p_{\parallel} = p - p_{\perp}だから、代入すると

p^` = (p - p_{\perp}) +\cos \theta p_{\perp} + \sin \theta (a \times p_{\perp}) 
となり、よって、p_{\perp}がa , pで表せればok

ベクトル組{a, p_{\perp}, a \times p_{\perp}}を考えると、a \times p_{\perp}かつ|a| = 1だから、

p_{\perp} = -a \times (a \times p_{\perp})
が成り立つ。p = p_{\perp} + p_{\parallel}より、

a \times p = a \times p_{\perp} + a \times p_{\parallel}
で、p_{\parallel}はaに平行だから、外積の性質からa \times p_{\parallel} = 0となり

a \times p = a \times p_{\perp}
が成り立つため、

p_{\perp} = -a \times (a \times p)
となる。

よって全てを代入すると

\begin{align}
& p^` = (p - p_{\perp}) +\cos \theta p_{\perp} + \sin \theta (a \times p_{\perp}) \\ 
& = p + a \times (a \times p) - \cos \theta a \times (a \times p) + \sin \theta (a \times p) \\
& = p + \sin \theta (a \times p) + (1 - \cos \theta)a \times (a \times p) \\

\end{align}
よってロドリゲスの公式が証明された。
ベクトルの三重積の公式が含まれている式となっているのでさらに変形すると

※a \times (b \times c) = (a \cdot c)b - (a \cdot b)c : 三重積の公式

p^` = \cos p + \sin \theta (a \times p) + (1 - \cos \theta)(a \cdot p)a
が成り立つ。

ロドリゲスの回転公式は最終的なベクトルがどうであれ、幾何的理解より、回転を表していることは理解できる。

ここからqpq^{-1} = ロドリゲスの回転公式を見出すためにさらに準備する。

 単位四元数の角による表示以下を確かめていく。
任意の単位四元数qは適当な\thetaによって、q = (\cos \theta, \sin \theta a)と表せる。ここでのaは単位ベクトルとする。
仮定より、|q|^2 = s^2 + |v|^2 = 1 であり、|v|^2 \geq 0 より、s^2 \leq 1となる。したがって、-1 \leq s \leq 1となる。

適当な角\theta (0 \leq \theta \leq \pi)によって、s = \cos \thetaと表せれる。

これにより

|v|^2 = 1 - s^2 = 1 - \cos^2 \theta = \sin^2 \theta
となり、0 \leq \theta \leq \piで \sin \theta \geq 0だから |v| = \sin \thetaとなる。

一方、 v = |v| * \frac{v}{|v|}と書くことができて、a = \frac{v}{|v|}とおくと、aは単位ベクトルとなり、vはv = \sin \theta aと表せる。

よってq = (\cos \theta, \sin \theta a)となることがわかる。

 四元数の積3つの四元数の積を計算する。

任意の四元数をq = (s,v)p = (w, x)とする。

pを実数部分と純虚四元数に分けてp = (w, 0) + (0, x)と表せる。四元数を計算すると

qpq^{-1} = q((w, 0) + (0, x))q^{-1} = q(w,0)q^{-1} + q(0,x)q^{-1}
四元数qと実数wの積はwq = qwを満たす。これを四元数の形にすると、q(w, 0) = (w,0)qとなる

q(w, 0)q^{-1} = (w,0)qq^{-1} = (w,0)
さらに、q^{-1} = (\frac{1}{|q|^2})(s, -v)で\frac{1}{|q|^2}は実数だから上記と同じように

q(0,x)q^{-1} = \frac{1}{|q|^2}(s,v)(0,x)(s, -v)
右辺の3つの括弧の積を計算すると、

q(0,x)q^{-1} = (0, \frac{1}{|q|^2}\{(S^2 -V \cdot V)x + 2(x \cdot v)v - 2s(x \times v)\})
となり、qpq^{-1}にq(w, 0)q^{-1}, q(0,x)q^{-1}を代入すると、

\begin{align}

& qpq^{-1} = q(w,0)q^{-1} + q(0,x)q^{-1} \\
& = (w, \frac{1}{|q|^2}\{(S^2 -V \cdot V)x + 2(x \cdot v)v - 2s(x \times v)\}) \\
\end{align}
変換 　p \rightarrow qpq^{-1}をA_qで表すと

一般の四元数による変換公式 \\
A_q(p) = qpq-{-1} = (w, \frac{1}{|q|^2}\{(S^2 -V \cdot V)x + 2(x \cdot v)v - 2s(x \times v)\}) \\
ただし、q \neq 0 \\

 ロドリゲスの回転公式と比較任意の点P(位置ベクトルp)を四元数p = (0, p)と同一視したとする。

前述の公式のw = 0, x = pとし、qをq = (\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2}a)) = (s, v), |a| = 1の形の単位四元数とし、A_q(p)の右辺の各項を代入して計算してみる

\begin{align}
& s = \cos \frac{\theta}{2}, v= \sin \frac{\theta}{2}a, |a| = 1より、 \\
&  s^2 - v \cdot v = \cos^2 \frac{\theta}{2} - |v|^2 = \cos^2 \frac{\theta}{2} - \sin^2 \frac{\theta}{2}|a|^2\\
& = \cos^2 \frac{\theta}{2} - \sin^2 \frac{\theta}{2} = \cos \theta \\
& 2(p \cdot v)v = 2 \sin^2 \frac{\theta}{2}(p \cdot a)a = (1 - \cos \theta)(p \cdot a)a \\
& 2s(p \times v) = 2 \cos \frac{\theta}{2}\sin\frac{\theta}{2}(p \times a) = \sin \theta(p \times a) \\
\end{align}

となる。これらすべてを、A_q(p)に代入すると、

A_q(p) = (0, \cos\theta p + (1 - \cos \theta)(p \cdot a)a - \sin \theta(p \times a)) \\
= (0, \cos\theta p + (1 - \cos \theta)(p \cdot a)a + \sin \theta(a \times p)) \\
ゆえにA_q(p)はベクトル\cos\theta p + (1 - \cos \theta)(p \cdot a)a + \sin \theta(a \times p)と同一される。aは単位ベクトルだから、この式はロドリゲスの回転公式と一致する。

以上をまとめると
単位四元数による回転公式

q = (\cos \frac{\theta}{2}, \sin \frac{\theta}{2}a), |a| = 1のとき、A_q(p) = pqp^{-1}はベクトルpの単位ベクトルaまわりの角\thetaの回転を表す。
※ベクトル p = (p_1, p_2, p_3)は純虚四元数(0, p)　= (0, (p_1, p_2, p_3))と同一視すればよく、またqは単位四元数だから、q^{-1} = \bar{q}が成り立って、A_q(p) = qp\bar{q}と書くことができる。

 ここまでの四元数のまとめつまるところ大事なのは、こんなクウォータ二オンqの(s, v)を設定してあげれば、CGソフトなどで回転してあげれるということ。

q = (s, v)\\
s = \cos \frac{\theta}{2}, v= \sin \frac{\theta}{2}a \\
全然直感的じゃない・

 四元数 クウォータ二オン Refernecehttps://youtu.be/J6ja6UYk6X4
https://qiita.com/ma-oshita/items/4921b616b5738d746602
https://qiita.com/SotaAsai/items/a662c5f4675a1b8985f2
https://www.amazon.co.jp/dp/4627096518/ref=cm_sw_em_r_mt_dp_KGDDE3MDS2TGTM2EPNTF
https://youtu.be/HCTQNJu8OhE
https://youtu.be/g7vsR0l7eBM
https://youtu.be/4QToYqFdgdE

 ロドリゲスの公式の行列表示ロドリゲスの回転公式

p^` = p + \sin \theta (a \times p) + (1-\cos \theta)a \times (a \times p)
これは、内積やら外積やらが使われているので他の変換と組み合わせて使おうとすると計算がめんどい。

回転の変換は1次変換であるため、p \rightarrow	p^`を1次変換として、行列として表しておくと、その他の合成との積で表せるでめっちゃ便利。
3次元ユークリッド空間の上の1次変換F_a : \mathbb{R}^3 \rightarrow \mathbb{R}^3をF_a(p) = a \times pで定義すると、

ベクトルpが単位ベクトルaのまわりに\theta回転する1次変換(ロドリゲスの回転公式)p^` = p + \sin \theta (a \times p) + (1-\cos \theta)a \times (a \times p)は

p^` = (I + \sin \theta F_a + (1-\cos \theta)F_a \circ F_a)(p)
F_a \circ F_aは合成関数を表し、Iは恒等変換を表す。

さらに、a = (a_x, a_y, a_z), p = (p_x, p_y, p_z)とし、対応p \rightarrow a \times pの行列をAとすると、

a \times p = (a_y p_z - a_z p_y, a_z p_x - a_x p_z, a_x p_y - a_y p_x) \\
= 
\begin{bmatrix}
   p_x & p_y & p_z \\
\end{bmatrix}
\begin{bmatrix}
   0 & a_z & -a_y \\
   -a_z & 0 & a_x \\
   a_y & -a_x & 0 \\
\end{bmatrix}
となる。

A = 
\begin{bmatrix}
   0 & a_z & -a_y \\
   -a_z & 0 & a_x \\
   a_y & -a_x & 0 \\
\end{bmatrix}
となり、a \times p = pA、a\times(a\times p) = p A^2となる。

変換F_aの行列はIを3次単位行列として、

F_a = I + \sin \theta A + (1 - \cos \theta)A^2
となる。

 四元数の積の行列表現四元数の回転も行列にしておきたい。
直接A_qの行列を考えていくのは難しいので二つの変換の合成として考えていく。

p = w + p_1 i + p_2 j + p_3 k, q = s + xi + yj + zkを四元数として、qは零でないとする。

pにqを左から掛ける変換を L_q : p \rightarrow qp、右から掛ける変換を R_q : p \rightarrow pqとする。

二つともの変換は四元数の計算規則より、線形写像になっている。

ここでL_q(p) = qpを成分表示すると、

\begin{align}
& L_q(p) = qp = (s + xi + yj + zk)(w + p_1 i + p_2 j + p_3 k) \\
& = (sw - xp_1 - yp_2 - zp_3) + (sp_1 + xw +yp_3 - zp_2)i \\
& + (sp_2 - xp_3 + yw + zp_1)j + (sp_3 + xp_2 - yp_1 + zw)k \\

& = 
\begin{bmatrix}
   w & p_1 & p_2 & p_3 \\
\end{bmatrix}
\begin{bmatrix}
   s & x & y & z \\
   -x & s & z & -y \\
   -y & -z & s & x \\
   -z & y & -x & s \\
\end{bmatrix}

\end{align}
同様に、R_q(p) = pqを行列の積の形にすると

\begin{align}
& R_q(p) = pq = 
\begin{bmatrix}
   w & p_1 & p_2 & p_3 \\
\end{bmatrix}
\begin{bmatrix}
   s & x & y & z \\
   -x & s & -z & y \\
   -y & z & s & -x \\
   -z & -y & x & s \\
\end{bmatrix}

\end{align}
変換L_q, R_qの行列も同じ記号で表すと

L_q = 
\begin{bmatrix}
   s & x & y & z \\
   -x & s & z & -y \\
   -y & -z & s & x \\
   -z & y & -x & s \\
\end{bmatrix},
R_q = 
\begin{bmatrix}
   s & x & y & z \\
   -x & s & -z & y \\
   -y & z & s & -x \\
   -z & -y & x & s \\
\end{bmatrix}

さらに r = |q|とすると R_qの逆行列R_q^{-1}は

R_q^{-1} = \frac{1}{r^2}
\begin{bmatrix}
   s & -x & -y & -z \\
   x & s & z & -y \\
   y & -z & s & x \\
   z & y & -x & s \\
\end{bmatrix}

さらに、A_q(p) = qpq^{-1}を注意すると

A_q(p) = (qp)q^{-1} = (pL_q)q^{-1} = (pL_q)R_q-{-1} = p(L_q R_q^{-1})
または、

A_q(p) = q(pq^{-1}) = q(pR_q^{-1}) = (pR_q^{-1})L_q = p(R_q^{-1}L_q)
となり、これはA_qが合成変換であることを示していて、A_qの行列表現は変換と行列を同じ記号で表すことにすると、


 A_q = L_q R_q^{-1} = R_q^{-1}L_q
= \frac{1}{r^2}
\begin{bmatrix}
   s & x & y & z \\
   -x & s & z & -y \\
   -y & -z & s & x \\
   -z & y & -x & s \\
\end{bmatrix}
\begin{bmatrix}
   s & -x & -y & -z \\
   x & s & z & -y \\
   y & -z & s & x \\
   z & y & -x & s \\
\end{bmatrix}\\

=\frac{1}{r^2}
\begin{bmatrix}
   s^2 + X_1 & 0 & 0 & 0 \\
   0 & s^2 + X_2 & 2xy+2sz & 2xz - 2sy \\
   0 & 2xy - 2sz & s^2 + X_3 & 2yz + 2sx \\
   0 & 2xz + 2sy & 2yz - 2sx & s^2 + X_4 \\
\end{bmatrix}
となる。ここではX_1 = x^2 + y^2 + z^2, X_2 = x^2 - y^2 -z^2, X_3 = -x^2 + y^2 -z^2, X_4 = -x^2 -y^2 + z^2としている。

 Reference