マルコフスイッチングモデルを用いたBTCUSDのレジーム判定
0. はじめに
株式会社オークンで今年度からデータサイエンティストをしています芦野です.
業務では自社開発のシステムトレードにおける定量的分析や機械学習モデルの開発に従事しており,元居た畑(スポーツ科学)とはデータの性質が大きく異なる日々に楽しさを感じています.
本稿では,最近学習を進めている計量時系列分析について,かの有名な沖本本1で特に興味深かった「8. 状態変化を伴うモデル」で紹介されていたマルコフ転換モデル(Markov switching model)をBTC/USDを対象としてpythonで実装してみることを目的としています.
1. 経済・ファイナンスにおける「レジーム」
時間の経過に従って測定されるデータの中でも,経済・ファイナンスのデータは社会経済的な変化に伴ってその挙動や状態が根本的に変わるケースがあると考えられている.この,時系列データにおける挙動や状態は「レジーム」と呼ばれ,状態変化を記述・表現できるモデルをレジームスイッチングモデルと呼ばれる2.
レジームスイッチングモデルは状態が観測可能な変数によって決まるモデルと,状態が観測不可能な変数によって決まるモデルの2つに大別される.経済・ファイナンスにおいては,投資家の心理や各国の景気など不可視な変数によって大きく影響を受けると考えられる.
2. マルコフスイッチングモデルについて
2.1 隠れ状態とレジームの考え方
前節で述べたように,経済・ファイナンスの時系列データは,「平穏」「強気」「クラッシュ」のような**質的に異なる状態(レジーム)**を行き来していると考えられることが多い.
本稿では,日次BTCリターン系列を
直感的には,
・
・
・
のように,「その日がどのレジームに属しているか」を表すラベルを
2.2 マルコフ連鎖による状態遷移
レジームの時間的な推移は,通常 マルコフ連鎖(Markov chain) に従うと仮定する.
レジームの数を
と書くことができる.ここで
を遷移確率行列(transition probability matrix)と呼ぶ.各行は確率のベクトルなので,
・各要素は
・各行の和は
を満たす.
この遷移行列からは,
・各レジームの平均滞在期間
・長期的な出現比率を表す定常分布
などの量を計算することができる.本稿の後半では,実データから推定された
2.3 観測方程式:MS-AR モデルの定式化
マルコフスイッチングモデルでは,隠れ状態
一般的なマルコフスイッチング自己回帰モデル(Markov Switching AutoRegressive model; MS-AR(
のように表される.
ここで,
・
・
・
であり,平均・自己回帰係数・分散がレジームごとに異なることを許容している.
2.4 本稿で用いるモデル仕様
本稿では,まず単一レジームのAR(1)モデルを推定し,BTC/USDT日次リターンに弱い自己相関が存在する一方で,単一ガウス分布では裾の重さや異分散を説明しきれないことを確認する.
そのうえで,「AR(1)構造は維持しつつ,平均と分散だけをレジームごとに変化させる」マルコフスイッチング(MS)AR(1)モデルを採用する.
具体的には,レジーム数
という形の MSAR(1) モデルを用いる.ここで,
・
・
・
とすることで,単一レジームAR(1)モデルとの比較がしやすく,「レジーム間の違い」を平均とボラティリティの違いとして素直に解釈できるという利点がある.
以降では,この MSAR(1)モデルを用いて,まず
3. 実験対象
対象は,ccxtで取得可能であった 2017-08-17〜2025-12-12 のBTC/USDT日足(Binance) とした.分析では終値から日次リターン系列retを構成し,単一レジームモデル(AR(1))とマルコフスイッチングモデル(MSAR(1))を比較する.

Fig 1 2017年08月17日から2025年12月12日までのBTC/USDTの終値推移
データ取得コード(ccxt)
import ccxt
import pandas as pd
import time
from datetime import datetime, timezone
exchange = ccxt.binance()
def fetch_ohlcv_all(
symbol: str,
timeframe: str = "15m",
since: int | None = None, # ms
limit: int = 1000,
until: int | None = None, # ms, ここまで欲しい場合
):
"""
Binance など 1回 N 本制限のある取引所から
OHLCV をページングして全部取ってくる
"""
if since is None:
# 2017-01-01 UTC から
since_dt = datetime(2017, 1, 1, tzinfo=timezone.utc)
since = int(since_dt.timestamp() * 1000)
if until is None:
until = exchange.milliseconds()
timeframe_ms = exchange.parse_timeframe(timeframe) * 1000
all_ohlcv: list[list] = []
while since < until:
ohlcv = exchange.fetch_ohlcv(
symbol=symbol,
timeframe=timeframe,
since=since,
limit=limit,
)
if not ohlcv:
break
all_ohlcv.extend(ohlcv)
last_ts = ohlcv[-1][0]
# 同じ足を2回取らないように+1本分進める
since = last_ts + timeframe_ms
# 返ってきた本数が limit 未満なら終端まで来たと判断
if len(ohlcv) < limit:
break
# レートリミット対策
time.sleep(exchange.rateLimit / 1000)
return all_ohlcv
symbol = "BTC/USDT"
timeframe = "1d"
all_ohlcv = fetch_ohlcv_all(symbol, timeframe=timeframe, limit=1000)
cols = ["timestamp", "open", "high", "low", "close", "volume"]
df = pd.DataFrame(all_ohlcv, columns=cols).drop_duplicates(subset="timestamp")
df["timestamp"] = pd.to_datetime(df["timestamp"], unit="ms", utc=True)
df = df.set_index("timestamp").sort_index()
print(df.head(), df.tail(), len(df))
4. 単一レジームモデルからマルコフスイッチングモデルへの拡張
この節では,(i)単一レジームのAR(1)と,(ii)平均・分散がレジームで切り替わるMSAR(1)(2レジーム/3レジーム)を順に推定し,適合度と解釈可能性を比較する.
4.0 モデル比較(結論)
情報量基準の観点では,AR(1) → 2レジームMSAR(1) → 3レジームMSAR(1)の順に改善した.特に2レジーム化で大幅に適合度が改善し,3レジーム化でさらに上積みが得られた.
| Model | LogLik | AIC | BIC | 要点 |
|---|---|---|---|---|
| AR(1) | 5769.3 | -11532.7 | -11514.6 | 単一ガウスは厚尾・ヘテロを説明しにくい |
| 2-regime MSAR(1) | 6224.1 | -12434.1 | -12392.0 | 低ボラ/高ボラの切替が表現可能 |
| 3-regime MSAR(1) | 6315.7 | -12605.4 | -12527.2 | 平穏/強気/クラッシュの分解がより明確 |
4.1 AR(1)モデル
まずは,基本的な自己回帰モデルであるAR(1)モデルによる単一レジームを仮定としたモデリングを実施してみる.
from statsmodels.tsa.arima.model import ARIMA
ar1_model = ARIMA(ret, order=(1, 0, 0))
ar1_res = ar1_model.fit()
print(ar1_res.summary())
結果の要点:
・定数項は0.001(p≧.11)で,平均リターンはわずかに正だが 統計的に有意ではない.
・AR(1)係数は-0.051(p<.01)で,自己相関は強くないが 弱い平均回帰が示唆される.
.一方で残差診断(JB,分散一定性)から,正規性・分散一定性が強く棄却され,単一ガウスレジームの前提は弱い.
したがって,BTC日次リターンは「平均・分散が時期によって変化する」可能性が高く,次に レジーム切替を導入したMSAR(1)を検討する.
AR(1) summary全文
SARIMAX Results
==============================================================================
Dep. Variable: close No. Observations: 3038
Model: ARIMA(1, 0, 0) Log Likelihood 5769.338
Date: Thu, 11 Dec 2025 AIC -11532.675
Time: 09:22:11 BIC -11514.619
Sample: 08-18-2017 HQIC -11526.185
- 12-11-2025
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0010 0.001 1.561 0.119 -0.000 0.002
ar.L1 -0.0509 0.012 -4.329 0.000 -0.074 -0.028
sigma2 0.0013 1.17e-05 112.395 0.000 0.001 0.001
===================================================================================
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 31400.62
Prob(Q): 0.90 Prob(JB): 0.00
Heteroskedasticity (H): 0.28 Skew: -1.00
Prob(H) (two-sided): 0.00 Kurtosis: 18.62
===================================================================================
4.2 2レジームMSAR(1)モデル
次に,AR(1)構造は維持したまま,平均と分散がレジームごとに異なる2レジームMSAR(1)を推定する(AR係数は共通,μ・σ²のみスイッチ).
from statsmodels.tsa.regime_switching.markov_autoregression import MarkovAutoregression
# 2レジーム MSAR(1)(φは共通、μ・σ2はレジーム依存)
msar2_model = MarkovAutoregression(
ret,
k_regimes=2,
order=1, # AR(1)
trend="c", # 定数項あり
switching_ar=False, # φ は全レジームで共通
switching_trend=True, # μ_k はレジームごと
switching_variance=True, # σ_k^2 もレジームごと
)
msar2_res = msar2_model.fit()
適合度(AR(1)との比較)
・LogLikは約 +400,AIC/BICは約 -900 改善した.
→単一レジームAR(1)より2レジームMSAR(1)の方が適合度が高い.
またAR係数は -0.074 と大きくは変わらず,「弱い平均回帰はあるが自己相関は強くない」という見立て自体は維持される.
レジームの解釈(平均・分散)
推定された平均と標準偏差は以下の通り.
- Regime 0: 低ボラかつわずかにプラスの「穏やかなレジーム」
- Regime 1: ボラティリティが高くリスクの大きい「乱高下レジーム」
| Regime | mean(日次) |
|
解釈 |
|---|---|---|---|
| 0 | 0.0012 | 低ボラかつわずかにプラスのレジーム | |
| 1 | 0.0007 | 高ボラ・平均は 0 に近いレジーム |
遷移確率と滞在期間
遷移行列の推定値は概ね
となり,各レジームの平均滞在期間は
となる.つまり,穏やかなレジームは平均して6.1日,乱高下するレジームは平均して3.4日継続すると推定される.
また,定常分布を計算すると,
となる.これは,長期的には全体の6〜7割の時間を穏やかなレジームで過ごし,残りの3〜4割の時間を乱高下レジームで過ごしている,と解釈できる.実際に推定されたレジームを価格系列上に重ねてプロットすると,乱高下するレジーム(Regime 1)の頻度は穏やかなレジームに比べて低く,継続も短いことが見てとれる.
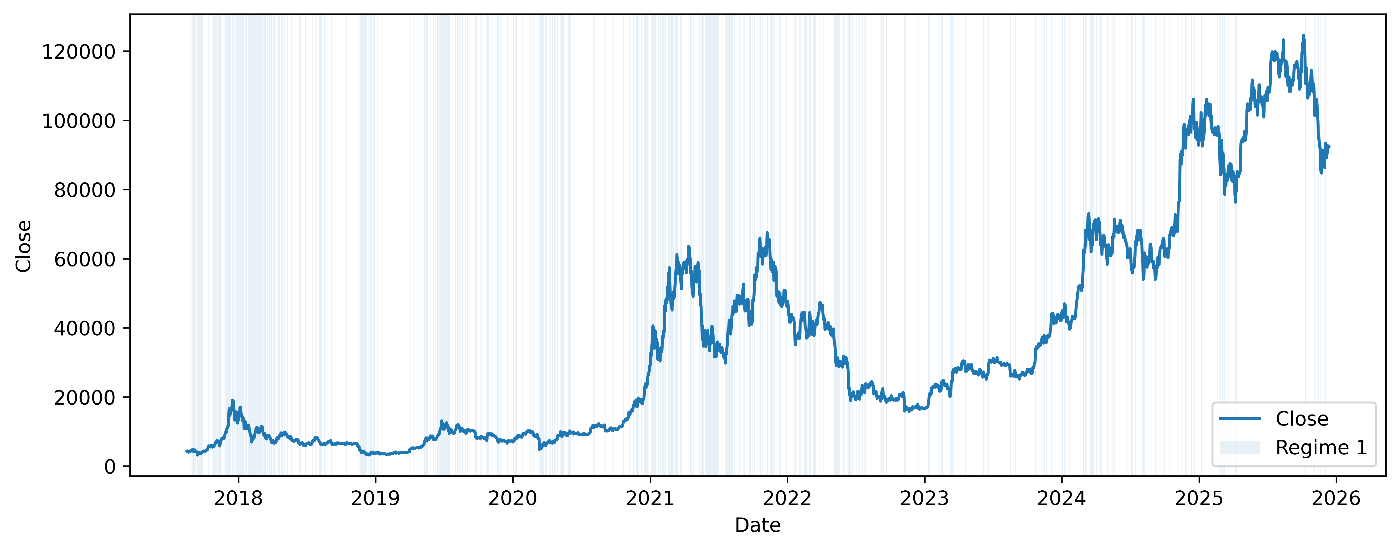
Fig 2 2レジームMSAR(1)モデルによる推定レジームの可視化
2レジームの限界
高ボラレジーム(Regime 1)の平均は0と有意に区別できず,「強気の上昇」と「急落・クラッシュ」が同一の高ボラ状態に混在している可能性がある.
そこで次節では,3レジーム化により分解が改善するかを検討する.
2レジームMSAR(1)summary全文
Markov Switching Model Results
================================================================================
Dep. Variable: close No. Observations: 3038
Model: MarkovAutoregression Log Likelihood 6224.055
Date: Fri, 12 Dec 2025 AIC -12434.111
Time: 14:43:31 BIC -12391.978
Sample: 08-18-2017 HQIC -12418.965
- 12-12-2025
Covariance Type: approx
Regime 0 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0012 0.000 2.660 0.008 0.000 0.002
sigma2 0.0003 2.57e-05 11.323 0.000 0.000 0.000
Regime 1 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0007 0.002 0.433 0.665 -0.003 0.004
sigma2 0.0031 0.000 15.147 0.000 0.003 0.004
Non-switching parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.0741 0.017 -4.391 0.000 -0.107 -0.041
Regime transition parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
p[0->0] 0.8356 0.027 30.793 0.000 0.782 0.889
p[1->0] 0.2921 0.047 6.249 0.000 0.200 0.384
==============================================================================
4.3 3レジームMSAR(1)モデル
2レジームの「高ボラに強気とクラッシュが混ざる」問題を緩和するため,3レジームMSAR(1)を推定する.
適合度(2レジームとの比較)
2レジームに比べて LogLikは約 +90,AIC/BICは約 -150 改善した.
→ 情報量基準上,3レジームMSAR(1)が最も適切となった.
3レジームMSAR(1)summary全文
Markov Switching Model Results
================================================================================
Dep. Variable: close No. Observations: 3038
Model: MarkovAutoregression Log Likelihood 6315.718
Date: Fri, 12 Dec 2025 AIC -12605.435
Time: 15:36:21 BIC -12527.189
Sample: 08-18-2017 HQIC -12577.308
- 12-12-2025
Covariance Type: approx
Regime 0 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0005 0.000 1.083 0.279 -0.000 0.001
sigma2 0.0001 1.81e-05 7.148 0.000 9.41e-05 0.000
Regime 1 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0026 0.001 2.387 0.017 0.000 0.005
sigma2 0.0013 0.000 11.814 0.000 0.001 0.002
Regime 2 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0018 0.003 -0.587 0.557 -0.008 0.004
sigma2 0.0042 0.000 10.597 0.000 0.003 0.005
Non-switching parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.0745 0.017 -4.445 0.000 -0.107 -0.042
Regime transition parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
p[0->0] 0.6477 0.046 14.228 0.000 0.558 0.737
p[1->0] 0.3184 0.049 6.441 0.000 0.222 0.415
p[2->0] 2.071e-05 0.053 0.000 1.000 -0.104 0.104
p[0->1] 0.3522 0.045 7.851 0.000 0.264 0.440
p[1->1] 0.6661 0.049 13.461 0.000 0.569 0.763
p[2->1] 0.0429 0.046 0.929 0.353 -0.048 0.134
==============================================================================
レジームの解釈(平穏/強気/クラッシュ)
| Regime | mean(日次) |
|
解釈 |
|---|---|---|---|
| 0 | 0.0005 | 低ボラ・平均ほぼ0の平穏レジーム | |
| 1 | 0.0026 | 中ボラ・有意にプラスの強気レジーム | |
| 2 | -0.0018 | 高ボラ・平均はマイナス寄りのクラッシュ/乱高下レジーム |
Regime 1 は平均が0より有意に大きく(p=0.017),強気局面として自然に解釈できる.一方,Regime 2 は平均は有意でないが高ボラであり,クラッシュ/乱高下に対応する状態とみなせる.
遷移確率と滞在期間
定常分布は,
平穏と強気は数日単位で入れ替わる一方,クラッシュレジームは一度入ると比較的長く滞在しやすいという推定結果となった.
しかしながら,2023年以降にクラッシュレジームがほとんど出現しない点は「相場が実際に安定していた」可能性と「モデルがクラッシュを検出できていない」可能性の両方があるため,別期間・別仕様での検証余地が残る.
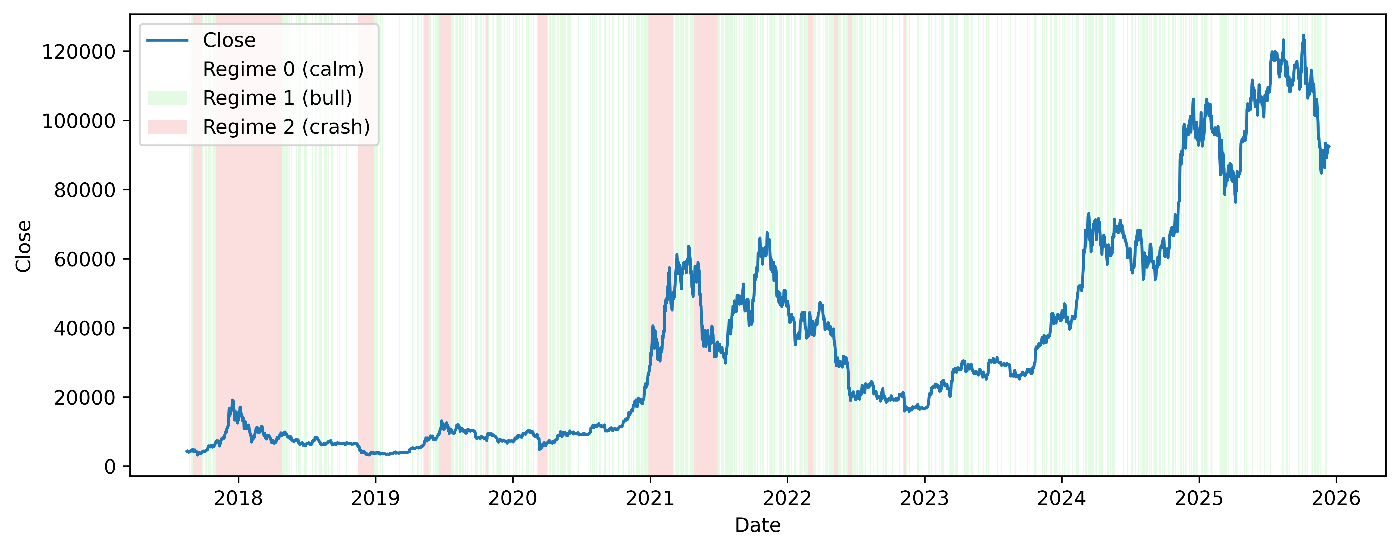
Fig 3 3レジームMSAR(1)モデルによる推定レジームの可視化
5. 結論と今後の展望
本稿では,2017-08-17〜2025-12-12 のBTC/USDT日次データに対し,AR(1),2レジームMSAR(1),3レジームMSAR(1)を比較した.情報量基準(AIC/BIC)では,AR(1)<2レジーム<3レジームの順に適合度が改善し,MSAR(1)がBTC日次リターンの状態依存性(特にボラティリティ)を捉える上で有効であることが示唆された.
得られた示唆
・単一レジームのガウスAR(1)は,弱い平均回帰は拾う一方,厚尾・ヘテロを説明しきれない
・2レジームMSAR(1)は,低ボラ/高ボラの切替を表現でき,ボラティリティ・クラスタリングと整合的である
・3レジームMSAR(1)では,平穏/強気/クラッシュの3状態が得られ,2レジームで混在しがちな局面分解が改善した
限界
・観測分布をガウスに固定しており,レジーム内の厚尾や歪度は明示的に表現していない
・ボラティリティは分散スイッチのみで表現しており,GARCH型の持続性は組み込んでいない
・遷移確率を時間一定としたため,市場環境による遷移の変化や,特定期間でのレジーム検出の妥当性は追加検証が必要である
今後の展望
・t分布やMS-GARCH等を導入し,尾部リスクとボラティリティ持続性を同時に扱う
・出来高や金利等の共変量を含むモデルに拡張し,レジーム遷移の要因を検討する
・推定レジームに応じたリスク制御(ポジションサイズ調整等)を設計し,バックテストで有用性を評価する
6. 文献など
[1]沖本竜義(2010)経済・ファイナンスデータの計量時系列分析 (統計ライブラリー).朝倉書店.
[2]沖本竜義(2014)マルコフスイッチングモデルのマクロ経済・ファイナンスへの応用.日本統計学会誌,44(1),137-157.
7. 最後に
ご覧いただきありがとうございました!
弊社では,ヘッジファンド向けのトレードシステム開発・運用をしております.
データ基盤からモデル開発,バックテスト,実運用まで一気通貫で携わることができる環境です.
本稿のテーマに関心のある方がいれば,ぜひ株式会社オークンについてものぞいてみてください!
Discussion