📈
統計学のメモ #3 大数の法則と中心極限定理
統計学に入門したので備忘録をまとめていきます。
この記事では、大数の法則と中心極限定理について書きます。
大数の法則 / law of large numbers
同一の試行を数多く繰り返すことにより、標本平均が理論上の値(=母平均)に近づくという法則のこと。
実験してみる
コインを10回投げて50%の確率で表が出る二項分布から、500のサンプルを抽出し、その平均値の推移をグラフにしてみる。
> result <- rbinom(500, 10, 0.5)
> prob <- c(cumsum(result) / 1:500)
> plot(prob, xlab="n", ylab="mean", type="l")
> abline(h = 5.0, col="red")
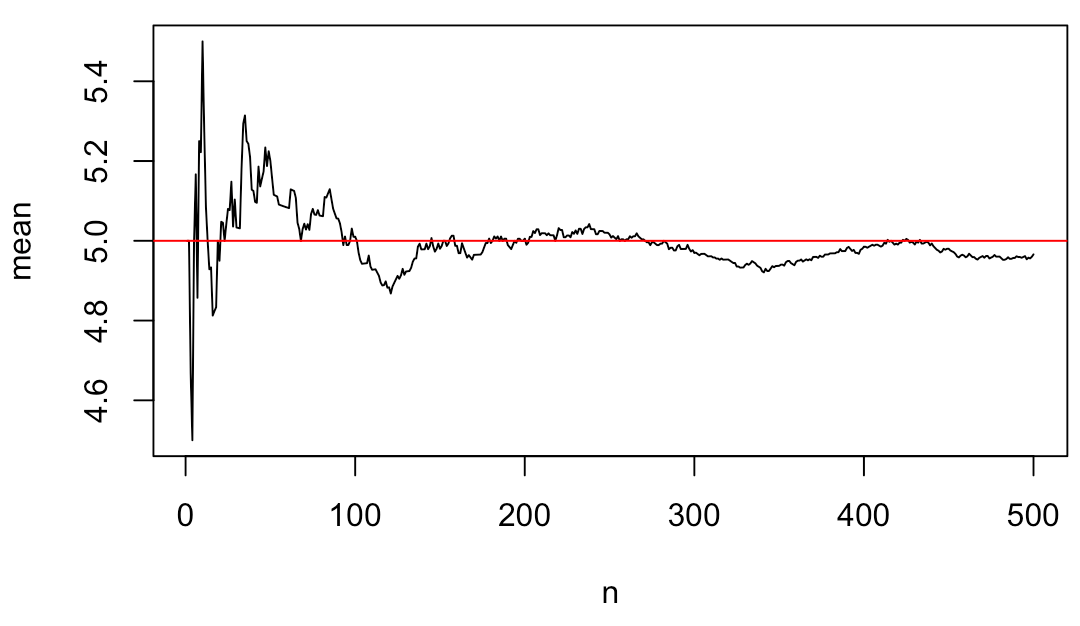
コインを投げる回数nが大きくなるほど理論上の平均値5に近づいていることがわかる。
中心極限定理 / central limit theorem (CLT)
母集団がどのような分布に従っていても、標本サイズが十分に大きければ、標本平均の分布は正規分布に従う。この一般的原理を中心極限定理という。
実験してみる
Poisson(3)に従う乱数を10万個生成して母集団とする。
> population <- rpois(100000, 3)
> hist(population)
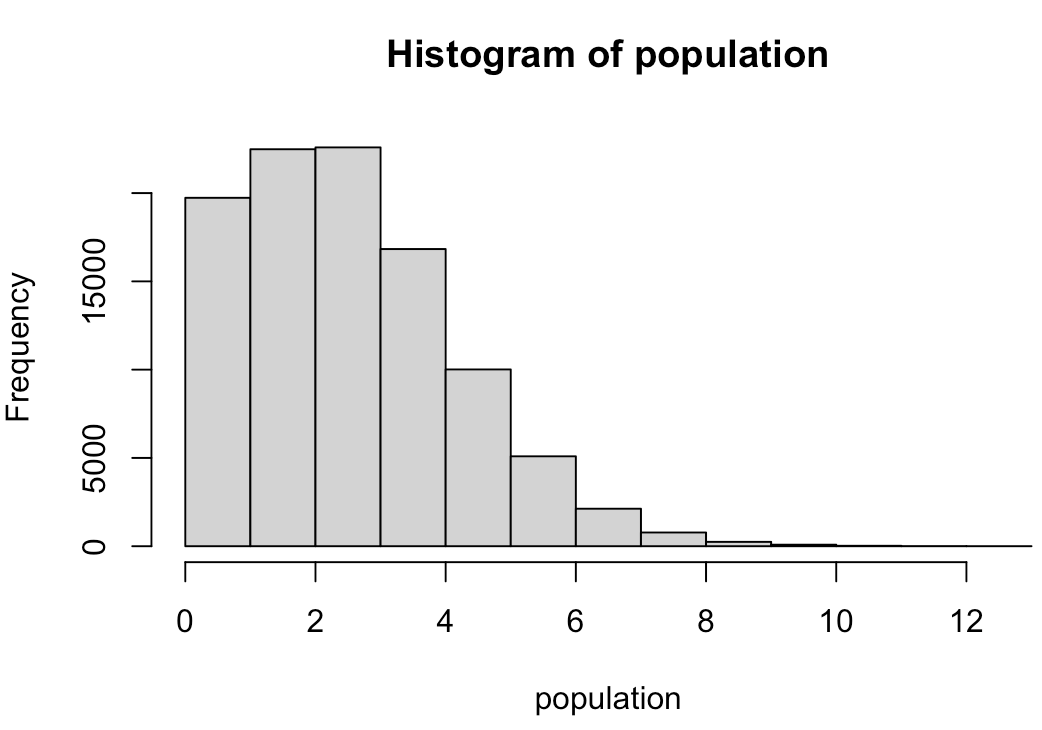
母集団から任意の標本サイズを無作為抽出し、その平均値を求める操作を1000回繰り返してベクトルを作る関数を定義。
> sampling_dist <- function(population, sample_size) {
+ means <- c()
+ for (i in 1:1000) {
+ samples <- sample(population, sample_size)
+ means <- c(means, mean(samples))
+ }
+ return(means)
+ }
標本サイズ3で試してみる。
> test3 <- sampling_dist(population, 3)
> hist(test3)

標本サイズが少なすぎて綺麗な正規分布にならなかった。
標本サイズ100で試してみる。
> test100 <- sampling_dist(population, 100)
> hist(test100)

正規分布にかなり近づいた。
母集団の平均・標準偏差と比べてみてもほぼ一致している。
> mean(test100)
[1] 2.99735
> sd(test100)
[1] 0.1777202
> mean(population)
[1] 2.99905
> sd(population)/sqrt(100)
[1] 0.1725001


Discussion