統計学のメモ #2 確率分布
統計学に入門したので備忘録をまとめていきます。
この記事では、確率の基本用語とさまざまな確率分布について書きます。
標本空間、事象
-
試行 / trial
- ある特定の条件のもとで繰り返し行うことができ、その結果が偶然に決まる実験
- e.g. サイコロを一回投げる行為
-
標本点 / sample point
\omega - 試行において起こり得る個々の結果
- e.g. サイコロを一回投げて出る目の標本点
1, 2, 3 ... 6の目が出る
-
標本空間 / sample space
\omega \in \Omega - すべての標本点からなる集合
- e.g. サイコロを一回投げて出る目の標本空間
{1, 2, 3, 4, 5, 6}
-
事象 / event
- 試行において起こり得る結果。標本空間の部分集合。
- e.g. サイコロを一回投げて、奇数の目が出る事象
{1, 3, 5}
-
根元事象 / elementary event
- それ以上分けることができない、標本点が一つの事象。
- e.g. サイコロを一回投げて出る目の根元事象
{1}, {2}, {3}, {4}, {5}, {6}
| その他の事象 | 記号 | 意味 |
|---|---|---|
| 全事象 | 標本空間全体 | |
| 空事象 | 何も起こらない | |
| 余事象 | Aは起こらない | |
| 積事象 | AとBが同時に起こる | |
| 和事象 | 少なくともAかBの一方が起こる | |
| 排反事象 | AとBは同時に起こらない |
確率変数、期待値、分散
-
確率変数 / random variable
- ある現象を観測する際に、どのような値をとるか決まっていないが、その確率を割り当てられる変数
- 大文字で
X, Y, Z - 確率変数がとる値は小文字で
x_{1}, ...,x_{k} -
離散確率変数 / discrete random variable
- 飛び飛びの値に確率が割り当てられる変数
- e.g. サイコロを一回投げて出る目の数
-
連続確率変数 / continuous random variable
- 連続する値に確率が割り当てられる変数
- e.g. 身長、時間など
-
期待値 / expectation
E(X) - 確率変数がとり得る値の平均値
- 母平均
\mu
-
確率変数の分散 / variance
V(X) - 確率変数Xのとり得る値が期待値の周りにどの程度ばらついているかを表す
- 偏差の二乗と対応する確率との加重和
- 確率変数の分散は「期待値」のように特別な呼び名は無く、そのまま「分散」という
確率分布とは
すべての排反事象とその確率を対応させたものを 確率分布(probability distribution) という。
e.g. サイコロを一回投げて出る目の確率分布
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
- それぞれの確率は0〜1の間にある
- 確率の和は1になる
確率分布を表す関数
確率質量関数 / probability mass function, PMF
離散確率変数
単に確率関数(probability function)ともいう。
確率密度関数 / probability density function, PDF
連続確率変数
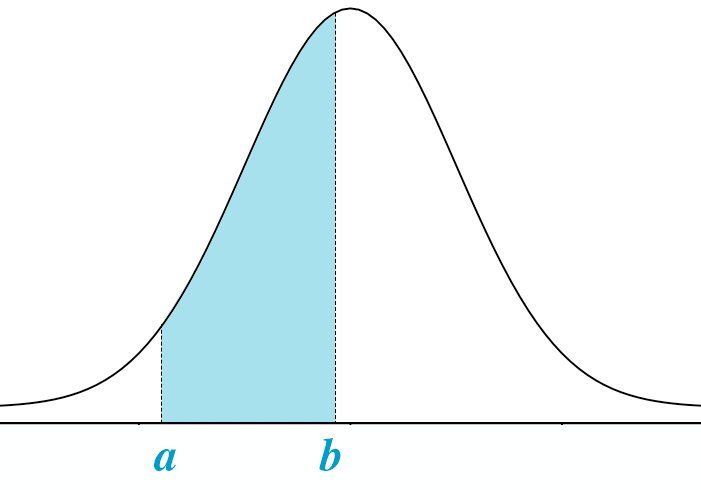
この面積が確率となる。
累積分布関数 / cumulative distribution function
確率変数
離散型確率分布
| 式 | |
|---|---|
| 確率質量関数 | 確率変数 以下性質を持つ。 |
| 期待値 | |
| 分散 | |
| 標準偏差 | |
| 累積分布関数 | 確率変数 |
二項分布 / Binominal distribution
コインを投げて表が出るか裏が出るかのように、とり得る結果が2つしかない試行のことを ベルヌーイ試行 という。ベルヌーイ試行を繰り返し、成功する回数
| 記号 | 意味 |
|---|---|
| 試行回数 | |
| 成功確率 |
二項分布の式
成功確率
二項分布のRの関数
Binomial(30, 0.2)の場合
# x = 10 の確率
> dbinom(10, size=30, prob=0.2)
[1] 0.03547089
# x <= 6 の確率
> pbinom(6, size=30, prob=0.2)
[1] 0.6069699
# 25パーセンタイルとなる値
> qbinom(0.25, size=30, prob=0.2)
[1] 3
グラフ
> x <- 0:20
> plot(x, dbinom(x, size=30, prob=0.2), type="h", lwd=5)

Binomial(30, 0.2)に従う10個の乱数を生成
> rbinom(10, size=30, prob=0.2)
[1] 7 6 4 7 6 7 5 4 10 6
ポアソン分布 / Poisson distribution
e.g. 15分に平均3回電話がかかってくるコールセンターで、1時間に20回電話がかかってくる確率
| 記号 | 意味 |
|---|---|
| 期待値 |
ポアソン分布の式
単位時間あたりにある事象が平均して
ポアソン分布のRの関数
Poisson(3)の場合
# x = 0 の確率
> dpois(0, lambda=3)
[1] 0.04978707
# x <= 2 の確率
> ppois(2, lambda=3)
[1] 0.4231901
# 25パーセンタイルとなる値
> qpois(0.25, lambda=3)
[1] 1
グラフ
> x <- 0:15
> plot(x, dpois(x, lambda=3), type="h", lwd=5)

Poisson(3)に従う10個の乱数を生成
> rpois(10, lambda=3)
[1] 8 2 2 3 3 2 2 5 3 2
連続型確率分布
| 式 | |
|---|---|
| 確率密度関数 | 連続確率変数 以下性質を持つ。 |
| 期待値 | |
| 分散 | |
| 標準偏差 | |
| 累積分布関数 | 確率変数 |
連続一様分布 / continuous uniform distribution
確率変数
e.g. 1〜6の範囲で10万個の乱数を作り、その中からある値を選ぶ確率
| 記号 | 意味 |
|---|---|
| 確率変数 |
|
| 確率変数 |
連続一様分布の式
確率変数
連続一様分布のRの関数
Uniform(1, 6)の場合
# x = 1 の確率
> dunif(1, min=1, max=6)
[1] 0.2
# x <= 3 の確率
> punif(3, min=1, max=6)
[1] 0.4
# 25パーセンタイルとなる値
> qunif(0.25, min=1, max=6)
[1] 2.25
グラフ
> curve(dunif(x, min=1, max=6), from = 0, to = 10)

Uniform(1, 6)に従う10個の乱数を生成
> runif(10, min=1, max=6)
[1] 0.93176768 1.68420630 0.04249733 0.61393926 0.16575856 0.39357959
[7] 0.13956209 1.20598304 0.76407702 0.12515356
指数分布 / exponential distribution
「ある期間に平均して
e.g. 電球が切れる間隔、次に機会が故障するまでの期間
| 記号 | 意味 |
|---|---|
| レート。単位時間あたりの平均発生回数 |
指数分布の式
ある期間に平均して
指数分布のRの関数
Exponential(2)の場合
# x = 1 の確率
> dexp(1, rate=2)
[1] 0.2706706
# x <= 2 の確率
> pexp(2, rate=2)
[1] 0.9816844
# 25パーセンタイル
> qexp(0.25, rate=2)
[1] 0.143841
グラフ
> curve(dexp(x, rate=2), from = 0, to = 5)

Exponential(2)に従う10個の乱数を生成
> rexp(10, rate=2)
[1] 0.93176768 1.68420630 0.04249733 0.61393926 0.16575856 0.39357959
[7] 0.13956209 1.20598304 0.76407702 0.12515356
正規分布 / normal distribution
ガウス分布とも呼ばれる代表的な連続型確率分布。身近にあるさまざまな社会現象や自然現象を表すモデルとして用いられている。
分布が数学的に扱いやすい性質を持っているため、統計分析によく用いられる重要な確率分布。
- 平均値と中央値が同じ
- 平均値に近い値の頻度が高く、平均値から離れるほど頻度が低くなる
- 平均値
x=\mu
| 記号 | 意味 |
|---|---|
| 平均 | |
| 分散 |
正規分布を標準化した
正規分布の式
正規分布に従う確率変数
正規分布のRの関数
Normal(40, 10)の場合
# x = 30 の確率
> dnorm(30, mean=40, sd=10)
[1] 0.02419707
# x <= 30 の確率
> pnorm(20, mean=40, sd=10)
[1] 0.02275013
# 25パーセンタイルとなる値
> qnorm(0.25, mean=40, sd=10)
[1] 33.2551
グラフ
> curve(dnorm(x, mean=40, sd=10),0,80)

Normal(40, 10)に従う10個の乱数を生成
> rnorm(10, mean=40, sd=10)
[1] 40.89110 47.80679 18.50429 42.50225 14.39112 45.97649 40.40319 55.36950
[9] 31.43789 32.31698
Discussion