受験者毎に適切な問題を出しわける試験の仕組みをAutoEncoderとみなして実装する
世の中には受験者毎に最適化された問題が出題される試験があります。
例えば日本人向けの英語テスト CASEC では、「日本初のアダプティブ(適応型)なテスト!」を謳っており、従来のペーパーテストと比べて短時間で正確な測定が可能となっている[1]そうです。
CASEC のこちらのページでは、その仕組みを視力検査に準えてわかりやすく説明してくれています。以下の図のように、それまでの解答履歴を元に、出題する難易度を調整する、というのが基本方針のようです。

CATの仕組み 引用元: CASEC
さて、こういった試験はコンピューター適応型試験(Computer Adaptive Test, 以下 CAT)と呼ばれます。CATは、受験者にとっては(本当に正しい結果なのか不安だったりするものの)無駄な設問が減って試験時間が短くなるメリットがあります。また、CATのように人によって設問を変えたり設問数を少なくする手法は、試験以外にも学習時間の短縮、アンケートや性格検査、問診など色々なところで応用ができそうです。
個人的な話として次の4月に息子が小学生になることもあって最近教育に強く興味があるのですが、CATが面白そうだったので、その仕組みについて調べて独自に実装してみようと思います。
CAT の仕組み
CAT を構築・実施するまでの流れをざっと整理すると以下のようになります。
- 設問準備
何はともあれ出題候補となる設問が必要です。受験者毎に設問が変わるため、従来の試験よりも大量の設問が必要となります。 - プレテスト
用意した設問が適切かどうか、また、その設問の難易度(困難度と呼ぶことが多いです)はどの程度かを把握する必要があります。そのため、事前に大量の被験者を用意して用意した問題を解いてもらいます。- プレテストの結果、困難度等の性質がわかった設問の集合を項目プールと呼びます
- 困難度等の性質を推定する方法として項目反応理論が使われることが多いです
- 設問の取捨選択
プレテストの結果、性質の悪い(例えば、得点の高い人ほど正解率の低い引っ掛け問題など)を除去し、CATの出題候補となる設問を整備します- ここで出題候補となった設問の集合を項目バンクと呼びます
- CAT の実施
- 最初の問題を選定
- 解答毎に能力値を推定し、次の設問を選定
-
- を繰り返し、あらかじめ設定していた終了条件を満たしたら終了する
また、上記の流れに加え、設問の追加・削除等のメンテナンスが発生します。
項目反応理論の基礎
さて、CATの肝は受験者の能力に基づいて、適切な設問を選択することでした。この選択には、2.プレテストで項目反応理論を用いて推定した困難度等の性質が使われます。そこで、ここで項目反応理論の基本的な事項を紹介します。
基本的な考え方
項目反応理論では、「受験者の能力値
ここで
-
\theta_a = \beta_i \frac{1}{(1 + \exp(0))} = \frac{1}{2} -
\alpha_i = 0 0 \frac{1}{(1 + \exp(0))} = \frac{1}{2} \alpha_i \theta_a < \beta_i \theta_a > \beta_i
という性質があります。このことから、
なお、
-
受験者の能力値
\theta_{a} \beta_{i} \alpha_{i} -
問題の困難度
\beta_{i} \alpha_{i} \theta_{a}
という襷掛け構造になっています[2]。
項目反応理論とCAT
項目反応理論を利用してCATを実現するには、項目情報量
ここで、
詳細については以下項目反応理論(2PLモデル)の基礎事項と項目情報量をご覧いただくとして、上の式をじっと眺めると、
-
\alpha_i - 識別力が高い問題。言い換えると良問
-
P_i(\theta_a)
たしかに、直感的にもよさそうです。なお、項目情報量を全ての問題について足し合わせた量を試験情報量と呼び、こちらは個別の問題ではなく、その試験そのものの良さを表す[5]指標となっています。
項目反応理論(2PLモデル)の基礎事項と項目情報量
能力値、困難度、識別力の関係
能力値
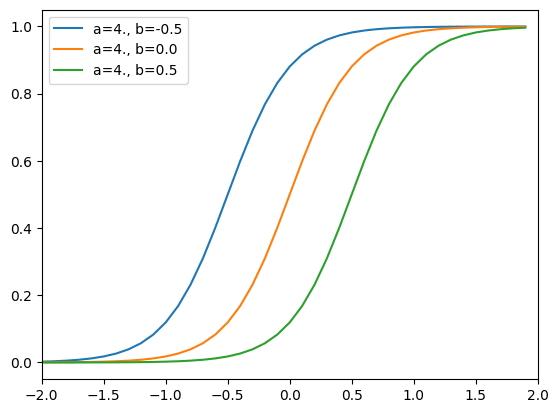
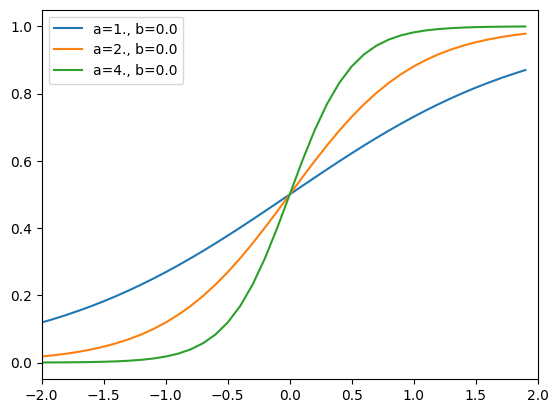
図から分かる通り、
能力値の推定とテストの良さ(精度)
項目反応理論では、「受験者の能力値
-
\theta_{a}
ということができます。
となります。ここで、
IRTでは、
横軸を
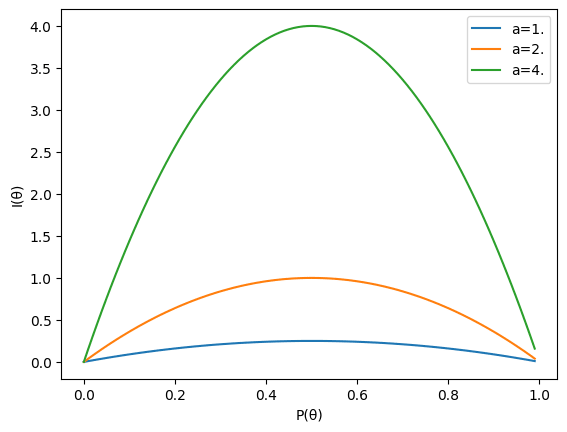
ここから、
-
I_i(\theta_a) \alpha_{i} -
I_i(\theta_a) P(\theta_a) 1/2 - つまり、 能力値と困難度が等しい
\theta_a = \beta
- つまり、 能力値と困難度が等しい
ということがわかります。また、受験者が問題を解くたびに
データセット
今回は Kaggle にある Dichotomous Data for Item Response Theory を使って実験を行いました。60問から構成される4択形式の試験の実際の解答データで、以下のような形式になっています(正答の場合に
| Student ID | 1.If the radius of earth ... | 2.A cable that can support a ... | 3.Boiling water is changing into steam. ... | ... |
|---|---|---|---|---|
| ... | ... | ... | ... | ... |
| 3402 | 0 | 0 | 0 | ... |
| 2179 | 1 | 1 | 1 | ... |
| 1061 | 1 | 0 | 1 | ... |
| 2781 | 1 | 1 | 1 | ... |
| 3688 | 1 | 0 | 1 | ... |
以下の実験では、この受験者の1割を検証用としてとっておき、残りの9割を訓練用としました。
CATの実装
CATでは項目情報量を計算するため困難度と識別力、(それまでの解答結果に基づく)能力値を推定する必要があります。
もっとも単純な方法は、項目反応理論はロジスティック回帰の襷掛けのようなものなので、
- 2パラメータモデルでは、収束しないことが多い
- 受験者数を増やせば増やすほど、推定すべきパラメーターが増えてしまい、結果、項目パラメーターの推定値が真の値に一致しない
という問題があるそうです[8]。この問題を克服した推定手法はいくつかある[9]ようですが、ここでは実装と拡張の容易性から、
- 項目パラメーター(
\alpha_{i} \beta_{i} - 能力パラメーター (
\theta_a - 確率的勾配降下法を用いて最尤推定を行う
という方針で推定することにしました。この方法であれば、受験者が増えたとしても、各
困難度と識別力の推定
前述の方針に基づいて Keras で実装すると、以下のようになります。受験者のIDを受け取って各設問の正答確率を返しています。
class IRT2PLLayer(tf.keras.layers.Layer):
def __init__(self, n_questions, **kwargs):
"""2パラメーターモデルに基づいて、正答確率を出力するレイヤー
params:
n_questions (int): 設問数
"""
super().__init__(**kwargs)
self.n_questions = n_questions
self.a = self.add_weight(shape=(1, n_questions), initializer='ones', trainable=True)
self.b = self.add_weight(shape=(1, n_questions), initializer='zeros', trainable=True)
def call(self, x):
"""
x (tf.Tensor): 能力値 with shape (n_batch, 1)
"""
return 1/(1 + tf.exp(-self.a*(x - self.b)))
class IRTModel(tf.keras.Model):
def __init__(self, n_students, n_questions, **kwargs):
super().__init__(self, **kwargs)
self.n_students = n_students
self.n_questions = n_questions
# 標準正規分布を初期値とする
self.theta = tf.keras.layers.Embedding(n_students, 1, embeddings_initializer='zeros')
self.irt = IRT2PLLayer(n_questions)
def call(self, x):
"""
x (tf.Tensor): 受験者ID with shape (n_batch, 1)
"""
theta = self.theta(x)
return self.irt(theta)
ここで、
model.compile(
loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=['binary_accuracy']
)
# 適当に受験者のindexを振っておく(ここでは 0, 1, .... となる)
train_x = np.arange(train_df.shape[0])[:, np.newaxis]
# train_dfから Student ID カラムを除いたもの
train_y = train_df.values[:, 1:].astype(np.float64)
model.fit(train_x, train_y, batch_size=1, epochs=100)
...
Epoch 99/100
214/214 [==============================] - 0s 387us/step - loss: 0.5953 - binary_accuracy: 0.6818
Epoch 100/100
214/214 [==============================] - 0s 347us/step - loss: 0.5953 - binary_accuracy: 0.6818
何度か実験した結果、バッチサイズが大きいと収束しづらいことがわかったので、小さくしています。平均正答率 0.42 なので、全て
念の為に、横軸に各設問の正答率、縦軸に推定された困難度
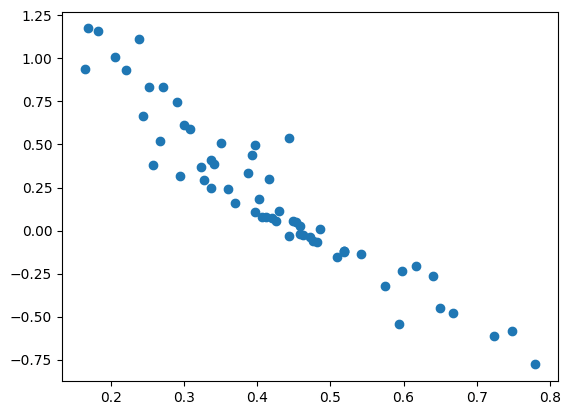
正答率の低い(高い)設問ほど困難度が高い(低い)ことがわかります。次に、能力値
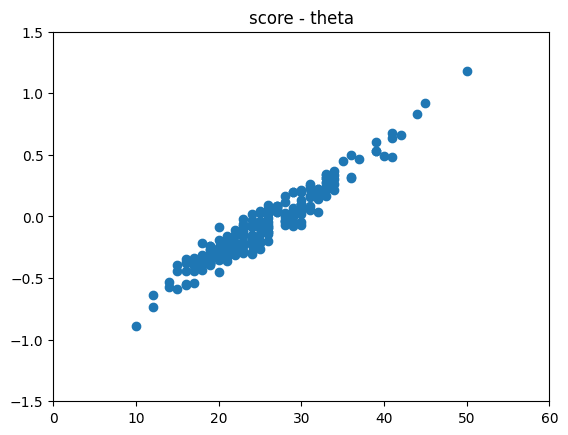
得点が高いほど能力値
当然ですが、受験者によっては自分より得点が低い受験者に能力値で負けるようなケースがあります。
項目パラメーターを固定して 能力値を推定する
上で推定された項目パラメーターが、新しい受験者に対しても有効か、検証データを使って検証してみましょう。それには、新しく項目パラメーターを固定したモデルを用意して能力値
# 訓練データと検証データでは受験者数が異なるので、新たにモデルを作る
model_for_test = IRTModel(n_students, n_questions)
# 訓練済みの項目パラメーターをセットして、訓練対象から外す
model_for_test.irt.set_weights(model.irt.get_weights())
model_for_test.irt.trainable = False
model_for_test.compile(
loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=['binary_accuracy']
)
test_x = np.arange(test_df.shape[0])[:, np.newaxis]
test_y = test_df.values[:, 1:].astype(np.float64)
model_for_test.fit(test_x, test_y, batch_size=1, epochs=100)
...
Epoch 99/100
24/24 [==============================] - 0s 471us/step - loss: 0.6045 - binary_accuracy: 0.6576
Epoch 100/100
24/24 [==============================] - 0s 426us/step - loss: 0.6044 - binary_accuracy: 0.6576
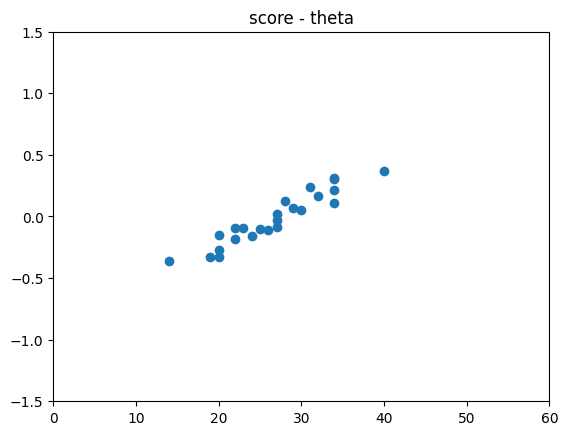
binary_accuracy は 0.6576 で、訓練データの 0.6818 とは乖離がありますが、おかしなことにはなっていなさそうです。得点と能力値のプロットは以下の通りです。訓練セットと違って低得点・高得点の受験者が含まれていなかったようで、少し微妙ですが、ここでは深掘りしないことにします。
AutoEncoder としての実装
ここまでで、
- 項目パラメーターの推定
- 項目パラメーターを固定して、新たな受験者の能力パラメーターを推定
の2つができるようになったので、
- プレテストで項目パラメーターを推定しする
- 問題を解く毎に能力値を推定し直す
- 推定した能力値で最も項目情報量の大きい問題を出す
という手順でCATは実現できそうです。
ただ、上の方法では、問題を解く毎に能力パラメーターが収束するまで最適化計算(上記のコードでいうfitメソッド)を回す必要があります。最適化計算にはある程度計算量が必要ですが、問題を解く毎に待たされるようではユーザー体験が良くありません[10]。
そこで、それまでの解答結果から能力値
- それまでの解答結果を受け取り能力値を出力するモデル
- 能力値からそれぞれの問題の正答確率を出力するモデル
の2つを作り、つなげるということです。これは潜在空間の次元数が 1 の AutoEncoder に他なりません。
Keras で encoder を実装してみると、以下のようになりました。CATでの利用を想定しているので、未解答の問題があっても正常に推論できるよう、以下の工夫しています。
- 未解答の問題をマスキングできるようにしておく
-
LocallyConnected1DやConv1Dを使って、問題毎に推定値を求め、それを集約するような構造にする- 問題同士の交互作用をモデル化してしまうと、問題をマスクされた場合に正常に動作させるのが大変そうなので
class IRTEncoder(tf.keras.Model):
def __init__(self, n_questions, **kwargs):
super().__init__(self, **kwargs)
self.n_questions = n_questions
# CATへの応用を考え、Mask可能にしておく(入力値が -1 の項目については無視する)
self.mask = tf.keras.layers.Masking(mask_value=-1)
self.feature_extractors = (
tf.keras.layers.LocallyConnected1D(8, 1, activation='relu'),
tf.keras.layers.Conv1D(4, 1, activation='relu')
)
self.pooling = tf.keras.layers.GlobalAvgPool1D()
self.get_output = tf.keras.layers.Dense(1)
def call(self, inputs, mask=None):
x = inputs
if mask is None:
x = self.mask(x)
mask = x._keras_mask
for layer in self.feature_extractors:
x = layer(x)
x = self.pooling(x, mask=mask)
x = self.get_output(x)
return x
decoder は、これまでのモデルから、IRT2PLLayer そのもの)です
class IRTDecoder(tf.keras.Model):
def __init__(self, n_questions, **kwargs):
super().__init__(self, **kwargs)
self.n_questions = n_questions
self.irt = IRT2PLLayer(n_questions)
def call(self, x):
return self.irt(x)
これらを組み合わせると、AutoEncoder になります。
class IRTAutoEncoder(tf.keras.Model):
def __init__(self, encoder, decoder, **kwargs):
super().__init__(self, **kwargs)
self.encoder = encoder
self.decoder = decoder
def call(self, inputs):
return self.decoder(self.encoder(inputs))
訓練します。これまでと違い、訓練しながら検証データにおける精度指標を確認できます。
train_x = train_df.values[:, 1:, np.newaxis].astype(np.float32)
test_x = test_df.values[:, 1:, np.newaxis].astype(np.float32)
auto_encoder.fit(train_x, train_x, validation_data=(test_x, test_x), batch_size=1, epochs=100)
...
Epoch 99/100
214/214 [==============================] - 0s 597us/step - loss: 0.5957 - binary_accuracy: 0.6827 - val_loss: 0.6033 - val_binary_accuracy: 0.6625
Epoch 100/100
214/214 [==============================] - 0s 596us/step - loss: 0.5957 - binary_accuracy: 0.6815 - val_loss: 0.6030 - val_binary_accuracy: 0.6653
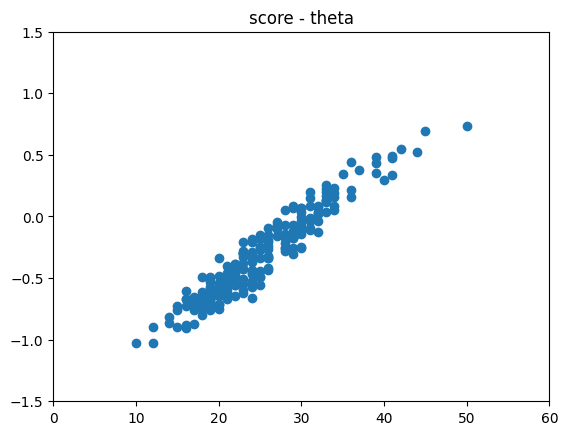
訓練データでの binary_accuracy は埋め込みモデルと同等、検証データでの binary_accuracy は埋め込みモデルよりも高いようです。訓練データに対する得点と能力値のプロットは以下の通りです。埋め込みモデルの場合と少し分布が違いそうですが、傾向は大体合っていそうです。
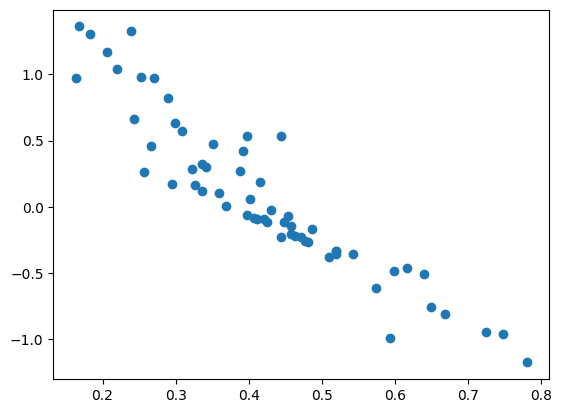
正答率と困難度のプロットは以下のとおりです。こちらは、埋め込みモデルとかなり似た分布になりました。
解答数が少ない場合に推定値がどうなるかも確認しておきましょう。以下の図は横軸に全問解答した時の能力値の推定値、縦軸に試験の
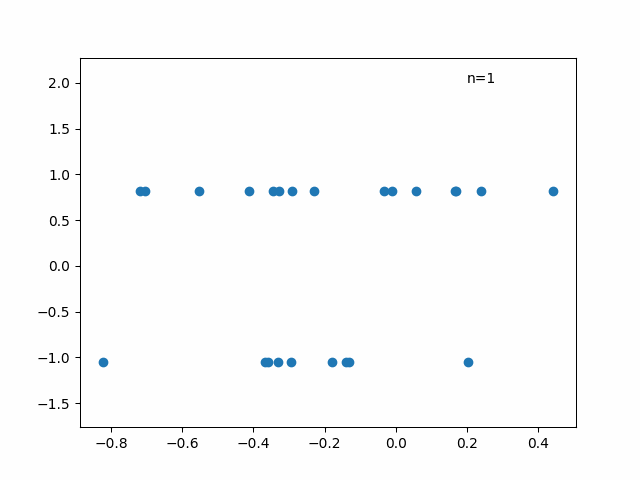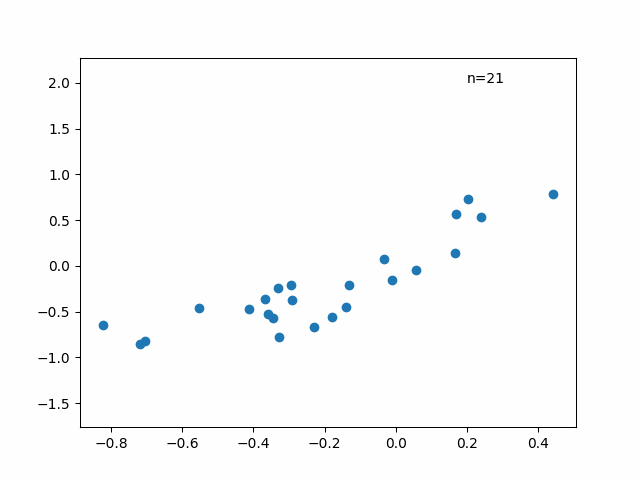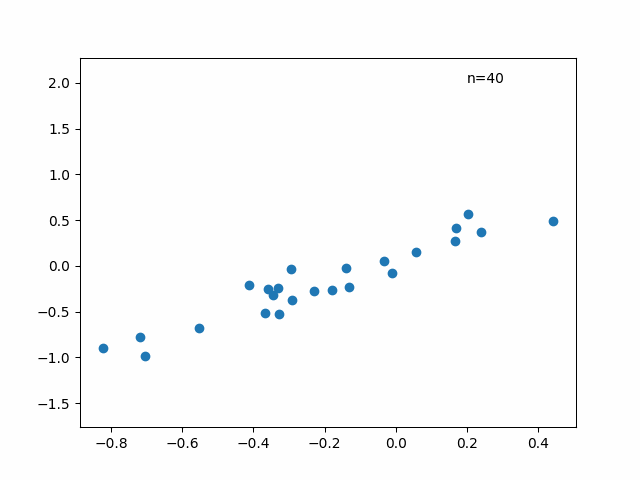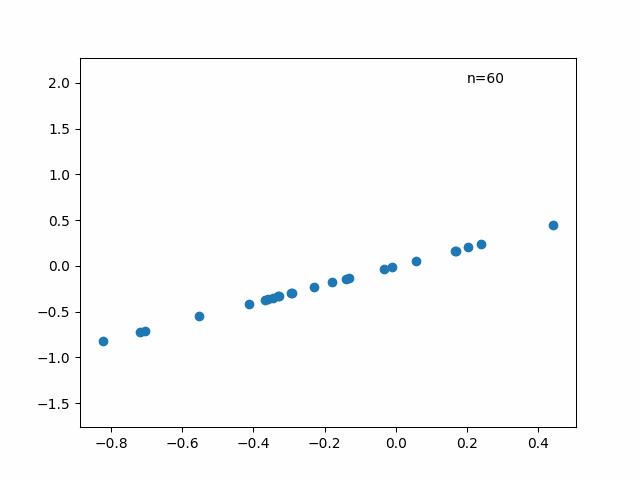
CATの実装
では、訓練済みの AutoEncoder を使ってCATを実装してみましょう。
CAT では項目情報量が最大となる問題を選択するので、訓練済みの IRT2PLLayer から項目情報関数を返す関数を定義しておきます。
def get_iif(irt):
"""
Parameters:
irt (IRT2PLLayer): 対象となる項目パラメーターを含む IRT2PLLayer
Returns:
iif (Callable[[float], float]): 項目情報関数. 能力値を受け取り、項目情報量を返す
"""
def iif(inputs):
a = irt.a
p = irt(inputs)
q = 1 - p
return (a*a*p*q).numpy()
return iif
念の為に、設問を一つ選んで正答確率と項目情報量をプロットすると以下のようになりました。うまく動いていそうです。
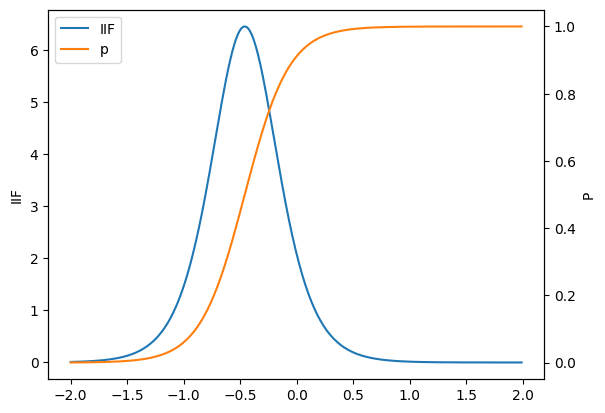
与えられた
# 例えば theta = 0.5 の場合
theta = 0.5
best_item = iif(theta).argmax()
これを Encoder と組み合わせれば CAT として動くものができます。本来は、なんらかの停止条件(その時点での試験情報量や設問数など)を定義するとよいでしょう。
def select_next(responses):
"""
Parameters:
responses (np.ndarray): それまでの解答履歴. 未解答の設問については -1. (batch_size=1, n_questions, 1)
Returns:
next_item (int): 次に出題すべき問題のインデックス
log (dict): シミュレーション用のログ
"""
# 1問も解いていない場合は theta に適当な値をセットする
if (responses == -1).all():
theta = 0.
else:
theta = encoder.predict(responses)
ii = iif(theta)
# 選択済みの問題: mask = 0, 未選択の問題: mask = 1
mask = (responses == -1).astype(int).flatten()
# 出題済みの問題をマスクして次の問題を選択
next_item = (ii*mask).flatten().argmax()
# 出題済みの問題についての試験情報量. ログのためだけに計算
ti = (ii*(1-mask)).sum()
log = {
'theta': theta,
'ii': ii.max(),
'ti': ti,
'item': next_item
}
return next_item, log
検証データを用いてシミュレーションを行い、出題数毎の試験情報量の平均値をプロットしたところ、以下のようになりました。縦軸は(最終的な能力値ではなく)その時点での能力値
なお、今回のデーセットでは項目プールが60題しかないため、最終的にはランダムな場合とCATで試験情報量が一致します。項目プールを増やすことで、ランダムとCATとの差はより顕著になるはずです。

シミュレーションコード
def simulate_cat(all_responses):
"""
Arguments:
all_responses (np.ndarray): 全ての設問に対する解答. (batch_size=1, n_questions, 1)
Returns:
histry (list): シミュレーションログ
"""
n_questions = all_responses.shape[1]
# シミュレーションの中での解答履歴. 初めは1問も解答していないので、全て -1
responses = -1 * np.ones_like(all_responses)
history = []
for i in np.arange(n_questions):
item, log = select_next(responses)
responses[:, item, :] = all_responses[:, item, :]
log['iter'] = i
history.append(log)
return history
histories = []
for response in test_x:
history = simulate_cat(response[np.newaxis])
irt_histories.append(history)
まとめと展望
受験者毎に最適化された問題が出題される試験(CAT)の仕組みを調べ、実装しました。
CAT の裏側では項目反応理論と呼ばれる理論が利用されており、その仕組みは、能力値を潜在空間として持つ AutoEncoder とみなして実装できるものでした。
項目反応理論で推定される能力値は、モデルや推定方法によって変わるため、公平性の強く要求される試験での導入は難しそうだなと思った一方、(他人との比較ではなく)個人の能力を把握したい場合には有用だなと感じました。
今回は、シンプルな AutoEncoder を実装して検証しましたが、以下のような改善を考えられそうです。特にベイズ化や多腕バンディット化は面白そうなので、時間を見つけて Pyro/NumPyro あたりで実装してみようと思います。
- AutoEncoderの訓練方法の改善
今回は全ての解答結果を入力として使っており、解答数が少ない場合にも良いモデルになっているかは不透明です。CATへの応用という観点では、入力する回答結果をランダムにマスクするなどの工夫が考えられます - 埋め込み空間の多次元化
今回は AutoEncoder の潜在空間を1次元としましたが、2次元以上にすることも考えられます。これは多次元項目反応理論に対応します - 適切な評価指標の策定
試験の良さとして試験情報量を用いましたが、「よい試験 = 能力値を誤差少なく推定できる = その試験で推定された能力値で、解答結果をよく説明できる」と考えると、試験情報量ではなく、モデルの cross entropy や accuracy を指標としてもよさそうです。 - 多様なデータセットでの評価
現時点では1つのデータセットで評価してみただけなので、他のデータセットでも同様のことができるのかがわかりません。 - AutoEncoder の VAE化/ベイズ化
試験の良さを試験情報量で評価していましたが、試験情報量は「能力値の推定値の誤差」の指標であることを考えると、ベイズ化して分散を含めて推定できれば、もっと自然な構成になりそうです。 - 多腕バンディットとしての定式化
標準的な CATでは、プレテストで項目パラメーターを推定しますが、項目プールを増やしたいことを考えると、問題を逐次的に追加できるようにできると嬉しいです。それには、プレテストではなくCATの試験中に項目パラメーターを推定するための設問を追加すればよいでしょう。\epsilon
参考文献
- 加藤 健太郎, 山田 剛史, 川端 一光(2014). 『Rによる項目反応理論』. オーム社.
- 項目反応理論やってみよう (参照 2023/01/06)
-
もうちょっと見方を変えて(襷掛け云々ではなく)疎なロジスティック回帰そのものとみなすこともできます ↩︎
-
項目反応理論では
\theta_a \beta_i -
2パラメーターモデルにおける
P(u_{a,i} = 1|\theta_{a}, \alpha_{i}, \beta_{i}) \theta_a = \beta_i 0.5 -
試験情報量が試験の良さを表すには、問題同士が違いに条件付き独立であることが重要です.例えば、同じ問題を2問出すと、項目情報量の和である試験情報量も増えてしまいますが、テストが良くなったわけではありません ↩︎
-
普通の試験では「合計得点が高い = 能力が高い」と考え、合計得点によって能力値の代替としている、と考えることができます ↩︎
-
この方法は同時最尤推定法と呼ばれることが多いようです ↩︎
-
Rによる項目反応理論 P. 176 ↩︎
-
設問に紐づくパラメーター(困難度と識別力)と受験者に紐づくパラメーター(能力値)の両方を同時に推定する同時最尤推定、受験者に紐づくパラメーターを周辺化して設問に紐づくパラメーターを推定する周辺最尤推定、MAP推定、EAP推定、ベイズ予測(変分法、MCMC)など ↩︎
-
ニューラルネットワークやKerasにこだわらないのであれば、 Newton-Raphson 法を使うと一瞬で解けます。 ↩︎
Discussion