Zenn
🍎

Juliaで学ぶLangevin方程式

2022/09/30に公開
Julia
math
#
数値計算
#
物理
#
sde
tech


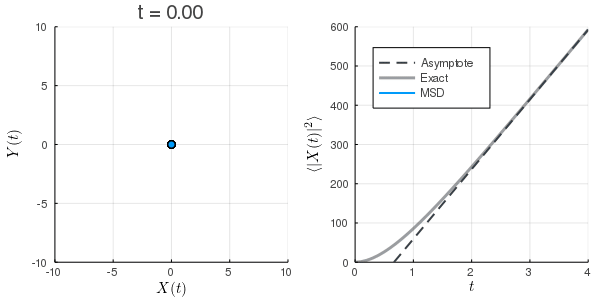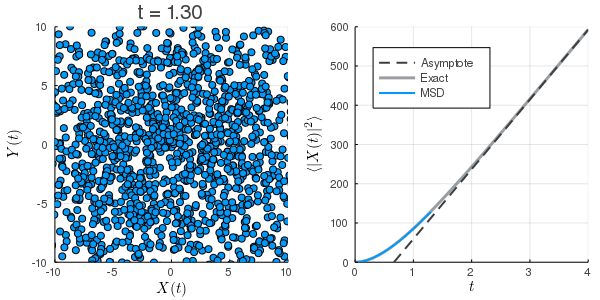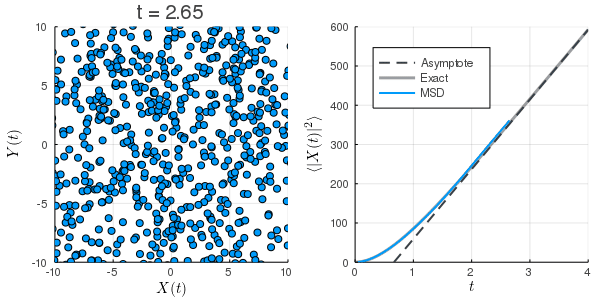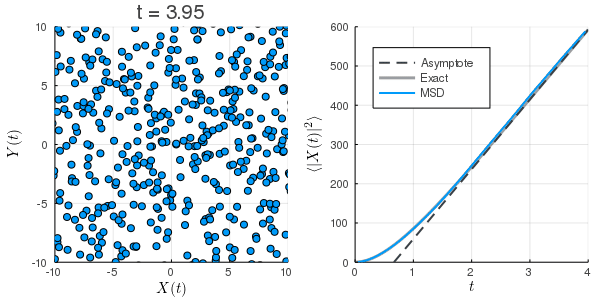
このノートではJulia言語を用いてLangevin方程式の数値計算を行い, 北原和夫『岩波基礎物理シリーズ 8 非平衡系の統計力学』(岩波書店, 1997)から平均二乗変位の式を援用し, 計算結果の評価を行う. 頑なに揺動力の強さD_uと拡散係数Dを区別する理由は, 拡散係数を求める際によく目にする\langle|X(t)|^2\rangle = 2nDtとLangevin方程式から導かれる\langle|\boldsymbol{X}(t)|^2\rangle = 2n\frac{D_u m}{\gamma^3} \left(\frac{\gamma}{m} t+e^{-\frac{\gamma}{m} t}-1 \right)を勘違いしないためである.

パッケージ

可視化にはPlots.jlを用いる. Plots.jlの入門的内容はこちらのノートを参照されたい. plot()を使用するためには, Juliaのパッケージモードでadd Plotsを実行し, 事前にPlots.jlをインストールしておく必要がある. ノート上ではusing Plotsを宣言する. また, using Printfも宣言するが, 標準ライブラリであるためインストールは不要である.

入力
versioninfo()
# using Pkg
# Pkg.add("Plots")
using Plots
using Printf
出力
    Julia Version 1.6.2
    Commit 1b93d53fc4 (2021-07-14 15:36 UTC)
    Platform Info:
      OS: Windows (x86_64-w64-mingw32)
      CPU: Intel(R) Core(TM) i7-4650U CPU @ 1.70GHz
      WORD_SIZE: 64
      LIBM: libopenlibm
      LLVM: libLLVM-11.0.1 (ORCJIT, haswell)

Langevin方程式

Langevin(1908)で与えられたLangevin方程式は次式である.

m\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -6\pi\mu a \frac{\mathrm{d} x}{\mathrm{d}t} + X \tag{3}

LangevinがLangevin(1908)で与えたLangevin方程式は, Stokesの式\gamma=6\pi\mu aと速度V(t):=\mathrm{d}X(t)/\mathrm{d}tの定義を使って以下のように書き直せる.

\begin{aligned} \frac{\mathrm{d} X(t)}{\mathrm{d}t} &= V(t) \\ m\frac{\mathrm{d} V(t)}{\mathrm{d}t} &= -\gamma V(t) + R(t) \end{aligned}

速度V(t)の方程式はOrnstein–Uhlenbeck過程として解釈できる.

平均二乗変位

北原和夫『岩波基礎物理シリーズ 8 非平衡系の統計力学』(岩波書店, 1997)はp.90の式(4.38)

m\frac{\mathrm{d}\boldsymbol{u}}{\mathrm{d}t} = -m\gamma\boldsymbol{u} + \boldsymbol{R}(t) \tag{4.38}

を出発点とし, p.94の式(4.59)の平均二乗変位を導出している.

\langle|\boldsymbol{x}(t)|^2\rangle = \frac{6k_\mathrm{B}T}{m\gamma^2}(\gamma t+e^{-\gamma t}-1) \tag{4.59}

式(4.59)を援用するが, 出発点となる方程式が異なるので, そのままでは上記の計算の検証には使えない.

注意点

注意すべき点を述べておく. 北原和夫『岩波基礎物理シリーズ 8 非平衡系の統計力学』(岩波書店, 1997) p.90の式(4.38)や北原和夫『講談社基礎物理学シリーズ 8 統計力学』(講談社サイエンティフィク, 2010) p.192の式(12.24)では粘性抵抗を-m\gamma\boldsymbol{u}としており, 質量に比例するものとしている. 出発点が異なるため, 平均二乗変位の式(4.59)もそのままではLangevin(1908)の検証には使えない.

この流儀を採用した意図はわからないが, Einsteinの関係式(揺動散逸定理)における質量の寄与を明示的に扱える利点が挙げられる. 粘性抵抗の係数\gammaは物体の形状(球ならば半径)のみによって決定されるが, 体積が大きいほど質量も大きくなるので, 間接的には質量にも依存しているから, それを明示的に示すためだったのかもしれない.

\gamma'=m\gamma, D_u=m\gamma k_\mathrm{B}T=\gamma' k_\mathrm{B}Tとし, さらにn次元の場合(6\rightarrow2n)を考えると

\langle\|\boldsymbol{X}(t)\|^2\rangle = 2n\frac{D_u m}{\gamma'^3} \left(\frac{\gamma'}{m} t+e^{-\frac{\gamma'}{m} t}-1 \right)

となる. これを用いて, Langevin方程式の数値計算の結果を評価する. また, 熱平衡状態を初期値として仮定しているため, 最初に位置は変化させずに速度だけでBrown運動の計算を行っておく必要がある.

数値計算

離散化

速度V(t)の方程式にはEular-Maruyama法を, 変位X(t)の方程式には通常のEular法を使うとうまくいく.

\begin{aligned} X_{i+1} \simeq X_i + V_i\Delta t\\ V_{i+1} \simeq V_i - \frac{\gamma}{m}\Delta t + \frac{1}{m}\Delta W_i \end{aligned}

このようにしてBrown運動の軌道を計算できる. しかし, 何を以てこの計算の妥当性を評価するかという問題がある. Ornstein–Uhlenbeck過程のP(v,t)は既に明らかになっているが, P(x,t)を求めるのは難しそうである. その代わりに, 平均二乗変位を用いて計算の妥当性を評価する.

初速0の場合

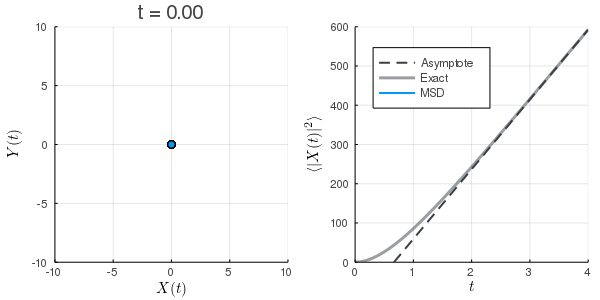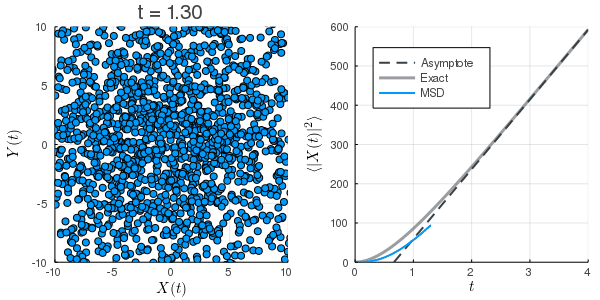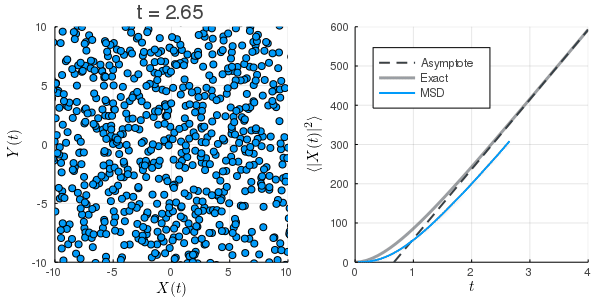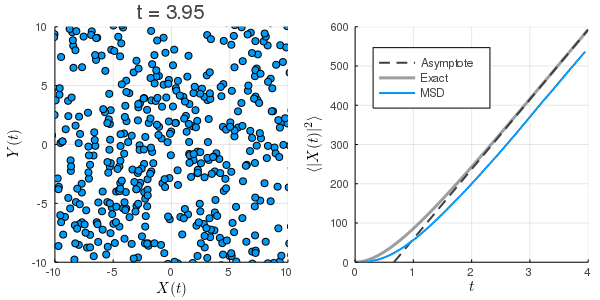
初期条件が熱平衡になっていないため, MSDが小さくなっている.

#概要：2次元のLangevin方程式mx"(t)=-γx'(t)+R(t)の平均二乗変位
#環境：Windows 10 Pro x64 (i7-4650U, 8.00GB)
#言語：Julia (Version 1.0.2)
#作成：2019-09-16
#更新：2021-08-26

function MSD_nonequilibrium()
    # パラメータ：
    i_max = 80               # 時間ステップ
    N  = 2000                # 粒子数
    m  = 0.1                 # 質量
    Du = 1.0                 # 揺動力の強さ(拡散係数Dではない)
    γ = 0.15                # 粘性抵抗の強さ
    dt = 0.05                # 時間刻み幅
    T = fill(NaN,i_max)
    MSD = fill(NaN,i_max)
    anim = Animation()

    # 初期値：
    t = 0.0
    X = zeros(N)
    Y = zeros(N)
    U = zeros(N)
    V = zeros(N)
    # for i in 1:i_max
    #     U = U - γ/m*U*dt + 1/m*sqrt(2*Du*dt)*randn(N) # 熱平衡化
    #     V = V - γ/m*V*dt + 1/m*sqrt(2*Du*dt)*randn(N) # 熱平衡化
    # end
    T[1] = t
    MSD[1] = (sum(X.^2) + sum(Y.^2))/N

    # 実行：
    for i in 1:i_max
        # 描写：
        plt1 = scatter(X, Y, xlims=(-10,10), ylims=(-10,10), label="", xlabel="\$X(t)\$", ylabel="\$Y(t)\$", title=@sprintf("t = %.2f",t))
        plt2 = plot(0:0.1:4, t->4*Du*m/(γ^3)*(γ/m*t             -1), xlim=(0,4), ylim=(0,600), label="Asymptote", lc="#393e46", lw=2, ls=:dash)
        plot!(plt2, 0:0.1:4, t->4*Du*m/(γ^3)*(γ/m*t+exp(-γ/m*t)-1), xlim=(0,4), ylim=(0,600), label="Exact", lc="#393e46", lw=3, la=0.5)
        plot!(plt2, T, MSD, label="MSD", xlabel="\$t\$", ylabel="\$\\langle |X(t)|^2 \\rangle\$", lc=1, lw=2, legend=:topleft)
        frame(anim, plot(plt1, plt2, size=(600,300)))
        # 計算：
        t = t + dt
        U = U - γ/m*U*dt + 1/m*sqrt(2*Du*dt)*randn(N)
        V = V - γ/m*V*dt + 1/m*sqrt(2*Du*dt)*randn(N)
        X = X + U*dt
        Y = Y + V*dt
        T[i] = t
        MSD[i] = (sum(X.^2) + sum(Y.^2))/N
    end
    gif(anim, "MSD_nonequilibrium.gif", fps = 15)
end

MSD_nonequilibrium()

熱平衡状態

計算の前に, 位置を固定したまま速度U(t), V(t)のみの時間発展を適当な長さだけ計算しておき, 熱平衡状態を作ることができる. 正しく熱平衡状態を初期条件としたため, 解析的に求めたMSDに一致している.

#概要：2次元のLangevin方程式mx"(t)=-γx'(t)+R(t)の平均二乗変位
#環境：Windows 10 Pro x64 (i7-4650U, 8.00GB)
#言語：Julia (Version 1.0.2)
#作成：2019-09-16
#更新：2021-08-26

function MSD()
    # パラメータ：
    i_max = 80               # 時間ステップ
    N  = 2000                # 粒子数
    m  = 0.1                 # 質量
    Du = 1.0                 # 揺動力の強さ(拡散係数Dではない)
    γ = 0.15                # 粘性抵抗の強さ
    dt = 0.05                # 時間刻み幅
    T = fill(NaN,i_max)
    MSD = fill(NaN,i_max)
    anim = Animation()

    # 初期値：
    t = 0.0
    X = zeros(N)
    Y = zeros(N)
    U = zeros(N)
    V = zeros(N)
    for i in 1:i_max
        U = U - γ/m*U*dt + 1/m*sqrt(2*Du*dt)*randn(N) # 熱平衡化
        V = V - γ/m*V*dt + 1/m*sqrt(2*Du*dt)*randn(N) # 熱平衡化
    end
    T[1] = t
    MSD[1] = (sum(X.^2) + sum(Y.^2))/N

    # 実行：
    for i in 1:i_max
        # 描写：
        plt1 = scatter(X, Y, xlims=(-10,10), ylims=(-10,10), label="", xlabel="\$X(t)\$", ylabel="\$Y(t)\$", title=@sprintf("t = %.2f",t))
        plt2 = plot(0:0.1:4, t->4*Du*m/(γ^3)*(γ/m*t             -1), xlim=(0,4), ylim=(0,600), label="Asymptote", lc="#393e46", lw=2, ls=:dash)
        plot!(plt2, 0:0.1:4, t->4*Du*m/(γ^3)*(γ/m*t+exp(-γ/m*t)-1), xlim=(0,4), ylim=(0,600), label="Exact", lc="#393e46", lw=3, la=0.5)
        plot!(plt2, T, MSD, label="MSD", xlabel="\$t\$", ylabel="\$\\langle |X(t)|^2 \\rangle\$", lc=1, lw=2, legend=:topleft)
        frame(anim, plot(plt1, plt2, size=(600,300)))
        # 計算：
        t = t + dt
        U = U - γ/m*U*dt + 1/m*sqrt(2*Du*dt)*randn(N)
        V = V - γ/m*V*dt + 1/m*sqrt(2*Du*dt)*randn(N)
        X = X + U*dt
        Y = Y + V*dt
        T[i] = t
        MSD[i] = (sum(X.^2) + sum(Y.^2))/N
    end
    gif(anim, "MSD.gif", fps = 15)
end

MSD()

まとめ

Eular-Maruyama法に基づいたLangevin方程式の離散化と数値計算の方法を解説した. 熱平衡状態を初期条件として計算を行ったところ, 北原和夫『岩波基礎物理シリーズ 8 非平衡系の統計力学』(岩波書店, 1997)に適切な修正を加えたMSDと一致する結果が得られた.

参考文献

この記事は2021年10月23日(土)に行われた第8回 ぶつりがく徒のつどい の講演資料を元に改良を加えたものです. 記事の元になったノートはGistにアップロードしてあります.

https://gist.github.com/ohno/0a832b077099022c41f2ac678019554d

Discussion