🍊

Juliaで学ぶ確率微分方程式

2022/09/30に公開

Julia

Julia言語の疑似乱数にはdSFMTが採用されており, 特別な準備をせずに良質な疑似乱数を用いて計算を行うことができるため, 確率微分方程式（Stochastic Differential Equation, SDE）との相性が極めて良い. この記事では, 確率過程の概念, Eular-Maruyama法による種々の確率微分方程式の数値解法について, Julia言語での実装例を交えて解説する. 得られた数値解はPlots.jlを用いて可視化し, Fokker-Planck方程式の解析解と比較する.

パッケージ

可視化にはPlots.jlを用いる. Plots.jlの入門的内容はこちらのノートを参照されたい. plot()を使用するためには, Juliaのパッケージモードでadd Plotsを実行し, 事前にPlots.jlをインストールしておく必要がある. ノート上ではusing Plotsを宣言する. また, using Printfも宣言するが, 標準ライブラリであるためインストールは不要である.

versioninfo()
# using Pkg
# Pkg.add("Plots")
using Plots
using Printf

出力

    Julia Version 1.6.2
    Commit 1b93d53fc4 (2021-07-14 15:36 UTC)
    Platform Info:
      OS: Windows (x86_64-w64-mingw32)
      CPU: Intel(R) Core(TM) i7-4650U CPU @ 1.70GHz
      WORD_SIZE: 64
      LIBM: libopenlibm
      LLVM: libLLVM-11.0.1 (ORCJIT, haswell)

確率過程

確率過程（stochastic process）とは, 時間に依存して変化する確率変数（stochastic variable）のことである. 時間が $t=1,2,3,4,\cdots$ のように離散的な値をとる確率過程を離散確率過程（discrete stochastic process）といい, 連続的な値をとる確率過程を連続確率過程（containuous stochastic process）という.

いい加減な定義ではあるものの, 確率変数が $X:\Omega\rightarrow\mathbb{R^n}$ であり, 確率過程が $X:\Omega\times T\rightarrow\mathbb{R^n}$ であるから, 概ね正しいと思われる.

このノートでは, 離散確率過程の例としてランダムウォークモデルを, 連続確率過程の例としてWiener過程(数学ではBrown運動と呼ぶことがある), ドラフト項のあるWiener過程, Ornstein–Uhlenbeck過程などのを取り上げる. これらの連続確率過程は確率微分方程式（Stochastic Differential Equation, SDE）の解でもある.

ランダムウォークモデル

よく勘違いされるが, ランダムウォークモデルとWiener過程(数学ではBrown運動と呼ぶことがある)は別のモデルであり, 前者は離散確率過程で後者は連続確率過程である. ここでは, 離散確率過程の例としてランダムウォークモデルを取り上げる.

先に補足しておくと, ランダムウォークモデルの連続極限として拡散方程式を導出できる（付録参照）. Wiener過程もその確率密度関数の時間発展が拡散方程式(Fokker-Planck方程式の特殊化)で記述されることから, これらの対応関係を知っておくことは学習の役に立つと思われる.

コインを投げて表なら $R_i=+1$ , 裏なら $R_i=-1$ を得点とする. コインを $i$ 回目に投げたときの合計得点を $X_i=\sum_{j=1}^{i}R_j$ とする. $i=1$ のとき, $X_i=+1,-1$ のどちらかだが, $i=2$ の時は $X_i=+2,0,-2$ のどれかの値を取りうる. つまり, 確率分布が時間 $i$ に依存する. なお, $R_i$ の確率分布は時間に依らない.

以下に, 横軸を投げた回数 $i$ とし, 縦軸をそれぞれ得点 $R_i$ と合計得点数 $X_i$ としたグラフを描写した.

step = 30

R = Int.((floor.(rand(step)*2) .- 0.5)*2)
X = zeros(Int64, step)

X[1] = R[1]
for i in 2:step
    X[i] = X[i-1] + R[i]
end

println("R = ", R)
println("X = ", X)

plot(
    plot(R, xlabel="\$i\$", ylabel="\$R_i\$", label=""),
    plot(X, xlabel="\$i\$", ylabel="\$X_i\$", label=""),
    size=(600, 300),
    fmt=:png
)

savefig("randomwalk.png")
plot!()

出力

    R = [-1, 1, -1, 1, -1, 1, 1, 1, -1, 1, 1, -1, 1, -1, -1, 1, -1, 1, -1, 1, 1, 1, 1, 1, 1, -1, 1, -1, 1, -1]
    X = [-1, 0, -1, 0, -1, 0, 1, 2, 1, 2, 3, 2, 3, 2, 1, 2, 1, 2, 1, 2, 3, 4, 5, 6, 7, 6, 7, 6, 7, 6]

また, 500人でランダムウォーク大会を行った場合のグラフと, それぞれの $i$ について人数を数えたヒストグラムを示した. 十分に試行回数が増えればガウス分布に近づくはずである.

step = 30
member = 500

R = (floor.(rand(step, member)*2) .- 0.5)*2
X = zeros(step, member)

X[1,:] = R[1,:]
for i in 2:step
    X[i,:] = X[i-1,:] + R[i,:]
end

plt1 = plot(R, alpha=0.2, label="", xlabel="\$i\$", ylabel="\$R_i\$", legend=:topleft) 
plot!(plt1, 1:step, i->1, color=:red, label="Max ") 
plot!(plt1, 1:step, i->-1, color=:blue, label="Min")

plt2 = plot(X, alpha=0.2, label="", xlabel="\$i\$", ylabel="\$X_i\$", legend=:topleft) 
plot!(plt2, 1:step, i->i, color=:red, label="Max ") 
plot!(plt2, 1:step, i->-i, color=:blue, label="Min")

plot(plt1, plt2, size=(600, 300), fmt=:png)
savefig("randomwalks.png")
plot!()

plt = []
for i in 1:12
    push!(plt, histogram(X[i,:], title="i=$i", bins=range(-1.1*i,1.1*i,step=0.1), label=""))
end

plot(plt...)

savefig("randomwalks_histogram.svg")
plot!()

白色雑音とWiener過程

正確ではないが, 白色雑音 $R(t)$ はWiener過程 $W(t)$ の時間微分のようなものであり, ちょうどコインを投げた回数 $i$ に対する, 得点 $R_i$ と合計得点数 $X_i$ の関係によく似たものである.

step = 1000
Du = 1.5
dt = 0.01

T = [dt*i for i in 0:step-1]
W = zeros(step)
dW = sqrt(2*Du*dt)*randn(step)

for i in 2:step
    W[i] = W[i-1] + dW[i]
end

plot(
    plot(T, dW, xlabel="\$i\\Delta t\$", ylabel="\$\\Delta W_i\$", label=""),
    plot(T, W, xlabel="\$i\\Delta t\$", ylabel="\$W_i\$", label=""),
    size=(600, 300),
    fmt=:png
)

savefig("wiener_process.png")
plot!()

step = 1000
member = 200
Du = 1.5
dt = 0.01

T = [dt*i for i in 0:step-1]
W = zeros(step, member)
dW = sqrt(2*Du*dt)*randn(step, member)

for i in 2:step
    W[i,:] = W[i-1,:] + dW[i,:]
end

plot(
    plot(T, dW, xlabel="\$i\\Delta t\$", ylabel="\$\\Delta W_i\$", label="", lw=1, la=0.1, lc=[1 2 3 4 5 6 7 8 9 10]),
    plot(T, W, xlabel="\$i\\Delta t\$", ylabel="\$W_i\$", label="", lw=1, la=0.1, lc=[1 2 3 4 5 6 7 8 9 10]),
    size=(600, 300),
    fmt=:png
)

savefig("wiener_processes.png")
plot!()

Langevin方程式を扱う物理学の文脈では, 白色雑音は揺動力として導入され, その性質を出発点とした相関関数の計算によって議論が進められる. 一方, 数学では白色雑音の扱いを避けて, Wiener過程を議論の出発点に採用することが多いようである(理由は後述する).

このノートでも, 白色雑音の性質は不要なので使わない. また, Wiener過程についても $W(t)-W(s) \sim N(0,2D_u(t-s))$ という性質を使うのみなので, どちらも簡単な紹介に留める. 白色雑音 $R(t)$ とWiener過程 $W(t)$ はそれぞれ次のような性質を満たすものとして定義されることが多い.

\begin{aligned} \langle R(t) \rangle &= 0\\ \langle R(t_1)R(t_2) \rangle &= 2D_u \delta(t_1-t_2)\\ \\ \langle W(t) \rangle &= 0\\ \langle W(t_1)W(t_2) \rangle &= 2D_u {\rm min}(t_1,t_2)\\ W(t) &\sim N(0,t) \end{aligned}

なお, $X \sim N(\mu,\sigma^2)$ は確率変数 $X$ が平均 $\mu$ , 分散 $\sigma^2$ の正規分布に従うという意味である. Wiener過程 $W(t)$ の最も重要な性質は

W(t)-W(s) \sim N(0,2D_u(t-s))

である. 兼清(2017) p.103ではこの性質をWiener過程 $W(t)$ の定義に含めているが, 三井(2004) p.139では定理として導出している. いずれにせよ, この性質によって, Wiener過程 $W(t)$ を時間間隔 $\Delta t$ で分割するとき, $\Delta t$ あたりの変化量 $\Delta W$ が正規分布 $N(0,2D_u\Delta t)$ に従う疑似乱数として計算できる. ここで述べていることはEular-Maruyama法の特殊例であるから, 厳密な議論を必要とする読者はIto-Taylor展開によるEular-Maruyama法の導出について参照されたい.

step = 10
dt = 0.01
# Du = 1.5

# T = [dt*i for i in 0:step-1]
# W = zeros(step)
# dW = sqrt(2*Du*dt)*randn(step)

# for i in 2:step
#     W[i] = W[i-1] + dW[i]
# end

# println("T = $T")
# println("W = $W")

T = [0.0, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09]
W = [0.0, 0.058763734934133255, -0.3064429609662668, -0.1150187791553188, 0.20713134172141554, 0.118633670957381, 0.39487790707242687, 0.1440882274695458, -0.007232462279190721, -0.16312644695165768]

plot(xlims=(-dt,maximum(T)), ylims=(minimum(W)-0.15, maximum(W)), fmt=:png)

for i in 1:step
    plot!([T[i],T[i]], [W[i],minimum(W)-0.125], label="", ls=:dash, lc="#000000", alpha=0.5)
end

for i in 1:step-1
    plot!([T[i],T[i]], [W[i],W[i+1]], label="", lc="#24292E", arrow=(:closed, 2.0))
    plot!([T[i],T[i+1]], [minimum(W)-0.05,minimum(W)-0.05], label="", lc="#24292E", arrow=(:closed, 2.0))
    plot!([T[i],T[i+1]], [W[i+1],W[i+1]], label="", ls=:dash, lc="#000000", alpha=0.5)
    plot!(annotations=((T[i]+T[i+1])/2, minimum(W)-0.09, ("\$+\\Delta t\$", 7, 0.0, :center)))
    if !(i in [3,7])
        plot!(annotations=(T[i]-dt/2, (W[i]+W[i+1])/2, ("\$+\\Delta W_$i\$", 7, 0.0, :center)))
    end
end

i = 3
plot!(annotations=(T[i], W[i+1]+0.02, ("\$+\\Delta W_$i\$", 7, 0.0, :bottom)))
i = 7
plot!(annotations=(T[i]-dt/2, W[i+1], ("\$+\\Delta W_$i\$", 7, 0.0, :center)))

plot!(T, W, xlabel="\$i\\Delta t\$", ylabel="\$W_i\$", label="", lc=1, lw=2)

savefig("wiener_process_description.png")
plot!()

白色雑音を取り巻く問題

厳密には, 白色雑音 $R(t)$ は確率超過程というものに分類され, 連続確率過程(そもそも確率過程)ではない. 一方, Wiener過程 $W(t)$ は連続確率過程の例である.

白色雑音 $R(t)$ はWiener過程 $W(t)$ の形式的な微分に相当する確率過程であるから, ちょうど双六でいうところのサイコロの目 $R_i$ と進んだマスの数 $X_i$ や, ランダムウォークモデルで言うところのコインの裏表 $R_i$ と進んだマスの数 $X_i$ と似たような関係である. ただし, 以下の点に注意しよう.

結論から言うと, このような白色雑音は, 数学的には確率過程のカテゴリーに入れて議論することができない

―　兼清泰明『確率微分方程式とその応用』(森北出版, 2017) p.100

白色雑音を数学的に厳密に取り扱うには, 確率超過程と呼ばれる概念を導入しなければならない

―　兼清泰明『確率微分方程式とその応用』(森北出版, 2017) p.100

白色雑音を数学的な議論の出発点とするのは適切ではない.

―　堀淳一『ランジュバン方程式』(岩波書店, 2015) p.53

2乗平均微分可能性の判定定理によって, $W(t)$ は2乗平均微分可能でなく, $W(t)$ の微分過程として白色雑音 $P(t)$ を定義することはできない

―　堀淳一『ランジュバン方程式』(岩波書店, 2015) p.54

連続時間過程としての白色雑音は厳密には存在しないため, もちろんそのグラフを正確に図示することはできない.

―　兼清泰明『確率微分方程式とその応用』(森北出版, 2017) p.102

確率微分方程式

微分方程式の解は微分可能でなければならない. Brown運動の軌道は明らかに微分可能ではないから, Brown運動の運動方程式(微分方程式)を考えるのはおかしい. そのようなわけで, Langevin方程式は通常の微分方程式としては解釈できない. ではどのように解釈すればよいかというと, 確率積分を含む方程式の別表記と考えるのである. というわけで, SDEは微分方程式というよりはむしろ積分方程式である. 確率微分方程式には確率積分としてIto積分を採用する立場とStratonovich積分を採用する立場の2つの立場があるが, このノートでは全てIto積分を採用する.

(3.2.3)の第2の積分をIto積分と解釈したとき, これらの方程式をItoのLangevin方程式あるいはItoの方程式という.
　―　堀淳一『ランジュバン方程式』(岩波書店, 2015) p.61

\begin{aligned} \frac{{\rm d}X(t)}{{\rm d}t} = f(X(t),t) + g(X(t),t)R(t) &&(3.2.1)\\ \mathrm{d}X(t) = f(X(t),t)\mathrm{d}t + g(X(t),t)\mathrm{d}W(t) &&(3.2.2)\\ X(t)-X(t_0) = \int_{t_0}^{t_1} f(X(s),s){\rm d}s + \int_{t_0}^{t_1} g(X(s),s){\rm d}W(s) &&(3.2.3) \end{aligned} (3.2.3)

Ito方程式(3.2.1)～(3.2.3)をBrown運動の運動方程式(Langevin方程式)として解釈しようとすると, $X(t)$ は速度だと思わなくてはいけないので $V(t)$ の記号に変えた方がよい. また, $f(X(t),t)=-\gamma X(t), g(X(t),t)=1$ の時が狭義でのLangevin方程式なので, かなり一般化されている. そのため, 「一般化Langevin方程式」とでも呼びたいところだが, これはまた別の方程式を指す名称なので紛らわしい. (3.2.1)～(3.2.3)をItoのLangevin方程式と呼ぶのは誤解を招くであろうから, このノートでは単にIto方程式と呼ぶ.

Fokker-Planck方程式

確率論と解析学の間には実り多い相互関係がある. その研究は少なくともKolmogorov(1931)にさかのぼる. (中略) 楕円型, 放物型偏微分方程式の多くの問題の解は確率汎関数の期待値として表現することができる.
― L.カラザス, S.E.シュレーブ著, 渡邉壽夫訳『ブラウン運動と確率積分』(丸善出版, 2012) 第4章 4.1序論

このノートでは, 上記のEular-Maruyama法による数値解の妥当性をFokker-Planck方程式によって評価する. Ito方程式

\frac{{\rm d}X(t)}{{\rm d}t} = f(X(t),t) + g(X(t),t)R(t)

の解 $X(t)$ の確率密度関数 $P(x,t)$ が従う偏微分方程式としてFokker-Planck方程式

\frac{\partial P(x,t)}{\partial t} = \frac{\partial^2 [D_u (g(x,t))^2 P(x,t)]}{\partial x^2}-\frac{\partial [f(x,t)P(x,t)]}{\partial x}

が知られている. 以下に具体例をまとめる. 今回は $D=D_u$ としてよい.

条件	Ito方程式	Fokker-Planck方程式
$f(X(t),t)=0, g(X(t),t)=1$	${\frac{{\rm d}X(t)}{{\rm d}t}=R(t)}$ Wiener過程	$\frac{\partial P(x,t)}{\partial t}=D\frac{\partial^2 P(x,t)}{\partial x^2}$ 拡散方程式
$f(X(t),t)=c, g(X(t),t)=1$	${\frac{{\rm d}X(t)}{{\rm d}t}=c + R(t)}$ ドリフト項のあるWiener過程	$\frac{\partial P(x,t)}{\partial t}=D\frac{\partial^2 P(x,t)}{\partial x^2}-c\frac{\partial P(x,t)}{\partial x}$ 移流拡散方程式
$f(X(t),t)=-\gamma X(t), g(X(t),t)=1$	${\frac{{\rm d}X(t)}{{\rm d}t}=-\gamma X(t) + R(t)}$ Ornstein–Uhlenbeck過程	$\frac{\partial P(x,t)}{\partial t}=D\frac{\partial^2 P(x,t)}{\partial x^2}-\frac{\partial (-\gamma XP(x,t))}{\partial x}$ 名前なし

初期条件 $P(x,0) = \delta(x-x_0)$ , 境界条件 $P(\pm\infty,t)=0$ のときの解はそれぞれ以下の通りである.

\begin{aligned} P(x,t) = \frac{1}{\sqrt{4\pi Dt}} \exp \left( -\frac{(x-x_0)^2}{4Dt} \right) \\ P(x,t) = \frac{1}{\sqrt{4\pi Dt}} \exp \left( -\frac{(x-x_0-ct)^2}{4Dt} \right) \\ P(x,t) = \sqrt{\frac{\gamma}{2\pi D(1-e^{-2\gamma t})}} \exp \left( -\frac{\gamma(x-x_0 e^{-\gamma t})^2}{2D(1-e^{-2\gamma t})} \right) \end{aligned}

揺動力の強さ $D_u$ と拡散係数 $D$

後に説明するが, 拡散方程式( $f(X(t),t)=0, g(X(t),t)=1$ のIto方程式)とLangevin方程式の導く平均二乗変位 $\langle|X(t)|^2\rangle$ は異なるものである. 拡散係数を求める際によく目にする $\langle|X(t)|^2\rangle = 2nDt$ とLangevin方程式から導かれる $\langle|\boldsymbol{X}(t)|^2\rangle = 2n\frac{D_u m}{\gamma^3} \left(\frac{\gamma}{m} t+e^{-\frac{\gamma}{m} t}-1 \right)$ は, 特定の条件下でのみEinsteinの関係式

D = \frac{D_u}{\gamma^2} = \frac{k_\mathrm{B}T}{\gamma}

で結ばれる. Fokker-Planck方程式の説明だけを見ると揺動力の強さ $D_u$ と拡散係数 $D$ は一致するように見えるが, Langrvin方程式を見据えると, 揺動力の強さ $D_u$ と拡散係数 $D$ は明確に区別することが教育的であると思われる.

数値計算

ここではEular-Maruyama法を用いてWiener過程, ドリフト項のあるWiener過程, Ornstein–Uhlenbeck過程を数値的に解く.

Eular-Maruyama法

Eular-Maruyama法は確率初期値問題

\frac{{\rm d}X(t)}{{\rm d}t} = f(X(t),t) + g(X(t),t)R(t),\\ t\in[t_0,T], X(t_0)=X_0

を次のように離散化する方法である.

X_{i+1} \simeq X_i + f(X_i, t)\Delta t + g(X_i, t)\Delta W_i

このとき, $\Delta t$ は時間刻み幅で, 粗い計算なら0.1などを選ぶ. $\Delta W_i$ は正規分布 $N(0,2D_u\Delta t)$ に従う疑似乱数である. Eular-Maruyama法はEular法の一般化であり, $g(X(t),t)=0$ の場合はEular法と一致する. 詳細な説明および高次の方法については三井(2004), 兼清(2017), Ogawa(2001), またはこちらの記事を参照されたい.

Wiener過程

Wiener過程がGauss分布 $N(0,t)$ に従うことは定義に含まれているのだが, Ito方程式の特殊化としてWiener過程を考えることで, Fokker-Planck方程式の議論から拡散方程式との関係を理解できる.
Wiener過程はIto方程式の $f(X(t),t)=0, g(X(t),t)=1$ の場合である.

\frac{{\rm d}X(t)}{{\rm d}t} = R(t)\\ {\rm d}X(t) = {\rm d}W(t)\\ X(t)-X(t_0) = \int_{t_0}^{t_1} {\rm d}W(s)

Eular-Maruyama法による離散化は次式である.

X_{i+1} \simeq X_i + \Delta W_i

対応するFokker-Planck方程式は次式である. これは拡散方程式と呼ばれる.

\frac{\partial P(x,t)}{\partial t}=D\frac{\partial^2 P(x,t)}{\partial x^2}

対応する初期条件はそれぞれ

X(0) = X_0\\ P(x,0) = \delta(x-x_0)

であり, 境界条件 $P(\pm\infty,t)=0$ のときの解は次式である.

P(x,t) = \frac{1}{\sqrt{4\pi Dt}} \exp \left( -\frac{(x-x_0)^2}{4Dt} \right)

function SDE()    
    # パラメータ：
    N = 5000        # 粒子数
    dt = 0.1        # 時間刻み幅
    step = 50       # 時間ステップ
    name = "SDE_1"  # ファイル名
    x0 = 0          # 初期位置
    Du = 1.5        # 揺動力の強さ(一般には拡散係数Dと一致しない)
    D  = Du         # 厳密解の計算で使う拡散係数D
    f(x,t) = 0      # 外力のようなもの
    g(x,t) = 1      # 今回は1
    exact(x) = exp(-(x-x0)^2/(4*D*t)) / sqrt(4*D*pi*t)

    # 初期値：
    t = 0.0
    X = fill(x0, N)
    Y = [-0.01-0.1*i/N for i in 1:N] # 描写のときのサンプルのy座標. 計算には関係ない
    anim = Animation()

    for i in 1:step
        # 描写：
        plt = scatter(X, Y, xlims=(-5,5), ms=1, msw=0, mc="#3261AB", label="Sample", xlabel="\$x\$", ylabel="\$P(x,t)\$")
        histogram!(plt, X, bins=range(-5,5,step=0.2), ylims=(-0.14,1.0), normed=true, label="Histogram", fa=0.3, fc=1, lc="#FFFFFF")
        plot!(plt, exact, lw=2, lc="#393e46", label="Exact PDF", title= @sprintf("t = %.2f",t))
        frame(anim,plt)
        # 計算：
        t += dt
        X += f.(X,t)*dt + g.(X,t).*sqrt(2*Du*dt).*randn(N)
    end

    gif(anim, name*".gif", fps=15)
end

SDE()

ドリフト項のあるWiener過程

Ito方程式の $f(X(t),t)=c, g(X(t),t)=1$ の場合としてドリフト項のあるWiener過程を考える.

\frac{{\rm d}X(t)}{{\rm d}t} = c + R(t)\\ {\rm d}X(t) = c{\rm d}t + {\rm d}W(t)\\ X(t)-X(t_0) = \int_{t_0}^{t_1} c{\rm d}s + \int_{t_0}^{t_1} {\rm d}W(s)

Eular-Maruyama法による離散化は次式である.

X_{i+1} \simeq X_i + c\Delta t + \Delta W_i

対応するFokker-Planck方程式は次式である. これは移流拡散方程式と呼ばれる.

\frac{\partial P(x,t)}{\partial t} = D\frac{\partial^2 P(x,t)}{\partial x^2} - c \frac{\partial P(x,t)}{\partial x}

対応する初期条件はそれぞれ

X(0) = X_0\\ P(x,0) = \delta(x-x_0)

であり, 境界条件 $P(\pm\infty,t)=0$ のときの解は次式である.

P(x,t) = \frac{1}{\sqrt{4\pi Dt}} \exp \left( -\frac{(x-x_0-ct)^2}{4Dt} \right)

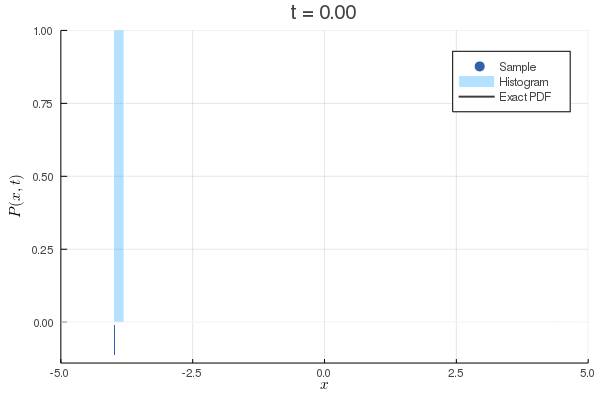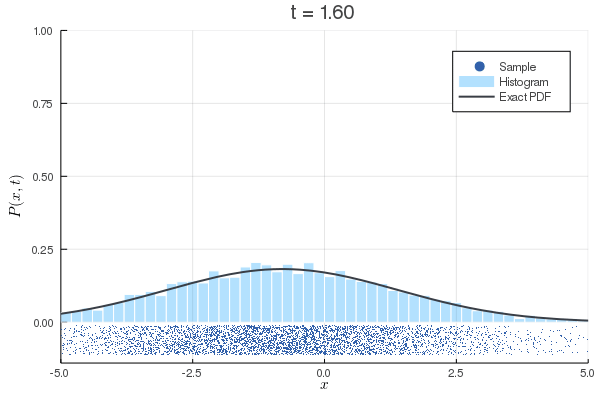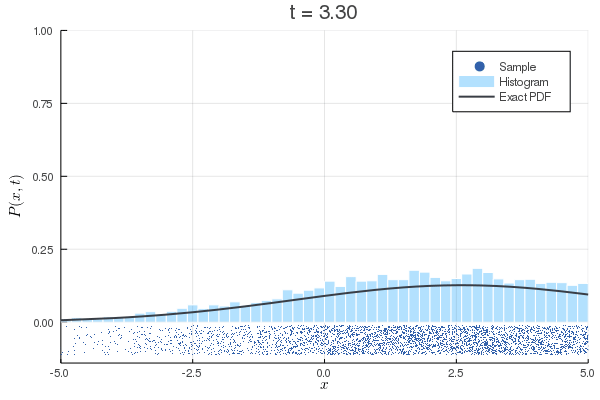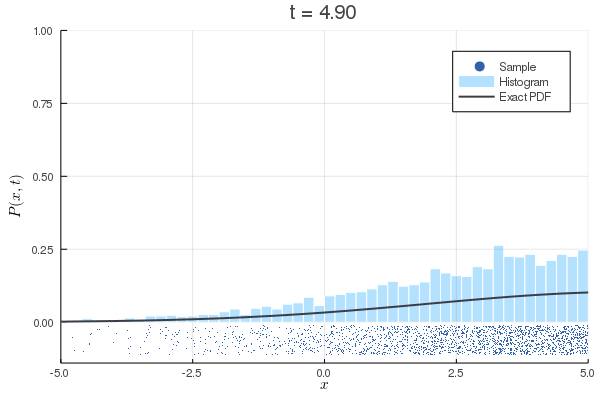
上記の解は全領域 $-\infty<x<\infty$ で規格化されており, Plots.jlのヒストグラムは描写領域内(下図だと $-5<x<5$ )で規格化されているため, 描写領域からはみ出す粒子が多くなるとズレる.

function SDE()    
    # パラメータ：
    N = 5000        # 粒子数
    dt = 0.1        # 時間刻み幅
    step = 50       # 時間ステップ
    name = "SDE_2"  # ファイル名
    x0 = -4         # 初期位置
    Du = 1.5        # 揺動力の強さ(一般には拡散係数Dと一致しない)
    D = Du          # 厳密解の計算で使う拡散係数D
    c = 2.0         # 移流係数
    f(x,t) = c      # 外力のようなもの
    g(x,t) = 1      # 今回は1
    exact(x) = exp(-(x-x0-c*t)^2/(4*Du*t))/sqrt(4*pi*Du*t)

    # 初期値：
    t = 0.0
    X = fill(x0, N)
    Y = [-0.01-0.1*i/N for i in 1:N] # 描写のときのサンプルのy座標. 計算には関係ない
    anim = Animation()

    for i in 1:step
        # 描写：
        plt = scatter(X, Y, xlims=(-5,5), ms=1, msw=0, mc="#3261AB", label="Sample", xlabel="\$x\$", ylabel="\$P(x,t)\$")
        histogram!(plt, X, bins=range(-5,5,step=0.2), ylims=(-0.14,1.0), normed=true, label="Histogram", fa=0.3, fc=1, lc="#FFFFFF")
        plot!(plt, exact, lw=2, lc="#393e46", label="Exact PDF", title= @sprintf("t = %.2f",t))
        frame(anim,plt)
        # 計算：
        t += dt
        X += f.(X,t)*dt + g.(X,t).*sqrt(2*Du*dt).*randn(N)
    end

    gif(anim, name*".gif", fps=15)
end

SDE()

Ornstein–Uhlenbeck過程

$X(t)$ は変位ではなく速度として解釈するほうがよい. つまり, $\gamma$ は粘性抵抗である. Ornstein–Uhlenbeck過程はIto方程式の $f(X(t),t)=-\gamma X(t), g(X(t),t)=1$ の場合である.

\frac{{\rm d}X(t)}{{\rm d}t} = -\gamma X(t) + R(t)\\ {\rm d}X(t) = -\gamma X(t){\rm d}t + {\rm d}W(t)\\ X(t)-X(t_0) = \int_{t_0}^{t_1} -kX(s){\rm d}s + \int_{t_0}^{t_1} {\rm d}W(s)

Eular-Maruyama法による離散化は次式である.

X_{i+1} \simeq X_i + c\Delta t + \Delta W_i

対応するFokker-Planck方程式は次式である.

\frac{\partial P(x,t)}{\partial t} = D\frac{\partial^2 P(x,t)}{\partial x^2} - \frac{\partial (-\gamma XP(x,t))}{\partial x}

対応する初期条件はそれぞれ

X(0) = X_0\\ P(x,0) = \delta(x-x_0)

であり, 境界条件 $P(\pm\infty,t)=0$ のときの解は次式である. なお, $P(x,t)$ はWikipedia, 大平(2017) p.166, 堀(2015) p.に載っている.

P(x,t) = \sqrt{\frac{\gamma}{2\pi D(1-e^{-2\gamma t})}} \exp \left( -\frac{\gamma(x-x_0 e^{-\gamma t})^2}{2D(1-e^{-2\gamma t})} \right)

f(x)による横方向の移動はEular法で計算しており, 本来ならば短い時間刻みの間にも徐々に移動速度が小さくなっていくべきところを, 大きい速度のまま計算してしまっている. これはdtを小さくするか, 高次のスキームを使うなどすれば改善されるはずである.

function SDE()    
    # パラメータ：
    N = 5000        # 粒子数
    dt = 0.1        # 時間刻み幅
    step = 50       # 時間ステップ
    name = "SDE_3"  # ファイル名
    x0 = -4         # 初期位置
    Du = 1.5        # 揺動力の強さ(一般には拡散係数Dと一致しない)
    D  = Du         # 厳密解の計算で使う拡散係数D
    γ = 1.5        # 粘性抵抗のようなもの
    f(x,t) = -γ*x  # 外力(粘性抵抗)のようなもの
    g(x,t) = 1      # 今回は1
    exact(x) = exp(-γ*(x-x0*exp(-γ*t))^2/(2*D*(1-exp(-2*γ*t))))*sqrt(γ/(2*pi*D*(1-exp(-2*γ*t))))

    # 初期値：
    t = 0.0
    X = fill(x0, N)
    Y = [-0.01-0.1*i/N for i in 1:N] # 描写のときのサンプルのy座標. 計算には関係ない
    anim = Animation()

    for i in 1:step
        # 描写：
        plt = scatter(X, Y, xlims=(-5,5), ms=1, msw=0, mc="#3261AB", label="Sample", xlabel="\$x\$", ylabel="\$P(x,t)\$")
        histogram!(plt, X, bins=range(-5,5,step=0.2), ylims=(-0.14,1.0), normed=true, label="Histogram", fa=0.3, fc=1, lc="#FFFFFF")
        plot!(plt, exact, lw=2, lc="#393e46", label="Exact PDF", title= @sprintf("t = %.2f",t))
        frame(anim,plt)
        # 計算：
        t += dt
        X += f.(X,t)*dt + g.(X,t).*sqrt(2*Du*dt).*randn(N)
    end

    gif(anim, name*".gif", fps=15)
end

SDE()

付録

拡散方程式の導出

コインの試行と言えば二項分布だが, 試行回数が多い時は正規分布に近似できることが知られている. そのため, 連続極限 $\Delta t\rightarrow0$ というよりは, 試行回数が $\frac{t}{\Delta t} \rightarrow\infty$ となることで拡散方程式の振る舞いに近づくことが予想できる. 実際, 太田(2000) p.67 はランダムウォークモデルの連続極限として拡散方程式を導出しており, 北原和夫『岩波基礎物理シリーズ 8 非平衡系の統計力学』(岩波書店, 1997) p.185は長時間極限としてガウス分布を導いている. また, 堀(2015) p.4 は一般の場合を考えて移流拡散方程式を導出している. ここでは, 有限差分法とちょうど逆の手順を踏んで拡散方程式を導出する.

サイコロを振って, 表なら $+\Delta x$ , 裏なら $-\Delta x$ だけ進むものとする. また. 時刻を $t$ とし, 時間間隔 $\Delta t$ ごとにサイコロを振るものとする. 格子点 $x$ 上にいる確率 $P(x,t+\Delta t)$ は, 半分が左から, 半分が右からやってくるので

P(x,t+\Delta t) = \frac{1}{2} P(x+\Delta x, t) + \frac{1}{2} P(x-\Delta x,t)

である. 両辺から $P(x,t)$ を引くと,

\begin{aligned} P(x,t+\Delta t) - P(x,t) &= \frac{1}{2} P(x+\Delta x,t) - P(x,t) + \frac{1}{2} P(x-\Delta x,t) \\ &= \frac{1}{2} \bigg[ P(x+\Delta x,t) - 2P(x,t) + P(x-\Delta x,t) \bigg] \\ &= \frac{1}{2} \bigg[ \big[ P(x+\Delta x,t) - P(x,t) \big] - \big[ P(x,t) - P(x-\Delta x,t) \big] \bigg] \\ \end{aligned}

のように変形できる. 最後に両辺を $\Delta t =: a\Delta x^2$ で割ってから $\Delta t, \Delta x\rightarrow0$ を考えると.

\begin{aligned} P(x,t+\Delta t) - P(x,t) &= \frac{1}{2} \bigg[ \big[ P(x+\Delta x,t) - P(x,t) \big] - \big[ P(x,t) - P(x-\Delta x,t) \big] \bigg] \\ \frac{P(x,t+\Delta t) - P(x,t)}{\Delta t} &= \frac{1}{2a} \frac{1}{\Delta x} \bigg[ \frac{P(x+\Delta x,t)-P(x,t)}{\Delta x} - \frac{P(x,t) - P(x-\Delta x,t)}{\Delta x} \bigg] \\ \frac{\partial P(x,t)}{\partial t} &= \frac{1}{2a} \frac{1}{\Delta x} \bigg[ \frac{\partial P(x,t)}{\partial x} - \frac{\partial P(x-\Delta x,t)}{\partial x} \bigg] \\ \frac{\partial P(x,t)}{\partial t} &= \frac{1}{2a} \frac{\partial^2 P(x,t)}{\partial x^2} \end{aligned}

となり, $D=\frac{1}{2a}$ とした拡散方程式を得る. なお, 以上は解析的な結果であって, 拡散方程式の解は $|x|<\pm\infty$ まで値を取りうるが, ランダムウォークの場合は $|x|<\pm i\Delta x$ までしか取り得ないという点において, 数値的に完全に一致する結果は得られない.

数値的に再現するには, ヒストグラムの面積に気を遣わなければいけない. ランダムウォークは偶数か奇数の格子上にしか分布しない(例えば２回コインを投げると-2, 0, 2であり, -1や1には存在しない)ので. step=dxとすると, ヒストグラムの総面積を1にする都合上, 高さが2倍になってしまう. そのため, 隙間ができないようにstep=2*dxとしなければならない. さらに, 浮動小数点の都合上, 格子点上からは若干ズレるので, ヒストグラムの端は格子点上よりも格子の間においた方がよい.

function RW2D(N, step)
    X = zeros(N)
    
    for i in 1:step
        X += (floor.(rand(N)*2) .- 0.5)*2
    end

    exact(D,x,t) = exp(-x^2/(4*D*t)) / sqrt(4*D*pi*t)
    D = 2.0
    dx = 0.1
    dt = dx^2/(2*D)

    return plot!(
        histogram(X*dx, bins=range(minimum(X*dx)-dx/2,maximum(X*dx)+dx/2,step=dx*2), normed=true, label="", title="N=$N,step=$step", titlefontsize=10, fa=0.3, fc=1, lc="#FFFFFF"),
        x->exact(D,x,step*dt), label="", lw=2, lc="#393e46"
    )
end

plt = []
for j in [5,20,100]
    for i in [10,100,10000]
        push!(plt, RW2D(i,j))
    end
end
plot(plt...)

参考文献

太田隆夫『非平衡系の物理学』(裳華房, 2000) p.67
ランダムウォークモデルの連続極限として拡散方程式を導出している. 拡散方程式を経由して, Wiener過程とランダムウォークの対応関係を考えるときに参考になる.
石村直之『確率微分方程式入門―数理ファイナンスへの応用― 』(共立出版, 2014) pp.6,74,75
確率過程や確率微分方程式の定義を参考にした.
大平徹『確率論講義ノート場合の数から確率微分方程式まで』(森北出版, 2017) pp.118,160,165,166,167
確率過程の定義を参考にした. Ornstein–Uhlenbeck過程の解が載っている.
兼清泰明『確率微分方程式とその応用』(森北出版, 2017) p.1,100,102
白色雑音を取り巻く数学的な困難さについて述べられている. Ito-Taylor展開を用いた近似スキームの導出はこちらを参考にされたい.
B.エクセンダール著, 谷口説男訳『確率微分方程式入門から応用まで』(丸善出版, 2012)
L.カラザス, S.E.シュレーブ著, 渡邉壽夫訳『ブラウン運動と確率積分』(丸善出版, 2012)
堀淳一『ランジュバン方程式』(岩波書店, 2015) pp.4, 53, 54, 61, 80
数学的にも厳密であり, かつ物理への応用例が非常に充実している. 白色雑音についての困難さについても述べられており, Ito積分やItoのLangevin方程式についての説明がある. Ito方程式の定義はこれを参考にした.
三井斌友, 小藤俊幸, 斉藤善弘『微分方程式による計算科学入門』(共立出版, 2004) pp.139, 150
SDEの数値計算について解説している希少な和書である. Eular-Maruyama法の表記はこれを参考にした.

この記事は2021年10月23日(土)に行われた第8回ぶつりがく徒のつどいの講演資料を元に改良を加えたものです. 記事の元になったノートはGistにアップロードしてあります.

パッケージ

確率過程

ランダムウォークモデル

白色雑音とWiener過程

白色雑音を取り巻く問題

確率微分方程式

Fokker-Planck方程式

揺動力の強さD_uと拡散係数D

数値計算

Eular-Maruyama法

Wiener過程

ドリフト項のあるWiener過程

Ornstein–Uhlenbeck過程

付録

拡散方程式の導出

参考文献

Discussion

揺動力の強さ $D_u$ と拡散係数 $D$