⛰️

ガウス型軌道の形と軌道指数の関係

2023/12/14に公開

Julia

物理

化学

tech

量子化学で用いられる1sガウス型軌道の形と軌道指数の関係を可視化します. A.ザボ, N.S.オストランド著, 大野公男, 阪井健男, 望月祐志訳『新しい量子化学上　電子構造の理論入門』(東京大学出版会, 1987)の第3章より

\phi_\mathrm{1s}^{\mathrm{GF}}\left(\alpha, \boldsymbol{r}-\boldsymbol{R}_A\right) = \left(\frac{2 \alpha}{\pi}\right)^{3 / 4} \mathrm{e}^{-\alpha\left|\boldsymbol{r}-\boldsymbol{R}_A\right|^2} \tag{3.203}

の $\alpha$ を変えていきましょう. 原点を中心として次のように関数を実装できます.

φ(r;α=1.0) = (2*α/π)^(3/4) * exp(-α*r^2)

数値積分で規格化条件 $\int 4\pi r^2 |\phi(r)|^2 \mathrm{d}r=1$ を確認しておきましょう. 積分にはQuadGK.jlを用います. using Pkg; Pkg.add("QuadGK") でインストールした後に, 次のように積分を計算できます.

入力

using QuadGK
println("α = 1.0,\t∫4πr²|φ(r)|²dr = ", quadgk(r -> 4π*r^2*φ(r;α=1.0)^2, 0, Inf)[1])
println("α = 2.0,\t∫4πr²|φ(r)|²dr = ", quadgk(r -> 4π*r^2*φ(r;α=2.0)^2, 0, Inf)[1])
println("α = 3.0,\t∫4πr²|φ(r)|²dr = ", quadgk(r -> 4π*r^2*φ(r;α=3.0)^2, 0, Inf)[1])
println("α = 10.0,\t∫4πr²|φ(r)|²dr = ", quadgk(r -> 4π*r^2*φ(r;α=10.0)^2, 0, Inf)[1])

出力

α = 1.0,	∫4πr²|φ(r)|²dr = 1.0000000000000138
α = 2.0,	∫4πr²|φ(r)|²dr = 1.0000000000000002
α = 3.0,	∫4πr²|φ(r)|²dr = 0.9999999999999999
α = 10.0,	∫4πr²|φ(r)|²dr = 0.9999999999996987

正しく規格化されていますね. 次に, 可視化に使用するためPlots.jlをインストールしておきましょう. using Pkg; Pkg.add("Plots") でインストールできます. これを使って軌道を可視化できます.

入力

using Plots
plot(xlabel="\$r\$", ylabel="\$\\phi(r)\$", xlim=(0,3))
plot!(r -> φ(r,α=1.0), label="\$\\alpha=1.0\$")
plot!(r -> φ(r,α=2.0), label="\$\\alpha=2.0\$")
plot!(r -> φ(r,α=3.0), label="\$\\alpha=3.0\$")
plot!(r -> φ(r,α=10.0), label="\$\\alpha=10.0\$")

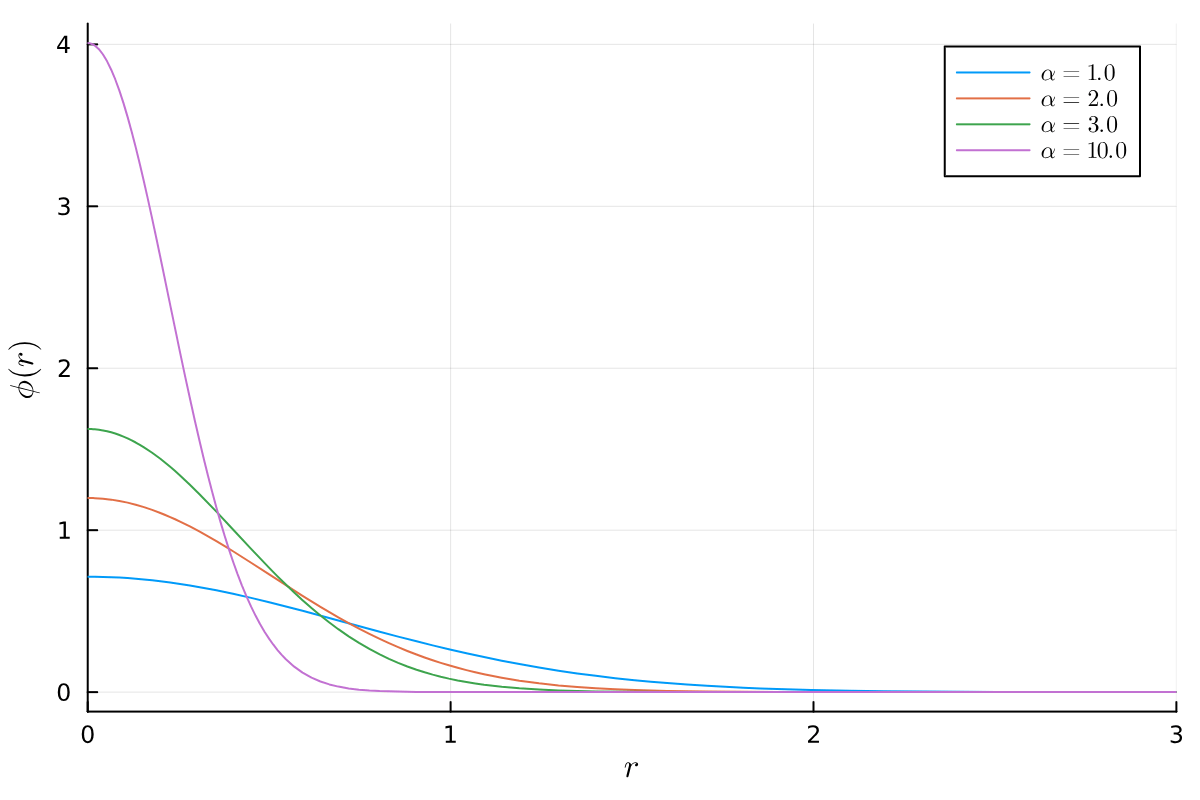
このように, 軌道指数 $\alpha$ が大きいほどガウス型軌道は縮んでいる. 逆に, 軌道指数が小さいほど軌道指数は拡がっていることが確認できました.

Discussion