Zenn
👁️

めぐろLTは本当に目黒なのか白黒つける

2023/12/21に公開
#
数理最適化
tech

はじめに

本記事はめぐろLT Advent Calendar 202319日目の記事になります。

めぐろLTは本当に目黒なのかを白黒つけます。
忙しい人はここから新しく提案した「めぐろ」の領域が見れるので試してみてください。

めぐろLTとは

めぐろLTは
「目黒100km圏内を対象に、主にWeb系のプロダクト開発事業をしている複数社共同でゆるめに開催しているLTコミュニティです。」(connpasより引用)
私自身は第二回の開催から、登壇・観戦者として何度か参加させていただきました。
雰囲気が非常に良く(語彙力)、登壇に対する心理的な安心感があることからも、学内の後輩たちにも勧めて定期的なアウトプットの場として活用させていただいています。
あとピザとかいっぱい食べれる。

この説明にある 「目黒100km圏内を対象」 をよく覚えておいてください。

めぐろLTは本当に目黒なのか

さて、本題です。
先述したように、めぐろLTの公式(?)としての見解では 「目黒100km圏内を対象」 として目黒とみなしているようです。
「目黒100km圏内」を「目黒から半径100km以内」と解釈するとして、どのあたりまでが対象になるのかがピンとこないので、地理情報を簡単に扱えるツールjSTAT MAPを用いて確認してみましょう。


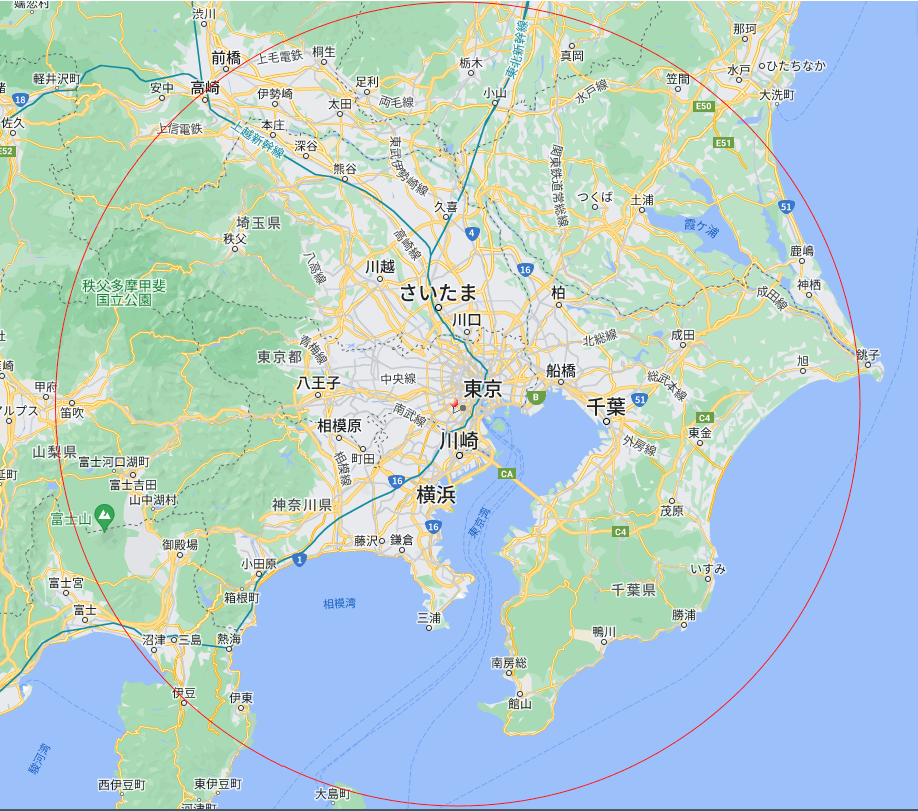
目黒区役所を中心に半径100kmの真円を描画した地図

図を見てもらえれば分かる様に、この定義だと富士山山頂でLT会を開催しても「めぐろLTである」と主張ができてしまうのです。
北の方面に目を向けてみると、「高崎はめぐろで前橋はめぐろではない」ということになってしまい前橋が可哀想です。いや、どっちも絶対めぐろじゃないと思うんですけどね。
これらのことから、「目黒100km圏内」をめぐろとすることには納得感というか説得力に欠けるのではないかと思います。

そこで、誰もが「それはめぐろだわ」と納得するような新たな定義を提案しようと思います。

要件定義

単純に半径を短くすれば良いのでは？と思うかもしれないので、試しに半径を10kmに変更した図を見てみましょう。


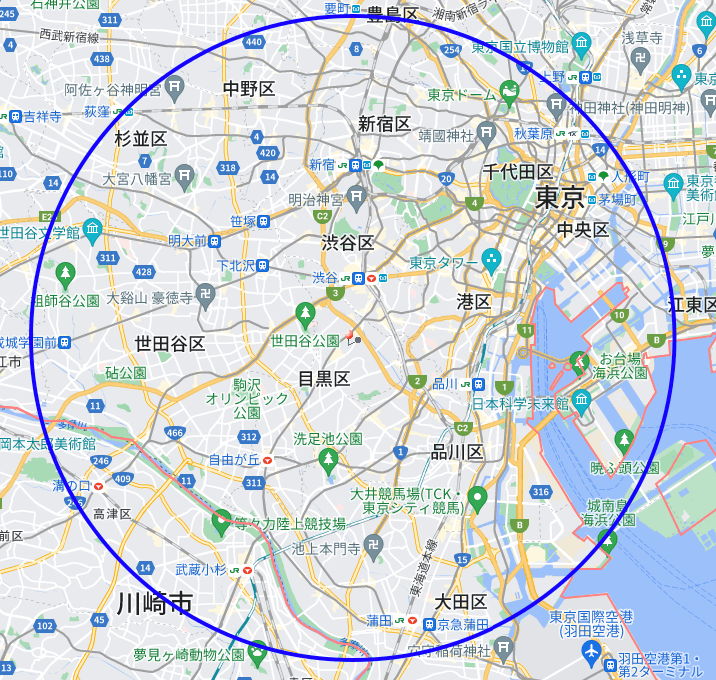
赤線は東京都と神奈川県の境目

だいぶ良くなった気はしますし、何ならこれで良いかもという気持ちもありますが、個人的には目黒区本来の形(領域)が全く考慮されていない点が気になります。
これは目黒区自体が非常に歪な形をしており、凹んでいる部分も出っ張っている部分も等しく円で判定されるのは凹んでいる側が損(?)するなぁという気持ちからきています。

というわけで、今回は目黒区の形を考慮しながら「めぐろ」を定義していきたいと思います。

その上で今回「めぐろ」を定義するにあたっての要件(守りたいこと)は以下の様になります。
上から順番に考える優先度を高くしています。

(1)目黒区の形を考慮する
→ より「めぐろ」っぽさを反映させるため

(2)「めぐろ」の範囲を可能な限り東京都内に収める
→ 東京以外を「めぐろ」とする違和感があるため
→ 一方で川崎市の一部等、目黒区と非常に近い神奈川県の市町村区が入っていても違和感はないので「可能な限り考慮」する

(3)できるだけ「めぐろ」の範囲を広くする
→ 範囲が広い方がみんな幸せ

これらの要件から 「東京都の中で目黒区を可能な限り大きくする」 計算をすることで目的が達成できると考えます。

手法

要件定義の(1)(2)を満たすために、東京都と目黒区の地形を利用するのですが、そのままの地形では複雑なので、諸々の計算が非常に面倒になります。
そこで、今回は東京都と目黒区の元の形から凸包を取り、その凸包を「東京都」「目黒区」として扱い計算をしていきます。

このことから、今回やりたい「東京都の中で目黒区を可能な限り大きくする」という計算は 「多角形の内側にある多角形を可能な限り面積を大きくする」 という計算に言い換えることができます。
そしてこれは何やかんやすると線形計画法という数理最適化の手法を用いて解くことができます。

計算方法

それなりにややこしいことをするので、数学っぽいことが好きじゃない！って人はすっ飛ばしてください。

アフィン変換

今我々が欲しいのは「元の形を変えずにサイズをなるべく大きくした多角形」です。
内側にある元の多角形(目黒区の凸包)にOという名前を、その多角形を最大限多くしたときの多角形にQという名前を付け、その多角形同士の対応する頂点に注目すると以下のようになります。


2つの多角形の関係性

多角形Qは最適化後の図形なので、この図でいうS,dx,dyの値をどうにか求めれば良いわけです。
このように平面を拡大・縮小したり平行移動させたりする計算はアフィン変換を利用します。
先程の平面の変換をアフィン変換を用いた式で表すと以下のようになります。
このとき、x^o_i,y^o_i,x^q_i,y^q_iは、平面O,Qの任意の頂点のx,y座標を表します。

\begin{pmatrix} x^o_i \\ y^o_i \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & d_x \\ 0 & 1 & d_y \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} S & 0 & 0 \\ 0 & S & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x^q_i \\ y^q_i \\ 1 \\ \end{pmatrix}

この式をせっせこ解いていくと任意の点と平行移動させる数値d_x,d_yについての式を以下のように得ることができます。
例としてx^o_iとd_xについて示します。
y座標について求めたければxの部分をyに変えるだけでOKです。

\begin{align*} x^o_i = Sx^q_i + d_x \end{align*} \\ \begin{align*} d_x = x^o_1 - Sx^q_1 \end{align*}

また、このとき縮小の倍率Sはその定義から以下のようになります。

\begin{align*} S = \frac {x^o_2 - x^o_1}{x^q_2 - x^q_1} \end{align*}

線形計画法

線形計画法が何かは、もっと詳しく解説してくれている記事がたくさんあるので興味があれば調べてみてください。
「特定の制限の元で関数の値が最も大きく(小さく)なるような変数の値を求める計算」だと思ってくれれば大丈夫です。
ここまでの話で得られた式から
外側の多角形の頂点：(x^p_1,y^p_1), \dots ,(x^p_n,y^p_n)
内側の多角形の頂点：(x^q_1,y^q_1), \dots ,(x^q_m,y^q_m)
とすると、以下のような線形計画問題に落とし込むことができます。

\begin{equation*} \begin{aligned} & [P_L]: \\ & \text{max} && \sum_j x^p_j \lambda _{2j} - \sum_j x^p_j \lambda _{1j} \\ & \text{subject to} && (x^o_2 - x^o_1) \sum_{j} \lambda _{ij}x^p_j - (x^o_2 - x^o_i) \sum_{j} \lambda _{ij}x^p_j + (x^o_1 - x^o_i) \sum_{j} \lambda _{2j}x^p_j = 0 \\ & && (x^o_2 - x^o_1) \sum_{j} \lambda _{ij}y^p_j - (x^o_2 - x^o_i) \sum_{j} \lambda _{ij}y^p_j + (y^o_1 - y^o_i) \sum_{j} \lambda _{2j}x^p_j + (y^o_i - y^o_1) \sum_{j} \lambda _{1j}x^p_1= 0 \\ & && \sum_j \lambda _{ij} = 1 \\ & && \lambda_{ij} \in \{0,1\} \\ & && 1 \leqq i \leqq n \\ & && 1 \leqq j \leqq m \\ \end{aligned} \end{equation*}

実際にやってみる

下準備

さて、こういった理屈で「めぐろ」を決めることができそうな目処が立ったところで、実際に計算をしていきます。
地理データは国土交通省が公開している国土数値情報ダウンロードサイトから東京都の情報のみをダウンロードして使用しています。

凸包を作成する前に、東京都内でも明らかに「めぐろ」ではないだろうという箇所を削りたいと思います。
今回は森林面積・人口らの要素を参考に、めぐろとは似ても似つかないと判断したものを対象外にします。
参考にした数値は全て各自治体が公表しているものを用いました。
以下は対象外にした地域とその理由です。

  • 山が存在するor森林面積が自治体面積の4割以上を占めている(めぐろには山がなく緑被率が20%)
    奥多摩町,檜原村,青梅市,あきる野市,八王子市

  • 都内の自治体別人口ランキングが千代田区未満
    日の出町,羽村市,福生市,瑞穂町

これに併せて、島嶼部は海上であるため対象外とし、町田市は神奈川県であるため当然対象外になります。
こうして新たに得られた「めぐろ」の範囲になり得る「ネオ東京」がこちらになります。


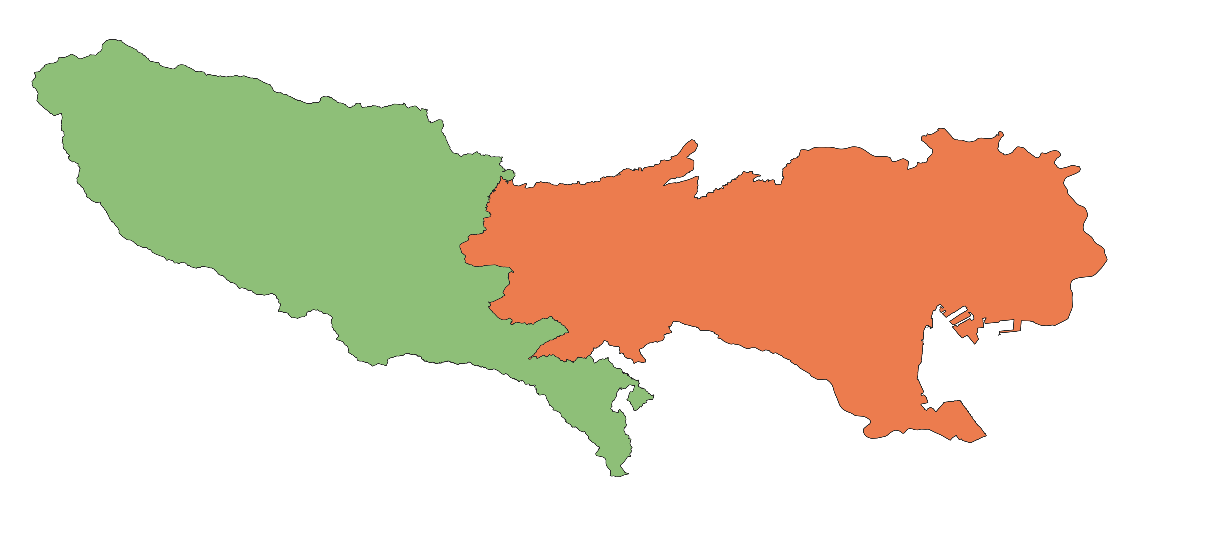
オレンジ色の部分が「ネオ東京」

凸包の作成

まずはネオ東京と目黒区の凸包を作成します。
地理情報から凸包を取るのは、地球が球面なこともあり座標変換等含めて全て自前でやるのは面倒なので、今回はQJISという便利なソフトウェアを使用して処理します。

実際にネオ東京と目黒区の地形とその凸包を取ったものをそれぞれ同時に描画してみるとこんな感じになります。


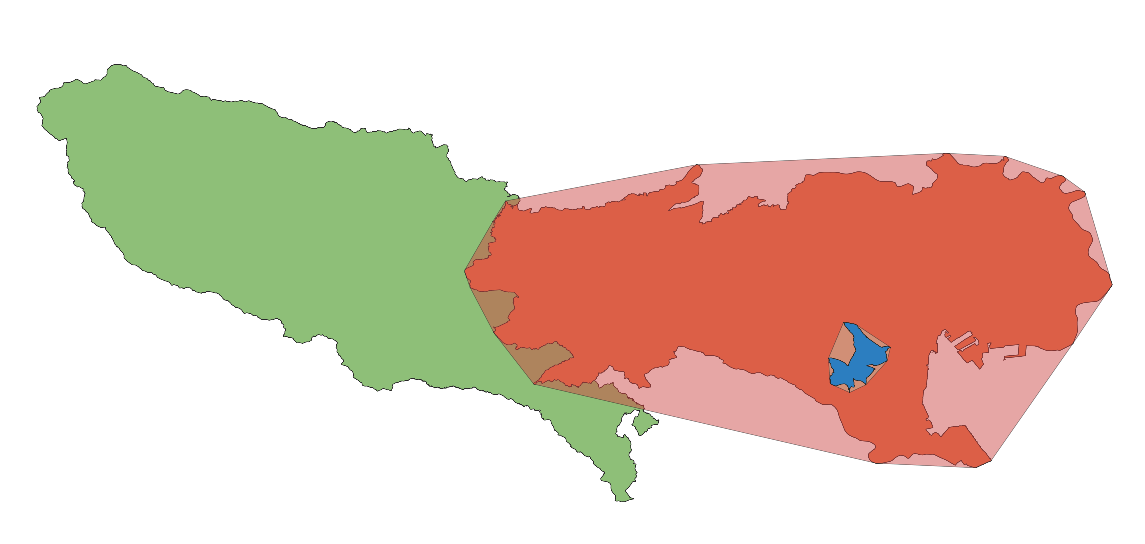
ネオ東京と目黒区とそれらの凸包


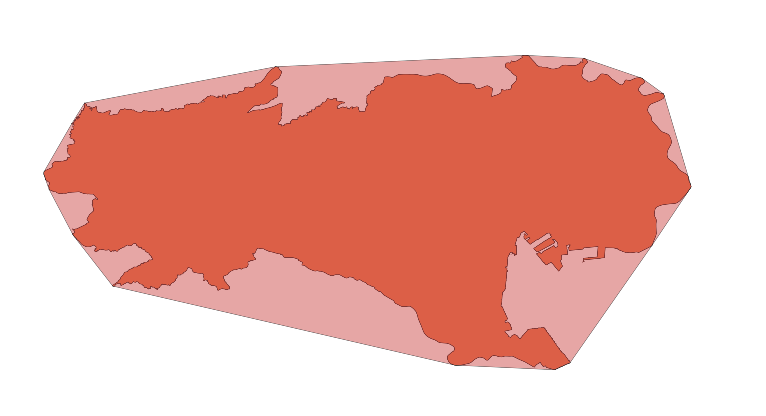
ネオ東京とその凸包


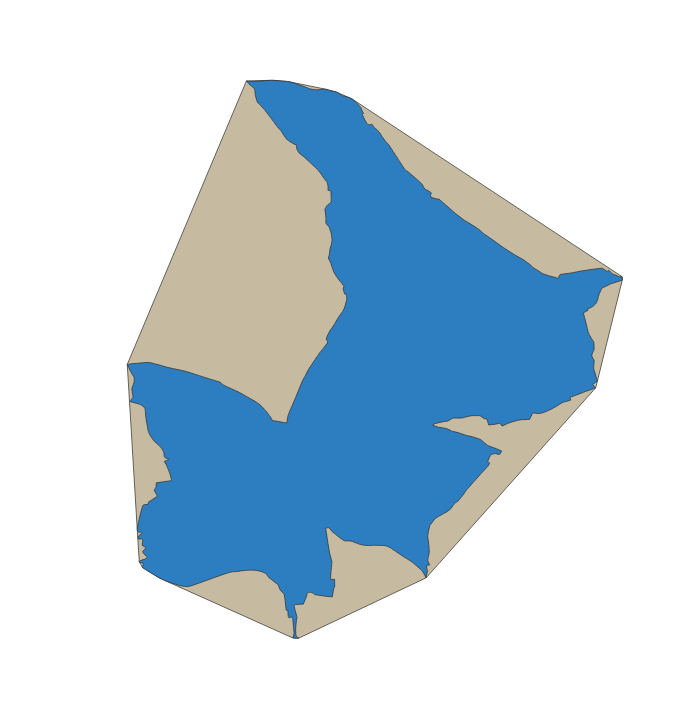
目黒区とその凸包

イメージをしてもらいやすくこのように図を並べましたが、実際に解いていく問題としては以下のような配置にある2つの多角形のうち、内側にある多角形の面積を可能な限り大きくすることになります。


2つの凸包だけを描画した様子

線形計画問題の解を求める

ここではpythonを用いてここまでの処理で得られた問題について解いていきます。
線形計画問題の計算には、条件を設定すると解を求めてくれる「ソルバー」というツールを用いることが多いのですが、今回はそのソルバーの中でもpulpというものを使用しました。

以下のような関数を作成し、引数に外側と内側の多角形のx,y座標配列を渡すことで各値を計算します。

import pulp
import numpy as np
import math

def solve_lp(outside_x_points,outside_y_points,inside_x_points,inside_y_points):
  problem = pulp.LpProblem('MaximizeMeguro', pulp.LpMaximize)

  out_sides = len(outside_x_points)
  in_sides = len(inside_x_points)

  #lambdaの初期化
  ones_array = np.ones(out_sides, dtype=int)
  lambda_dict = {}
  for i in range(in_sides):
    lambda_name = f'lambda{i+1}'
    lambda_i = [ pulp.LpVariable( lambda_name+'_{}'.format( i+1 ), lowBound=0, upBound=1, cat=pulp.LpContinuous ) for i in range(out_sides) ]
    lambda_dict[lambda_name] = lambda_i

  #目的関数
  assert len(ones_array) == len(outside_x_points) == len(outside_y_points) == len(lambda_dict["lambda1"])
  problem += pulp.lpDot( outside_x_points, lambda_dict["lambda2"] ) - pulp.lpDot( outside_x_points, lambda_dict["lambda1"] )

  #制約
  for i in range(in_sides):
    lambda_name = f'lambda{i+1}'
    problem += pulp.lpDot( ones_array, lambda_dict[lambda_name] ) == 1

    problem += (inside_x_points[1]-inside_x_points[0])*pulp.lpDot( outside_x_points, lambda_dict[lambda_name] ) \
    - (inside_x_points[1] - inside_x_points[i])*pulp.lpDot( outside_x_points, lambda_dict["lambda1"] ) \
    + (inside_x_points[0] - inside_x_points[i])*pulp.lpDot( outside_x_points, lambda_dict["lambda2"] ) == 0

    problem += (inside_x_points[1]-inside_x_points[0])*pulp.lpDot( outside_y_points, lambda_dict[lambda_name] ) \
    - (inside_x_points[1] - inside_x_points[0])*pulp.lpDot( outside_y_points, lambda_dict["lambda1"] ) \
    + (inside_y_points[0] - inside_y_points[i])*pulp.lpDot( outside_x_points, lambda_dict["lambda2"] ) \
    + (inside_y_points[i] - inside_y_points[0])*pulp.lpDot( outside_x_points, lambda_dict["lambda1"] ) == 0

  #solve
  status = problem.solve(pulp.PULP_CBC_CMD( msg=1, threads=4, timeLimit=100 ))

  #計算
  optimal_polygon_points = [[0,0],[0,0]]
  for i in range(out_sides):
    optimal_polygon_points[0][0] += lambda_dict["lambda1"][i].value()*p_x[i]
    optimal_polygon_points[1][0] += lambda_dict["lambda2"][i].value()*p_x[i]
    optimal_polygon_points[0][1] += lambda_dict["lambda1"][i].value()*p_y[i]
    optimal_polygon_points[1][1] += lambda_dict["lambda2"][i].value()*p_y[i]

  scale_y = math.sqrt(math.pow(optimal_polygon_points[1][0]-optimal_polygon_points[0][0],2)+(math.pow(optimal_polygon_points[1][1]-optimal_polygon_points[0][1],2)))
  s = math.sqrt(math.pow(inside_x_points[1]-inside_x_points[0],2)+math.pow(inside_y_points[1]-inside_y_points[0],2)) / scale_y
  dx = inside_x_points[0] - s*optimal_polygon_points[0][0]
  dy = inside_y_points[0] - s*optimal_polygon_points[0][1]

  #結果の出力
  print("optimal value", problem.objective.value())
  print("倍率：", 1/s)
  print("dx：", -dx)
  print("dy：", -dy)

実際に実行をしてみると以下のような結果が得られました。

optimal value 0.005301691541113485
倍率： 4.442054953126147
dx： -108.22157051504509
dy： -27.601079802455317

ここで得れらた各値から面積を最大化した多角形を描画するとこんな感じに。


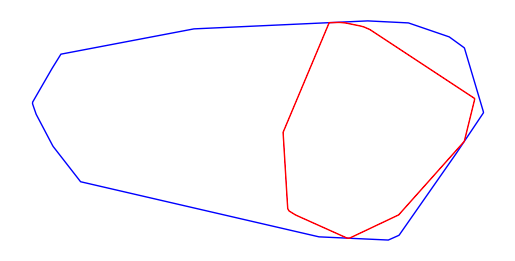
最適化後の多角形の様子

この図の赤色の枠内が今回提案した手法での「めぐろ」になります。
最適化がうまくできていそうですね。

結果

さあお待たせいたしました。
ここまでで作った「めぐろ」の領域を実際にマップに描画してみましょう。

geojson.ioという、地図上に任意の図を描画してくれるWebサービスがあります。
今回はこのサービスを使って実際にどのあたりが「めぐろ」と判定されているのかを見ていきます。
ここから「めぐろ」領域が見れます。

せっかくなので、今まで開催されてきた場所が「めぐろ」に入っているのかを確認してみた図が以下です。

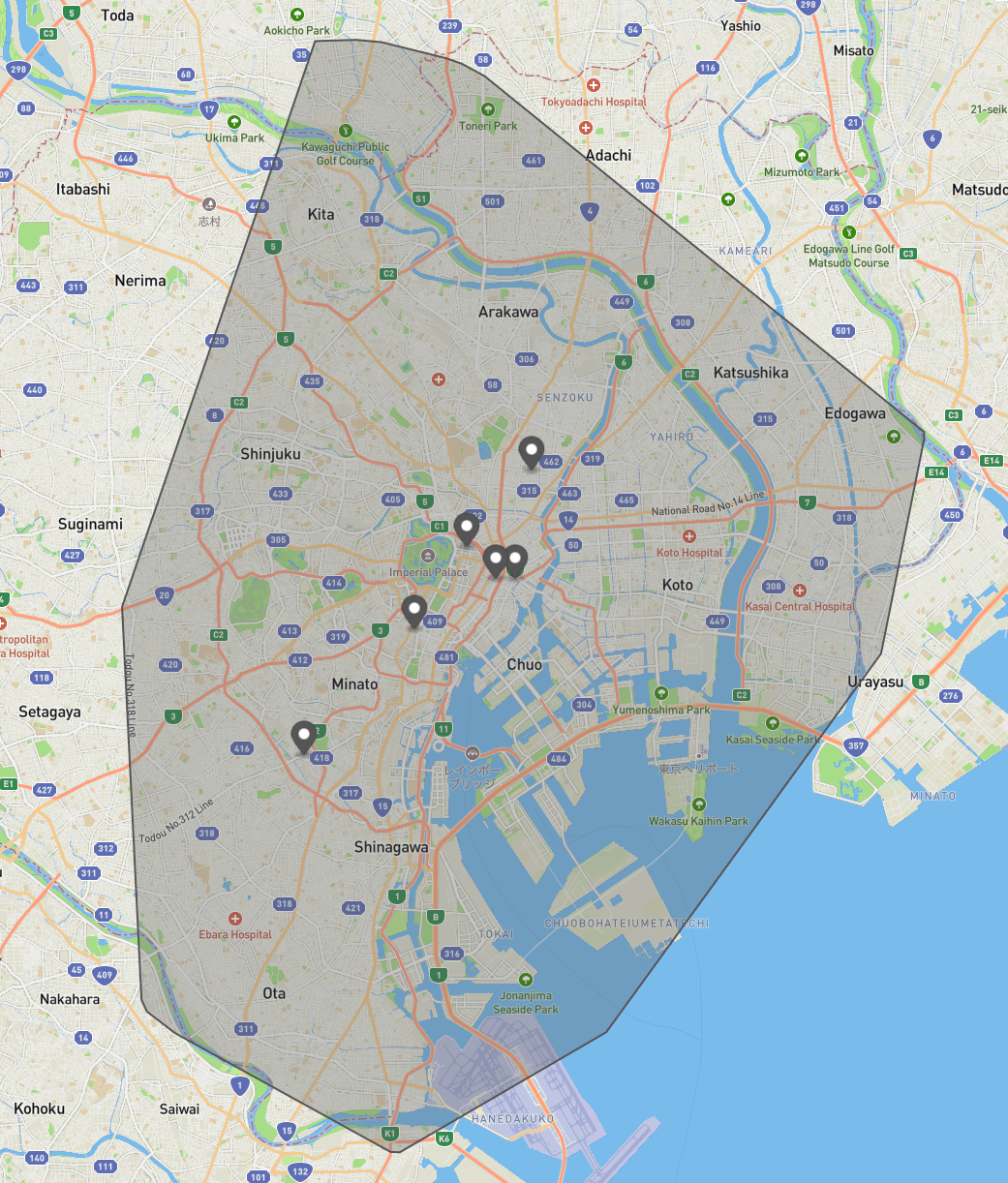
今までのめぐろLT開催地

いずれも「めぐろ」領域内に収まっていたことからも、この「めぐろ」領域はそれなりに納得感のあるものになったのではないでしょうか。

さいごに

というわけで運営の皆様、もしよければこの「めぐろ」領域を使うのはいかがですか？？
今後めぐろLTの開催地として名乗りを上げる方はぜひこのMapを活用して「めぐろ」領域内かどうかを確認してみてください。

余談

目黒と白黒って字が似てるなぁと思ったところから生まれたアイデアだったので、正直タイトルだけで満足しています。
最初はちゃんと東京全域で試したのですが、最適化後の結果が東京都の中央によってしまい目黒区が全然含まれなかったので、急遽ネオ東京案を構想しました。
今回対象外にした自治体は都合がいいようにそれっぽい理由と数値を付けて除外したのですが、どうしても町田市が左下に出っ張っているせいで凸包が広がってしまったため、テキトーな理由をつけて除外しました。ごめんね町田。

ちなみにこの記事を書いている最中に主催(?)であるラクスルさんの本社が2025年度より移転する旨のプレスリリースが出されましたが、移転先もちゃんと「めぐろ」領域内だったのでご安心ください。

Discussion