凸包アルゴリズム虎の巻~凸包定義編~

はじめに

本記事はNihon University Advent Calendar 2023の3日目の記事となっています。

自身の研究で凸包を使ってあれやこれやとする場面があったので、その凸包を求めるアルゴリズムとその実装について複数回にまたいでまとめていきます。
凸包アルゴリズム自体はいくつか存在しますが、この記事では最初凸包とは何かについてをまとめます。

凸集合とは

凸包を理解する前に「凸集合」とは何かを理解する必要があります。
凸集合は、めちゃくちゃ簡単に説明すると 「へこんでいない集合」 になります。
じゃあへこんでいるかどうかはどう判断するんだ。ということになると思いますが、言葉だけで説明すると 「与えられた集合の中からどの2点を取っても、その2点を結んだ線が集合の中にあれば凸集合である」 いえます。

ユークリッド空間の部分集合 $A \subset \mathbb R^n$ が凸集合であるための定義としては、以下を満たせばOKです。

$$\forall x,y \in A, \forall \lambda \in [0,1]:\lambda x + (1 - \lambda) y \in A$$

数式アレルギーの人向けの説明をすると

$\forall x,y \in A$:「与えられた空間の中から取り出した任意の2点を$x,y$として」
$\lambda \in [0,1]$：「$\lambda$を0〜1の間の値全てで」
$\lambda x + (1 - \lambda) y \in A$：「$x,y$間を$(1 - \lambda):\lambda$で内分した点が$A$に含まれていたらOK」

といった感じです。

図で見るとこんな感じになります。
集合$A$とその集合内の任意の2点を$x,y$としたとき、左側の図形は凸で、右側は凸ではありません。

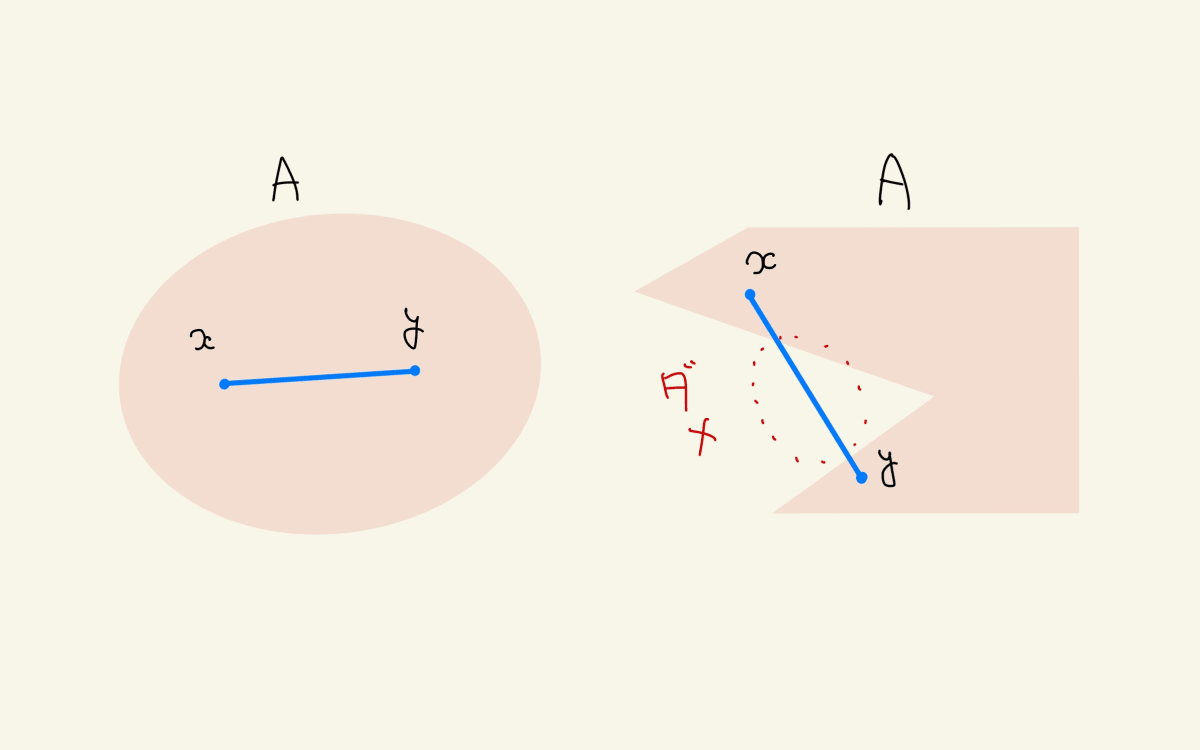
凸包とは

前置きが長くなりましたが凸包とは 「与えられた集合全てを含む最小面積の凸集合」 のことを指します。
与えられた集合が最初から凸集合であれば、その集合の凸包はその集合自身になりますが、凸集合でない場合にはその集合を全て含んだ上で面積が最小になる凸集合を考えなくてはいけません。

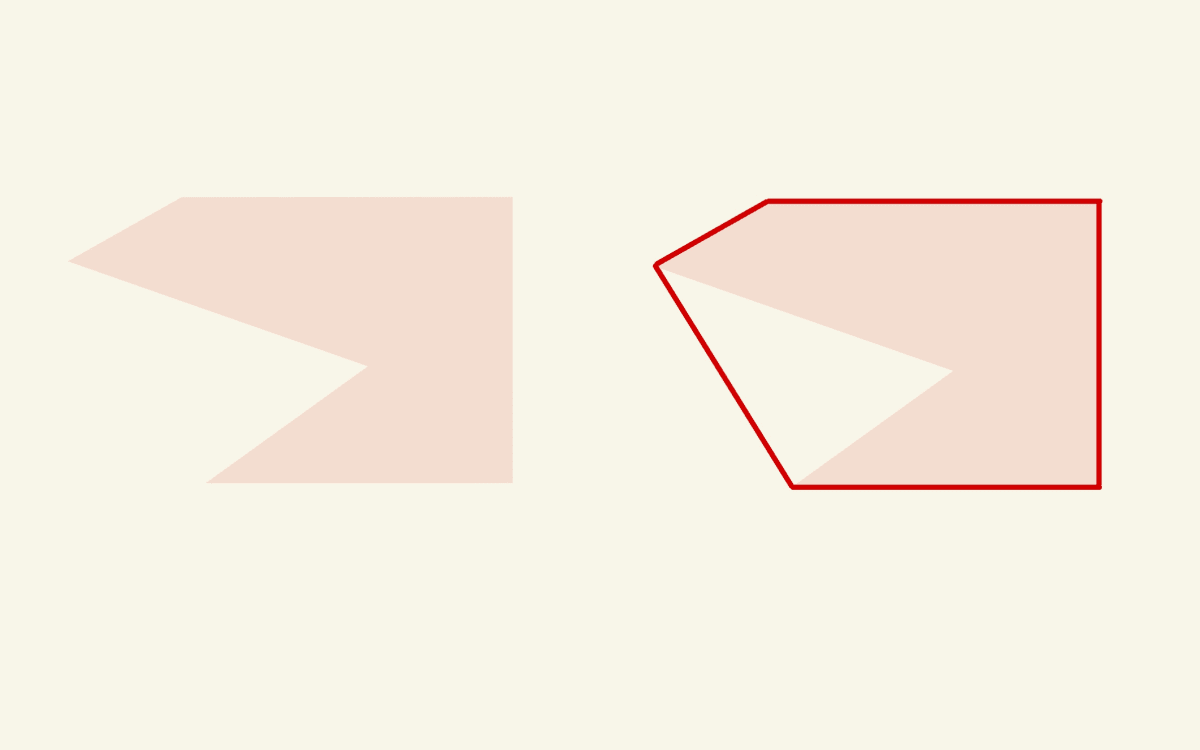
図で見るこんな感じになります。
左側の非凸の図形に対して凸包を取ると、右側の赤線の枠で囲われた図形になります。

終わりに

今回は凸包の定義についてまとめていきました。
次回は実際に与えられた点群から凸包を求める凸包アルゴリズムの一つである「Graham scan」についてまとめていこうと思います。