「AIはパターンマッチに過ぎない」論の誤解
はじめに
この頃Xでは「AIのやっていることはパターンマッチに過ぎない」という類の発言を多く目にします。調べてみるとこれは2025年6月にAppleから公開された"The Illusion of Thinking"をきっかに盛り上がった論調のようです。 ただ改めてこの論文に目を通したうえで少なくともこの論文を根拠にこの類の主張をすることには危うさがあると感じたのでその話を書きたいと思います。
論文の要約
この論文では一般に評価に使用されている数学やコーディングのベンチマークは
- 類似問題によるリークはおきている可能性がある
- 問題の複雑さを制御することができない
という理由から4種の論理パズル(ハノイの塔、チェッカージャンピング、川渡り、ブロックワールド)について複雑さ(ハノイの塔であればディスクの枚数)を変更して推論モデルがそれらに正答できるかどうかを検証しています。
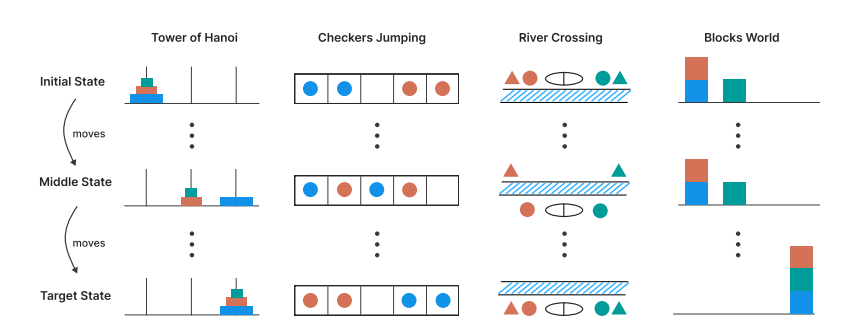
モデルが解き方を理解しているのであれば簡単なケースを正答できるのであればその複雑さを増やしても同様に解くことができるはずです。
しかしながら一定の複雑さを超えると推論モデルは正答できなくなるという結果となりました。

また実験結果から最小手数が31手であるn=5のハノイの塔が正答できるのにもかかわらず最小手数が11手であるn=3の川渡りが解けなかったという事実も指摘されています。
ここから推論モデルの汎化可能な問題解決能力に根本的な限界があることを明らかにしたとしています。
これはタイトルを踏まえると本来的な意味で推論を行っているのではなくAIは問題を丸暗記していてそれをパターンマッチング的に出力することで推論を行っているという趣旨かと思います。
批判
この論文について発表の3日後に"The Illusion of the Illusion of Thinking" という題でarxiv上で実験の設計に問題があるという指摘がされています。
ここでは指摘事項のいくつかを紹介します。
出力上限
以下の再現実験ではハノイの塔問題を解く際に「パターンは続きますが長くなりすぎないようにここで止めます」とモデルが発言していることが読み取れます。
実際に一定の複雑さを超えると出力できるトークン数の上限を超えてしまうようです。
またこれは推論時のトークン数が複雑さとともに増加するもののある地点からは逆に減っていくという挙動の根拠ともいえるでしょう。
最小手数と難易度
異なるパズルにおいて最小手数をもとに難易度を比較していることには問題があります。これは最小手数は分岐の有無などを踏まえると難易度と一致するわけではないためです。
実際に例に挙げられていたハノイの塔と川渡りの比較でもハノイの塔はパターンが明快なので一直線に解くことができるのに対して川渡りについては行き止まり、逆戻りを考慮して先を読む必要があって問題としての難易度は明らかに後者の方が高いです。
ハノイの塔が長手数でも解くことができるのはハノイの塔は有名問題のためモデルにとって既知であったからというよりもこの性質によるものでしょう。
その他
この他にもいくつかの致命的とも思える指摘がなされています。詳細はURLから確認してください。
根本的な問題
さらにいえば仮にこれらについて解決されたうえでなお同様の結果であったことを仮定しても推論モデルの問題解決能力に根本的な限界があることを明らかにしたといえるでしょうか?
ここで示された(と仮定した)ことはあくまでも論理パズルにおいて
- 一定の複雑さを超えると推論モデルは正答ができなくなる
- 有名問題であればマイナーな問題の簡単なケースより正答率が高いことがある
ということです。ここから
- 「AIのやっていることはパターンマッチに過ぎない」
- 「人間的な推論とは異なる」
と結論するのは妥当な推論でしょうか?
同じステップの繰り返しであったとしても一定の複雑さを超えるとそれが達成できなくなることや馴染みの問題であればある程度複雑な問題に関しても本来的な推論を辿ることなく正答してしまうということはむしろ人間的なふるまいのように自分には感じられます。
正しく"推論"したいものですね。
Discussion