ウェーブレット変換の考え方

解説事項

• ウェーブレット変換の考え方
• 連続ウェーブレット変換の式
• 短時間フーリエ変換との違い

離散ウェーブレット変換は次回扱います

ウェーブレット変換を一言で

• 時間・周波数解析の一種
• 信号を，Waveletと呼ばれる「非周期な小さな波」との内積で解析する
• ウェーブレット変換は短時間フーリエ変換と異なり，時間・周波数の解像度が周波数により変化する．

基本的なアイデア

ウェーブレット変換（Wavelet Transform）は，時間・周波数解析の一種である．
非周期な小さな波「Wavelet」を用意する．そのスケール（周波数）とシフト（時刻）を変えながら信号と内積をとる（下図）ことで，特定時刻の特定周波数成分が得られる．この波は内積をとる「核」として働き，これを「マザーウェーブレット」と呼ぶ．マザーウェーブレットとしてさまざまなWaveletが提案されている．

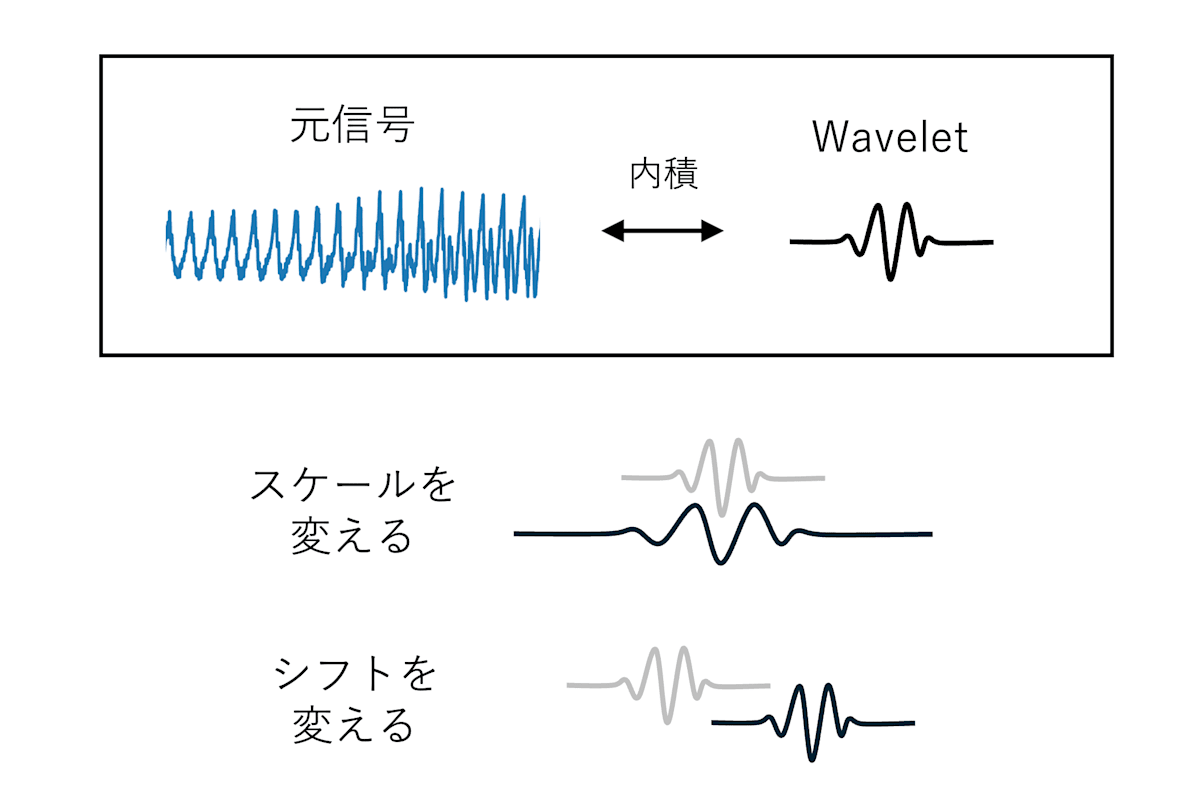
下図の通りその出力は，短時間フーリエ変換（STFT）と，結果的には近いものになる．しかし計算方法や特性には違いがある．

連続ウェーブレット変換(CWT)の式

CWTは，マザーウェーブレット$\Psi$のスケール$a$，シフト$b$を変えながら元信号 $x$と内積を取ることで成分を得る．スケール$a$が周波数，シフト$b$が時刻に対応し，その成分の強さを得られる．
※ $a$が大きいほど周波数は小さいことに注意

$$W(a,b)=\frac{1}{\sqrt{a}}\int^\infin_{-\infin}{x(t)\overline{\Psi \Big(\frac{t-b}{a}\Big)}}\, dt$$

次回解説する 「離散ウェーブレット変換」は多くの場合，単なる「連続ウェーブレットを数値計算する上での離散化」ではない．離散ウェーブレット変換は信号を帯域ごとの成分に冗長性なく分割するものであり，多重解像度解析と呼ばれる．

短時間フーリエ変換（STFT）との違い

内積をとる「核」が非周期という点がSTFTとの最大の違い

• STFTは信号に窓関数を掛けたのち，三角関数（周期）と内積をとる

STFTとCWTはどちらも時間周波数解析であり，時間解像度と周波数解像度のトレードオフが存在する（Wikiが詳しい）．STFTでは窓関数の幅により時間解像度が決まり，それにより全周波数帯域で同じ周波数解像度となる．一方でCWTは，周波数ごとに異なる時間・周波数解像度で行う（下図，出典）.

低周波成分ほど，低い時間解像度で高い周波数解像度になる．時間解像度の低下は，内積をとるウェーブレット関数が時間方向に広がることから，大まかなイメージを掴めるかもしれない．

さて，STFTに比べた連続ウェーブレット変換の利点はこの可変解像度にある．STFTで窓関数の幅$\Delta t$を固定すると，周期$\frac{\Delta t}{10}$の波なら10周期入る幅になり，その帯域は本来より細かい時間解像度を達成できたことになる．一方で周期$\frac{\Delta t}{10}$の時間解像度に合わせて時間窓を設定すると，全体の周波数解像度が損なわれることになる．それに対し連続ウェーブレット変換は，波長，言い換えれば波の最小単位に合わせて時間解像度が調整されるのが魅力的である．

次回 → 離散ウェーブレット変換

参考

• ウェーブレット変換の基礎と応用事例
• ウェーブレット変換の総まとめ
• 数理科学　ウェーブレットビギナーズガイド（東京電機大学出版局）