"ベイズ統計の理論と方法" を読んでいく

概要

ベイズ統計の理論と方法 を読んでいきます。

著作権上問題もあるのでテキストの要約というよりは、テキストを持っている前提で、行間を埋めていく形でメモしていきます。重要ではないことでも、個人的に気になった点に関しては掘り下げて書いているのでその点はご了承ください。重要なことでもテキストに明確に書いてあるものは省いています。個人的にテキストと一緒に読み返せるような読書メモのような位置付けです。

１　はじめに
２　基礎概念
３　正則理論
４　一般理論
５　事後分布の実現
６　ベイズ統計学の諸問題
７　ベイズ統計の基礎
８　初等確率論の基礎

私が持っているのは初版6刷のものです。ページ数などは刷数の関係で多少前後しているかもしれません。

正誤表について

私が持っている本は初版の6刷ですが、筆者のホームページにあるミスプリント情報は2刷目までのものしか反映されていません^[1]でした。ですので、本を読む際には以下のミスプリント情報をすべて適用していくことを強くお勧めします。定義式の間違いなどで気づきにくく混乱しにくいものも多数含まれているので、特に私のように慣れていない方は注意が必要です。

3刷ミスプリント
4刷ミスプリント
5~7刷ミスプリント Part1
5~7刷ミスプリント Part2
追加分ミスプリント

コロナ社の正誤表はこちら

そのほかに関してはこちらのスクラップで整理しています。

※ コロナ社の正誤表と筆者ホームページの正誤表は大体一緒だが一部は片方にしかないようなものがそれぞれ存在するので注意が必要です。全部見るしかなさそうです。

脚注

1. 厳密には4刷ミスプリントの一部は反映されていました。途中で一部変更が巻き戻ったりしている可能性が高いと考えます。状況が整理できれば出版社にも連絡する予定です。 ↩︎

１　はじめに

ベイズ統計における統計的推測の考え方や基本的な概念の定義などが行われている。

定義(最低限)

テキストにならって、記号などの概念の定義をここで整理しておく。ちらっとみたときになんとか意味がわかる程度にしておく。基本的にはテキスト通りなので、詳細はそちらを参照する。

N, n \in \mathbb{N} に対して、N 次元ユークリッド空間 \mathbb{R}^N 上のn個の点^[1]

x_i \in \mathbb{R}^N \quad (i = 1,2,\ldots, n)

の集合をサンプルと呼び、

x^n = (x_1, x_2, \ldots, x_n) \in (\mathbb{R}^N)^n

と書く^[2]。このサンプルそれぞれは 真の分布 q(x) に独立に従う確率変数の実現値と考えることとする。この q(x) は以下のように柔軟に記号が使われるので注意する。

q(x^n) = \prod^n_{i=1} q(x_i)

つまり、q は、\mathbb{R}^N 上で定義される関数であるが、自然に (\mathbb{R}^N)^n 上でも定義される。ほとんど誤解がないと思うので、テキストに習って同じように書くことにする。

また、q(x)の分布を持つ確率変数を

X^n = (X_1, X_2, \ldots, X_n)

とする。

パラメータ w \in W \subset \mathbb{R}^d における x \in \mathbb{R}^N 上の条件付き確率分布 p(x|w) を確率モデルと呼び、 w \in W 上の確率分布 \varphi(w) を事前分布という。

また、

p(w|X^n) = \frac{1}{Z_n(\beta)} \varphi(w) \prod^n_{i=1} p(X_i|w)^\beta

をパラメータ w の事後分布と呼び、0 < \beta < \infty で定義される \beta を逆温度 と呼ぶ。一般的な教科書では、\beta = 1で議論することが多いのでこの点は注意が必要である。

Z_n(\beta) は規格化定数のような存在で、分配関数と呼び、

Z_n(\beta) = \int_W \varphi(w) \prod^n_{i=1} p(X_i|w)^\beta dw

と定義される。さらに、

F_n(\beta) = - \frac{1}{\beta} \log Z_n(\beta)

とする。また、これを自由エネルギーと呼ぶ。

脚注

1. 実践的にはN次元の実数値のデータ一つと点が一つ対応していると考えて良さそう ↩︎

2. 実践的にはnのデータセットと対応していると考えて良さそう ↩︎

埋めたい「行間」

逆温度

p.3 で突然に(逆)温度という物理的な量が出てくる。これは数学的構造が熱力学や統計力学と似ているためにアナラジーとして名付けたと推測できるが真意はわかっていない。

物理学においては、逆温度というのは温度の逆数を表す物理量である。統計力学では、ミクロな状態(粒子のエネルギーなど)は分布をもっており、それらとマクロな状態(温度、圧力など)の関係性を調べることが一つの目的になっている。実際、温度が一定の系においては、その分布(カノニカル分布と呼ぶ)がミクロな状態(\omega)の関数であるエネルギー(E(\omega))を使って

p(\omega) = \frac{1}{Z(\beta)} \exp(-\beta E(\omega))

と表される。\beta は、もちろん物理的な意味での逆温度(\propto \frac{1}{T})である。Z(\beta) も分配関数であり、これらの用語は統計力学が起源ではないかと思われる。ちなみに、カノニカル分布は、指数型分布であるので(テキストで書かれていた)良い性質をもった分布である点は興味深い^[1]。

章末問題 【1】 の証明において、 L_n(w) は最小値とると言えるのか？

章末問題【1】は次のような問題である。

次の等式が成り立つことを示せ。

\inf_\beta F_n(\beta) = \inf_{w \in W} \{ - \sum^n_{i=1} \log p(X_i|w) \}

テキストの解答では、最初に

L_n(w) = - \frac{1}{n} \sum_{i=1}^n \log p(X_i | w)

を定義し、 L_n(w) を最小にするパラメータを \hat{w} とおいて議論が進められている。一般には \inf (下限)があるからといって最小ではないので、これは一般の w \in W に対しては成り立たない。

テキストでは w の集合である W に制約は課されていないので、常に最小値があるとは一般にはいえない。逆に最小値を取るための条件はどうなるかというと、W がコンパクト集合の場合 になる。一般に、コンパクト集合上の連続関数は最大値・最小値を持つことが知られているので、この解答では暗に W がコンパクトであること ^[2]が仮定されていると解釈するべきだと考えられる。

そこまでわかると気になることは次の2点。

1. W がコンパクト(有界閉集合)という仮定は、応用の観点から現実的なのだろうか？
2. W がコンパクト(有界閉集合)でなくても、問題の等式は成立する？(正しい証明は？)

1. について

確率モデルのパラメータ w は、実在するものと対応するケースとそうでないケースがあると考える。

例えば、テストの点数について推論をしたいとき、平均 \mu をパラーメータとする正規分布を確率モデルとおいたとする。\mu はテストの点数と対応づけられるので、実在するもの対応するケースに当てはまると考えられる。そして、このとき、テストが0点から100点までで採点されるものの場合、0 \leq \mu \leq 100 とすることができる。こういうケースにおいては、テストの点数の範囲がそもそも有界閉で定義されているので、パラーメータ w も有界閉集合で定義されることが多いと思われる。

実在するものと対応しないようなパラメータの場合は、人為的なものなのでどちらでも取ることができる。ただ、計算機で計算する都合上、有界閉集合に取ることが多くなると思われる。

どちらにせよ、W をコンパクトと仮定するのは応用上はそんなに問題にはならなさそうだと考えているが、応用について深く知らないのでなんともいえないところは残る。(が、ここでの考察はここまでとする)

2. について

実は「L_n が最小値を持つ」ことは、一般には成り立たないが章末問題の等式は成立する。そのためには、テキストの証明の一部を修正する必要がある。^[3]

具体的には、次のようにする。

L_n(w) = - \frac{1}{n} \sum_{i=1}^n \log p(X_i | w)

を定義する。(ここまではテキストと同じ)
ここで、L_n(w) に下限が存在することから、L_n(w_1) > L_n(w_2) > \ldots > L_n(w_n) > \ldotsとなる数列\{w_i\}を構成することができる。また、L_{n,i} = L_n(w_i) として、数列 \{L_{n,i}\} を考えると、これは下に有界な単調減少する数列である。下に有界な単調減少する数列は下限値に収束するので、この値を \hat{L_n} とする。つまり、

\hat{L_n} = \lim_{i \to \infty} L_{n, i}

である。この \hat{L_n} をテキスト中のL_n(\hat{w})と読み替えれば同じように証明できる。

脚注

1. テキストでも「自然科学や情報科学において現れる確率分布は P(x) \propto \exp(-E(x)) の形をしていることが多い」と記載がある。カノニカル分布も念頭にあったに違いない。 ↩︎

2. 一般に有限次元のユークリッド空間においては、「コンパクト \iff 有界閉」であり、今回はW \subset \mathbb{R}^d であるので、「W がコンパクトであること \iff W が有界閉集合であること」である。具体的には、d = 1 とすると、例えば[0, 100] などの閉区間であれば、テキストの解答の方法が使えるということになる。 ↩︎

3. おそらく、筆者はこれも分かった上で簡略化した証明を解答として載せていると思われる。実践的にはコンパクトなことがほとんどでかつ、証明方法自体も実質的には変わらないので、「だいたいわかるでしょ」という部分なのかもしれない。 ↩︎

１　基礎概念

ベイズ統計理論の構築に向けて、真の分布と確率モデルの関係の分類や各種概念の定義がなされている。

定義(最低限)

思い出すように記載。基本的にはテキストを確認する。

平均対数損失関数

L(w) = - \mathbb{E}_X [ \log p(X|w) ]

経験対数損失関数

L_n(w) = - \frac{1}{n} \sum_{i=1}^n \log p(X_i|w)

実現可能なパラメータの集合

W_{00} = \{ w \in W ; \text{すべての} x \text{について} q(x) = p(x|w) \}

最適なパラメータの集合

W_0 = \{ w \in W ; L(w) \text{が最小値をとる} \} = \underset{w \in W} {\operatorname{argmin}} \, L(w)

汎化損失

G_n = - \mathbb{E}_X [ \log \mathbb{E}_w [p(X|w)] ]

経験損失

T_n = - \frac{1}{n} \sum_{i=1}^n \log \mathbb{E}_w [p(X|w)]

対数尤度比関数

f(x, w_0, w) = \log \frac{p(x | w_0)}{p(x | w)}

w_0 \in W_0 で最適な分布が実質的にユニークな場合、f(x, w_0, w) の w_0 は依存から外れるので、 f(x, w) と書く。

平均誤差関数

K(w) = \mathbb{E}_X [ f(X, w) ]

経験誤差関数

K_n(w) = \frac{1}{n} \sum_{i=1}^n f(X, w) ]

汎化損失のキュムラント母関数

\mathcal{G}_n(\alpha) = \mathbb{E}_X[\log \mathbb{E}_w [p(X|w)^\alpha]]

経験損失のキュムラント母関数

\mathcal{T}_n(\alpha) = \frac{1}{n} \sum_{i=1}^n \log \mathbb{E}_w [p(X|w)^\alpha]

埋めたい「行間」

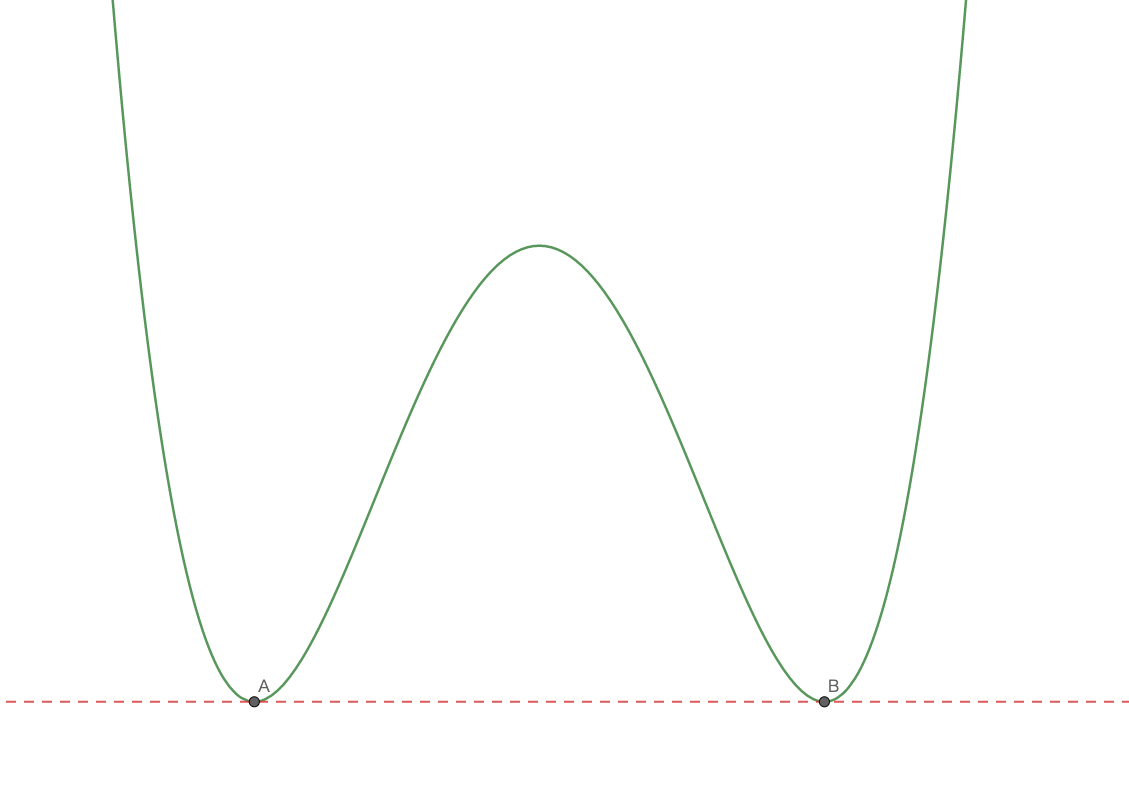
p.31 注意11 の具体例の確認

W_{00} の元が複数個あるとき、p(x|w) は w \in W_{00} に依存しないが、微分の値は w に依存して異なる。真の分布が確率モデルで実現可能な場合であっても、統計的に推測されるパラメータは真のパラメータとぴったりとは一致せず、... 微分構造を考慮する必要がある

とあるが、この点を例を挙げて確認しておく。

p(y|x, a, b) = \frac{1}{\sqrt{2 \pi}} \exp( - \frac{1}{2}(y - a \sin (bx))^2)

という確率モデルを考える。このとき、真の分布が

p(y|x, a, b) = \frac{1}{\sqrt{2 \pi}} \exp( - \frac{1}{2}(y - \sin (x))^2)

であるとすると、W_{00} = \{(1, 1), (-1, -1)\} である。a \sin(bx) が (a, b) = (1, 1) のときも (a, b)=(-1, -1) のときも \sin x になることから確認できる。つまり、

p(y | x, 1, 1) = p(y | x, -1, -1) = q(x)

である。ここで、\frac{\partial}{\partial a} \log p(y|x, a, b) をW_{00} の二つの元で評価してみる。

\begin{aligned} \frac{\partial}{\partial a} \log p(y|x, a, b) &= \frac{1}{p} \cdot p [-(y - a \sin(bx)](- \sin(bx)) \\ &= (y - a \sin(bx)) \sin(bx) \end{aligned}

であるので、

\begin{aligned} \frac{\partial}{\partial a} \log p(y|x, 1, 1) &= (y - \sin(x)) \sin(x) \\ \frac{\partial}{\partial a} \log p(y|x, -1, -1) &= - (y - \sin(x)) \sin(x) \end{aligned}

となる。ちょうど符号が反転しており、W_{00} の元であっても微分構造が異なるものがあることを確認できる。

p.32 正則の定義の注意点

W_0の要素 w_0 が一つだけであり、w_0 を含む開集合で W に含まれるものが存在していてかつ、w_0 でのヘッセ行列 \nabla^2 L(w_0) ... が正則(固有値がすべて正の値であること)であるとき、q(x) は p(x | w) に対して正則であるという

とある。ヘッセ行列が正則というのは、固有値がすべて正の値であることと等しいということなので、一般には正定値行列と呼ばれるものである。^[1]

ヘッセ行列が正定値行列であること以外の重要な条件として W_0の要素 w_0 が一つだけ というものがあるつまり、最適なパラメータは唯一であるということである。2次元グラフで表すと以下のような L(w)、W_0 の場合は、点A、B の2点が最適なパラメータになっているので、正則であるとは言えない。

脚注

1. ヘッセ行列が正則、という表現を他で使われているかどうかの確認は出来なかった。正則の言葉がダブっていることを踏まえると誤植の可能性もあるかもしれない。 ↩︎

p.32 カルバック・ライブラ擬距離が0のとき、関数として q(x) = p(x | w) が成立することの証明

真の分布と確率モデルのカルバック・ライブラ距離...はつねに非負であり、0になるのは q(x) = p(x | w)が成り立つ時に限る。

とあるが、証明を確認しておく。カルバック・ライブラ擬距離^[1]が非負であり、0になるのは q(x) = p(x | w)が成り立つ時に限ることを示す。

一般に以下の対数関数において成立する不等式が成立することを利用する。

\log x \leq x - 1

等号成立条件は x = 1 である。これを用いて、カルバック・ライブラ擬距離の表式を変形させる。

\begin{aligned} \int q(x) \log \frac{q(x)}{p(x | w)} dx &= - \int q(x) \log \frac{p(x | w)}{q(x)} dx \\ &\geq - \int q(x) (\frac{p(x | w)}{q(x)} - 1) dx \\ &= - \int (p(x | w) - q(x)) dx \\ &= \int q(x) dx - \int p(x | w) dx \\ &= 1 - 1 = 0 \end{aligned}

等号成立条件は、すべての x ^[2] において、q(x) = p(x | w) が成立することである。以上で、カルバック・ライブラ擬距離が非負であり、0になるのは q(x) = p(x | w)が成り立つ時に限ることがわかった。

脚注

1. カルバック・ライブラ擬距離は、距離の定義に当てはまらないので擬距離と表現されることがある。テキストでは距離と書かれているが、誤解が生まれにくいようにこのスクラップでは擬距離と書くことにする。 ↩︎

2. 厳密には almost everywhere で十分(例えば、有限個の点で q(x) = p(x | w) が成立していなくても、積分の値は変わらないので、等号は成立する) ↩︎

p.38 F(t) = \frac{t^2}{2} \exp(-t^{\ast}) \, (|t^\ast | < |t|) の導出

F(t) = t + e^{-t} - 1

というF(t)を、|t^\ast | < |t|となる t^\ast を用いて

F(t) = \frac{t^2}{2} \exp(-t^{\ast})

が成り立つことが、平均値の定理より成り立つと書かれていたが、導出方法を確認しておく。

F(t) は十分になめらかな関数であるので、テイラーの定理とラグランジュの剰余項の表式より、0 < t^\ast < t となる t^\ast を用いて次のように書ける。

\begin{aligned} F(t) &= F(0) + F'(0) t + \frac{1}{2} F''(t^\ast) t^2 \\ &= \frac{t^2}{2} \exp(- t^\ast) \end{aligned}

一方で、-t < - t^\ast < 0 としても同様の式が得られるので、|t^\ast | < |t|となる t^\ast を用いて

F(t) = \frac{t^2}{2} \exp(-t^{\ast})

が成立する。テイラー定理におけるラグランジュの剰余項を求める際に平均値の定理が必要になっている。もしかしたら、もっと直接的に平均値の定理で上記は証明できるかもしれないが、良い方法がわからなかった。

p.47 補題8 の証明

• 命題

c_2 = 2, c_3 = 6, c_4 = 26 とすると、 k = 2,3,4　において以下が成立する

|\mathcal{G}^{(k)}_n(\alpha)| \leq c_k \mathbb{E}_X \left[ \frac{\mathbb{E}_w[|f(X, w)|^k \exp (- \alpha f(X, w))]}{\mathbb{E}_w[\exp (- \alpha f(X, w))]} \right] \\ |\mathcal{T}^{(k)}_n(\alpha)| \leq c_k \frac{1}{n} \sum_{i=1}^n \frac{\mathbb{E}_w[|f(X, w)|^k \exp (- \alpha f(X, w))]}{\mathbb{E}_w[\exp (- \alpha f(X, w))]}

• 補足する部分

(要約) 以下のヘルダーの不等式の結果と補題7と注意19とから補題8が得られる

\mathbb{E}^{(\alpha)}_w[|f(A, w)|^j] \geq \mathbb{E}^{(\alpha)}_w[|f(A, w)|^k]^{j/k}

ただし、j \leq k であり、

\mathbb{E}^{(\alpha)}_w[g(A, w)] \equiv \frac{\mathbb{E}_w[g(X, w) \exp (- \alpha f(X, w))]}{\mathbb{E}_w[\exp (- \alpha f(X, w))]}

とする。

この省略されている部分を少し丁寧に追いかけておく。

最初に \mathcal{L}_k(X) に関して次の不等式が成立することを確認しておく。

\mathcal{L}_k(X) = \frac{\mathbb{E}_w[(-f(X, w))^k \exp (- \alpha f(X, w))]}{\mathbb{E}_w[\exp (- \alpha f(X, w))]} \leq \mathbb{E}^{(\alpha)}_w[|f(A, w)|^k]

k = 2 のときから考える。補題7より

\mathcal{G}_n^{(2)}(\alpha) = \mathbb{E}_X [\mathcal{L}_2(X) - \mathcal{L}_1(X)^2]

が成り立つ。

ヘルダーの不等式の結果において、j = 1, k = 2 と置くと、

\mathbb{E}^{(\alpha)}_w[|f(A, w)|] \leq \mathbb{E}^{(\alpha)}_w[|f(A, w)|^2]^{1/2}

より

\mathbb{E}^{(\alpha)}_w[|f(A, w)|]^2 \leq \mathbb{E}^{(\alpha)}_w[|f(A, w)|^2]

である。したがって、

\begin{aligned} \mathcal{L}_1(X)^2 &= \left( \frac{\mathbb{E}_w[(-f(X, w)) \exp (- \alpha f(X, w))]}{\mathbb{E}_w[\exp (- \alpha f(X, w))]} \right)^2 \\ &\leq \mathbb{E}^{(\alpha)}_w[|f(A, w)|]^{2} \\ &\leq \mathbb{E}^{(\alpha)}_w[|f(A, w)|^2] \end{aligned}

となる。最後の行でヘルダーの不等式の結果を使った。

以上より、

\begin{aligned} \mathcal{G}_n^{(2)}(\alpha) &= \mathbb{E}_X [\mathcal{L}_2(X) - \mathcal{L}_1(X)^2] \\ &\leq \mathbb{E}_X [|\mathcal{L}_2(X) - \mathcal{L}_1(X)^2|] \\ &\leq \mathbb{E}_X [|\mathcal{L}_2(X)| + |\mathcal{L}_1(X)^2|] \\ &\leq \mathbb{E}_X^{(\alpha)}[|f(A, w)|^k] + \mathbb{E}_X^{(\alpha)}[|f(A, w)|^k] \\ &= 2 \mathbb{E}_X^{(\alpha)}[|f(A, w)|^k] \end{aligned}

が導かれる。途中の変形で三角不等式を使った。これは k = 2 (c_2 = 2) のケースになっている。

k = 3,4 についても \mathcal{T}_n^{(k)}(\alpha) についても同じ方針で導くことが出来る。

３　正則理論

p.60 補題10 の説明

確率過程 \eta_n(w) を以下のように定義する。

\eta_n(w) = \frac{1}{\sqrt{n}} \sum^n_{i=1} (K(w) - f(X_i, w))

このとき、\eta_n(w) と同じ平均関数と相関関数を持った正規確率過程を \eta(w) とすると、\eta_n(w) は \eta(w) に法則収束する。

というのが補題10であった。

説明は 8.5.3 の紹介に留めているので、この部分を少し確認する。
8.5.3 に書かれている中でこの補題に関わる部分は以下の2点。

• コンパクト集合上の正規確率過程は、平均関数と相関関数が決まるとユニークに定まる
• 経験過程は、同じ平均関数と相関関数を持った正規確率過程に法則収束する^[1]

そして、\eta_n(w)は、有限性に関する2つの条件(テキストの(8.5), (8.6))を満たせば、経験過程と言える。したがって、この補題10が成り立つ。これらの証明などに関しては、余力があれば 8 章を読んでいく中で確認することにする。

脚注

1. この事実は、関数空間での中心極限定理と呼ばれているとのこと。 ↩︎

p.63 J(w) は w_0 近傍で正則であることの証明

補題13 の証明の中で、平均対数損失関数 L(w) のヘッセ行列 J(w) が w_0 の近傍で正則であることを利用していた。この章は正則理論を扱っているので、前提として、w の空間 W はコンパクトで、w_0 は J の最小値を与える唯一の元である。

w_0 だけでなく、その近傍でもヘッセ行列が正則であることは、直感的には言えそうだが、パッと証明できなかったのでここにメモとして残す。

J(w) は w の連続関数になっている。また、\textrm{det} も連続である。一方で、\textrm{Ker}(\textrm{det}) が非正則行列の集合と一致する。\textrm{det} の値域である \mathbb{R} において \{0\} は閉集合であるので、非正則行列の集合も(\textrm{det}の定義域における正方行列の集合において)閉集合になる。したがって、J(w) が非正則となるような w の集合も閉集合になる。

したがって、 J(w_0) が正則であれば、J(w) は w_0 の(開)近傍において正則になることがわかる。

同じような議論で一般に、非正則行列の列は正則行列には収束しないことも証明できる(n次の正方行列の距離を \mathbb{R}^{2n} におけるユークリッド距離とみなしている)^[1]

非正則行列は \textrm{det} によって、1点に詰め込まれてしまうような特殊な存在だということは、イメージとして捉えておくと、この手の証明もすぐに浮かぶようになるかもしれない。

脚注

1. このことは Twitter で@mo20211201さんに教えていただいた ↩︎

p.62 補題13 のざっくりとした理解

補題13 の計算は置いておいて、ざっくりとした理解を整理しておく。

K(w_0) = 0 \\ \nabla K(w_0) = 0

なので、K(w) は w_0 の近傍では (w - w_0)^2 が支配的でその係数がヘッセ行列\frac{1}{2} Jとなっている。

一方で、

K_n(w) = K(w) - \frac{1}{\sqrt{n}}\eta_n(w)

であり、補題10より\eta_n は平均関数が0、対数尤度比の相関関数を持つ正規確率過程に n \to \infty で法則収束する。したがって、主要項 Z_n^{(1)}(\beta) の非積分関数は、平均が w_0 + O(1/\sqrt{n})のG分布になるとざっくり考えることができる。積分領域は K(w) < \epsilon であり、

\lim_{n \to \infty} \sqrt{n} \epsilon = \infty

であるので、n \to \infty を考えたとき、平均が積分領域よりも速く収束 していく。そのため、極限ではガウス分布の積分は全域での領域とほぼ同等となる。

p.75 事後確率最大化推定量、最尤推定量、平均パラメータの違い

注意28 で真の分布が正則であり、事後分布が正規分布で近似できる場合、1/\sqrt{n}の項まで等価で、ほとんど差が出ない。これは、 正則理論の範囲では、これらの精度の差がほぼないということを意味している。「ほぼない」と書いたが、 n は十分大きいと思うと 1/\sqrt{n} の精度まで同じなので、実際的な観測上は差がないと考えて良いだろう。

p.75 定理5 の証明の補足

\nabla^2 L(w^{*}) = J + o_p(1)

定理5 の証明の中でこれがさらっと書かれていたが、パッとわからなかったので補足しておく。
p.63 で議論されているように、

w^{*} = w_0 + o_p(1) \\ J(w^{*}) = J + o_p(1)

であり、 \nabla^2 L(w^{*}) = J(w^{*}) であるので、これが成り立つ。 (J(w) はヘッセ行列 \nabla^2 L(w)であることを思い出しておく)

p.75 定理5 の解釈

定理5より

L(\hat{w}) = L(w_0) + \frac{1}{2n} || \xi_n ||^2 + o_p(\frac{1}{n}) \\ \quad \\ L_n(\hat{w}) = L(w_0) - \frac{1}{2n} || \xi_n ||^2 + o_p(\frac{1}{n})

である。L(w) は w_0 で最小値を取る。\hat{w} は w_0 から少し離れた位置にあるので、大雑把に言って第二項の分だけ、最小値から大きくなる。逆に、L_n(w) は \hat{w}で最小値を取るので、同じように第二項の分だけ最小値から大きくなる(ただし、左辺が \hat{w} を使ったものになっているので、符号が逆になっている)。

また、平均対数損失関数と経験対数損失関数は第二項の2倍になっており、これも \frac{1}{n} に比例するので、サンプル数が大きくなることでほぼ一致しているといえる。