[Unity] 数式を読み解きながら頂点シェーダーで波の動きを作ってみる(Gerstner Waves)

1. はじめに

波の動きを作るために Gerstner Waves というものがあります。

https://developer.nvidia.com/gpugems/gpugems/part-i-natural-effects/chapter-1-effective-water-simulation-physical-models

上記のサイトで詳しく知ることができます。他にも先人の技術ブログがいくつもあるのでそちらも参考になるかと思います。

自分で実装してみて「なるほど！！すごい！！」と思ったので、昔からある技術ではありますが今回は私なりの解説で紹介してみたいと思います。

実装はUnityのサンプルプロジェクトをGithubに公開しています。
https://github.com/ner-develop/GerstnerWaves

2. 波の合成

まずは Gerstner Waves でも基本となる波の性質についてです。波の合成は「重ね合わせの原理」として高校物理で習った記憶があります。覚えてる方もいると思いますが、おさらいとして簡単に触れておきたいと思います。

よく物理の調べ物でお世話になる金沢工業大学さんのページを貼っておきます。

https://w3e.kanazawa-it.ac.jp/math/physics/high-school_index/wave/henkan-tex.cgi?target=/math/physics/high-school_index/wave/superposition_of_wave.html

波の合成の図を用意しました。

• 赤色: Sin波1
• 青色: Sin波2
• 緑色: Sin波1 + Sin波2

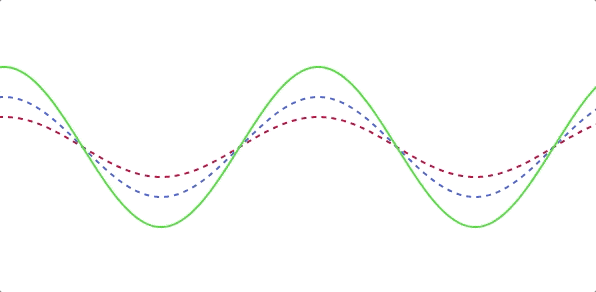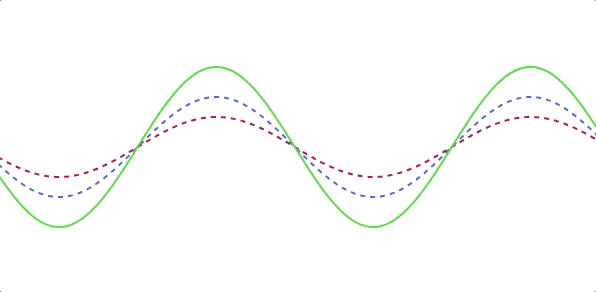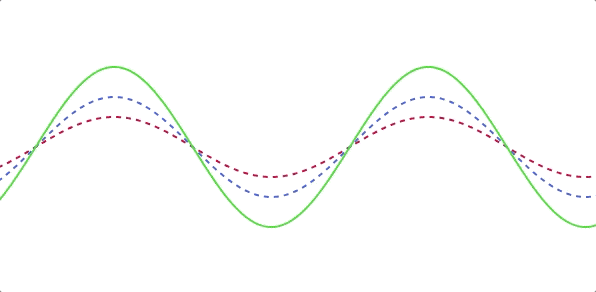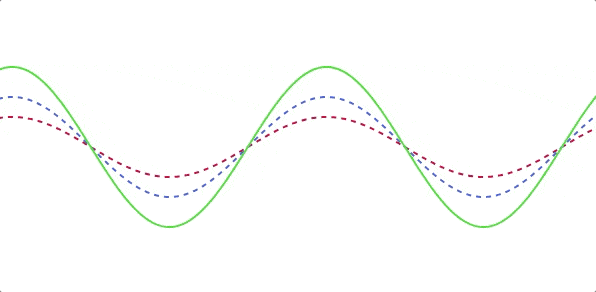
ただ足し算をしているだけです。上図は動いていますがある時間で止めて振幅を見ると足し算されているのが分かります。

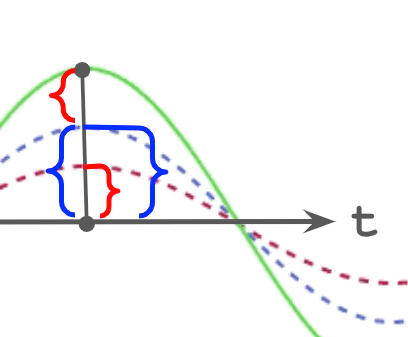
例としてSin波を使っていますが、矩形波だろうがなんだろうが合成はただ足すだけです。物理で学ぶような水面の波も音波も、この「重ね合わせの原理」という性質を持っています。

逆に考えると、「複雑な波」は分解すると「複数の単一波」を足し算した波と考えることができます。先ほどの図は足し算がわかりやすいように赤波と青波は振幅しか変えていませんでしたが、下図では位相や周期も変えて合成してみます。

規則正しさが消えて、ちょっと複雑な波になりました。こんな感じで、実際の水面の波も単一の波をたくさん合成した複雑な状態になっています。お風呂の中でちゃぽんと単一波を異なる場所でたくさん起こしてみるとさらにイメージしやすいかもしれません。

3. Gerstner Waves

それでは本題に入っていきます。Gerstner Wavesも最終的には先ほどのように「波の合成」をして、複雑な波を表現します。ですが、まずは基本となる「単一の波」に焦点を当ててみていきます。

3.1. 仕組み

波の合成の説明ではSin波を使いました。Sin波は単位円における、角度が変化した際の縦軸の値を出力したものであり、軌跡は円運動となります。(Cos波は横軸の値を出力したものですが、同じ円運動ですので位相がずれただけと言えます)

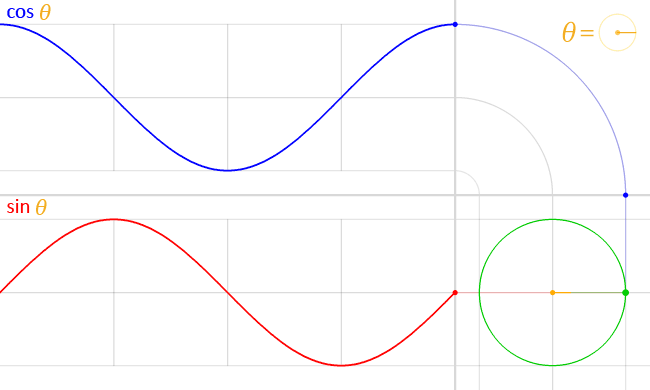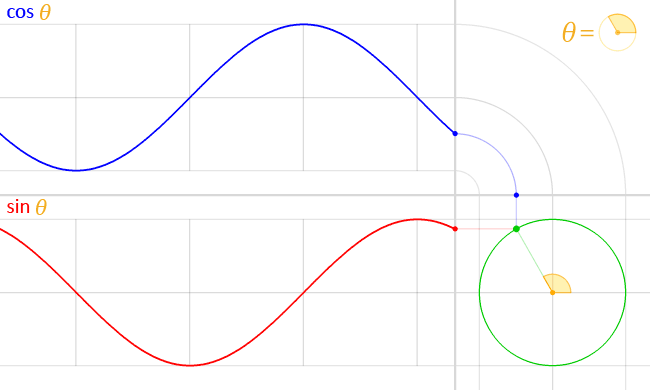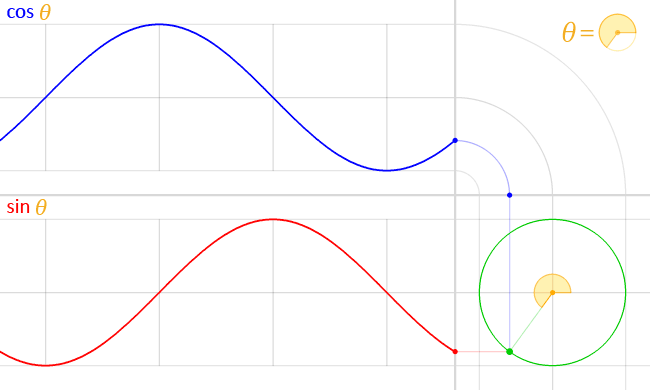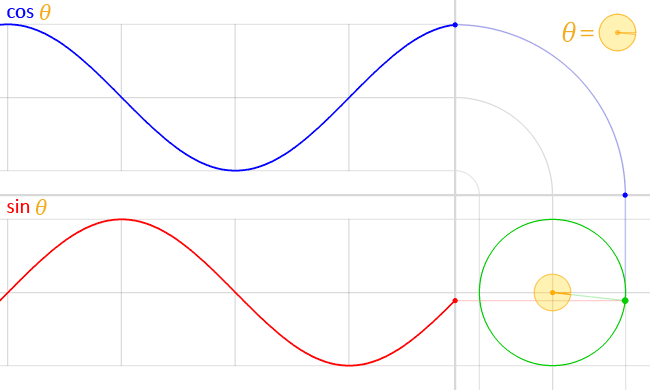
画像引用: https://ja.wikipedia.org/wiki/三角関数

なので、そもそもSin波は円運動の軌跡であり、海の波を表現しているわけではありません。波をSin波を使った数式で表すのは簡単でそれっぽくは見えるものの、やっぱり波としては物足りません。

ではどうしたら波っぽく見えるのかというと、密度の差です。Wikipediaにとても分かりやすいGif画像があるので引用させていただきます。山になっている部分は密度が高く尖り、谷の部分は密度が低くなだらかになっています。

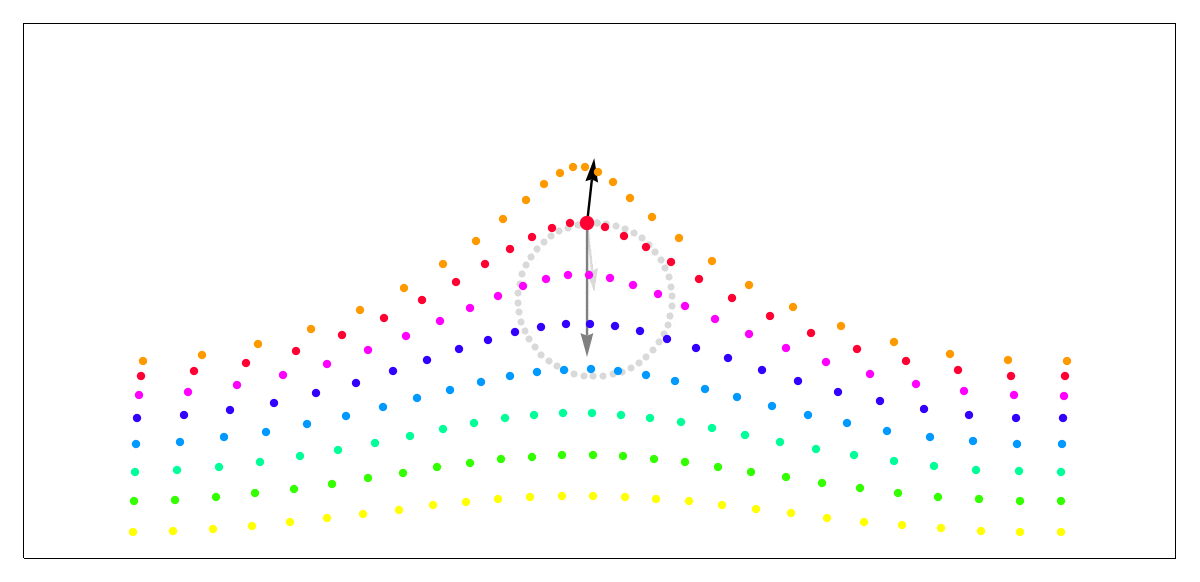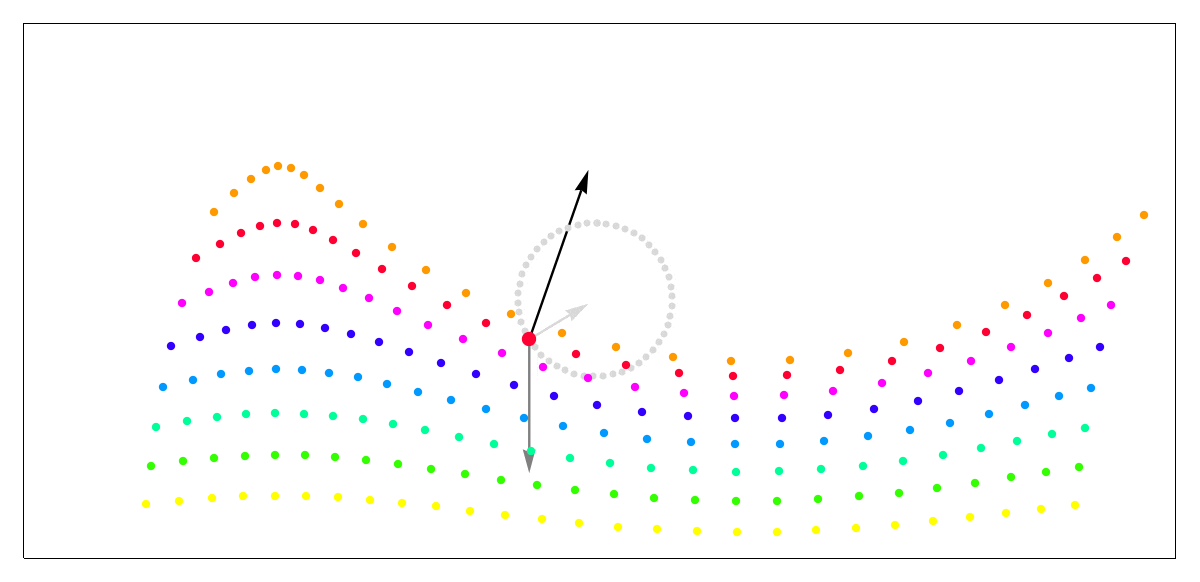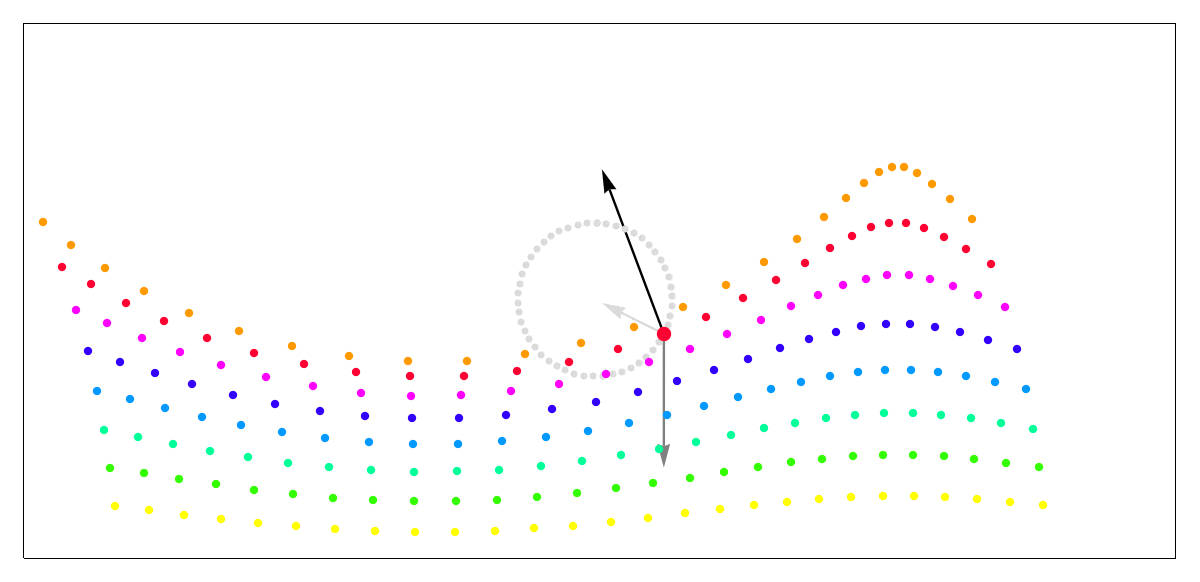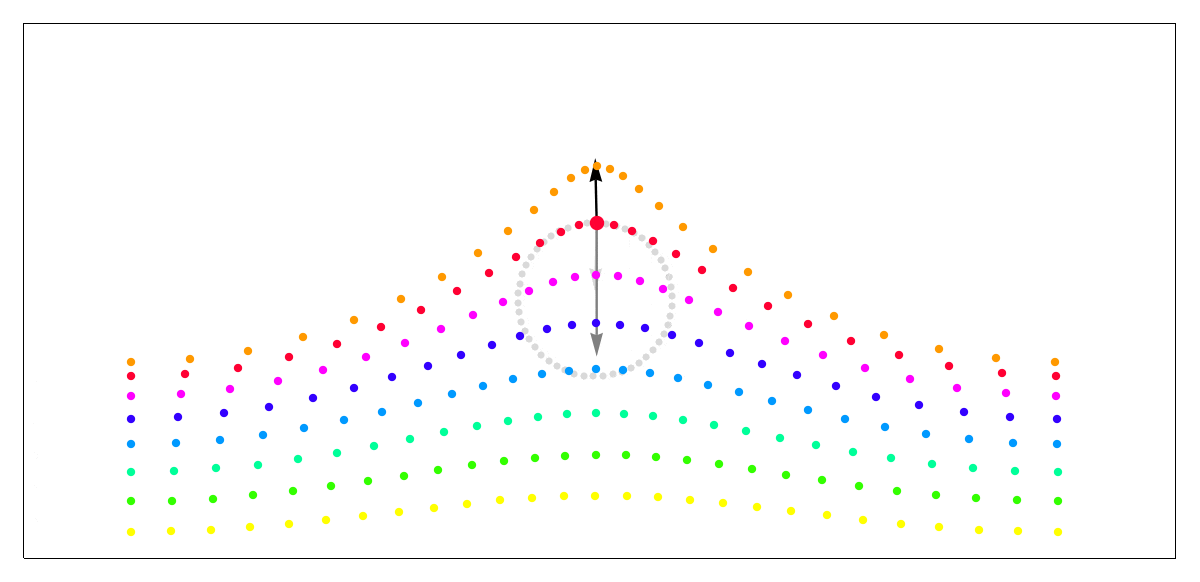
画像引用: https://en.wikipedia.org/wiki/Trochoidal_wave

実際、水に関しても、川のように水全体が移送されるようなケースを除いて、止まっている水で起こした単純な波では、上図のように水の粒子が波と一緒に移動しているわけではなく、その場で波を伝える働きをするだけで、前後に動いてはいるものの大きくはその場から動いていないのではないかと思います。(実際は表層に近い粒子ほど移送されてしまいそうですが)

具体例として「波プール」で動画検索してみると、波が発生するプールでたくさんの人が浮き輪で浮かんでいる動画を見つけられると思います。浮き輪で浮かぶ人たちは多少動きはしますが、基本的にはその場で上下したりするだけです。波の方向に沿って揺り戻しのような動きもあり、まさに上図のような動きをしていると思います。

他にも波といえば「人間ビックウェーブ」がありますね。動画検索してみると、その場で人が立ったり座ったりするだけで波を作っている動画も見つけられると思います。まさに上図の波です。ただし、人間ビックウェーブでは各点の動きが上下だけで密度に差がでませんので、少しなだらかな波になりますね。各点が上図のように横の移動も含む、つまり円運動をしていると密度差が生まれ、勾配が発生します。そうなるとちょっと本物の波っぽさが増しますね。 (人間ビックウェーブも立ったり座ったりではなく、チューチュートレインをすればよりよい波になれるかもしれません)

このように通常のSin波に各点でさらに回転運動をいれることで密度差を作るようにしたのが Gerstner Waves です！「なるほど！」という感じがします。すごいですよね。

3.2. 数式を読み解く

数式をそのままコードに落とし込めば実装は簡単にできますが、どういう意味の式なのか探っていきたいと思います。

3.2.1. 数式

GPU GemsでGerstner Wavesの数式を確認できます。以下のようになっています。

$$\bold{P}(x,y,t) = \begin{pmatrix} x + \sum{( Q_{i} A_{i} \times \bold{D}_{i}.x \times \cos(w_{i}\bold{D}_{i} \cdot (x,y) + \varphi_{i}t) )} \\ y + \sum{( Q_{i} A_{i} \times \bold{D}_{i}.y \times \cos(w_{i}\bold{D}_{i} \cdot (x,y) + \varphi_{i}t) )} \\ \sum{(A_{i} \sin(w_{i} \bold{D}_{i} \cdot (x,y) + \varphi_{i}t))} \end{pmatrix} \tag{Equation 9}$$

中身は追々見ていくとしましょう。まずこの式は $\bold{P}(x,y,t)$ という関数として表現され、$x, y, t$ の3変数によって、3次元ベクトルの値が1つ決まる数式となっています。

Gerstner Wavesでは、下図のように各点(粒子)に着目して動きを考えます。

画像引用: https://en.wikipedia.org/wiki/Trochoidal_wave

上図は断面図ですが、各点は水平な平面であれば座標 $(x,y)$ で表されます。そして時間経過$t$による変化を考えます。これらが$\bold{P}(x,y,t)$の3変数となります。そしてその値は高さも加わった立体空間の座標 $\bold{P}(x,y,t) = (x',y',z')$ となります。

3.2.2. 数式を分解してみる

それでは中身を見ていきます。

$$\bold{P}(x,y,t) = \begin{pmatrix} x + \sum{( Q_{i} A_{i} \times \bold{D}_{i}.x \times \cos(w_{i}\bold{D}_{i} \cdot (x,y) + \varphi_{i}t) )} \\ y + \sum{( Q_{i} A_{i} \times \bold{D}_{i}.y \times \cos(w_{i}\bold{D}_{i} \cdot (x,y) + \varphi_{i}t) )} \\ \sum{(A_{i} \sin(w_{i} \bold{D}_{i} \cdot (x,y) + \varphi_{i}t))} \end{pmatrix}$$

複雑そうに見えますね...。まずは各変数について記述があるので抑えます。

• $x, y$ : 座標
• $t$ : 時間
• $i$ : $\sum$ の $i$番目の項
• $Q$ : 険しさ調整値 ( parameter that controls the stepness )
• $A$ : 振幅 ( Amplitude )
• $D$ : 方向 ( Direction )
• $w$ : 周波数 ( frequency )
• $\varphi$ : 位相定数、速度 ( speed as phase-constant )

次に、単純化して見てみます。

$$\begin{aligned} \bold{P}(x,y,t) &= \begin{pmatrix} x + \sum{( Q_{i} A_{i} \times \bold{D}_{i}.x \times \cos(w_{i}\bold{D}_{i} \cdot (x,y) + \varphi_{i}t) )} \\ y + \sum{( Q_{i} A_{i} \times \bold{D}_{i}.y \times \cos(w_{i}\bold{D}_{i} \cdot (x,y) + \varphi_{i}t) )} \\ \sum{(A_{i} \sin(w_{i} \bold{D}_{i} \cdot (x,y) + \varphi_{i}t))} \end{pmatrix} \\ &= \begin{pmatrix} x + \cos の和 \\ y + \cos の和 \\ \sin の和 \end{pmatrix}\\ &= \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} + \begin{pmatrix} \cos の和 = x軸のズレ \\ \cos の和 = y軸のズレ \\ \sin の和 = z軸のズレ \end{pmatrix} \\ &= 元の座標 + ズレ \end{aligned}$$

だいぶ抵抗感がなくなったのではないでしょうか。先ほどのGif画像のように、このxy軸の$\cos$による円運動のズレによって密度差が生まれて勾配ができます。

それではまずは x軸のズレ だけを見てみましょう。

$$\sum{( Q_{i} A_{i} \times \bold{D}_{i}.x \times \cos(w_{i}\bold{D}_{i} \cdot (x,y) + \varphi_{i}t) )}$$

これも単純化しましょう。 $\cos$ の中は何かいろいろありますがどうせ出力はCos波です。時間によって位相がずれたり、周期とかが変わるだけです。そして$Q$ と $A$ と $\bold{D}_{i}.x$ がありますが、単に$\cos$に掛け算されているだけです。ならばCos波の高さに影響するだけでしょう。よって以下のような式になります。

$$\sum{( 振幅 \times \cos )}$$

つまりはただCos波の合成になっています。繰り返しになりますが、この$\cos$自体はGif画像の点の円運動を表しています。

$\sum$ で複数の $\cos$ の和になっていますが、前述の通り「複数の波」を合成しています。$i=波の数$となっています。

3.2.3. 単一の波に着目

では、 単純化するために $i=1$ でこれからは見ていきましょう。なお、複数の波の合成は最後に$i$の数を増やすだけで対応はできます。

式は分かりやすいように 「元の座標」と「円運動で表現されるズレ」の和 の形に変形しておきます。

$$\bold{P}(x,y,t) = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} + \begin{pmatrix} Q A \times \bold{D}.x \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ Q A \times \bold{D}.y \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ A \sin(w \bold{D} \cdot (x,y) + \varphi t) \end{pmatrix}$$

3.2.4. ズレ

それでは改めて x軸のズレ を見ていきたいと思います。

$$Q A \times \bold{D}.x \times \cos(w\bold{D} \cdot (x,y) + \varphi t)$$

この$\cos$は波全体の波形を表しているのではなく、ある地点$(x,y)$の点のズレを表しているということでしたね。イメージしやすいように何度も再掲しますが、以下の図の円運動している点を表しています。

画像引用: https://en.wikipedia.org/wiki/Trochoidal_wave

x軸のズレの式を大雑把にみると $振幅 \times \cos(角度)$ です。仮にx軸の振幅だけ0にしてみると上図の「x軸の横ズレ」だけがなくなります。z軸のズレがそのままであれば「z軸の縦ズレ」だけ発生するため、ただの上下移動だけとなります。そうなると全体はただのSin波になります。なお、上図を例にしているのでy軸の話は無視してます。x軸もz軸も振幅0にすれば上図の円運動(x軸とy軸の値の反復変動)は消え、ズレは発生せずに $\bold{P}(x,y,t)=(x,y,0)+(0,0,0)$となり、そもそも移動しません。

ズレの大きさである振幅が大きければより疎な部分と密な部分が顕著になり、勾配のある尖った波となります。振幅部分がどう影響するのかイメージできた気がします。ここまでは図示されていれば分かりやすいですね。

続いて、$cos$の中身について見てみます。

$$\cos(w\bold{D} \cdot (x,y) + \varphi t)$$

$w\bold{D} \cdot (x,y)$と$\varphi t$の2項があります。第1項は「周波数$w$」と「方向$\bold{D}$」と「元の座標$(x,y)$」でいずれも変化しない定数なので、項の値も定数になります。第2項は「速度」と「時間」で時間経過で速度だけ位相がずれていく値となっています。第2項によって決まった速度で位相がずれて波の動きを表しているので、分かりやすくするために第2項を削除してしまえば、止まっている波形を観測できることになります。式を分かりやすくするために消しておきましょう。

$$\cos(w\bold{D} \cdot (x,y))$$

次に$w$について見ていきます。(参考文献にて、$w$について不明瞭な箇所があり、その点について考察するので少し話が脱線します)

Wavelength (L): the crest-to-crest distance between waves in world space. Wavelength L relates to frequency w as w = 2/L.

波長 (L): ワールド空間での波の山から山の距離。波長Lは周波数wと関連があり、w=2/Lで表される。

と、書いてありますが、「波長の逆数に2が掛けられた値」とは...。周波数の公式を調べてみてもちょっとよく分かりませんでした。「1波長あたりの何かの値」を表す物理量を探してみたところ、周波数$f=\frac{v}{L}$と角波数$k=\frac{2\pi}{L}$がありました。このどちらかかなーと思ったのですが、frequencyとあるので周波数でしょうか。理解できていない式をそのまま使うことはできないので、記事の式が間違っているという前提で、$w$は周波数か角波数であると予想を立てて進めたいと思います。単に私の勘違いの可能性は多分にあるため、申し訳ないですが気づいた方は教えていただければと思います。

まずは周波数についてです。$\cos$の引数に渡すのはラジアンで、円を考えた時の角度を表すような値であり、円一周で$2\pi$でした。周波数は「1秒間の振動数」で単位は[Hz=cycle/sec]です。よって、周波数に時間[sec]をかければ、物理量はcycleとなり、1cycleのラジアンに相当する$2\pi$をかければラジアンになりそうです。

続いて角波数は「1波長分の波を1個と数えたとき、単位長さ当たりの波の個数を2π倍したもの」だそうです。単位は[radian/meter]となっており、距離[meter]をかければ物理量はラジアンになりそうです。

「$w$という値がどう扱われているのか」から、どういう物理量なのかを考え、周波数なのか角波数なのか考えます。見ていた式は$\cos(w\bold{D} \cdot (x,y))$でした。$w$に$\bold{D} \cdot (x,y)$をかけています。方向ベクトル$\bold{D}$と座標ベクトル$(x,y)$の内積なので距離ですね。よって$w$に距離をかけて$\cos$の引数としていることが分かります。このことから物理量は[radian/meter]ではないかと予想されます。単位だけをみれば角波数が候補になりました。

単位だけを見て、角波数であると断言はできませんし、そもそも間違いであると仮定した式 $w=\frac{2}{L}$から似た式を私が勝手に予想して「周波数」か「角波数」と考えているだけですので間違っているかもしれません。ただ、ここでは角波数は$w=\frac{2\pi}{L}$であるとして話を進めます。式の意味を考えてみても、位置に応じた$\cos$の値が欲しいので、角波数ではないかと思います。

なお、他にGerstnerWavesについて調べてみたところ、以下のサイトでは角波数を使っていそうでした。
https://catlikecoding.com/unity/tutorials/flow/waves/

少し長くなりましたが、$w$が単位長さ当たりの波の個数をラジアンで表すような値である「角波数」だと分かりました。$w=\frac{2\pi}{L}$で変数は$L$のみです。実際に値をいれてイメージしておきます。

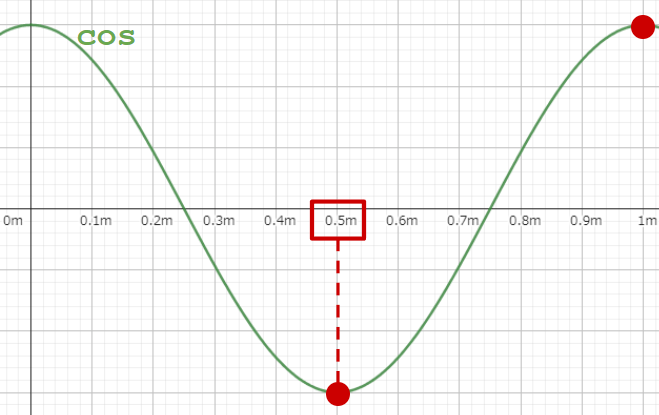
上図のような「$1m$に波1つ」という波を考えます。$L=1m$となり、$w=\frac{2\pi}{1m}=2\pi$が角波数になります。これに距離をかけるとラジアンが手に入り、「$1m$に波1つ」を表す波を観測できます。試しにこの角波数$w=2\pi$に距離$0.5m$をかければ、$\pi$が手に入ります。$\cos(\pi)=-1$であり、上図を見てもそうなっています。よって、「xyz軸の直交座標系での波を考えるとき」に、距離からその波に関して計算できる角波数は計算がしやすそうですね。

この辺りでだいぶ式の意味が見えてきた気がしますね...!!

$$\cos(w\bold{D} \cdot (x,y))$$

このうち距離を表すのが$\bold{D} \cdot (x,y)$ということでした。方向ベクトル$D$は長さ(ノルム)が1です。それとの内積を取るということは$D$に$(x,y)$を射影した「距離」を得ることになります。具体例としてx軸方向に進む波$D = (1, 0)$を考えてみます。

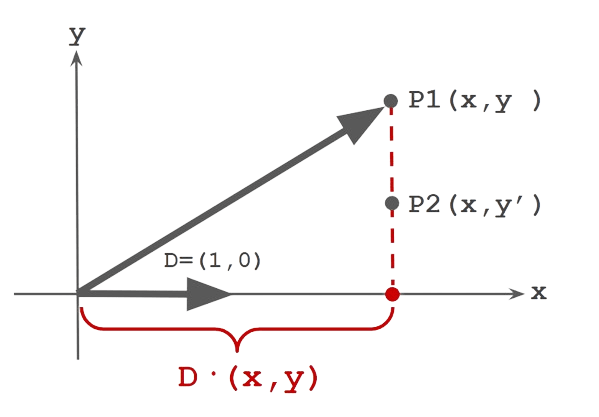
波の方向$D$と垂直に並ぶ座標(P1とP2)においては内積(射影した距離)は同じになります。2次元平面を方向ベクトルに沿った1次元直線に次元を落として、その直線における距離だけを見ることができます。それにより、平面波で位相が同じ場所で共通の距離を計算することができます。角波数にその距離をかければ、その位置の平面波のラジアンが計算できます。内積は便利ですね。

$\cos(2\pi\bold{(1,0)} \cdot (x,y))$を図示してみます。

よって、x軸のズレとは「方向ベクトル$D$に沿った距離(=平面波の位相)によって変わる$\cos$の値」となります。以下にズレをxz軸で平面波の断面を図示してみました。各点での「距離に応じた$\cos$の値」だけx軸方向にずらした図です。図のx軸の値はラジアンに変換済みです。

$L=1$とし、赤円の半径を$R$とします。

距離が0の時、ラジアンは$\frac{2\pi}{1m} 0 = 0$になります。よって$R\cos(0) = R\cdot1$です。図を見ても0の時は$R$だけx軸方向にズレています。

距離が0.25の時、ラジアンは$\frac{2\pi}{1m} 0.25 = \frac{\pi}{2}$になります。よって$R\cos(\frac{\pi}{2}) = R\cdot0 = 0$です。図を見ると$\frac{\pi}{2}$の時はズレはありません。

このように平面波の位相によって$\cos$だけズレることで、山近辺の密度が高くなり、谷近辺の密度が低くなっています。なお、仮に$R$が$0$であればズレはなくなり、ただのSin波になります。

以上がx軸のズレになります。簡単のためx軸だけ見ましたが、xy平面に関してなので方向によっては平面的にズレます。なのでxyに関してはほぼ同じです。

$$\bold{P}(x,y,t) = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} + \begin{pmatrix} Q A \times \bold{D}.x \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ Q A \times \bold{D}.y \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ A \sin(w \bold{D} \cdot (x,y) + \varphi t) \end{pmatrix}$$

改めて式を見るとxy軸にだけ$Q$が掛かっています。平面方向のズレだけを変更するパラメータであることが分かります。$Q=0$とすれば、xy軸のズレだけが消えます。z軸は元の振幅$A$で動くのでただのSin波となります。

一応、z軸のズレの式についても見ておきます。$\sin$の引数である「距離に応じた位相」はxy軸と同じ$w D \cdot (x,y) + \varphi t$ですね。単にSin波を基礎の波にしているだけです。なお、山付近の密度が高くなるようにするには、Sin波である必要があります。Cos波だと位相がずれて谷付近で密度が高くなってしまうと思います。z軸が$\sin$になっているのはおそらくそのためだと思います。

3.2.5. 波の険しさパラメータ

最後に山のとんがり具合を決めるパラメータについて説明します。

Here $Q_i$ is a parameter that controls the steepness of the waves. For a single wave $i$, $Q_i$ of $0$ gives the usual rolling sine wave, and $Q_i = 1/(w_i A_i)$ gives a sharp crest. Larger values of $Q_i$ should be avoided, because they will cause loops to form above the wave crests. In fact, we can leave the specification of $Q$ as a "steepness" parameter for the production artist, allowing a range of $0$ to $1$ , and using $Q_i = Q/(w_i A_i x\, \text{numWaves})$ to vary from totally smooth waves to the sharpest waves we can produce.

ここで$Q_i$は波の険しさを制御するパラメータである。単一の波$i$に対して、$Q_i$が$0$だと通常のSin波になり、$Q_i = 1/(w_i A_i)$だと尖った波頭となる。大きな$Q_i$は避けるべきである。なぜなら、波頭の上にループが形成されるためである。制作アーティストのための$Q$を"険しさ"のパラメータとして残し、$0$から$1$の範囲での調整を許す。実際に$Q_i = Q/(w_i A_i x\, \text{numWaves})$を使うことで、完全に滑らかな波から最も尖った波まで生成することができる。

先ほど少し触れましたが、$Q$は平面方向(xy軸)のズレの大きさの調整値のようです。

式を再掲します。

$$\bold{P}(x,y,t) = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} + \begin{pmatrix} Q A \times \bold{D}.x \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ Q A \times \bold{D}.y \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ A \sin(w \bold{D} \cdot (x,y) + \varphi t) \end{pmatrix}$$

このようにxy軸のズレの振幅の倍率として使う値のようですね。ズレの$\cos$の振幅を極端に大きくした様子を図示してみました。言われている通りにループができてしまいました。大きければ山近辺の密度が高くなり、大きすぎればループしてしまうことが分かるかと思います。このループはアーティストなどが波を作る際にパラメータ調整することで回避するようです。

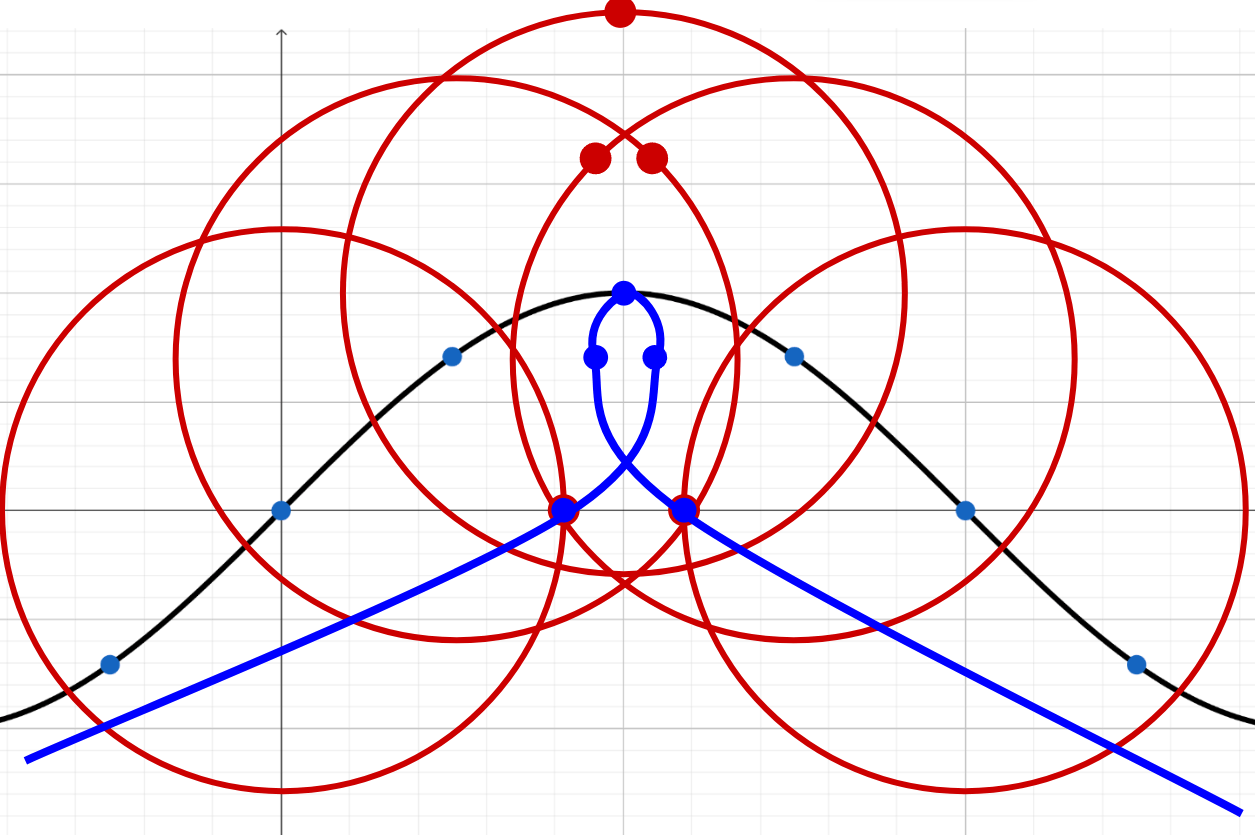
3.2.6. 合成

$\sum$となっている部分で波の数だけ足し算するだけです。

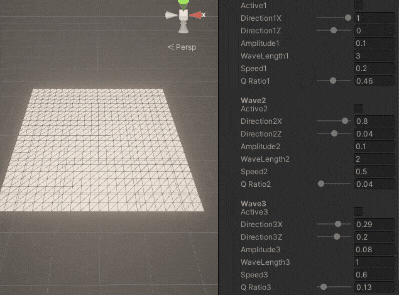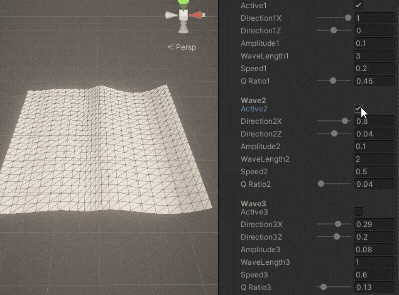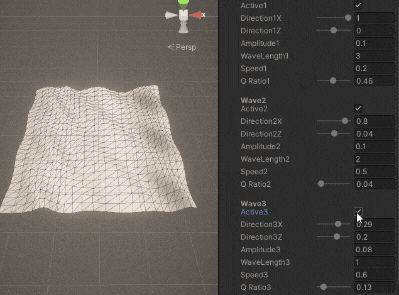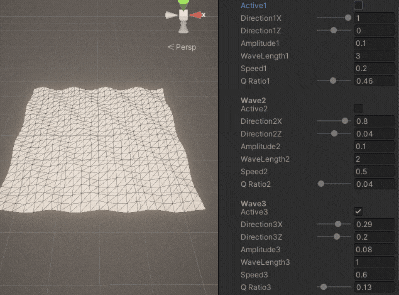
3.3. 法線の計算

ここまでで頂点座標の変換しか触れてきていませんが、頂点座標が変化しているので法線が変化しています。そのため元の法線は使えないので再計算しなくてはいけません。

$$\bold{B} = \begin{pmatrix} 1 - \sum{( Q_{i} \times \bold{D}_{i}.x^{2} \times WA \times \sin\theta )} \\ - \sum{( Q_{i} \times \bold{D}_{i}.x \times \bold{D}_{i}.y \times WA \times \sin\theta )} \\ \sum{( \bold{D}_{i}.x \times WA \times \cos\theta )} \end{pmatrix} \tag{Equation 10}$$

$$\bold{T} = \begin{pmatrix} - \sum{( Q_{i} \times D_{i}.x \times D_{i}.y \times WA \times \sin\theta )} \\ 1 - \sum{( Q_{i} \times D_{i}.y^{2} \times WA \times \sin\theta )} \\ \sum{( \bold{D}_{i}.y \times WA \times \cos\theta )} \end{pmatrix} \tag{Equation 11}$$

$$\bold{N} = \begin{pmatrix} - \sum{( \bold{D}_{i}.x \times WA \times \cos\theta )} \\ - \sum{( \bold{D}_{i}.y \times WA \times \cos\theta )} \\ 1 - \sum{( Q_{i} \times WA \times \sin\theta )} \end{pmatrix} \tag{Equation 12}$$

$$\theta = w_{i} \times \bold{D}_{i} \cdot \bold{P} + \varphi t$$

こちらの式はちゃんと解読していないので今回は割愛します...!!
読み解いた際には追記しておきたいと思います。

4. 実装

実装は以下の式をそのままコーディングするだけです。

$$\bold{P}(x,y,t) = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix} + \begin{pmatrix} Q A \times \bold{D}.x \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ Q A \times \bold{D}.y \times \cos(w\bold{D} \cdot (x,y) + \varphi t) \\ A \sin(w \bold{D} \cdot (x,y) + \varphi t) \end{pmatrix}$$

float3 CalculateSumTermOfShiftPosition(const float2 xy, const half QRatio, const half A, const half2 D, const float t, const float L, const float S)
{
	const float w = 2 * PI / L;
	const float phi = S * w;
	const float Q = (1 / (w * A)) * QRatio;
	const float theta = w * dot(D, xy) + phi * t;
	return float3(
		Q * A * D.x * cos(theta),
		Q * A * D.y * cos(theta),
		A * sin(theta)
	);
}

float3 P(float2 xy, float t)
{
	return float3(xy, 0)
		+ CalculateSumTermOfShiftPosition(xy, _QRatio1, _Amplitude1, normalize(float2(_Direction1X, _Direction1Z)), t, _WaveLength1, _Speed1) * _Active1
		+ CalculateSumTermOfShiftPosition(xy, _QRatio2, _Amplitude2, normalize(float2(_Direction2X, _Direction2Z)), t, _WaveLength2, _Speed2) * _Active2
		+ CalculateSumTermOfShiftPosition(xy, _QRatio3, _Amplitude3, normalize(float2(_Direction3X, _Direction3Z)), t, _WaveLength3, _Speed3) * _Active3;
}

あとは頂点シェーダーで上記で計算した座標を使うようにするだけです。

Varyings ProcessVertex(Attributes input)
{
	float3 positionWS = TransformObjectToWorld(input.positionOS.xyz);

	// Gemsに合わせて記号は水平平面をxyとしている。実際はxz平面なので渡すのはxz。
	const float2 xy = positionWS.xz;
	const float t = _Time.y;

	Varyings output = (Varyings)0;
	output.positionWS = P(xy, t).xzy;
	output.positionCS = TransformWorldToHClip(output.positionWS);
	return output;
}

法線についても数式をそのままコーディングするだけになります。Githubにコードをアップしているのでここでは割愛します。

https://github.com/ner-develop/GerstnerWaves

5. おわりに

頂点シェーダーで波の動きを表現できるGerstner Wavesについて紹介しました。シンプルな手法でかなり波っぽい動きを作れるのは面白いですね。今回は波の動きを作成したので次はちゃんとレンダリングもやって海を作ろうかなと思います。