🎾

【検証】小腸の表面積がテニスコート１面分ってまじ？

2021/08/26に公開

ポエム

この記事は「マイスター・ギルド：夏のアドベントカレンダー2021」14日目の記事です。

こんにちは。
見た目はおじさん、中身は小学生の逆コナン、野澤です。

さっそくですが、
みなさんはお持ちですか...？小腸

私は持ってます。いい感じのを持ってます。

この小腸ですが、表面積はテニスコート１面分に相等するって聞いたことありませんか？
私は中学生だった頃に理科の授業で先生から教わりました。

先生「小腸の表面積はテニスコート１面分もあるんやでぇ（どやっ）」
私「へぇ〜！すごい！！（ほんまか？？？）」

なぜだかその時は先生にいらっとしました。

誰が言い出したんでしょうね？これ。
教科書には検証した痕跡なんてこれっぽっちもなかったです（たぶん）。
絨毛（じゅうもう）という突起物がいっぱい付いてるから表面積は大きいんだ！ってそれっぽいことは書いていた気がします。

本当かどうか気になって夜しか眠れません。（←これ使うとおじさんのはじまり）

アドカレという~~社内業務に便乗して~~恵まれた機会をいただいたので、小腸の表面積ってほんとにテニスコートほどもあるんかいな？ということを検証してやろうと思います！

何を検証するか？

検証するには、順を追う必要があります。以下の順で確認していこうかと思います。

絨毛はいったい何本あるのか？
本当にテニスコート１面分の表面積があるのか？

小腸の内部には絨毛という突起物がたくさんあるようなので、その絨毛が何本あるのかをまずは計算します。
そして、「絨毛１本あたりの表面積 $\times$ 本数」から小腸の表面積を求めます。

※以下で用いる数値データは基本的にはネットの情報を参考にしています。正確性には疑問が残りますが、大まかな検証ですので、そこはご容赦くださいませ。

テニスコート１面分の面積

テニスコート１面は縦 $23.77 \mathrm{m}$ 、横がシングルスで $8.23 \mathrm{m}$ あるそうなので、面積は $195.63 \mathrm{m^2}$ もあります。およそ畳 $120$ 枚分の広さです。結構大きいですねぇ。
ダブルスだと横は $10.97 \mathrm{m}$ もあるので面積はもっと大きくなりますが、ここは控えめにシングルスの場合で検証を進めたいと思います。

小腸モデル

小腸についてのデータをまとめていきます。
以下に示すデータと画像をもとに、検証用の小腸モデルを脳内でイメージしてください。

小腸はおよそ直径 $5\mathrm{cm}$ ( $0.05\mathrm{m}$ )の約 $5\sim 7\mathrm{m}$ ほどの長さの臓器だそうです。
存外長いですね。
検証しやすくするために、直径(D)0.05m、長さ(L) 6mの円筒と仮定します。

小腸の内壁には絨毛という突起物が無数についています。高さは $0.5 \sim 1\mathrm{mm}$ くらいあるらしいです。
高さも簡単に考えられるように、 $1\mathrm{mm}$ （ $0.001\mathrm{m}$ ）と仮定しましょう。

この絨毛の表面積を計算したいんですが、この形状だと計算しにくいので、計算しやすい円柱状モデルを仮定します。

高さは上で述べたように $0.001\mathrm{m}$ としますが、幅は調べても出てきませんでした。。
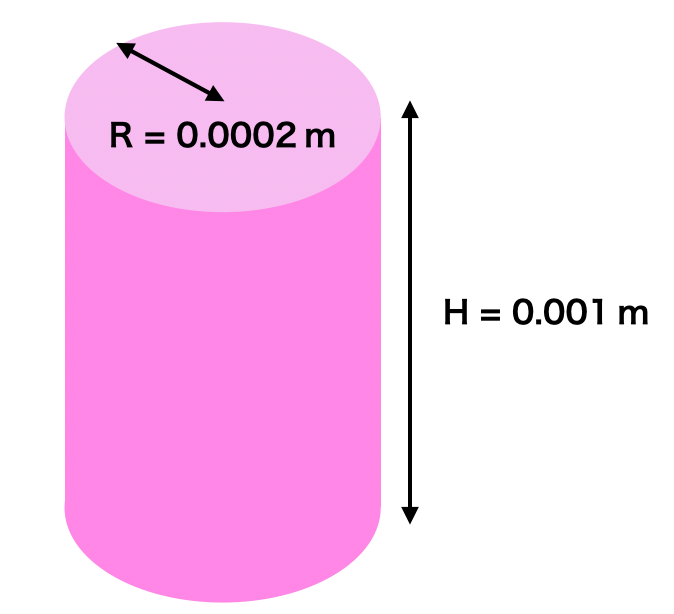
上図を見ると幅は高さの約3分の1なので、半径は $0.0002\mathrm{m}$ （高さの約6分の1）としましょう！（こういうのは思い切りが大事です）。

以上で検証に必要なデータは出揃いました。
それでは、小腸の表面積を計算していきましょう！
※計算そのものは中学数学の内容ですが、計算が苦手な方は結論だけ楽しんでくださーい。

いざ、検証

イメージを膨らませるために、小腸を切り開いた様子の図を以下に用意しました。
絨毛（円柱）がたくさん並んでいますねぇ。

真上から見たらこんな感じですかね。

Q. 絨毛はいったい何本あるのか？

絨毛（円柱）がぎっしりと並んだ場合、何本敷き詰められるかを考えると良いでしょう。

上図より、

縦には $\pi D/2R$ 個の円が並びます。

横には、 $L/2R$ 個の円が並びます。

（※個数は整数になるので、ちゃんとやるならガウス記号を用いた方がいいですが、まぁここでは大した話ではないので、割り切れると仮定します。あと、具体的な数値は最後に代入すると計算は楽です。）

よって、総数 $N$ は
$N = 縦 \times 横 = (\pi D/2R) \times (L/2R) = (\pi LD/4R^2)$ 個
となります。
$L=6\mathrm{m}, D=0.05\mathrm{m}, R=0.0002\mathrm{m}$ なので、それぞれを代入して $N$ を計算すると、、、

5,890,486個になります！ 約600万個!!

600万個の絨毛が並んでる様子を想像してみてください。
和牛の川西さんもこう言うでしょう。
「いいですねぇ。気持ち悪いですねぇ。」

Q. 本当にテニスコート１面分の表面積があるのか？

では、次に表面積を計算していきましょう。

円柱1本あたりの側面積を求めて、総数 $N$ をかけます。

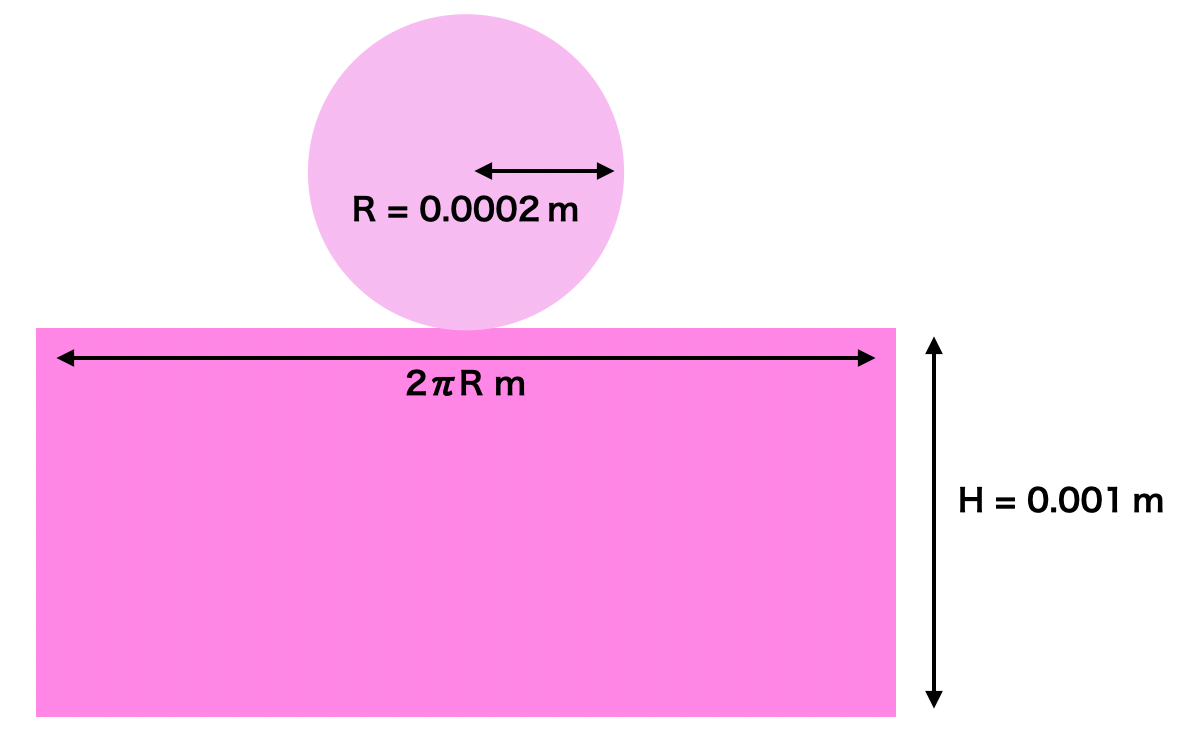
側面積は~~説明がめんどくさいので省略すると~~ $(2\pi HR + \pi R^2) \mathrm{m^2}$ です！
$H=0.001\mathrm{m}, R=0.0002\mathrm{m}$ なので、トータルの側面積は
$(2\pi \times 0.001 \times 0.0002 + \pi \times 0.0002^2) \times 5,890,486 = 8.14 \mathrm{m^2}$

あとは、円柱が敷き詰められていない部分の面積をこれに足せば完了です。下図の色のついた部分の面積を求めます。

$\pi D \times L - ( \pi R^2 \times N)= ... = 0.20 \mathrm{m^2}$

になります。

よって、ずっと気になってた小腸の表面積ですが、、、

$8.14 + 0.20 = 8.34 \mathrm{m^2}$

となります。

ここで思い出していただきたいのですが、テニスコートの面積は $195.63 \mathrm{m^2}$ なんですよ。
23倍近く違いますね。

いろんな仮定をこれまで置いてきました。
嫌がる絨毛を無理やり円柱にしたりしました。
行きずりの絨毛の長さを1mm固定にしたりもしました。
これらを例え2倍にしても、どうです？足ります？足りませんよね？？？？

おいでやす小田さんも言うと思います。

＿人人人人人人人人人人人人人人人人人人人＿
＞　全然足りてないやないかーーー！！！　＜
￣Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^YY^Y^Y￣

しかし、ここで焦るのは待ちましょう。
中身は子供の私も、ここで一旦深呼吸します。

ちょっと視点を変えてみます。
逆に、テニスコート分の表面積があると仮定した場合、絨毛はどんなサイズで、何個あればそれを実現するのか？ ということを考えてみましょう。

設問を変えてみました。大人な対応ですね。

Q. テニスコート分の表面積があると仮定した場合、絨毛はどんなサイズで、何個あればそれを実現するのか？

上では、絨毛の半径Rを $0.0002\mathrm{m}$ としましたが、一旦 $R$ という文字のままでこの設問を解いてみます。

絨毛1本あたりの側面積は上でも書いた通り、 $(2\pi HR + \pi R^2) \mathrm{m^2}$ です、

総数 $N$ は $\pi LD/4R^2$ 個。

絨毛がない部分の表面積は $\pi LD - (\pi R^2 \times N)$ 。

よって、表面積は文字だけで表現すると
$(2\pi HR + \pi R^2 ) \times (\pi LD/4R^2 ) + \pi LD - \pi R^2 \times (\pi LD/4R^2 )$
$= (\pi^2 HLD/2R) + \pi LD$

です。
次に、これが195.63となるような $R$ を求めます。

これまで同様に $H=0.001\mathrm{m}, D=0.05\mathrm{m}, L=6\mathrm{m}$ とします。

$(\pi ^2 \times 0.001 \times 6 \times 0.05/2R) + \pi \times 6 \times 0.05 = 195.63$

これを解くと、 $R = 0.0000076 \mathrm{m} = 7.6 \mu \mathrm{m}$ となります。

これは半径なので、直径では約 $15\mu \mathrm{m}$ ですね。

長ったらしい計算で疲れたかもしれませんが、ここで重要なことが明らかになりました。

絨毛がマイクロサイズなら、小腸の表面積はテニスコート1面分に到達する

ということです。

ちなみにこのときの絨毛の総数が気になる人は、 $\pi LD/4R^2$ に値を入れて電卓を叩いてみてください。そしてひだひだを感じてください。

あとでわかったこと

小腸内には絨毛だけでなく、微絨毛というマイクロサイズの突起がとてつもない数存在しているようです。→ https://ja.wikipedia.org/wiki/微絨毛

今回の検証結果は的を射たものだったと言えますね。

まとめ

検証してわかったことは以下の２つです。

mmサイズの絨毛だけでは、テニスコートの面積には達しない。（→これは結構衝撃的だった）
マイクロサイズの微絨毛という存在によってテニスコート１面分の表面積に達している。

微妙に論理の飛躍はありますが、まぁ概ね外してはいないでしょう。

さいごに

自分にとって新たな知見が得られて楽しかったです。
中学数学の知識でも、モデルの立て方でいろんな課題に取り組めますので、皆さんもぜひ興味をもったら計算計算！
こんなん、なんぼできても嬉しいですからね！