テストデータのサイズを割合ではなく、行数で求めたい。あるいは、ヘフティングの不等式の応用例。

問題の背景

機械学習におけるテストデータセットのサイズを求めたい場合、全データセット中の割合で求めることが一般的です。例えば、学習データセット：テストデータセットの割合を8:2にすることで、テストデータセットのサイズを決めるということがちょっとググるとでてきます。一方で、手元に解きたい問題のデータセットが存在せず、何らかの形で学習されたモデルだけが存在し、解きたい課題に対する精度を検証したい場合、テストデータセットを一から作ることになります。この時、どれぐらいの量のデータをアノテーションして、テストデータ作成すれば、十分なのか?という疑問が生じます。タスクに依存せずに使用できる汎用的な機械学習モデル(BERT, GPT-3など)が注目を集めている現在、以上のようなケースが実務上生じることは少なくありません。

本稿では、適切なテストデータセットのサイズの決定方法として、Hoeffding’s inequality(ヘフティングの不等式)を用いた方法を紹介致します。具体的には、以下を説明したいと思います。

• ヘフティングの不等式の意味(証明はやりません。)
• 具体例を通して、ヘフティングの不等式を用いたテストデータセットのサイズ

なお、このアイデア自体は、特に新しいものではなく、英語のブログで扱っているものがあります。

• https://www.r-bloggers.com/2021/01/what-is-a-good-test-set-size-2/#:~:text=The Decision Theory,could have used

ヘフティングの不等式

定義

$Z_i(i=1,...,n)$を互いに独立な確率変数とし、各$Z_i$が$[a, b]$の範囲の値を取るものとする。$\bar{S_n} = \frac{1}{n} \sum_1^n Z_i$とおく。任意の正の実数$t$に対して、以下の不等式が成り立つ。

$$\begin{gathered} \\\mathrm{P}\left(\left|\bar{S_n}-\mathrm{E}\left[\bar{S_n}\right]\right| \geq t\right) \leq 2 \exp \left(-\frac{2 n^2t^2}{\sum_{i=1}^n\left(b_i-a_i\right)^2}\right)\end{gathered}$$

• 証明略
  • 日本語ブログ
    • https://ludu-vorton.hatenablog.com/entry/2019/06/06/073000
  • スタンフォード、レクチャーノート
    • http://cs229.stanford.edu/extra-notes/hoeffding.pdf

解釈

$Z_i$を集めて、平均値$\bar{S_n}$を計算するということを繰り返して得られる値のリストは、$\bar{S_n}$が従うなんらかの分布$P$の実現値であると考えられます。ヘフティングの不等式は、$\bar{S_n}$とその期待値$E[\bar{S_n}]$の差が一定値$t$以上離れる確率が$t$, サンプル数$n$及び$a, b$から決まる値以下であることを表現しています。言い換えると、期待値$E[\bar{S_n}]$を$\bar{S_n}$で当てようとしたときの誤差が$t$より大きくなる確率値の上限を表現します。分布$P$で考えると以下のようになります。

上の画像を見ながら、以下を頭の中で、シミュレーションすると意味がわかると思います。斜線部は、無視できない誤差である=期待値と実現値との差分が許容範囲$t$を超えるとみなされる部分です。
$n$を大きくする → 分布が期待値を中心に尖っていって、斜線部分の面積が小さくなる。分布自体が変動して、「無視できない誤差である判定」が起こる部分が小さくなっていく。
$t$を大きくする → 許容できる範囲を広げていくことで、分布が変わらなくても、「無視できない誤差判定される部分」斜線部分が小さくなっていく。
$a$と$b$の差分が大きくなる→分散が大きくなるイメージで、分布がより平べったくなるなるので、同じ許容範囲でも、「無視できない誤差であると判定される部分」斜線部分の面積が大きくなっていく。

テストデータのサイズを決定するには？

手元には、汎用的な分類モデル$f$が存在し、このモデルが実際どの程度の性能を示すのかを正確に見積もりたいと考えています。公開されているデータセットは存在しないため、社内で評価用のデータ$X_i{(i=1,...,n)}$を作成し、テストすることで「性能の正確な見積もり」を行いたいです。今回は、テストの仕方として、インスタンスごとに、$precision(X_i, f)$を計算し、その$\bar{S_n} = \frac{1}{n}\sum presicion(X_i, f)$平均値をモデルの性能の見積もりとます。

このとき「性能が正確に見積もれている」というのは、アノテーションした有限個のテストデータセットから算出される$\bar{S_n}$がすべてのデータをアノテーションしたときに算出される期待値$E[\bar{S_n}]$に近いときであると言えます。

ここで、ヘフティングの不等式が登場します。

$$\begin{gathered} \\\mathrm{P}\left(\left|\bar{S_n}-\mathrm{E}\left[\bar{S_n}\right]\right| \geq t\right) \leq 2 \exp \left(-\frac{2 n^2t^2}{\sum_{i=1}^n\left(b_i-a_i\right)^2}\right)\end{gathered}$$

ここで、「$\bar{S_n}$が期待値$E[\bar{S_n}]$に近い」を差が$t=0.01$以内に収まることであるとするのは、実務上妥当な仮定であると言えます。また、$precision$の範囲は、$[a, b]=[0, 1]$であるため、これらを代入すると以下の式になります。

$$\begin{gathered} \\\mathrm{P}\left(\left|\bar{S_n}-\mathrm{E}\left[\bar{S_n}\right]\right| \geq 0.01\right) \leq 2 \exp \left(-{2 n(0.01)^2}\right)\end{gathered}$$

左辺が、「近くならない」確率なので、余事象の確率から、「近くなる」確率に戻して変形すると、

$$\begin{gathered} \\\mathrm{P}\left(\left|\bar{S_n}-\mathrm{E}\left[\bar{S_n}\right]\right| \leq 0.01 \right) \geq 1 - 2 \exp \left(-{2 n(0.01)^2}\right)\end{gathered}$$

右辺の値を$8000 \leq n \leq 20000$について、計算しプロットしたものが以下となります。

おおよそ、$n=18500$あたりで、右辺の値(lowwer bound)が0.95を迎えていることがわかります。このことから、大体テストデータセットを18500件作成することができれば、$precision$の平均値を誤差0.01の範囲で信頼することができると言えそうです。

$t$の範囲を広くすれば、必要なサンプル数は少なくなり、$t$の範囲を狭くすると、必要なサンプル数は増えるため、ビジネス上許容できる誤差の範囲や実際のテストデータを作るコストと相談しながら、$t$及び$n$の値を決めていく必要がありそうです。

• $t=0.05$のとき

  

  サンプル数を750件程度集めると、95%の確率で誤差0.05内の範囲に収まります。

• $t=0.001$のとき

  

  サンプル数を1.8M=1800000件程度集めると、95%の確率で誤差0.001内の範囲に収まります。

• $t=0.1$のとき

  

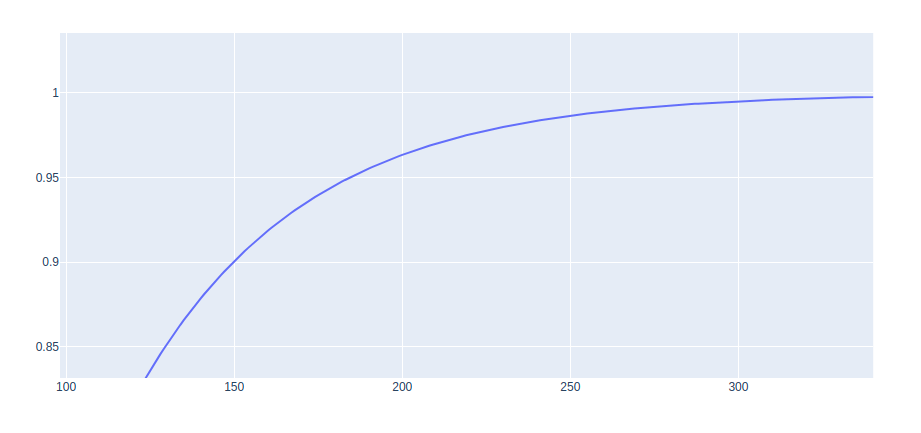
  $n=380$のときlowwer boundが0.999…なので、サンプル数を380件集められれば、新しいデータに対して、推定した$precision$が0.1ずれるということはなさそうです。