数分割問題を解くアルゴリズムを理解する
英語版 wiki にまとめてあるので読む
メモ
- 分割問題:ある集合を、総和が等しくなる集合 S1 と S2 に分けるにできるかどうかを判定する問題 (NP 完全
- 分割問題は、多項式時間の動的計画法で解くことができ、これ以外にも多くのヒューリスティックな解法が提案されている (NP 完全な問題な中でも比較的やさしいものらしい
- 分割問題の最適化:ある集合を、総和の差がなるべく小さくなる集合 S1 と S2 に分ける問題 (NP 困難
- 分割問題の最適化は、NP 困難ではあるが効率的に解く方法が見つかっている
数分割問題は総和の差が最小になるような二つの集合への分割を見つける、という最適化問題バージョンを考えることも可能です。
n≥2 の場合も含むより一般的な数分割問題はMultiway number partitioningと呼ばれます
ということで、今回ほしいのは Multiway number partitioning の solver なので、どうやってこれを解くのか調べていく。
貪欲法 (Greedy Algorithm)
簡単にいうと、集合から値を取り出した値を k 個用意した部分集合の総和の小さいところに割り当てる方法。Greedy Algorithm を拡張した Complete Greedy Algorithm と呼ばれる手法が実際には使われている。この手法は、データを降順にソートして k 分木を構築し、それぞれの枝を部分集合とする。
CGA is easily extended to partitioning into k subsets. Instead of a binary tree, we search a k-ary tree, where at each branch the corresponding number is assigned to one of the k subsets.
差分法 (Karmarkar-Karp)
一般的によく使われている手法。どういうアルゴリズムは以下の Zenn の記事がわかりやすい。
Zenn で引用されている 「Computing science: The easiest hard problem」のサイトにある図もわかりやすかった。
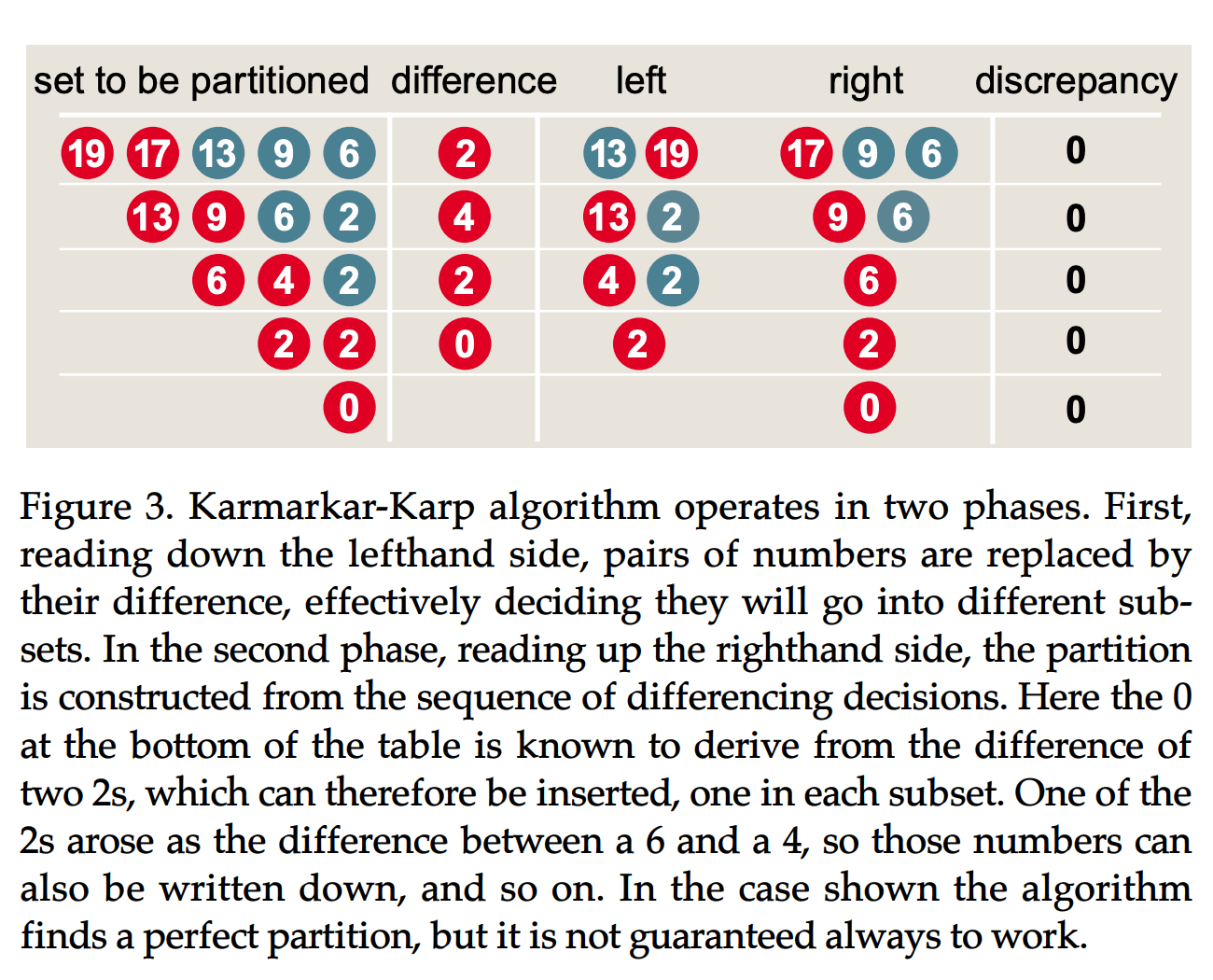
分割個数を2より大きくする場合もこのアルゴリズムが使うことができ、次のようなアルゴリズムである。
- 1つ目の要素にデータを1つずつ追加した3つの要素を持つ tuple を用意する。
例) S = {8,7,6,5,4} and k=3, then the initial partitions are ({8},{},{}), ({7},{},{}), ({6},{},{}), ({5},{},{}), ({4},{},{}). - 最大部分集合の和と最小部分集合の和の差が最も大きい2つの tuple A, B を選択する
例) 初期状態は残りの部分集合が 0 なので、大きい ({8},{},{}), ({7},{},{}) が選択される - その後、これらを「サイズが逆順」になるように結合します。具体的には、A の最小の部分集合を B の最大の部分集合と、A の2番目に小さい部分集合を B の2番目に大きい部分集合と結合します。
例) A からは {}, {} を取り出し、B からは {7}, {} を取り出し、それぞれ結合すると ({8}, {7}, {}) となる - 2,3 を繰り返す
JS の実装だと以下が参考になりそう
Multifit algorithm
数分割問題は、ビンパッキング問題と似たような問題であることに着目して解く方法。後述の通り差分法が平均的によいのと、アルゴリズムが難しかったのであまり深追いしない。
どれが一番良いのか?
最悪のケースでは、貪欲法も差分法も変わらない。multifit 法はわずかに差分法よりよい。ただ、平均的には差分法が良い解を導出する。貪欲法と比較すると常に、multifit 法と比較すると n が大きい時に常に良い解を導出する。
LDM always performs better (i.e., produces a partition with a smaller largest sum) than greedy number partitioning. It performs better than the multifit algorithm when the number of items n is sufficiently large.